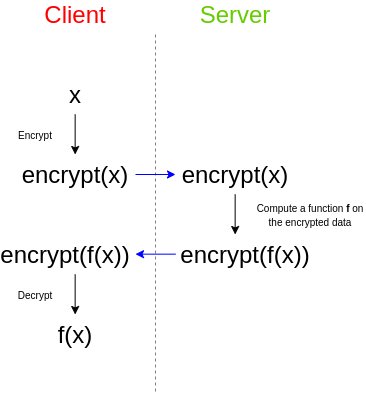
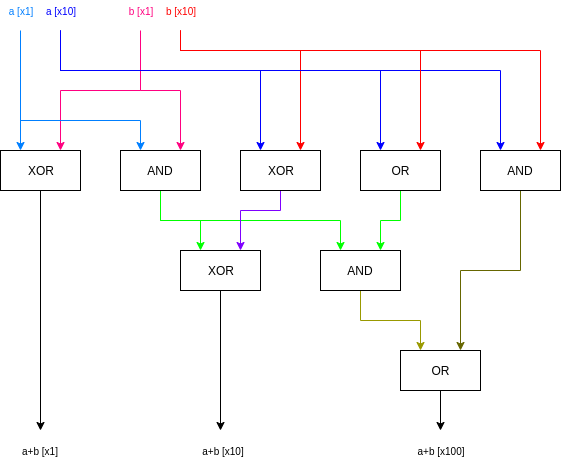
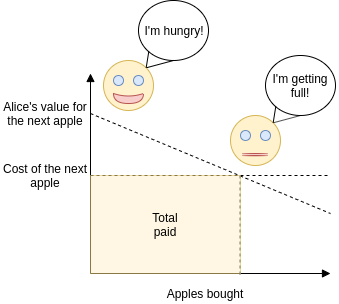
找到
227
篇与
科普知识
相关的结果
-
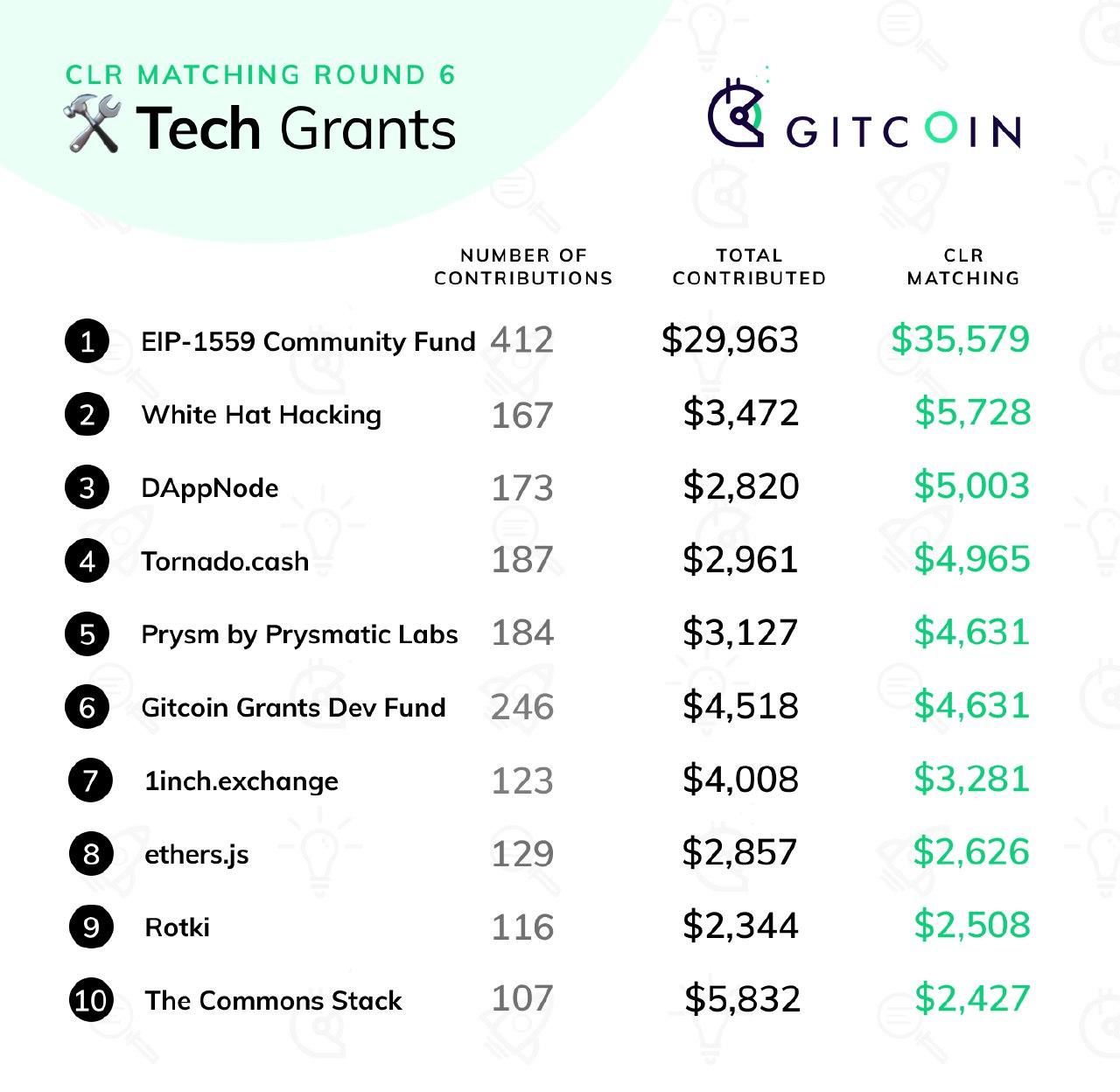
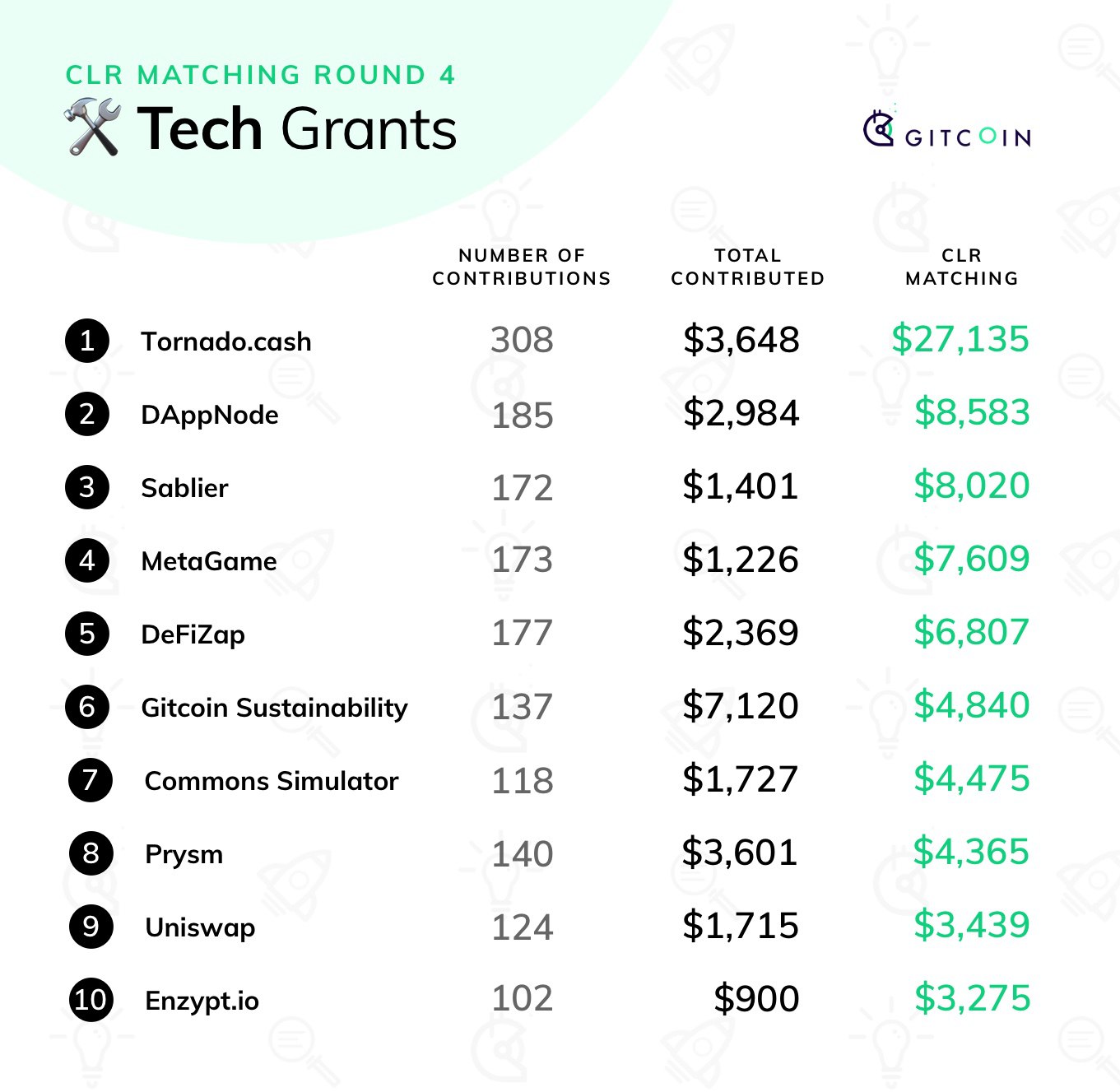
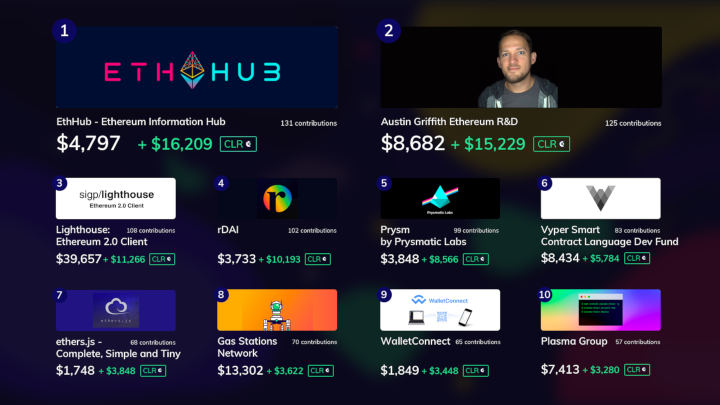
 Gitcoin Grants Round 6 Retrospective Gitcoin Grants Round 6 Retrospective2020 Jul 22 See all posts Gitcoin Grants Round 6 Retrospective Round 6 of Gitcoin Grants has just finished, with $227,847 in contributions from 1,526 contributors and $175,000 in matched funds distributed across 695 projects. This time around, we had three categories: the two usual categories of "tech" and "community" (the latter renamed from "media" to reflect a desire for a broad emphasis), and the round-6-special category Crypto For Black Lives.First of all, here are the results, starting with the tech and community sections: Stability of incomeIn the last round, one concern I raised was stability of income. People trying to earn a livelihood off of quadratic funding grants would want to have some guarantee that their income isn't going to completely disappear in the next round just because the hive mind suddenly gets excited about something else.Round 6 had two mechanisms to try to provide more stability of income:A "shopping cart" interface for giving many contributions, with an explicit "repeat your contributions from the last round" feature A rule that the matching amounts are calculated using not just contributions from this round, but also "carrying over" 1/3 of the contributions from the previous round (ie. if you made a $10 grant in the previous round, the matching formula would pretend you made a $10 grant in the previous round and also a $3.33 grant this round) was clearly successful at one goal: increasing the total number of contributions. But its effect in ensuring stability of income is hard to measure. The effect of (2), on the other hand, is easy to measure, because we have stats for the actual matching amount as well as what the matching amount "would have been" if the 1/3 carry-over rule was not in place. First from the tech category: Now from the community category: Clearly, the rule helps reduce volatility, pretty much exactly as expected. That said, one could argue that this result is trivial: you could argue that all that's going on here is something very similar to grabbing part of the revenue from round N (eg. see how the new EIP-1559 Community Fund earned less than it otherwise would have) and moving it into round N+1. Sure, numerically speaking the revenues are more "stable", but individual projects could have just provided this stability to themselves by only spending 2/3 of the pot from each round, and using the remaining third later when some future round is unexpectedly low. Why should the quadratic funding mechanism significantly increase its complexity just to achieve a gain in stability that projects could simply provide for themselves?My instinct says that it would be best to try the next round with the "repeat last round" feature but without the 1/3 carryover, and see what happens. Particularly, note that the numbers seem to show that the media section would have been "stable enough" even without the carryover. The tech section was more volatile, but only because of the sudden entrance of the EIP 1559 community fund; it would be part of the experiment to see just how common that kind of situation is.About that EIP 1559 Community fund...The big unexpected winner of this round was the EIP 1559 community fund. EIP 1559 (EIP here, FAQ here, original paper here) is a major fee market reform proposal which far-reaching consequences; it aims to improve the user experience of sending Ethereum transactions, reduce economic inefficiencies, provide an accurate in-protocol gas price oracle and burn a portion of fee revenue.Many people in the Ethereum community are very excited about this proposal, though so far there has been fairly little funding toward getting it implemented. This gitcoin grant was a large community effort toward fixing this.The grant had quite a few very large contributions, including roughly $2,400 each from myself and Eric Conner, early on. Early in the round, one could clearly see the EIP 1559 community grant having an abnormally low ratio of matched funds to contributed funds; it was somewhere around $4k matched to $20k contributed. This was because while the amount contributed was large, it came from relatively few wealthier donors, and so the matching amount was less than it would have been had the same quantity of funds come from more diverse sources - the quadratic funding formula working as intended. However, a social media push advertising the grant then led to a large number of smaller contributors following along, which then quickly raised the match to its currently very high value ($35,578).Quadratic signalingUnexpectedly, this grant proved to have a double function. First, it provided $65,473 of much-needed funding to EIP 1559 implementation. Second, it served as a credible community signal of the level of demand for the proposal. The Ethereum community has long been struggling to find effective ways to determine what "the community" supports, especially in cases of controversy.Coin votes have been used in the past, and have the advantage that they come with an answer to the key problem of determining who is a "real community member" - the answer is, your membership in the Ethereum community is proportional to how much ETH you have. However, they are plutocratic; in the famous DAO coin vote, a single "yes" voter voted with more ETH than all "no" voters put together (~20% of the total). The alternative, looking at github, reddit and twitter comments and votes to measure sentiment (sometimes derided as "proof of social media") is egalitarian, but it is easily exploitable, comes with no skin-in-the-game, and frequently falls under criticisms of "foreign interference" (are those really ethereum community members disagreeing with the proposal, or just those dastardly bitcoiners coming in from across the pond to stir up trouble?).Quadratic funding falls perfectly in the middle: the need to contribute monetary value to vote ensures that the votes of those who really care about the project count more than the votes of less-concerned outsiders, and the square-root function ensures that the votes of individual ultra-wealthy "whales" cannot beat out a poorer, but broader, coalition. A diagram from my post on quadratic payments showing how quadratic payments is "in the middle" between the extremes of voting-like systems and money-like systems, and avoids the worst flaws of both.This raises the question: might it make sense to try to use explicit quadratic voting (with the ability to vote "yes" or "no" to a proposal) as an additional signaling tool to determine community sentiment for ethereum protocol proposals?How well are "guest categories" working?Since round 5, Gitcoin Grants has had three categories per round: tech, community (called "media" before), and some "guest" category that appears only during that specific round. In round 5 this was COVID relief; in round 6, it's Crypto For Black Lives. By far the largest recipient was Black Girls CODE, claiming over 80% of the matching pot. My guess for why this happened is simple: Black Girls CODE is an established project that has been participating in the grants for several rounds already, whereas the other projects were new entrants that few people in the Ethereum community knew well. In addition, of course, the Ethereum community "understands" the value of helping people code more than it understands chambers of commerce and bail funds.This raises the question: is Gitcoin's current approach of having a guest category each round actually working well? The case for "no" is basically this: while the individual causes (empowering black communities, and fighting covid) are certainly admirable, the Ethereum community is by and large not experts at these topics, and we're certainly not experts on those specific projects working on those challenges.If the goal is to try to bring quadratic funding to causes beyond Ethereum, the natural alternative is a separate funding round marketed specifically to those communities; https://downtownstimulus.com/ is a great example of this. If the goal is to get the Ethereum community interested in other causes, then perhaps running more than one round on each cause would work better. For example, "guest categories" could last for three rounds (~6 months), with $8,333 matching per round (and there could be two or three guest categories running simultaneously). In any case, it seems like some revision of the model makes sense.CollusionNow, the bad news. This round saw an unprecedented amount of attempted collusion and other forms of fraud. Here are a few of the most egregious examples.Blatant attempted bribery:Impersonation:Many contributions with funds clearly coming from a single address:The big question is: how much fraudulent activity can be prevented in a fully automated/technological way, without requiring detailed analysis of each and every case? If quadratic funding cannot survive such fraud without needing to resort to expensive case-by-case judgement, then regardless of its virtues in an ideal world, in reality it would not be a very good mechanism!Fortunately, there is a lot that we can do to reduce harmful collusion and fraud that we are not yet doing. Stronger identity systems is one example; in this round, Gitcoin added optional SMS verification, and it seems like the in this round the detected instances of collusion were mostly github-verified accounts and not SMS-verified accounts. In the next round, making some form of extra verification beyond a github account (whether SMS or something more decentralized, eg. BrightID) seems like a good idea. To limit bribery, MACI can help, by making it impossible for a briber to tell who actually voted for any particular project.Impersonation is not really a quadratic funding-specific challenge; this could be solved with manual verification, or if one wishes for a more decentralized solution one could try using Kleros or some similar system. One could even imagine incentivized reporting: anyone can lay down a deposit and flag a project as fraudulent, triggering an investigation; if the project turns out to be legitimate the deposit is lost but if the project turns out to be fraudulent, the challenger gets half of the funds that were sent to that project.ConclusionThe best news is the unmentioned news: many of the positive behaviors coming out of the quadratic funding rounds have stabilized. We're seeing valuable projects get funded in the tech and community categories, there has been less social media contention this round than in previous rounds, and people are getting better and better at understanding the mechanism and how to participate in it.That said, the mechanism is definitely at a scale where we are seeing the kinds of attacks and challenges that we would realistically see in a larger-scale context. There are some challenges that we have not yet worked through (one that I am particularly watching out for is: matched grants going to a project that one part of the community supports and another part of the community thinks is very harmful). That said, we've gotten as far as we have with fewer problems than even I had been anticipating.I recommend holding steady, focusing on security (and scalability) for the next few rounds, and coming up with ways to increase the size of the matching pots. And I continue to look forward to seeing valuable public goods get funded!
Gitcoin Grants Round 6 Retrospective Gitcoin Grants Round 6 Retrospective2020 Jul 22 See all posts Gitcoin Grants Round 6 Retrospective Round 6 of Gitcoin Grants has just finished, with $227,847 in contributions from 1,526 contributors and $175,000 in matched funds distributed across 695 projects. This time around, we had three categories: the two usual categories of "tech" and "community" (the latter renamed from "media" to reflect a desire for a broad emphasis), and the round-6-special category Crypto For Black Lives.First of all, here are the results, starting with the tech and community sections: Stability of incomeIn the last round, one concern I raised was stability of income. People trying to earn a livelihood off of quadratic funding grants would want to have some guarantee that their income isn't going to completely disappear in the next round just because the hive mind suddenly gets excited about something else.Round 6 had two mechanisms to try to provide more stability of income:A "shopping cart" interface for giving many contributions, with an explicit "repeat your contributions from the last round" feature A rule that the matching amounts are calculated using not just contributions from this round, but also "carrying over" 1/3 of the contributions from the previous round (ie. if you made a $10 grant in the previous round, the matching formula would pretend you made a $10 grant in the previous round and also a $3.33 grant this round) was clearly successful at one goal: increasing the total number of contributions. But its effect in ensuring stability of income is hard to measure. The effect of (2), on the other hand, is easy to measure, because we have stats for the actual matching amount as well as what the matching amount "would have been" if the 1/3 carry-over rule was not in place. First from the tech category: Now from the community category: Clearly, the rule helps reduce volatility, pretty much exactly as expected. That said, one could argue that this result is trivial: you could argue that all that's going on here is something very similar to grabbing part of the revenue from round N (eg. see how the new EIP-1559 Community Fund earned less than it otherwise would have) and moving it into round N+1. Sure, numerically speaking the revenues are more "stable", but individual projects could have just provided this stability to themselves by only spending 2/3 of the pot from each round, and using the remaining third later when some future round is unexpectedly low. Why should the quadratic funding mechanism significantly increase its complexity just to achieve a gain in stability that projects could simply provide for themselves?My instinct says that it would be best to try the next round with the "repeat last round" feature but without the 1/3 carryover, and see what happens. Particularly, note that the numbers seem to show that the media section would have been "stable enough" even without the carryover. The tech section was more volatile, but only because of the sudden entrance of the EIP 1559 community fund; it would be part of the experiment to see just how common that kind of situation is.About that EIP 1559 Community fund...The big unexpected winner of this round was the EIP 1559 community fund. EIP 1559 (EIP here, FAQ here, original paper here) is a major fee market reform proposal which far-reaching consequences; it aims to improve the user experience of sending Ethereum transactions, reduce economic inefficiencies, provide an accurate in-protocol gas price oracle and burn a portion of fee revenue.Many people in the Ethereum community are very excited about this proposal, though so far there has been fairly little funding toward getting it implemented. This gitcoin grant was a large community effort toward fixing this.The grant had quite a few very large contributions, including roughly $2,400 each from myself and Eric Conner, early on. Early in the round, one could clearly see the EIP 1559 community grant having an abnormally low ratio of matched funds to contributed funds; it was somewhere around $4k matched to $20k contributed. This was because while the amount contributed was large, it came from relatively few wealthier donors, and so the matching amount was less than it would have been had the same quantity of funds come from more diverse sources - the quadratic funding formula working as intended. However, a social media push advertising the grant then led to a large number of smaller contributors following along, which then quickly raised the match to its currently very high value ($35,578).Quadratic signalingUnexpectedly, this grant proved to have a double function. First, it provided $65,473 of much-needed funding to EIP 1559 implementation. Second, it served as a credible community signal of the level of demand for the proposal. The Ethereum community has long been struggling to find effective ways to determine what "the community" supports, especially in cases of controversy.Coin votes have been used in the past, and have the advantage that they come with an answer to the key problem of determining who is a "real community member" - the answer is, your membership in the Ethereum community is proportional to how much ETH you have. However, they are plutocratic; in the famous DAO coin vote, a single "yes" voter voted with more ETH than all "no" voters put together (~20% of the total). The alternative, looking at github, reddit and twitter comments and votes to measure sentiment (sometimes derided as "proof of social media") is egalitarian, but it is easily exploitable, comes with no skin-in-the-game, and frequently falls under criticisms of "foreign interference" (are those really ethereum community members disagreeing with the proposal, or just those dastardly bitcoiners coming in from across the pond to stir up trouble?).Quadratic funding falls perfectly in the middle: the need to contribute monetary value to vote ensures that the votes of those who really care about the project count more than the votes of less-concerned outsiders, and the square-root function ensures that the votes of individual ultra-wealthy "whales" cannot beat out a poorer, but broader, coalition. A diagram from my post on quadratic payments showing how quadratic payments is "in the middle" between the extremes of voting-like systems and money-like systems, and avoids the worst flaws of both.This raises the question: might it make sense to try to use explicit quadratic voting (with the ability to vote "yes" or "no" to a proposal) as an additional signaling tool to determine community sentiment for ethereum protocol proposals?How well are "guest categories" working?Since round 5, Gitcoin Grants has had three categories per round: tech, community (called "media" before), and some "guest" category that appears only during that specific round. In round 5 this was COVID relief; in round 6, it's Crypto For Black Lives. By far the largest recipient was Black Girls CODE, claiming over 80% of the matching pot. My guess for why this happened is simple: Black Girls CODE is an established project that has been participating in the grants for several rounds already, whereas the other projects were new entrants that few people in the Ethereum community knew well. In addition, of course, the Ethereum community "understands" the value of helping people code more than it understands chambers of commerce and bail funds.This raises the question: is Gitcoin's current approach of having a guest category each round actually working well? The case for "no" is basically this: while the individual causes (empowering black communities, and fighting covid) are certainly admirable, the Ethereum community is by and large not experts at these topics, and we're certainly not experts on those specific projects working on those challenges.If the goal is to try to bring quadratic funding to causes beyond Ethereum, the natural alternative is a separate funding round marketed specifically to those communities; https://downtownstimulus.com/ is a great example of this. If the goal is to get the Ethereum community interested in other causes, then perhaps running more than one round on each cause would work better. For example, "guest categories" could last for three rounds (~6 months), with $8,333 matching per round (and there could be two or three guest categories running simultaneously). In any case, it seems like some revision of the model makes sense.CollusionNow, the bad news. This round saw an unprecedented amount of attempted collusion and other forms of fraud. Here are a few of the most egregious examples.Blatant attempted bribery:Impersonation:Many contributions with funds clearly coming from a single address:The big question is: how much fraudulent activity can be prevented in a fully automated/technological way, without requiring detailed analysis of each and every case? If quadratic funding cannot survive such fraud without needing to resort to expensive case-by-case judgement, then regardless of its virtues in an ideal world, in reality it would not be a very good mechanism!Fortunately, there is a lot that we can do to reduce harmful collusion and fraud that we are not yet doing. Stronger identity systems is one example; in this round, Gitcoin added optional SMS verification, and it seems like the in this round the detected instances of collusion were mostly github-verified accounts and not SMS-verified accounts. In the next round, making some form of extra verification beyond a github account (whether SMS or something more decentralized, eg. BrightID) seems like a good idea. To limit bribery, MACI can help, by making it impossible for a briber to tell who actually voted for any particular project.Impersonation is not really a quadratic funding-specific challenge; this could be solved with manual verification, or if one wishes for a more decentralized solution one could try using Kleros or some similar system. One could even imagine incentivized reporting: anyone can lay down a deposit and flag a project as fraudulent, triggering an investigation; if the project turns out to be legitimate the deposit is lost but if the project turns out to be fraudulent, the challenger gets half of the funds that were sent to that project.ConclusionThe best news is the unmentioned news: many of the positive behaviors coming out of the quadratic funding rounds have stabilized. We're seeing valuable projects get funded in the tech and community categories, there has been less social media contention this round than in previous rounds, and people are getting better and better at understanding the mechanism and how to participate in it.That said, the mechanism is definitely at a scale where we are seeing the kinds of attacks and challenges that we would realistically see in a larger-scale context. There are some challenges that we have not yet worked through (one that I am particularly watching out for is: matched grants going to a project that one part of the community supports and another part of the community thinks is very harmful). That said, we've gotten as far as we have with fewer problems than even I had been anticipating.I recommend holding steady, focusing on security (and scalability) for the next few rounds, and coming up with ways to increase the size of the matching pots. And I continue to look forward to seeing valuable public goods get funded! -
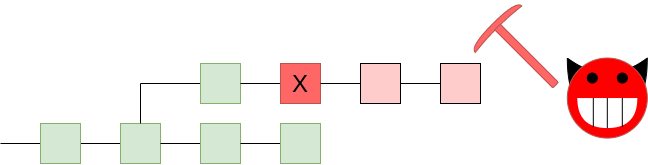
 A Philosophy of Blockchain Validation A Philosophy of Blockchain Validation2020 Aug 17 See all posts A Philosophy of Blockchain Validation See also:A Proof of Stake Design Philosophy The Meaning of Decentralization Engineering Security through Coordination Problems One of the most powerful properties of a blockchain is the fact that every single part of the blockchain's execution can be independently validated. Even if a great majority of a blockchain's miners (or validators in PoS) get taken over by an attacker, if that attacker tries to push through invalid blocks, the network will simply reject them. Even those users that were not verifying blocks at that time can be (potentially automatically) warned by those who were, at which point they can check that the attacker's chain is invalid, and automatically reject it and coordinate on accepting a chain that follows the rules.But how much validation do we actually need? Do we need a hundred independent validating nodes, a thousand? Do we need a culture where the average person in the world runs software that checks every transaction? It's these questions that are a challenge, and a very important challenge to resolve especially if we want to build blockchains with consensus mechanisms better than the single-chain "Nakamoto" proof of work that the blockchain space originally started with.Why validate? A 51% attack pushing through an invalid block. We want the network to reject the chain!There are two main reasons why it's beneficial for a user to validate the chain. First, it maximizes the chance that the node can correctly determine and say on the canonical chain - the chain that the community accepts as legitimate. Typically, the canonical chain is defined as something like "the valid chain that has the most miners/validators supporting it" (eg. the "longest valid chain" in Bitcoin). Invalid chains are rejected by definition, and if there is a choice between multiple valid chains, the chain that has the most support from miners/validators wins out. And so if you have a node that verifies all the validity conditions, and hence detects which chains are valid and which chains are not, that maximizes your chances of correctly detecting what the canonical chain actually is.But there is also another deeper reason why validating the chain is beneficial. Suppose that a powerful actor tries to push through a change to the protocol (eg. changing the issuance), and has the support of the majority of miners. If no one else validates the chain, this attack can very easily succeed: everyone's clients will, by default, accept the new chain, and by the time anyone sees what is going on, it will be up to the dissenters to try to coordinate a rejection of that chain. But if average users are validating, then the coordination problem falls on the other side: it's now the responsibility of whoever is trying to change the protocol to convince the users to actively download the software patch to accept the protocol change.If enough users are validating, then instead of defaulting to victory, a contentious attempt to force a change of the protocol will default to chaos. Defaulting to chaos still causes a lot of disruption, and would require out-of-band social coordination to resolve, but it places a much larger barrier in front of the attacker, and makes attackers much less confident that they will be able to get away with a clean victory, making them much less motivated to even try to start an attack. If most users are validating (directly or indirectly), and an attack has only the support of the majority of miners, then the attack will outright default to failure - the best outcome of all.The definition view versus the coordination viewNote that this reasoning is very different from a different line of reasoning that we often hear: that a chain that changes the rules is somehow "by definition" not the correct chain, and that no matter how many other users accept some new set of rules, what matters is that you personally can stay on the chain with the old rules that you favor.Here is one example of the "by definition" perspective from Gavin Andresen:Here's another from the Wasabi wallet; this one comes even more directly from the perspective of explaining why full nodes are valuable:Notice two core components of this view:A version of the chain that does not accept the rules that you consider fundamental and non-negotiable is by definition not bitcoin (or not ethereum or whatever other chain), not matter how many other people accept that chain. What matters is that you remain on a chain that has rules that you consider acceptable. However, I believe this "individualist" view to be very wrong. To see why, let us take a look at the scenario that we are worried about: the vast majority of participants accept some change to protocol rules that you find unacceptable. For example, imagine a future where transaction fees are very low, and to keep the chain secure, almost everyone else agrees to change to a new set of rules that increases issuance. You stubbornly keep running a node that continues to enforce the old rules, and you fork off to a different chain than the majority.From your point of view, you still have your coins in a system that runs on rules that you accept. But so what? Other users will not accept your coins. Exchanges will not accept your coins. Public websites may show the price of the new coin as being some high value, but they're referring to the coins on the majority chain; your coins are valueless. Cryptocurrencies and blockchains are fundamentally social constructs; without other people believing in them, they mean nothing.So what is the alternative view? The core idea is to look at blockchains as engineering security through coordination problems.Normally, coordination problems in the world are a bad thing: while it would be better for most people if the English language got rid of its highly complex and irregular spelling system and made a phonetic one, or if the United States switched to metric, or if we could immediately drop all prices and wages by ten percent in the event of a recession, in practice this requires everyone to agree on the switch at the same time, and this is often very very hard.With blockchain applications, however, we are using coordination problems to our advantage. We are using the friction that coordination problems create as a bulwark against malfeasance by centralized actors. We can build systems that have property X, and we can guarantee that they will preserve property X because changing the rules from X to not-X would require a whole bunch of people to agree to update their software at the same time. Even if there is an actor that could force the change, doing so would be hard - much much harder than it would be if it were instead the responsibility of users to actively coordinate dissent to resist a change.Note one particular consequence of this view: it's emphatically not the case that the purpose of your full node is just to protect you, and in the case of a contentious hard fork, people with full nodes are safe and people without full nodes are vulnerable. Rather, the perspective here is much more one of herd immunity: the more people are validating, the more safe everyone is, and even if only some portion of people are validating, everyone gets a high level of protection as a result.Looking deeper into validationWe now get to the next topic, and one that is very relevant to topics such as light clients and sharding: what are we actually accomplishing by validating? To understand this, let us go back to an earlier point. If an attack happens, I would argue that we have the following preference order over how the attack goes: default to failure > default to chaos > default to victory The ">" here of course means "better than". The best is if an attack outright fails; the second best is if an attack leads to confusion, with everyone disagreeing on what the correct chain is, and the worst is if an attack succeeds. Why is chaos so much better than victory? This is a matter of incentives: chaos raises costs for the attacker, and denies them the certainty that they will even win, discouraging attacks from being attempted in the first place. A default-to-chaos environment means that an attacker needs to win both the blockchain war of making a 51% attack and the "social war" of convincing the community to follow along. This is much more difficult, and much less attractive, than just launching a 51% attack and claiming victory right there.The goal of validation is then to move away from default to victory to (ideally) default to failure or (less ideally) default to chaos. If you have a fully validating node, and an attacker tries to push through a chain with different rules, then the attack fails. If some people have a fully validating node but many others don't, the attack leads to chaos. But now we can think: are there other ways of achieving the same effect?Light clients and fraud proofsOne natural advancement in this regard is light clients with fraud proofs. Most blockchain light clients that exist today work by simply validating that the majority of miners support a particular block, and not bothering to check if the other protocol rules are being enforced. The client runs on the trust assumption that the majority of miners is honest. If a contentious fork happens, the client follows the majority chain by default, and it's up to users to take an active step if they want to follow the minority chain with the old rules; hence, today's light clients under attack default to victory. But with fraud proof technology, the situation starts to look very different.A fraud proof in its simplest form works as follows. Typically, a single block in a blockchain only touches a small portion of the blockchain "state" (account balances, smart contract code....). If a fully verifying node processes a block and finds that it is invalid, they can generate a package (the fraud proof) containing the block along with just enough data from the blockchain state to process the block. They broadcast this package to light clients. Light clients can then take the package and use that data to verify the block themselves, even if they have no other data from the chain. A single block in a blockchain touches only a few accounts. A fraud proof would contain the data in those accounts along with Merkle proofs proving that that data is correct. This technique is also sometimes known as stateless validation: instead of keeping a full database of the blockchain state, clients can keep only the block headers, and they can verify any block in real time by asking other nodes for a Merkle proof for any desired state entries that block validation is accessing.The power of this technique is that light clients can verify individual blocks only if they hear an alarm (and alarms are verifiable, so if a light client hears a false alarm, they can just stop listening to alarms from that node). Hence, under normal circumstances, the light client is still light, checking only which blocks are supported by the majority of miners/validators. But under those exceptional circumstances where the majority chain contains a block that the light client would not accept, as long as there is at least one honest node verifying the fraudulent block, that node will see that it is invalid, broadcast a fraud proof, and thereby cause the rest of the network to reject it.ShardingSharding is a natural extension of this: in a sharded system, there are too many transactions in the system for most people to be verifying directly all the time, but if the system is well designed then any individual invalid block can be detected and its invalidity proven with a fraud proof, and that proof can be broadcasted across the entire network. A sharded network can be summarized as everyone being a light client. And as long as each shard has some minimum threshold number of participants, the network has herd immunity.In addition, the fact that in a sharded system block production (and not just block verification) is highly accessible and can be done even on consumer laptops is also very important. The lack of dependence on high-performance hardware at the core of the network ensures that there is a low bar on dissenting minority chains being viable, making it even harder for a majority-driven protocol change to "win by default" and bully everyone else into submission.This is what auditability usually means in the real world: not that everyone is verifying everything all the time, but that (i) there are enough eyes on each specific piece that if there is an error it will get detected, and (ii) when an error is detected that fact that be made clear and visible to all.That said, in the long run blockchains can certainly improve on this. One particular source of improvements is ZK-SNARKs (or "validity proofs"): efficiently verifiably cryptographic proofs that allow block producers to prove to clients that blocks satisfy some arbitrarily complex validity conditions. Validity proofs are stronger than fraud proofs because they do not depend on an interactive game to catch fraud. Another important technology is data availability checks, which can protect against blocks whose data is not fully published. Data availability checks do rely on a very conservative assumption that there exists at least some small number of honest nodes somewhere in the network continues to apply, though the good news is that this minimum honesty threshold is low, and does not grow even if there is a very large number of attackers.Timing and 51% attacksNow, let us get to the most powerful consequence of the "default to chaos" mindset: 51% attacks themselves. The current norm in many communities is that if a 51% attack wins, then that 51% attack is necessarily the valid chain. This norm is often stuck to quite strictly; and a recent 51% attack on Ethereum Classic illustrated this quite well. The attacker reverted more than 3000 blocks (stealing 807,260 ETC in a double-spend in the process), which pushed the chain farther back in history than one of the two ETC clients (OpenEthereum) was technically able to revert; as a result, Geth nodes went with the attacker's chain but OpenEthereum nodes stuck with the original chain.We can say that the attack did in fact default to chaos, though this was an accident and not a deliberate design decision of the ETC community. Unfortunately, the community then elected to accept the (longer) attack chain as canonical, a move described by the eth_classic twitter as "following Proof of Work as intended". Hence, the community norms actively helped the attacker win.But we could instead agree on a definition of the canonical chain that works differently: particularly, imagine a rule that once a client has accepted a block as part of the canonical chain, and that block has more than 100 descendants, the client will from then on never accept a chain that does not include that block. Alternatively, in a finality-bearing proof of stake setup (which eg. ethereum 2.0 is), imagine a rule that once a block is finalized it can never be reverted. 5 block revert limit only for illustration purposes; in reality the limit could be something longer like 100-1000 blocks.To be clear, this introduces a significant change to how canonicalness is determined: instead of clients just looking at the data they receive by itself, clients also look at when that data was received. This introduces the possibility that, because of network latency, clients disagree: what if, because of a massive attack, two conflicting blocks A and B finalize at the same time, and some clients see A first and some see B first? But I would argue that this is good: it means that instead of defaulting to victory, even 51% attacks that just try to revert transactions default to chaos, and out-of-band emergency response can choose which of the two blocks the chain continues with. If the protocol is well-designed, forcing an escalation to out-of-band emergency response should be very expensive: in proof of stake, such a thing would require 1/3 of validators sacrificing their deposits and getting slashed.Potentially, we could expand this approach. We could try to make 51% attacks that censor transactions default to chaos too. Research on timeliness detectors pushes things further in the direction of attacks of all types defaulting to failure, though a little chaos remains because timeliness detectors cannot help nodes that are not well-connected and online.For a blockchain community that values immutability, implementing revert limits of this kind are arguably the superior path to take. It is difficult to honestly claim that a blockchain is immutable when no matter how long a transaction has been accepted in a chain, there is always the possibility that some unexpected activity by powerful actors can come along and revert it. Of course, I would claim that even BTC and ETC do already have a revert limit at the extremes; if there was an attack that reverted weeks of activity, the community would likely adopt a user-activated soft fork to reject the attackers' chain. But more definitively agreeing on and formalizing this seems like a step forward.ConclusionThere are a few "morals of the story" here. First, if we accept the legitimacy of social coordination, and we accept the legitimacy of indirect validation involving "1-of-N" trust models (that is, assuming that there exists one honest person in the network somewhere; NOT the same as assuming that one specific party, eg. Infura, is honest), then we can create blockchains that are much more scalable.Second, client-side validation is extremely important for all of this to work. A network where only a few people run nodes and everyone else really does trust them is a network that can easily be taken over by special interests. But avoiding such a fate does not require going to the opposite extreme and having everyone always validate everything! Systems that allow each individual block to be verified in isolation, so users only validate blocks if someone else raises an alarm, are totally reasonable and serve the same effect. But this requires accepting the "coordination view" of what validation is for.Third, if we allow the definition of canonicalness includes timing, then we open many doors in improving our ability to reject 51% attacks. The easiest property to gain is weak subjectivity: the idea that if clients are required to log on at least once every eg. 3 months, and refuse to revert longer than that, then we can add slashing to proof of stake and make attacks very expensive. But we can go further: we can reject chains that revert finalized blocks and thereby protect immutability, and even protect against censorship. Because the network is unpredictable, relying on timing does imply attacks "defaulting to chaos" in some cases, but the benefits are very much worth it.With all of these ideas in mind, we can avoid the traps of (i) over-centralization, (ii) overly redundant verification leading to inefficiency and (iii) misguided norms accidentally making attacks easier, and better work toward building more resilient, performant and secure blockchains.
A Philosophy of Blockchain Validation A Philosophy of Blockchain Validation2020 Aug 17 See all posts A Philosophy of Blockchain Validation See also:A Proof of Stake Design Philosophy The Meaning of Decentralization Engineering Security through Coordination Problems One of the most powerful properties of a blockchain is the fact that every single part of the blockchain's execution can be independently validated. Even if a great majority of a blockchain's miners (or validators in PoS) get taken over by an attacker, if that attacker tries to push through invalid blocks, the network will simply reject them. Even those users that were not verifying blocks at that time can be (potentially automatically) warned by those who were, at which point they can check that the attacker's chain is invalid, and automatically reject it and coordinate on accepting a chain that follows the rules.But how much validation do we actually need? Do we need a hundred independent validating nodes, a thousand? Do we need a culture where the average person in the world runs software that checks every transaction? It's these questions that are a challenge, and a very important challenge to resolve especially if we want to build blockchains with consensus mechanisms better than the single-chain "Nakamoto" proof of work that the blockchain space originally started with.Why validate? A 51% attack pushing through an invalid block. We want the network to reject the chain!There are two main reasons why it's beneficial for a user to validate the chain. First, it maximizes the chance that the node can correctly determine and say on the canonical chain - the chain that the community accepts as legitimate. Typically, the canonical chain is defined as something like "the valid chain that has the most miners/validators supporting it" (eg. the "longest valid chain" in Bitcoin). Invalid chains are rejected by definition, and if there is a choice between multiple valid chains, the chain that has the most support from miners/validators wins out. And so if you have a node that verifies all the validity conditions, and hence detects which chains are valid and which chains are not, that maximizes your chances of correctly detecting what the canonical chain actually is.But there is also another deeper reason why validating the chain is beneficial. Suppose that a powerful actor tries to push through a change to the protocol (eg. changing the issuance), and has the support of the majority of miners. If no one else validates the chain, this attack can very easily succeed: everyone's clients will, by default, accept the new chain, and by the time anyone sees what is going on, it will be up to the dissenters to try to coordinate a rejection of that chain. But if average users are validating, then the coordination problem falls on the other side: it's now the responsibility of whoever is trying to change the protocol to convince the users to actively download the software patch to accept the protocol change.If enough users are validating, then instead of defaulting to victory, a contentious attempt to force a change of the protocol will default to chaos. Defaulting to chaos still causes a lot of disruption, and would require out-of-band social coordination to resolve, but it places a much larger barrier in front of the attacker, and makes attackers much less confident that they will be able to get away with a clean victory, making them much less motivated to even try to start an attack. If most users are validating (directly or indirectly), and an attack has only the support of the majority of miners, then the attack will outright default to failure - the best outcome of all.The definition view versus the coordination viewNote that this reasoning is very different from a different line of reasoning that we often hear: that a chain that changes the rules is somehow "by definition" not the correct chain, and that no matter how many other users accept some new set of rules, what matters is that you personally can stay on the chain with the old rules that you favor.Here is one example of the "by definition" perspective from Gavin Andresen:Here's another from the Wasabi wallet; this one comes even more directly from the perspective of explaining why full nodes are valuable:Notice two core components of this view:A version of the chain that does not accept the rules that you consider fundamental and non-negotiable is by definition not bitcoin (or not ethereum or whatever other chain), not matter how many other people accept that chain. What matters is that you remain on a chain that has rules that you consider acceptable. However, I believe this "individualist" view to be very wrong. To see why, let us take a look at the scenario that we are worried about: the vast majority of participants accept some change to protocol rules that you find unacceptable. For example, imagine a future where transaction fees are very low, and to keep the chain secure, almost everyone else agrees to change to a new set of rules that increases issuance. You stubbornly keep running a node that continues to enforce the old rules, and you fork off to a different chain than the majority.From your point of view, you still have your coins in a system that runs on rules that you accept. But so what? Other users will not accept your coins. Exchanges will not accept your coins. Public websites may show the price of the new coin as being some high value, but they're referring to the coins on the majority chain; your coins are valueless. Cryptocurrencies and blockchains are fundamentally social constructs; without other people believing in them, they mean nothing.So what is the alternative view? The core idea is to look at blockchains as engineering security through coordination problems.Normally, coordination problems in the world are a bad thing: while it would be better for most people if the English language got rid of its highly complex and irregular spelling system and made a phonetic one, or if the United States switched to metric, or if we could immediately drop all prices and wages by ten percent in the event of a recession, in practice this requires everyone to agree on the switch at the same time, and this is often very very hard.With blockchain applications, however, we are using coordination problems to our advantage. We are using the friction that coordination problems create as a bulwark against malfeasance by centralized actors. We can build systems that have property X, and we can guarantee that they will preserve property X because changing the rules from X to not-X would require a whole bunch of people to agree to update their software at the same time. Even if there is an actor that could force the change, doing so would be hard - much much harder than it would be if it were instead the responsibility of users to actively coordinate dissent to resist a change.Note one particular consequence of this view: it's emphatically not the case that the purpose of your full node is just to protect you, and in the case of a contentious hard fork, people with full nodes are safe and people without full nodes are vulnerable. Rather, the perspective here is much more one of herd immunity: the more people are validating, the more safe everyone is, and even if only some portion of people are validating, everyone gets a high level of protection as a result.Looking deeper into validationWe now get to the next topic, and one that is very relevant to topics such as light clients and sharding: what are we actually accomplishing by validating? To understand this, let us go back to an earlier point. If an attack happens, I would argue that we have the following preference order over how the attack goes: default to failure > default to chaos > default to victory The ">" here of course means "better than". The best is if an attack outright fails; the second best is if an attack leads to confusion, with everyone disagreeing on what the correct chain is, and the worst is if an attack succeeds. Why is chaos so much better than victory? This is a matter of incentives: chaos raises costs for the attacker, and denies them the certainty that they will even win, discouraging attacks from being attempted in the first place. A default-to-chaos environment means that an attacker needs to win both the blockchain war of making a 51% attack and the "social war" of convincing the community to follow along. This is much more difficult, and much less attractive, than just launching a 51% attack and claiming victory right there.The goal of validation is then to move away from default to victory to (ideally) default to failure or (less ideally) default to chaos. If you have a fully validating node, and an attacker tries to push through a chain with different rules, then the attack fails. If some people have a fully validating node but many others don't, the attack leads to chaos. But now we can think: are there other ways of achieving the same effect?Light clients and fraud proofsOne natural advancement in this regard is light clients with fraud proofs. Most blockchain light clients that exist today work by simply validating that the majority of miners support a particular block, and not bothering to check if the other protocol rules are being enforced. The client runs on the trust assumption that the majority of miners is honest. If a contentious fork happens, the client follows the majority chain by default, and it's up to users to take an active step if they want to follow the minority chain with the old rules; hence, today's light clients under attack default to victory. But with fraud proof technology, the situation starts to look very different.A fraud proof in its simplest form works as follows. Typically, a single block in a blockchain only touches a small portion of the blockchain "state" (account balances, smart contract code....). If a fully verifying node processes a block and finds that it is invalid, they can generate a package (the fraud proof) containing the block along with just enough data from the blockchain state to process the block. They broadcast this package to light clients. Light clients can then take the package and use that data to verify the block themselves, even if they have no other data from the chain. A single block in a blockchain touches only a few accounts. A fraud proof would contain the data in those accounts along with Merkle proofs proving that that data is correct. This technique is also sometimes known as stateless validation: instead of keeping a full database of the blockchain state, clients can keep only the block headers, and they can verify any block in real time by asking other nodes for a Merkle proof for any desired state entries that block validation is accessing.The power of this technique is that light clients can verify individual blocks only if they hear an alarm (and alarms are verifiable, so if a light client hears a false alarm, they can just stop listening to alarms from that node). Hence, under normal circumstances, the light client is still light, checking only which blocks are supported by the majority of miners/validators. But under those exceptional circumstances where the majority chain contains a block that the light client would not accept, as long as there is at least one honest node verifying the fraudulent block, that node will see that it is invalid, broadcast a fraud proof, and thereby cause the rest of the network to reject it.ShardingSharding is a natural extension of this: in a sharded system, there are too many transactions in the system for most people to be verifying directly all the time, but if the system is well designed then any individual invalid block can be detected and its invalidity proven with a fraud proof, and that proof can be broadcasted across the entire network. A sharded network can be summarized as everyone being a light client. And as long as each shard has some minimum threshold number of participants, the network has herd immunity.In addition, the fact that in a sharded system block production (and not just block verification) is highly accessible and can be done even on consumer laptops is also very important. The lack of dependence on high-performance hardware at the core of the network ensures that there is a low bar on dissenting minority chains being viable, making it even harder for a majority-driven protocol change to "win by default" and bully everyone else into submission.This is what auditability usually means in the real world: not that everyone is verifying everything all the time, but that (i) there are enough eyes on each specific piece that if there is an error it will get detected, and (ii) when an error is detected that fact that be made clear and visible to all.That said, in the long run blockchains can certainly improve on this. One particular source of improvements is ZK-SNARKs (or "validity proofs"): efficiently verifiably cryptographic proofs that allow block producers to prove to clients that blocks satisfy some arbitrarily complex validity conditions. Validity proofs are stronger than fraud proofs because they do not depend on an interactive game to catch fraud. Another important technology is data availability checks, which can protect against blocks whose data is not fully published. Data availability checks do rely on a very conservative assumption that there exists at least some small number of honest nodes somewhere in the network continues to apply, though the good news is that this minimum honesty threshold is low, and does not grow even if there is a very large number of attackers.Timing and 51% attacksNow, let us get to the most powerful consequence of the "default to chaos" mindset: 51% attacks themselves. The current norm in many communities is that if a 51% attack wins, then that 51% attack is necessarily the valid chain. This norm is often stuck to quite strictly; and a recent 51% attack on Ethereum Classic illustrated this quite well. The attacker reverted more than 3000 blocks (stealing 807,260 ETC in a double-spend in the process), which pushed the chain farther back in history than one of the two ETC clients (OpenEthereum) was technically able to revert; as a result, Geth nodes went with the attacker's chain but OpenEthereum nodes stuck with the original chain.We can say that the attack did in fact default to chaos, though this was an accident and not a deliberate design decision of the ETC community. Unfortunately, the community then elected to accept the (longer) attack chain as canonical, a move described by the eth_classic twitter as "following Proof of Work as intended". Hence, the community norms actively helped the attacker win.But we could instead agree on a definition of the canonical chain that works differently: particularly, imagine a rule that once a client has accepted a block as part of the canonical chain, and that block has more than 100 descendants, the client will from then on never accept a chain that does not include that block. Alternatively, in a finality-bearing proof of stake setup (which eg. ethereum 2.0 is), imagine a rule that once a block is finalized it can never be reverted. 5 block revert limit only for illustration purposes; in reality the limit could be something longer like 100-1000 blocks.To be clear, this introduces a significant change to how canonicalness is determined: instead of clients just looking at the data they receive by itself, clients also look at when that data was received. This introduces the possibility that, because of network latency, clients disagree: what if, because of a massive attack, two conflicting blocks A and B finalize at the same time, and some clients see A first and some see B first? But I would argue that this is good: it means that instead of defaulting to victory, even 51% attacks that just try to revert transactions default to chaos, and out-of-band emergency response can choose which of the two blocks the chain continues with. If the protocol is well-designed, forcing an escalation to out-of-band emergency response should be very expensive: in proof of stake, such a thing would require 1/3 of validators sacrificing their deposits and getting slashed.Potentially, we could expand this approach. We could try to make 51% attacks that censor transactions default to chaos too. Research on timeliness detectors pushes things further in the direction of attacks of all types defaulting to failure, though a little chaos remains because timeliness detectors cannot help nodes that are not well-connected and online.For a blockchain community that values immutability, implementing revert limits of this kind are arguably the superior path to take. It is difficult to honestly claim that a blockchain is immutable when no matter how long a transaction has been accepted in a chain, there is always the possibility that some unexpected activity by powerful actors can come along and revert it. Of course, I would claim that even BTC and ETC do already have a revert limit at the extremes; if there was an attack that reverted weeks of activity, the community would likely adopt a user-activated soft fork to reject the attackers' chain. But more definitively agreeing on and formalizing this seems like a step forward.ConclusionThere are a few "morals of the story" here. First, if we accept the legitimacy of social coordination, and we accept the legitimacy of indirect validation involving "1-of-N" trust models (that is, assuming that there exists one honest person in the network somewhere; NOT the same as assuming that one specific party, eg. Infura, is honest), then we can create blockchains that are much more scalable.Second, client-side validation is extremely important for all of this to work. A network where only a few people run nodes and everyone else really does trust them is a network that can easily be taken over by special interests. But avoiding such a fate does not require going to the opposite extreme and having everyone always validate everything! Systems that allow each individual block to be verified in isolation, so users only validate blocks if someone else raises an alarm, are totally reasonable and serve the same effect. But this requires accepting the "coordination view" of what validation is for.Third, if we allow the definition of canonicalness includes timing, then we open many doors in improving our ability to reject 51% attacks. The easiest property to gain is weak subjectivity: the idea that if clients are required to log on at least once every eg. 3 months, and refuse to revert longer than that, then we can add slashing to proof of stake and make attacks very expensive. But we can go further: we can reject chains that revert finalized blocks and thereby protect immutability, and even protect against censorship. Because the network is unpredictable, relying on timing does imply attacks "defaulting to chaos" in some cases, but the benefits are very much worth it.With all of these ideas in mind, we can avoid the traps of (i) over-centralization, (ii) overly redundant verification leading to inefficiency and (iii) misguided norms accidentally making attacks easier, and better work toward building more resilient, performant and secure blockchains. -
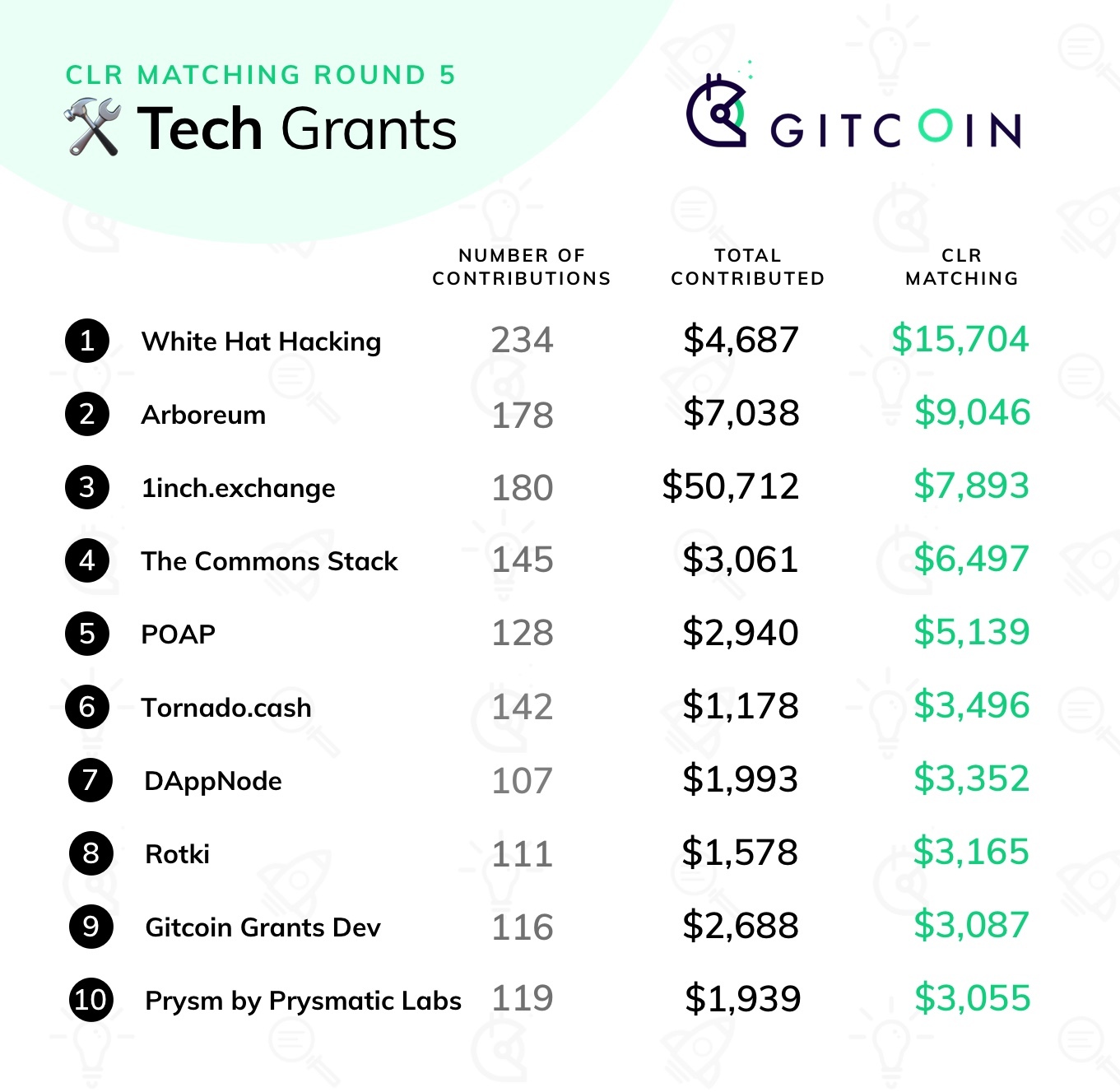
 Gitcoin Grants Round 5 Retrospective Gitcoin Grants Round 5 Retrospective2020 Apr 30 See all posts Gitcoin Grants Round 5 Retrospective Special thanks to Kevin Owocki and Frank Chen for help and reviewRound 5 of Gitcoin Grants has just finished, with $250,000 of matching split between tech, media, and the new (non-Ethereum-centric) category of "public health". In general, it seems like the mechanism and the community are settling down into a regular rhythm. People know what it means to contribute, people know what to expect, and the results emerge in a relatively predictable pattern - even if which specific grants get the most funds is not so easy to predict. Stability of incomeSo let's go straight into the analysis. One important property worth looking at is stability of income across rounds: do projects that do well in round N also tend to do well in round N+1? Stability of income is very important if we want to support an ecosystem of "quadratic freelancers": we want people to feel comfortable relying on their income knowing that it will not completely disappear the next round. On the other hand, it would be harmful if some recipients became completely entrenched, with no opportunity for new projects to come in and compete for the pot, so there is a need for a balance.On the media side, we do see some balance between stability and dynamism: Week in Ethereum had the highest total amount received in both the previous round and the current round. EthHub and Bankless are also near the top in both the current round and the previous round. On the other hand, Antiprosynthesis, the (beloved? notorious? famous?) Twitter info-warrior, has decreased from $13,813 to $5,350, while Chris Blec's YouTube channel has increased from $5,851 to $12,803. So some churn, but also some continuity between rounds.On the tech side, we see much more churn in the winners, with a less clear relationship between income last round and income this round: Last round, the winner was Tornado Cash, claiming $30,783; this round, they are down to $8,154. This round, the three roughly-even winners are Samczsun ($4,631 contributions + $15,704 match = $20,335 total), Arboreum ($16,084 contributions + $9,046 match = $25,128 total) and 1inch.exchange ($58,566 contributions + $7,893 match = $66,459 total), in the latter case the bulk coming from one contribution: In the previous round, those three winners were not even in the top ten, and in some cases not even part of Gitcoin Grants at all.These numbers show us two things. First, large parts of the Gitcoin community seem to be in the mindset of treating grants not as a question of "how much do you deserve for your last two months of work?", but rather as a one-off reward for years of contributions in the past. This was one of the strongest rebuttals that I received to my criticism of Antiprosynthesis receiving $13,813 in the last round: that the people who contributed to that award did not see it as two months' salary, but rather as a reward for years of dedication and work for the Ethereum ecosystem. In the next round, contributors were content that the debt was sufficiently repaid, and so they moved on to give a similar gift of appreciation and gratitude to Chris Blec.That said, not everyone contributes in this way. For example, Prysm got $7,966 last round and $8,033 this round, and Week in Ethereum is consistently well-rewarded ($16,727 previous, $12,195 current), and EthHub saw less stability but still kept half its income ($13,515 previous, $6,705 current) even amid a 20% drop to the matching pool size as some funds were redirected to public health. So there definitely are some contributors that are getting almost a reasonable monthly salary from Gitcoin Grants (yes, even these amounts are all serious underpayment, but remember that the pool of funds Gitcoin Grants has to distribute in the first place is quite small, so there's no allocation that would not seriously underpay most people; the hope is that in the future we will find ways to make the matching pot grow bigger).Why didn't more people use recurring contributions?One feature that was tested this round to try to improve stability was recurring contributions: users could choose to split their contribution among multiple rounds. However, the feature was not used often: out of over 8,000 total contributions, only 120 actually made recurring contributions. I can think of three possible explanations for this:People just don't want to give recurring contributions; they genuinely prefer to freshly rethink who they are supporting every round. People would be willing to give more recurring contributions, but there is some kind of "market failure" stopping them; that is, it's collectively optimal for everyone to give more recurring contributions, but it's not any individual contributor's interest to be the first to do so. There's some UI inconveniences or other "incidental" obstacles preventing recurring contributions. In a recent call with the Gitcoin team, hypothesis (3) was mentioned frequently. A specific issue was that people were worried about making recurring contributions because they were concerned whether or not the money that they lock up for a recurring contribution would be safe. Improving the payment system and notification workflow may help with this. Another option is to move away from explicit "streaming" and instead simply have the UI provide an option for repeating the last round's contributions and making edits from there.Hypothesis (1) also should be taken seriously; there's genuine value in preventing ossification and allowing space for new entrants. But I want to zoom in particularly on hypothesis (2), the coordination failure hypothesis.My explanation of hypothesis (2) starts, interestingly enough, with a defense of (1): why ossification is genuinely a risk. Suppose that there are two projects, A and B, and suppose that they are equal quality. But A already has an established base of contributors; B does not (we'll say for illustration it only has a few existing contributors). Here's how much matching you are contributing by participating in each project:Contributing to A Contributing to B Clearly, you have more impact by supporting A, and so A gets even more contributors and B gets fewer; the rich get richer. Even if project B was somewhat better, the greater impact from supporting A could still create a lock-in that reinforces A's position. The current everyone-starts-from-zero-in-each-round mechanism greatly limits this type of entrenchment, because, well, everyone's matching gets reset and starts from zero.However, a very similar effect also is the cause behind the market failure preventing stable recurring contributions, and the every-round-reset actually exacerbates it. Look at the same picture above, except instead of thinking of A and B as two different projects, think of them as the same project in the current round and in the next round.We simplify the model as follows. An individual has two choices: contribute $10 in the current round, or contribute $5 in the current round and $5 in the next round. If the matchings in the two rounds were equal, then the latter option would actually be more favorable: because the matching is proportional to the square root of the donation size, the former might give you eg. a $200 match now, but the latter would give you $141 in the current round + $141 in the next round = $282. But if you see a large mass of people contributing in the current round, and you expect much fewer people to contribute in the second round, then the choice is not $200 versus $141 + $141, it might be $200 versus $141 + $5. And so you're better off joining the current round's frenzy. We can mathematically analyze the equilibrium: So there is a substantial region within which the bad equilibrium of everyone concentrating is sticky: if more than about 3/4 of contributors are expected to concentrate, it seems in your interest to also concentrate. A mathematically astute reader may note that there is always some intermediate strategy that involves splitting but at a ratio different from 50/50, which you can prove performs better than either full concentrating or the even split, but here we get back to hypothesis (3) above: the UI doesn't offer such a complex menu of choices, it just offers the choice of a one-time contribution or a recurring contribution, so people pick one or the other.How might we fix this? One option is to add a bit of continuity to matching ratios: when computing pairwise matches, match against not just the current round's contributors but, say, 1/3 of the previous round's contributors as well: This makes some philosophical sense: the objective of quadratic funding is to subsidize contributions to projects that are detected to be public goods because multiple people have contributed to them, and contributions in the previous round are certainly also evidence of a project's value, so why not reuse those? So here, moving away from everyone-starts-from-zero toward this partial carryover of matching ratios would mitigate the round concentration effect - but, of course, it would exacerbate the risk of entrenchment. Hence, some experimentation and balance may be in order. A broader philosophical question is, is there really a deep inherent tradeoff between risk of entrenchment and stability of income, or is there some way we could get both?Responses to negative contributionsThis round also introduced negative contributions, a feature proposed in my review of the previous round. But as with recurring contributions, very few people made negative contributions, to the point where their impact on the results was negligible. Also, there was active opposition to negative contributions: Source: honestly I have no idea, someone else sent it to me and they forgot where they found it. Sorry :( The main source of opposition was basically what I predicted in the previous round. Adding a mechanism that allows people to penalize others, even if deservedly so, can have tricky and easily harmful social consequences. Some people even opposed the negative contribution mechanism to the point where they took care to give positive contributions to everyone who received a negative contribution.How do we respond? To me it seems clear that, in the long run, some mechanism of filtering out bad projects, and ideally compensating for overexcitement into good projects, will have to exist. It doesn't necessarily need to be integrated as a symmetric part of the QF, but there does need to be a filter of some form. And this mechanism, whatever form it will take, invariably opens up the possibility of the same social dynamics. So there is a challenge that will have to be solved no matter how we do it.One approach would be to hide more information: instead of just hiding who made a negative contribution, outright hide the fact that a negative contribution was made. Many opponents of negative contributions explicitly indicated that they would be okay (or at least more okay) with such a model. And indeed (see the next section), this is a direction we will have to go anyway. But it would come at a cost - effectively hiding negative contributions would mean not giving as much real-time feedback into what projects got how much funds.Stepping up the fight against collusionThis round saw much larger-scale attempts at collusion: It does seem clear that, at current scales, stronger protections against manipulation are goingto be required. The first thing that can be done is adding a stronger identity verification layer than Github accounts; this is something that the Gitcoin team is already working on. There is definitely a complex tradeoff between security and inclusiveness to be worked through, but it is not especially difficult to implement a first version. And if the identity problem is solved to a reasonable extent, that will likely be enough to prevent collusion at current scales. But in the longer term, we are going to need protection not just against manipulating the system by making many fake accounts, but also against collusion via bribes (explicit and implicit).MACI is the solution that I proposed (and Barry Whitehat and co are implementing) to solve this problem. Essentially, MACI is a cryptographic construction that allows for contributions to projects to happen on-chain in a privacy-preserving, encrypted form, that allows anyone to cryptographically verify that the mechanism is being implemented correctly, but prevents participants from being able to prove to a third party that they made any particular contribution. Unprovability means that if someone tries to bribe others to contribute to their project, the bribe recipients would have no way to prove that they actually contributed to that project, making the bribe unenforceable. Benign "collusion" in the form of friends and family supporting each other would still happen, as people would not easily lie to each other at such small scales, but any broader collusion would be very difficult to maintain.However, we do need to think through some of the second-order consequences that integrating MACI would introduce. The biggest blessing, and curse, of using MACI is that contributions become hidden. Identities necessarily become hidden, but even the exact timing of contributions would need to be hidden to prevent deanonymization through timing (to prove that you contributed, make the total amount jump up between 17:40 and 17:42 today). Instead, for example, totals could be provided and updated once per day. Note that as a corollary negative contributions would be hidden as well; they would only appear if they exceeded all positive contributions for an entire day (and if even that is not desired then the mechanism for when balances are updated could be tweaked to further hide downward changes).The challenge with hiding contributions is that we lose the "social proof" motivator for contributing: if contributions are unprovable you can't as easily publicly brag about a contribution you made. My best proposal for solving this is for the mechanism to publish one extra number: the total amount that a particular participant contributed (counting only projects that have received at least 10 contributors to prevent inflating one's number by self-dealing). Individuals would then have a generic "proof-of-generosity" that they contributed some specific total amount, and could publicly state (without proof) what projects it was that they supported. But this is all a significant change to the user experience that will require multiple rounds of experimentation to get right.ConclusionsAll in all, Gitcoin Grants is establishing itself as a significant pillar of the Ethereum ecosystem that more and more projects are relying on for some or all of their support. While it has a relatively low amount of funding at present, and so inevitably underfunds almost everything it touches, we hope that over time we'll continue to see larger sources of funding for the matching pools appear. One option is MEV auctions, another is that new or existing token projects looking to do airdrops could provide the tokens to a matching pool. A third is transaction fees of various applications. With larger amounts of funding, Gitcoin Grants could serve as a more significant funding stream - though to get to that point, further iteration and work on fine-tuning the mechanism will be required. Additionally, this round saw Gitcoin Grants' first foray into applications beyond Ethereum with the health section. There is growing interest in quadratic funding from local government bodies and other non-blockchain groups, and it would be very valuable to see quadratic funding more broadly deployed in such contexts. That said, there are unique challenges there too. First, there's issues around onboarding people who do not already have cryptocurrency. Second, the Ethereum community is naturally expert in the needs of the Ethereum community, but neither it nor average people are expert in, eg. medical support for the coronavirus pandemic. We should expect quadratic funding to perform worse when the participants are not experts in the domain they're being asked to contribute to. Will non-blockchain uses of QF focus on domains where there's a clear local community that's expert in its own needs, or will people try larger-scale deployments soon? If we do see larger-scale deployments, how will those turn out? There's still a lot of questions to be answered.
Gitcoin Grants Round 5 Retrospective Gitcoin Grants Round 5 Retrospective2020 Apr 30 See all posts Gitcoin Grants Round 5 Retrospective Special thanks to Kevin Owocki and Frank Chen for help and reviewRound 5 of Gitcoin Grants has just finished, with $250,000 of matching split between tech, media, and the new (non-Ethereum-centric) category of "public health". In general, it seems like the mechanism and the community are settling down into a regular rhythm. People know what it means to contribute, people know what to expect, and the results emerge in a relatively predictable pattern - even if which specific grants get the most funds is not so easy to predict. Stability of incomeSo let's go straight into the analysis. One important property worth looking at is stability of income across rounds: do projects that do well in round N also tend to do well in round N+1? Stability of income is very important if we want to support an ecosystem of "quadratic freelancers": we want people to feel comfortable relying on their income knowing that it will not completely disappear the next round. On the other hand, it would be harmful if some recipients became completely entrenched, with no opportunity for new projects to come in and compete for the pot, so there is a need for a balance.On the media side, we do see some balance between stability and dynamism: Week in Ethereum had the highest total amount received in both the previous round and the current round. EthHub and Bankless are also near the top in both the current round and the previous round. On the other hand, Antiprosynthesis, the (beloved? notorious? famous?) Twitter info-warrior, has decreased from $13,813 to $5,350, while Chris Blec's YouTube channel has increased from $5,851 to $12,803. So some churn, but also some continuity between rounds.On the tech side, we see much more churn in the winners, with a less clear relationship between income last round and income this round: Last round, the winner was Tornado Cash, claiming $30,783; this round, they are down to $8,154. This round, the three roughly-even winners are Samczsun ($4,631 contributions + $15,704 match = $20,335 total), Arboreum ($16,084 contributions + $9,046 match = $25,128 total) and 1inch.exchange ($58,566 contributions + $7,893 match = $66,459 total), in the latter case the bulk coming from one contribution: In the previous round, those three winners were not even in the top ten, and in some cases not even part of Gitcoin Grants at all.These numbers show us two things. First, large parts of the Gitcoin community seem to be in the mindset of treating grants not as a question of "how much do you deserve for your last two months of work?", but rather as a one-off reward for years of contributions in the past. This was one of the strongest rebuttals that I received to my criticism of Antiprosynthesis receiving $13,813 in the last round: that the people who contributed to that award did not see it as two months' salary, but rather as a reward for years of dedication and work for the Ethereum ecosystem. In the next round, contributors were content that the debt was sufficiently repaid, and so they moved on to give a similar gift of appreciation and gratitude to Chris Blec.That said, not everyone contributes in this way. For example, Prysm got $7,966 last round and $8,033 this round, and Week in Ethereum is consistently well-rewarded ($16,727 previous, $12,195 current), and EthHub saw less stability but still kept half its income ($13,515 previous, $6,705 current) even amid a 20% drop to the matching pool size as some funds were redirected to public health. So there definitely are some contributors that are getting almost a reasonable monthly salary from Gitcoin Grants (yes, even these amounts are all serious underpayment, but remember that the pool of funds Gitcoin Grants has to distribute in the first place is quite small, so there's no allocation that would not seriously underpay most people; the hope is that in the future we will find ways to make the matching pot grow bigger).Why didn't more people use recurring contributions?One feature that was tested this round to try to improve stability was recurring contributions: users could choose to split their contribution among multiple rounds. However, the feature was not used often: out of over 8,000 total contributions, only 120 actually made recurring contributions. I can think of three possible explanations for this:People just don't want to give recurring contributions; they genuinely prefer to freshly rethink who they are supporting every round. People would be willing to give more recurring contributions, but there is some kind of "market failure" stopping them; that is, it's collectively optimal for everyone to give more recurring contributions, but it's not any individual contributor's interest to be the first to do so. There's some UI inconveniences or other "incidental" obstacles preventing recurring contributions. In a recent call with the Gitcoin team, hypothesis (3) was mentioned frequently. A specific issue was that people were worried about making recurring contributions because they were concerned whether or not the money that they lock up for a recurring contribution would be safe. Improving the payment system and notification workflow may help with this. Another option is to move away from explicit "streaming" and instead simply have the UI provide an option for repeating the last round's contributions and making edits from there.Hypothesis (1) also should be taken seriously; there's genuine value in preventing ossification and allowing space for new entrants. But I want to zoom in particularly on hypothesis (2), the coordination failure hypothesis.My explanation of hypothesis (2) starts, interestingly enough, with a defense of (1): why ossification is genuinely a risk. Suppose that there are two projects, A and B, and suppose that they are equal quality. But A already has an established base of contributors; B does not (we'll say for illustration it only has a few existing contributors). Here's how much matching you are contributing by participating in each project:Contributing to A Contributing to B Clearly, you have more impact by supporting A, and so A gets even more contributors and B gets fewer; the rich get richer. Even if project B was somewhat better, the greater impact from supporting A could still create a lock-in that reinforces A's position. The current everyone-starts-from-zero-in-each-round mechanism greatly limits this type of entrenchment, because, well, everyone's matching gets reset and starts from zero.However, a very similar effect also is the cause behind the market failure preventing stable recurring contributions, and the every-round-reset actually exacerbates it. Look at the same picture above, except instead of thinking of A and B as two different projects, think of them as the same project in the current round and in the next round.We simplify the model as follows. An individual has two choices: contribute $10 in the current round, or contribute $5 in the current round and $5 in the next round. If the matchings in the two rounds were equal, then the latter option would actually be more favorable: because the matching is proportional to the square root of the donation size, the former might give you eg. a $200 match now, but the latter would give you $141 in the current round + $141 in the next round = $282. But if you see a large mass of people contributing in the current round, and you expect much fewer people to contribute in the second round, then the choice is not $200 versus $141 + $141, it might be $200 versus $141 + $5. And so you're better off joining the current round's frenzy. We can mathematically analyze the equilibrium: So there is a substantial region within which the bad equilibrium of everyone concentrating is sticky: if more than about 3/4 of contributors are expected to concentrate, it seems in your interest to also concentrate. A mathematically astute reader may note that there is always some intermediate strategy that involves splitting but at a ratio different from 50/50, which you can prove performs better than either full concentrating or the even split, but here we get back to hypothesis (3) above: the UI doesn't offer such a complex menu of choices, it just offers the choice of a one-time contribution or a recurring contribution, so people pick one or the other.How might we fix this? One option is to add a bit of continuity to matching ratios: when computing pairwise matches, match against not just the current round's contributors but, say, 1/3 of the previous round's contributors as well: This makes some philosophical sense: the objective of quadratic funding is to subsidize contributions to projects that are detected to be public goods because multiple people have contributed to them, and contributions in the previous round are certainly also evidence of a project's value, so why not reuse those? So here, moving away from everyone-starts-from-zero toward this partial carryover of matching ratios would mitigate the round concentration effect - but, of course, it would exacerbate the risk of entrenchment. Hence, some experimentation and balance may be in order. A broader philosophical question is, is there really a deep inherent tradeoff between risk of entrenchment and stability of income, or is there some way we could get both?Responses to negative contributionsThis round also introduced negative contributions, a feature proposed in my review of the previous round. But as with recurring contributions, very few people made negative contributions, to the point where their impact on the results was negligible. Also, there was active opposition to negative contributions: Source: honestly I have no idea, someone else sent it to me and they forgot where they found it. Sorry :( The main source of opposition was basically what I predicted in the previous round. Adding a mechanism that allows people to penalize others, even if deservedly so, can have tricky and easily harmful social consequences. Some people even opposed the negative contribution mechanism to the point where they took care to give positive contributions to everyone who received a negative contribution.How do we respond? To me it seems clear that, in the long run, some mechanism of filtering out bad projects, and ideally compensating for overexcitement into good projects, will have to exist. It doesn't necessarily need to be integrated as a symmetric part of the QF, but there does need to be a filter of some form. And this mechanism, whatever form it will take, invariably opens up the possibility of the same social dynamics. So there is a challenge that will have to be solved no matter how we do it.One approach would be to hide more information: instead of just hiding who made a negative contribution, outright hide the fact that a negative contribution was made. Many opponents of negative contributions explicitly indicated that they would be okay (or at least more okay) with such a model. And indeed (see the next section), this is a direction we will have to go anyway. But it would come at a cost - effectively hiding negative contributions would mean not giving as much real-time feedback into what projects got how much funds.Stepping up the fight against collusionThis round saw much larger-scale attempts at collusion: It does seem clear that, at current scales, stronger protections against manipulation are goingto be required. The first thing that can be done is adding a stronger identity verification layer than Github accounts; this is something that the Gitcoin team is already working on. There is definitely a complex tradeoff between security and inclusiveness to be worked through, but it is not especially difficult to implement a first version. And if the identity problem is solved to a reasonable extent, that will likely be enough to prevent collusion at current scales. But in the longer term, we are going to need protection not just against manipulating the system by making many fake accounts, but also against collusion via bribes (explicit and implicit).MACI is the solution that I proposed (and Barry Whitehat and co are implementing) to solve this problem. Essentially, MACI is a cryptographic construction that allows for contributions to projects to happen on-chain in a privacy-preserving, encrypted form, that allows anyone to cryptographically verify that the mechanism is being implemented correctly, but prevents participants from being able to prove to a third party that they made any particular contribution. Unprovability means that if someone tries to bribe others to contribute to their project, the bribe recipients would have no way to prove that they actually contributed to that project, making the bribe unenforceable. Benign "collusion" in the form of friends and family supporting each other would still happen, as people would not easily lie to each other at such small scales, but any broader collusion would be very difficult to maintain.However, we do need to think through some of the second-order consequences that integrating MACI would introduce. The biggest blessing, and curse, of using MACI is that contributions become hidden. Identities necessarily become hidden, but even the exact timing of contributions would need to be hidden to prevent deanonymization through timing (to prove that you contributed, make the total amount jump up between 17:40 and 17:42 today). Instead, for example, totals could be provided and updated once per day. Note that as a corollary negative contributions would be hidden as well; they would only appear if they exceeded all positive contributions for an entire day (and if even that is not desired then the mechanism for when balances are updated could be tweaked to further hide downward changes).The challenge with hiding contributions is that we lose the "social proof" motivator for contributing: if contributions are unprovable you can't as easily publicly brag about a contribution you made. My best proposal for solving this is for the mechanism to publish one extra number: the total amount that a particular participant contributed (counting only projects that have received at least 10 contributors to prevent inflating one's number by self-dealing). Individuals would then have a generic "proof-of-generosity" that they contributed some specific total amount, and could publicly state (without proof) what projects it was that they supported. But this is all a significant change to the user experience that will require multiple rounds of experimentation to get right.ConclusionsAll in all, Gitcoin Grants is establishing itself as a significant pillar of the Ethereum ecosystem that more and more projects are relying on for some or all of their support. While it has a relatively low amount of funding at present, and so inevitably underfunds almost everything it touches, we hope that over time we'll continue to see larger sources of funding for the matching pools appear. One option is MEV auctions, another is that new or existing token projects looking to do airdrops could provide the tokens to a matching pool. A third is transaction fees of various applications. With larger amounts of funding, Gitcoin Grants could serve as a more significant funding stream - though to get to that point, further iteration and work on fine-tuning the mechanism will be required. Additionally, this round saw Gitcoin Grants' first foray into applications beyond Ethereum with the health section. There is growing interest in quadratic funding from local government bodies and other non-blockchain groups, and it would be very valuable to see quadratic funding more broadly deployed in such contexts. That said, there are unique challenges there too. First, there's issues around onboarding people who do not already have cryptocurrency. Second, the Ethereum community is naturally expert in the needs of the Ethereum community, but neither it nor average people are expert in, eg. medical support for the coronavirus pandemic. We should expect quadratic funding to perform worse when the participants are not experts in the domain they're being asked to contribute to. Will non-blockchain uses of QF focus on domains where there's a clear local community that's expert in its own needs, or will people try larger-scale deployments soon? If we do see larger-scale deployments, how will those turn out? There's still a lot of questions to be answered. -
 Exploring Fully Homomorphic Encryption Exploring Fully Homomorphic Encryption2020 Jul 20 See all posts Exploring Fully Homomorphic Encryption Special thanks to Karl Floersch and Dankrad Feist for reviewFully homomorphic encryption has for a long time been considered one of the holy grails of cryptography. The promise of fully homomorphic encryption (FHE) is powerful: it is a type of encryption that allows a third party to perform computations on encrypted data, and get an encrypted result that they can hand back to whoever has the decryption key for the original data, without the third party being able to decrypt the data or the result themselves. As a simple example, imagine that you have a set of emails, and you want to use a third party spam filter to check whether or not they are spam. The spam filter has a desire for privacy of their algorithm: either the spam filter provider wants to keep their source code closed, or the spam filter depends on a very large database that they do not want to reveal publicly as that would make attacking easier, or both. However, you care about the privacy of your data, and don't want to upload your unencrypted emails to a third party. So here's how you do it: Fully homomorphic encryption has many applications, including in the blockchain space. One key example is that can be used to implement privacy-preserving light clients (the light client hands the server an encrypted index i, the server computes and returns data[0] * (i = 0) + data[1] * (i = 1) + ... + data[n] * (i = n), where data[i] is the i'th piece of data in a block or state along with its Merkle branch and (i = k) is an expression that returns 1 if i = k and otherwise 0; the light client gets the data it needs and the server learns nothing about what the light client asked).It can also be used for:More efficient stealth address protocols, and more generally scalability solutions to privacy-preserving protocols that today require each user to personally scan the entire blockchain for incoming transactions Privacy-preserving data-sharing marketplaces that let users allow some specific computation to be performed on their data while keeping full control of their data for themselves An ingredient in more powerful cryptographic primitives, such as more efficient multi-party computation protocols and perhaps eventually obfuscation And it turns out that fully homomorphic encryption is, conceptually, not that difficult to understand!Partially, Somewhat, Fully homomorphic encryptionFirst, a note on definitions. There are different kinds of homomorphic encryption, some more powerful than others, and they are separated by what kinds of functions one can compute on the encrypted data.Partially homomorphic encryption allows evaluating only a very limited set of operations on encrypted data: either just additions (so given encrypt(a) and encrypt(b) you can compute encrypt(a+b)), or just multiplications (given encrypt(a) and encrypt(b) you can compute encrypt(a*b)). Somewhat homomorphic encryption allows computing additions as well as a limited number of multiplications (alternatively, polynomials up to a limited degree). That is, if you get encrypt(x1) ... encrypt(xn) (assuming these are "original" encryptions and not already the result of homomorphic computation), you can compute encrypt(p(x1 ... xn)), as long as p(x1 ... xn) is a polynomial with degree < D for some specific degree bound D (D is usually very low, think 5-15). Fully homomorphic encryption allows unlimited additions and multiplications. Additions and multiplications let you replicate any binary circuit gates (AND(x, y) = x*y, OR(x, y) = x+y-x*y, XOR(x, y) = x+y-2*x*y or just x+y if you only care about even vs odd, NOT(x) = 1-x...), so this is sufficient to do arbitrary computation on encrypted data. Partially homomorphic encryption is fairly easy; eg. RSA has a multiplicative homomorphism: \(enc(x) = x^e\), \(enc(y) = y^e\), so \(enc(x) * enc(y) = (xy)^e = enc(xy)\). Elliptic curves can offer similar properties with addition. Allowing both addition and multiplication is, it turns out, significantly harder.A simple somewhat-HE algorithmHere, we will go through a somewhat-homomorphic encryption algorithm (ie. one that supports a limited number of multiplications) that is surprisingly simple. A more complex version of this category of technique was used by Craig Gentry to create the first-ever fully homomorphic scheme in 2009. More recent efforts have switched to using different schemes based on vectors and matrices, but we will still go through this technique first.We will describe all of these encryption schemes as secret-key schemes; that is, the same key is used to encrypt and decrypt. Any secret-key HE scheme can be turned into a public key scheme easily: a "public key" is typically just a set of many encryptions of zero, as well as an encryption of one (and possibly more powers of two). To encrypt a value, generate it by adding together the appropriate subset of the non-zero encryptions, and then adding a random subset of the encryptions of zero to "randomize" the ciphertext and make it infeasible to tell what it represents.The secret key here is a large prime, \(p\) (think of \(p\) as having hundreds or even thousands of digits). The scheme can only encrypt 0 or 1, and "addition" becomes XOR, ie. 1 + 1 = 0. To encrypt a value \(m\) (which is either 0 or 1), generate a large random value \(R\) (this will typically be even larger than \(p\)) and a smaller random value \(r\) (typically much smaller than \(p\)), and output:\[enc(m) = R * p + r * 2 + m\]To decrypt a ciphertext \(ct\), compute:\[dec(ct) = (ct\ mod\ p)\ mod\ 2\]To add two ciphertexts \(ct_1\) and \(ct_2\), you simply, well, add them: \(ct_1 + ct_2\). And to multiply two ciphertexts, you once again... multiply them: \(ct_1 * ct_2\). We can prove the homomorphic property (that the sum of the encryptions is an encryption of the sum, and likewise for products) as follows.Let:\[ct_1 = R_1 * p + r_1 * 2 + m_1\] \[ct_2 = R_2 * p + r_2 * 2 + m_2\]We add:\[ct_1 + ct_2 = R_1 * p + R_2 * p + r_1 * 2 + r_2 * 2 + m_1 + m_2\]Which can be rewritten as:\[(R_1 + R_2) * p + (r_1 + r_2) * 2 + (m_1 + m_2)\]Which is of the exact same "form" as a ciphertext of \(m_1 + m_2\). If you decrypt it, the first \(mod\ p\) removes the first term, the second \(mod\ 2\) removes the second term, and what's left is \(m_1 + m_2\) (remember that if \(m_1 = 1\) and \(m_2 = 1\) then the 2 will get absorbed into the second term and you'll be left with zero). And so, voila, we have additive homomorphism!Now let's check multiplication:\[ct_1 * ct_2 = (R_1 * p + r_1 * 2 + m_1) * (R_2 * p + r_2 * 2 + m_2)\]Or:\[(R_1 * R_2 * p + r_1 * 2 + m_1 + r_2 * 2 + m_2) * p + \] \[(r_1 * r_2 * 2 + r_1 * m_2 + r_2 * m_1) * 2 + \] \[(m_1 * m_2)\]This was simply a matter of expanding the product above, and grouping together all the terms that contain \(p\), then all the remaining terms that contain \(2\), and finally the remaining term which is the product of the messages. If you decrypt, then once again the \(mod\ p\) removes the first group, the \(mod\ 2\) removes the second group, and only \(m_1 * m_2\) is left.But there are two problems here: first, the size of the ciphertext itself grows (the length roughly doubles when you multiply), and second, the "noise" (also often called "error") in the smaller \(\* 2\) term also gets quadratically bigger. Adding this error into the ciphertexts was necessary because the security of this scheme is based on the approximate GCD problem: Had we instead used the "exact GCD problem", breaking the system would be easy: if you just had a set of expressions of the form \(p * R_1 + m_1\), \(p * R_2 + m_2\)..., then you could use the Euclidean algorithm to efficiently compute the greatest common divisor \(p\). But if the ciphertexts are only approximate multiples of \(p\) with some "error", then extracting \(p\) quickly becomes impractical, and so the scheme can be secure.Unfortunately, the error introduces the inherent limitation that if you multiply the ciphertexts by each other enough times, the error eventually grows big enough that it exceeds \(p\), and at that point the \(mod\ p\) and \(mod\ 2\) steps "interfere" with each other, making the data unextractable. This will be an inherent tradeoff in all of these homomorphic encryption schemes: extracting information from approximate equations "with errors" is much harder than extracting information from exact equations, but any error you add quickly increases as you do computations on encrypted data, bounding the amount of computation that you can do before the error becomes overwhelming. And this is why these schemes are only "somewhat" homomorphic.BootstrappingThere are two classes of solution to this problem. First, in many somewhat homomorphic encryption schemes, there are clever tricks to make multiplication only increase the error by a constant factor (eg. 1000x) instead of squaring it. Increasing the error by 1000x still sounds by a lot, but keep in mind that if \(p\) (or its equivalent in other schemes) is a 300-digit number, that means that you can multiply numbers by each other 100 times, which is enough to compute a very wide class of computations. Second, there is Craig Gentry's technique of "bootstrapping".Suppose that you have a ciphertext \(ct\) that is an encryption of some \(m\) under a key \(p\), that has a lot of error. The idea is that we "refresh" the ciphertext by turning it into a new ciphertext of \(m\) under another key \(p_2\), where this process "clears out" the old error (though it will introduce a fixed amount of new error). The trick is quite clever. The holder of \(p\) and \(p_2\) provides a "bootstrapping key" that consists of an encryption of the bits of \(p\) under the key \(p_2\), as well as the public key for \(p_2\). Whoever is doing computations on data encrypted under \(p\) would then take the bits of the ciphertext \(ct\), and individually encrypt these bits under \(p_2\). They would then homomorphically compute the decryption under \(p\) using these ciphertexts, and get out the single bit, which would be \(m\) encrypted under \(p_2\). This is difficult to understand, so we can restate it as follows. The decryption procedure \(dec(ct, p)\) is itself a computation, and so it can itself be implemented as a circuit that takes as input the bits of \(ct\) and the bits of \(p\), and outputs the decrypted bit \(m \in \). If someone has a ciphertext \(ct\) encrypted under \(p\), a public key for \(p_2\), and the bits of \(p\) encrypted under \(p_2\), then they can compute \(dec(ct, p) = m\) "homomorphically", and get out \(m\) encrypted under \(p_2\). Notice that the decryption procedure itself washes away the old error; it just outputs 0 or 1. The decryption procedure is itself a circuit, which contains additions or multiplications, so it will introduce new error, but this new error does not depend on the amount of error in the original encryption.(Note that we can avoid having a distinct new key \(p_2\) (and if you want to bootstrap multiple times, also a \(p_3\), \(p_4\)...) by just setting \(p_2 = p\). However, this introduces a new assumption, usually called "circular security"; it becomes more difficult to formally prove security if you do this, though many cryptographers think it's fine and circular security poses no significant risk in practice)But.... there is a catch. In the scheme as described above (using circular security or not), the error blows up so quickly that even the decryption circuit of the scheme itself is too much for it. That is, the new \(m\) encrypted under \(p_2\) would already have so much error that it is unreadable. This is because each AND gate doubles the bit-length of the error, so a scheme using a \(d\)-bit modulus \(p\) can only handle less than \(log(d)\) multiplications (in series), but decryption requires computing \(mod\ p\) in a circuit made up of these binary logic gates, which requires... more than \(log(d)\) multiplications.Craig Gentry came up with clever techniques to get around this problem, but they are arguably too complicated to explain; instead, we will skip straight to newer work from 2011 and 2013, that solves this problem in a different way.Learning with errorsTo move further, we will introduce a different type of somewhat-homomorphic encryption introduced by Brakerski and Vaikuntanathan in 2011, and show how to bootstrap it. Here, we will move away from keys and ciphertexts being integers, and instead have keys and ciphertexts be vectors. Given a key \(k = \), to encrypt a message \(m\), construct a vector \(c = \) such that the inner product (or "dot product") \( = c_1k_1 + c_2k_1 + ... + c_nk_n\), modulo some fixed number \(p\), equals \(m+2e\) where \(m\) is the message (which must be 0 or 1), and \(e\) is a small (much smaller than \(p\)) "error" term. A "public key" that allows encryption but not decryption can be constructed, as before, by making a set of encryptions of 0; an encryptor can randomly combine a subset of these equations and add 1 if the message they are encrypting is 1. To decrypt a ciphertext \(c\) knowing the key \(k\), you would compute \(\) modulo \(p\), and see if the result is odd or even (this is the same "mod p mod 2" trick we used earlier). Note that here the \(mod\ p\) is typically a "symmetric" mod, that is, it returns a number between \(-\frac\) and \(\frac\) (eg. 137 mod 10 = -3, 212 mod 10 = 2); this allows our error to be positive or negative. Additionally, \(p\) does not necessarily have to be prime, though it does need to be odd. Key 3 14 15 92 65 Ciphertext 2 71 82 81 8 The key and the ciphertext are both vectors, in this example of five elements each.In this example, we set the modulus \(p = 103\). The dot product is 3 * 2 + 14 * 71 + 15 * 82 + 92 * 81 + 65 * 8 = 10202, and \(10202 = 99 * 103 + 5\). 5 itself is of course \(2 * 2 + 1\), so the message is 1. Note that in practice, the first element of the key is often set to \(1\); this makes it easier to generate ciphertexts for a particular value (see if you can figure out why).The security of the scheme is based on an assumption known as "learning with errors" (LWE) - or, in more jargony but also more understandable terms, the hardness of solving systems of equations with errors. A ciphertext can itself be viewed as an equation: \(k_1c_1 + .... + k_nc_n \approx 0\), where the key \(k_1 ... k_n\) is the unknowns, the ciphertext \(c_1 ... c_n\) is the coefficients, and the equality is only approximate because of both the message (0 or 1) and the error (\(2e\) for some relatively small \(e\)). The LWE assumption ensures that even if you have access to many of these ciphertexts, you cannot recover \(k\).Note that in some descriptions of LWE, can equal any value, but this value must be provided as part of the ciphertext. This is mathematically equivalent to the = m+2e formulation, because you can just add this answer to the end of the ciphertext and add -1 to the end of the key, and get two vectors that when multiplied together just give m+2e. We'll use the formulation that requires to be near-zero (ie. just m+2e) because it is simpler to work with.Multiplying ciphertextsIt is easy to verify that the encryption is additive: if \( = 2e_1 + m_1\) and \( = 2e_2 + m_2\), then \( = 2(e_1 + e_2) + m_1 + m_2\) (the addition here is modulo \(p\)). What is harder is multiplication: unlike with numbers, there is no natural way to multiply two length-n vectors into another length-n vector. The best that we can do is the outer product: a vector containing the products of each possible pair where the first element comes from the first vector and the second element comes from the second vector. That is, \(a \otimes b = a_1b_1 + a_2b_1 + ... + a_nb_1 + a_1b_2 + ... + a_nb_2 + ... + a_nb_n\). We can "multiply ciphertexts" using the convenient mathematical identity \( = * \).Given two ciphertexts \(c_1\) and \(c_2\), we compute the outer product \(c_1 \otimes c_2\). If both \(c_1\) and \(c_2\) were encrypted with \(k\), then \( = 2e_1 + m_1\) and \( = 2e_2 + m_2\). The outer product \(c_1 \otimes c_2\) can be viewed as an encryption of \(m_1 * m_2\) under \(k \otimes k\); we can see this by looking what happens when we try to decrypt with \(k \otimes k\):\[\] \[= * \] \[ = (2e_1 + m_1) * (2e_2 + m_2)\] \[ = 2(e_1m_2 + e_2m_1 + 2e_1e_2) + m_1m_2\]So this outer-product approach works. But there is, as you may have already noticed, a catch: the size of the ciphertext, and the key, grows quadratically.RelinearizationWe solve this with a relinearization procedure. The holder of the private key \(k\) provides, as part of the public key, a "relinearization key", which you can think of as "noisy" encryptions of \(k \otimes k\) under \(k\). The idea is that we provide these encrypted pieces of \(k \otimes k\) to anyone performing the computations, allowing them to compute the equation \(\) to "decrypt" the ciphertext, but only in such a way that the output comes back encrypted under \(k\).It's important to understand what we mean here by "noisy encryptions". Normally, this encryption scheme only allows encrypting \(m \in \\), and an "encryption of \(m\)" is a vector \(c\) such that \( = m+2e\) for some small error \(e\). Here, we're "encrypting" arbitrary \(m \in \\). Note that the error means that you can't fully recover \(m\) from \(c\); your answer will be off by some multiple of 2. However, it turns out that, for this specific use case, this is fine.The relinearization key consists of a set of vectors which, when inner-producted (modulo \(p\)) with the key \(k\), give values of the form \(k_i * k_j * 2^d + 2e\) (mod \(p\)), one such vector for every possible triple \((i, j, d)\), where \(i\) and \(j\) are indices in the key and \(d\) is an exponent where \(2^d < p\) (note: if the key has length \(n\), there would be \(n^2 * log(p)\) values in the relinearization key; make sure you understand why before continuing). Example assuming p = 15 and k has length 2. Formally, enc(x) here means "outputs x+2e if inner-producted with k".Now, let us take a step back and look again at our goal. We have a ciphertext which, if decrypted with \(k \otimes k\), gives \(m_1 * m_2\). We want a ciphertext which, if decrypted with \(k\), gives \(m_1 * m_2\). We can do this with the relinearization key. Notice that the decryption equation \(\) is just a big sum of terms of the form \((ct_ * ct_) * k_p * k_q\).And what do we have in our relinearization key? A bunch of elements of the form \(2^d * k_p * k_q\), noisy-encrypted under \(k\), for every possible combination of \(p\) and \(q\)! Having all the powers of two in our relinearization key allows us to generate any \((ct_ * ct_) * k_p * k_q\) by just adding up \(\le log(p)\) powers of two (eg. 13 = 8 + 4 + 1) together for each \((p, q)\) pair.For example, if \(ct_1 = [1, 2]\) and \(ct_2 = [3, 4]\), then \(ct_1 \otimes ct_2 = [3, 4, 6, 8]\), and \(enc() = enc(3k_1k_1 + 4k_1k_2 + 6k_2k_1 + 8k_2k_2)\) could be computed via:\[enc(k_1 * k_1) + enc(k_1 * k_1 * 2) + enc(k_1 * k_2 * 4) + \]\[enc(k_2 * k_1 * 2) + enc(k_2 * k_1 * 4) + enc(k_2 * k_2 * 8) \]Note that each noisy-encryption in the relinearization key has some even error \(2e\), and the equation \(\) itself has some error: if \( = 2e_1 + m_1\) and \( = 2e_2 + m_2\), then \( =\) \( * =\) \(2(2e_1e_2 + e_1m_2 + e_2m_1) + m_1m_2\). But this total error is still (relatively) small (\(2e_1e_2 + e_1m_2 + e_2m_1\) plus \(n^2 * log(p)\) fixed-size errors from the realinearization key), and the error is even, and so the result of this calculation still gives a value which, when inner-producted with \(k\), gives \(m_1 * m_2 + 2e'\) for some "combined error" \(e'\).The broader technique we used here is a common trick in homomorphic encryption: provide pieces of the key encrypted under the key itself (or a different key if you are pedantic about avoiding circular security assumptions), such that someone computing on the data can compute the decryption equation, but only in such a way that the output itself is still encrypted. It was used in bootstrapping above, and it's used here; it's best to make sure you mentally understand what's going on in both cases.This new ciphertext has considerably more error in it: the \(n^2 * log(p)\) different errors from the portions of the relinearization key that we used, plus the \(2(2e_1e_2 + e_1m_2 + e_2m_1)\) from the original outer-product ciphertext. Hence, the new ciphertext still does have quadratically larger error than the original ciphertexts, and so we still haven't solved the problem that the error blows up too quickly. To solve this, we move on to another trick...Modulus switchingHere, we need to understand an important algebraic fact. A ciphertext is a vector \(ct\), such that \( = m+2e\), where \(m \in \\). But we can also look at the ciphertext from a different "perspective": consider \(\frac\) (modulo \(p\)). \( = \frac + e\), where \(\frac \in \\}\). Note that because (modulo \(p\)) \((\frac)*2 = p+1 = 1\), division by 2 (modulo \(p\)) maps \(1\) to \(\frac\); this is a very convenient fact for us. The scheme in this section uses both modular division (ie. multiplying by the modular multiplicative inverse) and regular "rounded down" integer division; make sure you understand how both work and how they are different from each other.That is, the operation of dividing by 2 (modulo \(p\)) converts small even numbers into small numbers, and it converts 1 into \(\frac\) (rounded up). So if we look at \(\frac\) (modulo \(p\)) instead of \(ct\), decryption involves computing \(\) and seeing if it's closer to \(0\) or \(\frac\). This "perspective" is much more robust to certain kinds of errors, where you know the error is small but can't guarantee that it's a multiple of 2.Now, here is something we can do to a ciphertext.Start: \( = \ + 2e\ (mod\ p)\) Divide \(ct\) by 2 (modulo \(p\)): \( = \ + 2e' + 2e_2\ (mod\ q)\) Step 3 is the crucial one: it converts a ciphertext under modulus \(p\) into a ciphertext under modulus \(q\). The process just involves "scaling down" each element of \(ct'\) by multiplying by \(\frac\) and rounding down, eg. \(floor(56 * \frac) = floor(8.15533..) = 8\).The idea is this: if \( = p(z + \frac) + e\) for some integer \(z\). Therefore, \( = m*\frac + e' + e_2\ (mod\ q)\), where \(e' = e * \frac\), and \(e_2\) is a small error from rounding.What have we accomplished? We turned a ciphertext with modulus \(p\) and error \(2e\) into a ciphertext with modulus \(q\) and error \(2(floor(e*\frac) + e_2)\), where the new error is smaller than the original error.Let's go through the above with an example. Suppose:\(ct\) is just one value, \([5612]\) \(k = [9]\) \(p = 9999\) and \(q = 113\) \( = 5612 * 9 = 50508 = 9999 * 5 + 2 * 256 + 1\), so \(ct\) represents the bit 1, but the error is fairly large (\(e = 256\)).Step 2: \(ct' = \frac = 2806\) (remember this is modular division; if \(ct\) were instead \(5613\), then we would have \(\frac = 7806\)). Checking: \(
Exploring Fully Homomorphic Encryption Exploring Fully Homomorphic Encryption2020 Jul 20 See all posts Exploring Fully Homomorphic Encryption Special thanks to Karl Floersch and Dankrad Feist for reviewFully homomorphic encryption has for a long time been considered one of the holy grails of cryptography. The promise of fully homomorphic encryption (FHE) is powerful: it is a type of encryption that allows a third party to perform computations on encrypted data, and get an encrypted result that they can hand back to whoever has the decryption key for the original data, without the third party being able to decrypt the data or the result themselves. As a simple example, imagine that you have a set of emails, and you want to use a third party spam filter to check whether or not they are spam. The spam filter has a desire for privacy of their algorithm: either the spam filter provider wants to keep their source code closed, or the spam filter depends on a very large database that they do not want to reveal publicly as that would make attacking easier, or both. However, you care about the privacy of your data, and don't want to upload your unencrypted emails to a third party. So here's how you do it: Fully homomorphic encryption has many applications, including in the blockchain space. One key example is that can be used to implement privacy-preserving light clients (the light client hands the server an encrypted index i, the server computes and returns data[0] * (i = 0) + data[1] * (i = 1) + ... + data[n] * (i = n), where data[i] is the i'th piece of data in a block or state along with its Merkle branch and (i = k) is an expression that returns 1 if i = k and otherwise 0; the light client gets the data it needs and the server learns nothing about what the light client asked).It can also be used for:More efficient stealth address protocols, and more generally scalability solutions to privacy-preserving protocols that today require each user to personally scan the entire blockchain for incoming transactions Privacy-preserving data-sharing marketplaces that let users allow some specific computation to be performed on their data while keeping full control of their data for themselves An ingredient in more powerful cryptographic primitives, such as more efficient multi-party computation protocols and perhaps eventually obfuscation And it turns out that fully homomorphic encryption is, conceptually, not that difficult to understand!Partially, Somewhat, Fully homomorphic encryptionFirst, a note on definitions. There are different kinds of homomorphic encryption, some more powerful than others, and they are separated by what kinds of functions one can compute on the encrypted data.Partially homomorphic encryption allows evaluating only a very limited set of operations on encrypted data: either just additions (so given encrypt(a) and encrypt(b) you can compute encrypt(a+b)), or just multiplications (given encrypt(a) and encrypt(b) you can compute encrypt(a*b)). Somewhat homomorphic encryption allows computing additions as well as a limited number of multiplications (alternatively, polynomials up to a limited degree). That is, if you get encrypt(x1) ... encrypt(xn) (assuming these are "original" encryptions and not already the result of homomorphic computation), you can compute encrypt(p(x1 ... xn)), as long as p(x1 ... xn) is a polynomial with degree < D for some specific degree bound D (D is usually very low, think 5-15). Fully homomorphic encryption allows unlimited additions and multiplications. Additions and multiplications let you replicate any binary circuit gates (AND(x, y) = x*y, OR(x, y) = x+y-x*y, XOR(x, y) = x+y-2*x*y or just x+y if you only care about even vs odd, NOT(x) = 1-x...), so this is sufficient to do arbitrary computation on encrypted data. Partially homomorphic encryption is fairly easy; eg. RSA has a multiplicative homomorphism: \(enc(x) = x^e\), \(enc(y) = y^e\), so \(enc(x) * enc(y) = (xy)^e = enc(xy)\). Elliptic curves can offer similar properties with addition. Allowing both addition and multiplication is, it turns out, significantly harder.A simple somewhat-HE algorithmHere, we will go through a somewhat-homomorphic encryption algorithm (ie. one that supports a limited number of multiplications) that is surprisingly simple. A more complex version of this category of technique was used by Craig Gentry to create the first-ever fully homomorphic scheme in 2009. More recent efforts have switched to using different schemes based on vectors and matrices, but we will still go through this technique first.We will describe all of these encryption schemes as secret-key schemes; that is, the same key is used to encrypt and decrypt. Any secret-key HE scheme can be turned into a public key scheme easily: a "public key" is typically just a set of many encryptions of zero, as well as an encryption of one (and possibly more powers of two). To encrypt a value, generate it by adding together the appropriate subset of the non-zero encryptions, and then adding a random subset of the encryptions of zero to "randomize" the ciphertext and make it infeasible to tell what it represents.The secret key here is a large prime, \(p\) (think of \(p\) as having hundreds or even thousands of digits). The scheme can only encrypt 0 or 1, and "addition" becomes XOR, ie. 1 + 1 = 0. To encrypt a value \(m\) (which is either 0 or 1), generate a large random value \(R\) (this will typically be even larger than \(p\)) and a smaller random value \(r\) (typically much smaller than \(p\)), and output:\[enc(m) = R * p + r * 2 + m\]To decrypt a ciphertext \(ct\), compute:\[dec(ct) = (ct\ mod\ p)\ mod\ 2\]To add two ciphertexts \(ct_1\) and \(ct_2\), you simply, well, add them: \(ct_1 + ct_2\). And to multiply two ciphertexts, you once again... multiply them: \(ct_1 * ct_2\). We can prove the homomorphic property (that the sum of the encryptions is an encryption of the sum, and likewise for products) as follows.Let:\[ct_1 = R_1 * p + r_1 * 2 + m_1\] \[ct_2 = R_2 * p + r_2 * 2 + m_2\]We add:\[ct_1 + ct_2 = R_1 * p + R_2 * p + r_1 * 2 + r_2 * 2 + m_1 + m_2\]Which can be rewritten as:\[(R_1 + R_2) * p + (r_1 + r_2) * 2 + (m_1 + m_2)\]Which is of the exact same "form" as a ciphertext of \(m_1 + m_2\). If you decrypt it, the first \(mod\ p\) removes the first term, the second \(mod\ 2\) removes the second term, and what's left is \(m_1 + m_2\) (remember that if \(m_1 = 1\) and \(m_2 = 1\) then the 2 will get absorbed into the second term and you'll be left with zero). And so, voila, we have additive homomorphism!Now let's check multiplication:\[ct_1 * ct_2 = (R_1 * p + r_1 * 2 + m_1) * (R_2 * p + r_2 * 2 + m_2)\]Or:\[(R_1 * R_2 * p + r_1 * 2 + m_1 + r_2 * 2 + m_2) * p + \] \[(r_1 * r_2 * 2 + r_1 * m_2 + r_2 * m_1) * 2 + \] \[(m_1 * m_2)\]This was simply a matter of expanding the product above, and grouping together all the terms that contain \(p\), then all the remaining terms that contain \(2\), and finally the remaining term which is the product of the messages. If you decrypt, then once again the \(mod\ p\) removes the first group, the \(mod\ 2\) removes the second group, and only \(m_1 * m_2\) is left.But there are two problems here: first, the size of the ciphertext itself grows (the length roughly doubles when you multiply), and second, the "noise" (also often called "error") in the smaller \(\* 2\) term also gets quadratically bigger. Adding this error into the ciphertexts was necessary because the security of this scheme is based on the approximate GCD problem: Had we instead used the "exact GCD problem", breaking the system would be easy: if you just had a set of expressions of the form \(p * R_1 + m_1\), \(p * R_2 + m_2\)..., then you could use the Euclidean algorithm to efficiently compute the greatest common divisor \(p\). But if the ciphertexts are only approximate multiples of \(p\) with some "error", then extracting \(p\) quickly becomes impractical, and so the scheme can be secure.Unfortunately, the error introduces the inherent limitation that if you multiply the ciphertexts by each other enough times, the error eventually grows big enough that it exceeds \(p\), and at that point the \(mod\ p\) and \(mod\ 2\) steps "interfere" with each other, making the data unextractable. This will be an inherent tradeoff in all of these homomorphic encryption schemes: extracting information from approximate equations "with errors" is much harder than extracting information from exact equations, but any error you add quickly increases as you do computations on encrypted data, bounding the amount of computation that you can do before the error becomes overwhelming. And this is why these schemes are only "somewhat" homomorphic.BootstrappingThere are two classes of solution to this problem. First, in many somewhat homomorphic encryption schemes, there are clever tricks to make multiplication only increase the error by a constant factor (eg. 1000x) instead of squaring it. Increasing the error by 1000x still sounds by a lot, but keep in mind that if \(p\) (or its equivalent in other schemes) is a 300-digit number, that means that you can multiply numbers by each other 100 times, which is enough to compute a very wide class of computations. Second, there is Craig Gentry's technique of "bootstrapping".Suppose that you have a ciphertext \(ct\) that is an encryption of some \(m\) under a key \(p\), that has a lot of error. The idea is that we "refresh" the ciphertext by turning it into a new ciphertext of \(m\) under another key \(p_2\), where this process "clears out" the old error (though it will introduce a fixed amount of new error). The trick is quite clever. The holder of \(p\) and \(p_2\) provides a "bootstrapping key" that consists of an encryption of the bits of \(p\) under the key \(p_2\), as well as the public key for \(p_2\). Whoever is doing computations on data encrypted under \(p\) would then take the bits of the ciphertext \(ct\), and individually encrypt these bits under \(p_2\). They would then homomorphically compute the decryption under \(p\) using these ciphertexts, and get out the single bit, which would be \(m\) encrypted under \(p_2\). This is difficult to understand, so we can restate it as follows. The decryption procedure \(dec(ct, p)\) is itself a computation, and so it can itself be implemented as a circuit that takes as input the bits of \(ct\) and the bits of \(p\), and outputs the decrypted bit \(m \in \). If someone has a ciphertext \(ct\) encrypted under \(p\), a public key for \(p_2\), and the bits of \(p\) encrypted under \(p_2\), then they can compute \(dec(ct, p) = m\) "homomorphically", and get out \(m\) encrypted under \(p_2\). Notice that the decryption procedure itself washes away the old error; it just outputs 0 or 1. The decryption procedure is itself a circuit, which contains additions or multiplications, so it will introduce new error, but this new error does not depend on the amount of error in the original encryption.(Note that we can avoid having a distinct new key \(p_2\) (and if you want to bootstrap multiple times, also a \(p_3\), \(p_4\)...) by just setting \(p_2 = p\). However, this introduces a new assumption, usually called "circular security"; it becomes more difficult to formally prove security if you do this, though many cryptographers think it's fine and circular security poses no significant risk in practice)But.... there is a catch. In the scheme as described above (using circular security or not), the error blows up so quickly that even the decryption circuit of the scheme itself is too much for it. That is, the new \(m\) encrypted under \(p_2\) would already have so much error that it is unreadable. This is because each AND gate doubles the bit-length of the error, so a scheme using a \(d\)-bit modulus \(p\) can only handle less than \(log(d)\) multiplications (in series), but decryption requires computing \(mod\ p\) in a circuit made up of these binary logic gates, which requires... more than \(log(d)\) multiplications.Craig Gentry came up with clever techniques to get around this problem, but they are arguably too complicated to explain; instead, we will skip straight to newer work from 2011 and 2013, that solves this problem in a different way.Learning with errorsTo move further, we will introduce a different type of somewhat-homomorphic encryption introduced by Brakerski and Vaikuntanathan in 2011, and show how to bootstrap it. Here, we will move away from keys and ciphertexts being integers, and instead have keys and ciphertexts be vectors. Given a key \(k = \), to encrypt a message \(m\), construct a vector \(c = \) such that the inner product (or "dot product") \( = c_1k_1 + c_2k_1 + ... + c_nk_n\), modulo some fixed number \(p\), equals \(m+2e\) where \(m\) is the message (which must be 0 or 1), and \(e\) is a small (much smaller than \(p\)) "error" term. A "public key" that allows encryption but not decryption can be constructed, as before, by making a set of encryptions of 0; an encryptor can randomly combine a subset of these equations and add 1 if the message they are encrypting is 1. To decrypt a ciphertext \(c\) knowing the key \(k\), you would compute \(\) modulo \(p\), and see if the result is odd or even (this is the same "mod p mod 2" trick we used earlier). Note that here the \(mod\ p\) is typically a "symmetric" mod, that is, it returns a number between \(-\frac\) and \(\frac\) (eg. 137 mod 10 = -3, 212 mod 10 = 2); this allows our error to be positive or negative. Additionally, \(p\) does not necessarily have to be prime, though it does need to be odd. Key 3 14 15 92 65 Ciphertext 2 71 82 81 8 The key and the ciphertext are both vectors, in this example of five elements each.In this example, we set the modulus \(p = 103\). The dot product is 3 * 2 + 14 * 71 + 15 * 82 + 92 * 81 + 65 * 8 = 10202, and \(10202 = 99 * 103 + 5\). 5 itself is of course \(2 * 2 + 1\), so the message is 1. Note that in practice, the first element of the key is often set to \(1\); this makes it easier to generate ciphertexts for a particular value (see if you can figure out why).The security of the scheme is based on an assumption known as "learning with errors" (LWE) - or, in more jargony but also more understandable terms, the hardness of solving systems of equations with errors. A ciphertext can itself be viewed as an equation: \(k_1c_1 + .... + k_nc_n \approx 0\), where the key \(k_1 ... k_n\) is the unknowns, the ciphertext \(c_1 ... c_n\) is the coefficients, and the equality is only approximate because of both the message (0 or 1) and the error (\(2e\) for some relatively small \(e\)). The LWE assumption ensures that even if you have access to many of these ciphertexts, you cannot recover \(k\).Note that in some descriptions of LWE, can equal any value, but this value must be provided as part of the ciphertext. This is mathematically equivalent to the = m+2e formulation, because you can just add this answer to the end of the ciphertext and add -1 to the end of the key, and get two vectors that when multiplied together just give m+2e. We'll use the formulation that requires to be near-zero (ie. just m+2e) because it is simpler to work with.Multiplying ciphertextsIt is easy to verify that the encryption is additive: if \( = 2e_1 + m_1\) and \( = 2e_2 + m_2\), then \( = 2(e_1 + e_2) + m_1 + m_2\) (the addition here is modulo \(p\)). What is harder is multiplication: unlike with numbers, there is no natural way to multiply two length-n vectors into another length-n vector. The best that we can do is the outer product: a vector containing the products of each possible pair where the first element comes from the first vector and the second element comes from the second vector. That is, \(a \otimes b = a_1b_1 + a_2b_1 + ... + a_nb_1 + a_1b_2 + ... + a_nb_2 + ... + a_nb_n\). We can "multiply ciphertexts" using the convenient mathematical identity \( = * \).Given two ciphertexts \(c_1\) and \(c_2\), we compute the outer product \(c_1 \otimes c_2\). If both \(c_1\) and \(c_2\) were encrypted with \(k\), then \( = 2e_1 + m_1\) and \( = 2e_2 + m_2\). The outer product \(c_1 \otimes c_2\) can be viewed as an encryption of \(m_1 * m_2\) under \(k \otimes k\); we can see this by looking what happens when we try to decrypt with \(k \otimes k\):\[\] \[= * \] \[ = (2e_1 + m_1) * (2e_2 + m_2)\] \[ = 2(e_1m_2 + e_2m_1 + 2e_1e_2) + m_1m_2\]So this outer-product approach works. But there is, as you may have already noticed, a catch: the size of the ciphertext, and the key, grows quadratically.RelinearizationWe solve this with a relinearization procedure. The holder of the private key \(k\) provides, as part of the public key, a "relinearization key", which you can think of as "noisy" encryptions of \(k \otimes k\) under \(k\). The idea is that we provide these encrypted pieces of \(k \otimes k\) to anyone performing the computations, allowing them to compute the equation \(\) to "decrypt" the ciphertext, but only in such a way that the output comes back encrypted under \(k\).It's important to understand what we mean here by "noisy encryptions". Normally, this encryption scheme only allows encrypting \(m \in \\), and an "encryption of \(m\)" is a vector \(c\) such that \( = m+2e\) for some small error \(e\). Here, we're "encrypting" arbitrary \(m \in \\). Note that the error means that you can't fully recover \(m\) from \(c\); your answer will be off by some multiple of 2. However, it turns out that, for this specific use case, this is fine.The relinearization key consists of a set of vectors which, when inner-producted (modulo \(p\)) with the key \(k\), give values of the form \(k_i * k_j * 2^d + 2e\) (mod \(p\)), one such vector for every possible triple \((i, j, d)\), where \(i\) and \(j\) are indices in the key and \(d\) is an exponent where \(2^d < p\) (note: if the key has length \(n\), there would be \(n^2 * log(p)\) values in the relinearization key; make sure you understand why before continuing). Example assuming p = 15 and k has length 2. Formally, enc(x) here means "outputs x+2e if inner-producted with k".Now, let us take a step back and look again at our goal. We have a ciphertext which, if decrypted with \(k \otimes k\), gives \(m_1 * m_2\). We want a ciphertext which, if decrypted with \(k\), gives \(m_1 * m_2\). We can do this with the relinearization key. Notice that the decryption equation \(\) is just a big sum of terms of the form \((ct_ * ct_) * k_p * k_q\).And what do we have in our relinearization key? A bunch of elements of the form \(2^d * k_p * k_q\), noisy-encrypted under \(k\), for every possible combination of \(p\) and \(q\)! Having all the powers of two in our relinearization key allows us to generate any \((ct_ * ct_) * k_p * k_q\) by just adding up \(\le log(p)\) powers of two (eg. 13 = 8 + 4 + 1) together for each \((p, q)\) pair.For example, if \(ct_1 = [1, 2]\) and \(ct_2 = [3, 4]\), then \(ct_1 \otimes ct_2 = [3, 4, 6, 8]\), and \(enc() = enc(3k_1k_1 + 4k_1k_2 + 6k_2k_1 + 8k_2k_2)\) could be computed via:\[enc(k_1 * k_1) + enc(k_1 * k_1 * 2) + enc(k_1 * k_2 * 4) + \]\[enc(k_2 * k_1 * 2) + enc(k_2 * k_1 * 4) + enc(k_2 * k_2 * 8) \]Note that each noisy-encryption in the relinearization key has some even error \(2e\), and the equation \(\) itself has some error: if \( = 2e_1 + m_1\) and \( = 2e_2 + m_2\), then \( =\) \( * =\) \(2(2e_1e_2 + e_1m_2 + e_2m_1) + m_1m_2\). But this total error is still (relatively) small (\(2e_1e_2 + e_1m_2 + e_2m_1\) plus \(n^2 * log(p)\) fixed-size errors from the realinearization key), and the error is even, and so the result of this calculation still gives a value which, when inner-producted with \(k\), gives \(m_1 * m_2 + 2e'\) for some "combined error" \(e'\).The broader technique we used here is a common trick in homomorphic encryption: provide pieces of the key encrypted under the key itself (or a different key if you are pedantic about avoiding circular security assumptions), such that someone computing on the data can compute the decryption equation, but only in such a way that the output itself is still encrypted. It was used in bootstrapping above, and it's used here; it's best to make sure you mentally understand what's going on in both cases.This new ciphertext has considerably more error in it: the \(n^2 * log(p)\) different errors from the portions of the relinearization key that we used, plus the \(2(2e_1e_2 + e_1m_2 + e_2m_1)\) from the original outer-product ciphertext. Hence, the new ciphertext still does have quadratically larger error than the original ciphertexts, and so we still haven't solved the problem that the error blows up too quickly. To solve this, we move on to another trick...Modulus switchingHere, we need to understand an important algebraic fact. A ciphertext is a vector \(ct\), such that \( = m+2e\), where \(m \in \\). But we can also look at the ciphertext from a different "perspective": consider \(\frac\) (modulo \(p\)). \( = \frac + e\), where \(\frac \in \\}\). Note that because (modulo \(p\)) \((\frac)*2 = p+1 = 1\), division by 2 (modulo \(p\)) maps \(1\) to \(\frac\); this is a very convenient fact for us. The scheme in this section uses both modular division (ie. multiplying by the modular multiplicative inverse) and regular "rounded down" integer division; make sure you understand how both work and how they are different from each other.That is, the operation of dividing by 2 (modulo \(p\)) converts small even numbers into small numbers, and it converts 1 into \(\frac\) (rounded up). So if we look at \(\frac\) (modulo \(p\)) instead of \(ct\), decryption involves computing \(\) and seeing if it's closer to \(0\) or \(\frac\). This "perspective" is much more robust to certain kinds of errors, where you know the error is small but can't guarantee that it's a multiple of 2.Now, here is something we can do to a ciphertext.Start: \( = \ + 2e\ (mod\ p)\) Divide \(ct\) by 2 (modulo \(p\)): \( = \ + 2e' + 2e_2\ (mod\ q)\) Step 3 is the crucial one: it converts a ciphertext under modulus \(p\) into a ciphertext under modulus \(q\). The process just involves "scaling down" each element of \(ct'\) by multiplying by \(\frac\) and rounding down, eg. \(floor(56 * \frac) = floor(8.15533..) = 8\).The idea is this: if \( = p(z + \frac) + e\) for some integer \(z\). Therefore, \( = m*\frac + e' + e_2\ (mod\ q)\), where \(e' = e * \frac\), and \(e_2\) is a small error from rounding.What have we accomplished? We turned a ciphertext with modulus \(p\) and error \(2e\) into a ciphertext with modulus \(q\) and error \(2(floor(e*\frac) + e_2)\), where the new error is smaller than the original error.Let's go through the above with an example. Suppose:\(ct\) is just one value, \([5612]\) \(k = [9]\) \(p = 9999\) and \(q = 113\) \( = 5612 * 9 = 50508 = 9999 * 5 + 2 * 256 + 1\), so \(ct\) represents the bit 1, but the error is fairly large (\(e = 256\)).Step 2: \(ct' = \frac = 2806\) (remember this is modular division; if \(ct\) were instead \(5613\), then we would have \(\frac = 7806\)). Checking: \( -
 Base Layers And Functionality Escape Velocity Base Layers And Functionality Escape Velocity2019 Dec 26 See all posts Base Layers And Functionality Escape Velocity One common strand of thinking in blockchain land goes as follows: blockchains should be maximally simple, because they are a piece of infrastructure that is difficult to change and would lead to great harms if it breaks, and more complex functionality should be built on top, in the form of layer 2 protocols: state channels, Plasma, rollup, and so forth. Layer 2 should be the site of ongoing innovation, layer 1 should be the site of stability and maintenance, with large changes only in emergencies (eg. a one-time set of serious breaking changes to prevent the base protocol's cryptography from falling to quantum computers would be okay).This kind of layer separation is a very nice idea, and in the long term I strongly support this idea. However, this kind of thinking misses an important point: while layer 1 cannot be too powerful, as greater power implies greater complexity and hence greater brittleness, layer 1 must also be powerful enough for the layer 2 protocols-on-top that people want to build to actually be possible in the first place. Once a layer 1 protocol has achieved a certain level of functionality, which I will term "functionality escape velocity", then yes, you can do everything else on top without further changing the base. But if layer 1 is not powerful enough, then you can talk about filling in the gap with layer 2 systems, but the reality is that there is no way to actually build those systems, without reintroducing a whole set of trust assumptions that the layer 1 was trying to get away from. This post will talk about some of what this minimal functionality that constitutes "functionality escape velocity" is.A programming languageIt must be possible to execute custom user-generated scripts on-chain. This programming language can be simple, and actually does not need to be high-performance, but it needs to at least have the level of functionality required to be able to verify arbitrary things that might need to be verified. This is important because the layer 2 protocols that are going to be built on top need to have some kind of verification logic, and this verification logic must be executed by the blockchain somehow.You may have heard of Turing completeness; the "layman's intuition" for the term being that if a programming language is Turing complete then it can do anything that a computer theoretically could do. Any program in one Turing-complete language can be translated into an equivalent program in any other Turing-complete language. However, it turns out that we only need something slightly lighter: it's okay to restrict to programs without loops, or programs which are guaranteed to terminate in a specific number of steps.Rich StatefulnessIt doesn't just matter that a programming language exists, it also matters precisely how that programming language is integrated into the blockchain. Among the more constricted ways that a language could be integrated is if it is used for pure transaction verification: when you send coins to some address, that address represents a computer program P which would be used to verify a transaction that sends coins from that address. That is, if you send a transaction whose hash is h, then you would supply a signature S, and the blockchain would run P(h, S), and if that outputs TRUE then the transaction is valid. Often, P is a verifier for a cryptographic signature scheme, but it could do more complex operations. Note particularly that in this model P does not have access to the destination of the transaction.However, this "pure function" approach is not enough. This is because this pure function-based approach is not powerful enough to implement many kinds of layer 2 protocols that people actually want to implement. It can do channels (and channel-based systems like the Lightning Network), but it cannot implement other scaling techniques with stronger properties, it cannot be used to bootstrap systems that do have more complicated notions of state, and so forth.To give a simple example of what the pure function paradigm cannot do, consider a savings account with the following feature: there is a cryptographic key k which can initiate a withdrawal, and if a withdrawal is initiated, within the next 24 hours that same key k can cancel the withdrawal. If a withdrawal remains uncancelled within 24 hours, then anyone can "poke" the account to finalize that withdrawal. The goal is that if the key is stolen, the account holder can prevent the thief from withdrawing the funds. The thief could of course prevent the legitimate owner from getting the funds, but the attack would not be profitable for the thief and so they would probably not bother with it (see the original paper for an explanation of this technique).Unfortunately this technique cannot be implemented with just pure functions. The problem is this: there needs to be some way to move coins from a "normal" state to an "awaiting withdrawal" state. But the program P does not have access to the destination! Hence, any transaction that could authorize moving the coins to an awaiting withdrawal state could also authorize just stealing those coins immediately; P can't tell the difference. The ability to change the state of coins, without completely setting them free, is important to many kinds of applications, including layer 2 protocols. Plasma itself fits into this "authorize, finalize, cancel" paradigm: an exit from Plasma must be approved, then there is a 7 day challenge period, and within that challenge period the exit could be cancelled if the right evidence is provided. Rollup also needs this property: coins inside a rollup must be controlled by a program that keeps track of a state root R, and changes from R to R' if some verifier P(R, R', data) returns TRUE - but it only changes the state to R' in that case, it does not set the coins free.This ability to authorize state changes without completely setting all coins in an account free, is what I mean by "rich statefulness". It can be implemented in many ways, some UTXO-based, but without it a blockchain is not powerful enough to implement most layer 2 protocols, without including trust assumptions (eg. a set of functionaries who are collectively trusted to execute those richly-stateful programs).Note: yes, I know that if P has access to h then you can just include the destination address as part of S and check it against h, and restrict state changes that way. But it is possible to have a programming language that is too resource-limited or otherwise restricted to actually do this; and surprisingly this often actually is the case in blockchain scripting languages.Sufficient data scalability and low latencyIt turns out that plasma and channels, and other layer 2 protocols that are fully off-chain have some fundamental weaknesses that prevent them from fully replicating the capabilities of layer 1. I go into this in detail here; the summary is that these protocols need to have a way of adjudicating situations where some parties maliciously fail to provide data that they promised to provide, and because data publication is not globally verifiable (you don't know when data was published unless you already downloaded it yourself) these adjudication games are not game-theoretically stable. Channels and Plasma cleverly get around this instability by adding additional assumptions, particularly assuming that for every piece of state, there is a single actor that is interested in that state not being incorrectly modified (usually because it represents coins that they own) and so can be trusted to fight on its behalf. However, this is far from general-purpose; systems like Uniswap, for example, include a large "central" contract that is not owned by anyone, and so they cannot effectively be protected by this paradigm.There is one way to get around this, which is layer 2 protocols that publish very small amounts of data on-chain, but do computation entirely off-chain. If data is guaranteed to be available, then computation being done off-chain is okay, because games for adjudicating who did computation correctly and who did it incorrectly are game-theoretically stable (or could be replaced entirely by SNARKs or STARKs). This is the logic behind ZK rollup and optimistic rollup. If a blockchain allows for the publication and guarantees the availability of a reasonably large amount of data, even if its capacity for computation remains very limited, then the blockchain can support these layer-2 protocols and achieve a high level of scalability and functionality.Just how much data does the blockchain need to be able to process and guarantee? Well, it depends on what TPS you want. With a rollup, you can compress most activity to ~10-20 bytes per transaction, so 1 kB/sec gives you 50-100 TPS, 1 MB/sec gives you 50,000-100,000 TPS, and so forth. Fortunately, internet bandwidth continues to grow quickly, and does not seem to be slowing down the way Moore's law for computation is, so increasing scaling for data without increasing computational load is quite a viable path for blockchains to take!Note also that it is not just data capacity that matters, it is also data latency (ie. having low block times). Layer 2 protocols like rollup (or for that matter Plasma) only give any guarantees of security when the data actually is published to chain; hence, the time it takes for data to be reliably included (ideally "finalized") on chain is the time that it takes between when Alice sends Bob a payment and Bob can be confident that this payment will be included. The block time of the base layer sets the latency for anything whose confirmation depends things being included in the base layer. This could be worked around with on-chain security deposits, aka "bonds", at the cost of high capital inefficiency, but such an approach is inherently imperfect because a malicious actor could trick an unlimited number of different people by sacrificing one deposit.Conclusions"Keep layer 1 simple, make up for it on layer 2" is NOT a universal answer to blockchain scalability and functionality problems, because it fails to take into account that layer 1 blockchains themselves must have a sufficient level of scalability and functionality for this "building on top" to actually be possible (unless your so-called "layer 2 protocols" are just trusted intermediaries). However, it is true that beyond a certain point, any layer 1 functionality can be replicated on layer 2, and in many cases it's a good idea to do this to improve upgradeability. Hence, we need layer 1 development in parallel with layer 2 development in the short term, and more focus on layer 2 in the long term.
Base Layers And Functionality Escape Velocity Base Layers And Functionality Escape Velocity2019 Dec 26 See all posts Base Layers And Functionality Escape Velocity One common strand of thinking in blockchain land goes as follows: blockchains should be maximally simple, because they are a piece of infrastructure that is difficult to change and would lead to great harms if it breaks, and more complex functionality should be built on top, in the form of layer 2 protocols: state channels, Plasma, rollup, and so forth. Layer 2 should be the site of ongoing innovation, layer 1 should be the site of stability and maintenance, with large changes only in emergencies (eg. a one-time set of serious breaking changes to prevent the base protocol's cryptography from falling to quantum computers would be okay).This kind of layer separation is a very nice idea, and in the long term I strongly support this idea. However, this kind of thinking misses an important point: while layer 1 cannot be too powerful, as greater power implies greater complexity and hence greater brittleness, layer 1 must also be powerful enough for the layer 2 protocols-on-top that people want to build to actually be possible in the first place. Once a layer 1 protocol has achieved a certain level of functionality, which I will term "functionality escape velocity", then yes, you can do everything else on top without further changing the base. But if layer 1 is not powerful enough, then you can talk about filling in the gap with layer 2 systems, but the reality is that there is no way to actually build those systems, without reintroducing a whole set of trust assumptions that the layer 1 was trying to get away from. This post will talk about some of what this minimal functionality that constitutes "functionality escape velocity" is.A programming languageIt must be possible to execute custom user-generated scripts on-chain. This programming language can be simple, and actually does not need to be high-performance, but it needs to at least have the level of functionality required to be able to verify arbitrary things that might need to be verified. This is important because the layer 2 protocols that are going to be built on top need to have some kind of verification logic, and this verification logic must be executed by the blockchain somehow.You may have heard of Turing completeness; the "layman's intuition" for the term being that if a programming language is Turing complete then it can do anything that a computer theoretically could do. Any program in one Turing-complete language can be translated into an equivalent program in any other Turing-complete language. However, it turns out that we only need something slightly lighter: it's okay to restrict to programs without loops, or programs which are guaranteed to terminate in a specific number of steps.Rich StatefulnessIt doesn't just matter that a programming language exists, it also matters precisely how that programming language is integrated into the blockchain. Among the more constricted ways that a language could be integrated is if it is used for pure transaction verification: when you send coins to some address, that address represents a computer program P which would be used to verify a transaction that sends coins from that address. That is, if you send a transaction whose hash is h, then you would supply a signature S, and the blockchain would run P(h, S), and if that outputs TRUE then the transaction is valid. Often, P is a verifier for a cryptographic signature scheme, but it could do more complex operations. Note particularly that in this model P does not have access to the destination of the transaction.However, this "pure function" approach is not enough. This is because this pure function-based approach is not powerful enough to implement many kinds of layer 2 protocols that people actually want to implement. It can do channels (and channel-based systems like the Lightning Network), but it cannot implement other scaling techniques with stronger properties, it cannot be used to bootstrap systems that do have more complicated notions of state, and so forth.To give a simple example of what the pure function paradigm cannot do, consider a savings account with the following feature: there is a cryptographic key k which can initiate a withdrawal, and if a withdrawal is initiated, within the next 24 hours that same key k can cancel the withdrawal. If a withdrawal remains uncancelled within 24 hours, then anyone can "poke" the account to finalize that withdrawal. The goal is that if the key is stolen, the account holder can prevent the thief from withdrawing the funds. The thief could of course prevent the legitimate owner from getting the funds, but the attack would not be profitable for the thief and so they would probably not bother with it (see the original paper for an explanation of this technique).Unfortunately this technique cannot be implemented with just pure functions. The problem is this: there needs to be some way to move coins from a "normal" state to an "awaiting withdrawal" state. But the program P does not have access to the destination! Hence, any transaction that could authorize moving the coins to an awaiting withdrawal state could also authorize just stealing those coins immediately; P can't tell the difference. The ability to change the state of coins, without completely setting them free, is important to many kinds of applications, including layer 2 protocols. Plasma itself fits into this "authorize, finalize, cancel" paradigm: an exit from Plasma must be approved, then there is a 7 day challenge period, and within that challenge period the exit could be cancelled if the right evidence is provided. Rollup also needs this property: coins inside a rollup must be controlled by a program that keeps track of a state root R, and changes from R to R' if some verifier P(R, R', data) returns TRUE - but it only changes the state to R' in that case, it does not set the coins free.This ability to authorize state changes without completely setting all coins in an account free, is what I mean by "rich statefulness". It can be implemented in many ways, some UTXO-based, but without it a blockchain is not powerful enough to implement most layer 2 protocols, without including trust assumptions (eg. a set of functionaries who are collectively trusted to execute those richly-stateful programs).Note: yes, I know that if P has access to h then you can just include the destination address as part of S and check it against h, and restrict state changes that way. But it is possible to have a programming language that is too resource-limited or otherwise restricted to actually do this; and surprisingly this often actually is the case in blockchain scripting languages.Sufficient data scalability and low latencyIt turns out that plasma and channels, and other layer 2 protocols that are fully off-chain have some fundamental weaknesses that prevent them from fully replicating the capabilities of layer 1. I go into this in detail here; the summary is that these protocols need to have a way of adjudicating situations where some parties maliciously fail to provide data that they promised to provide, and because data publication is not globally verifiable (you don't know when data was published unless you already downloaded it yourself) these adjudication games are not game-theoretically stable. Channels and Plasma cleverly get around this instability by adding additional assumptions, particularly assuming that for every piece of state, there is a single actor that is interested in that state not being incorrectly modified (usually because it represents coins that they own) and so can be trusted to fight on its behalf. However, this is far from general-purpose; systems like Uniswap, for example, include a large "central" contract that is not owned by anyone, and so they cannot effectively be protected by this paradigm.There is one way to get around this, which is layer 2 protocols that publish very small amounts of data on-chain, but do computation entirely off-chain. If data is guaranteed to be available, then computation being done off-chain is okay, because games for adjudicating who did computation correctly and who did it incorrectly are game-theoretically stable (or could be replaced entirely by SNARKs or STARKs). This is the logic behind ZK rollup and optimistic rollup. If a blockchain allows for the publication and guarantees the availability of a reasonably large amount of data, even if its capacity for computation remains very limited, then the blockchain can support these layer-2 protocols and achieve a high level of scalability and functionality.Just how much data does the blockchain need to be able to process and guarantee? Well, it depends on what TPS you want. With a rollup, you can compress most activity to ~10-20 bytes per transaction, so 1 kB/sec gives you 50-100 TPS, 1 MB/sec gives you 50,000-100,000 TPS, and so forth. Fortunately, internet bandwidth continues to grow quickly, and does not seem to be slowing down the way Moore's law for computation is, so increasing scaling for data without increasing computational load is quite a viable path for blockchains to take!Note also that it is not just data capacity that matters, it is also data latency (ie. having low block times). Layer 2 protocols like rollup (or for that matter Plasma) only give any guarantees of security when the data actually is published to chain; hence, the time it takes for data to be reliably included (ideally "finalized") on chain is the time that it takes between when Alice sends Bob a payment and Bob can be confident that this payment will be included. The block time of the base layer sets the latency for anything whose confirmation depends things being included in the base layer. This could be worked around with on-chain security deposits, aka "bonds", at the cost of high capital inefficiency, but such an approach is inherently imperfect because a malicious actor could trick an unlimited number of different people by sacrificing one deposit.Conclusions"Keep layer 1 simple, make up for it on layer 2" is NOT a universal answer to blockchain scalability and functionality problems, because it fails to take into account that layer 1 blockchains themselves must have a sufficient level of scalability and functionality for this "building on top" to actually be possible (unless your so-called "layer 2 protocols" are just trusted intermediaries). However, it is true that beyond a certain point, any layer 1 functionality can be replicated on layer 2, and in many cases it's a good idea to do this to improve upgradeability. Hence, we need layer 1 development in parallel with layer 2 development in the short term, and more focus on layer 2 in the long term. -
 Review of Gitcoin Quadratic Funding Round 4 Review of Gitcoin Quadratic Funding Round 42020 Jan 28 See all posts Review of Gitcoin Quadratic Funding Round 4 Round 4 of Gitcoin Grants quadratic funding has just completed, and here are the results: The main distinction between round 3 and round 4 was that while round 3 had only one category, with mostly tech projects and a few outliers such as EthHub, in round 4 there were two separate categories, one with a $125,000 matching pool for tech projects, and the other with a $75,000 matching pool for "media" projects. Media could include documentation, translation, community activities, news reporting, theoretically pretty much anything in that category. And while the tech section went about largely without incident, in the new media section the results proved to be much more interesting than I could have possibly imagined, shedding a new light on deep questions in institutional design and political science.Tech: quadratic funding worked great as usualIn the tech section, the main changes that we see compared to round 3 are (i) the rise of Tornado Cash and (ii) the decline in importance of eth2 clients and the rise of "utility applications" of various forms. Tornado Cash is a trustless smart contract-based Ethereum mixer. It became popular quickly in recent months, as the Ethereum community was swept by worries about the blockchain's current low levels of privacy and wanted solutions. Tornado Cash amassed an incredible $31,200. If they continue receiving such an amount every two months then this would allow them to pay two people $7,800 per month each - meaning that the hoped-for milestone of seeing the first "quadratic freelancer" may have already been reached! The other major winners included tools like Dappnode, a software package to help people run nodes, Sablier, a payment streaming service, and DefiZap, which makes DeFi services easy to use. The Gitcoin Sustainability Fund got over $13,000, conclusively resolving my complaint from last round that they were under-supported. All in all, valuable grants for valuable projects that provide services that the community genuinely needs.We can see one major shift this round compared to the previous rounds. Whereas in previous rounds, the grants went largely to projects like eth2 clients that were already well-supported, this time the largest grants shifted toward having a different focus from the grants given by the Ethereum Foundation. The EF has not given grants to tornado.cash, and generally limits its grants to application-specific tools, Uniswap being a notable exception. The Gitcoin Grants quadratic fund, on the other hand, is supporting DeFiZap, Sablier, and many other tools that are valuable to the community. This is arguably a positive development, as it allows Gitcoin Grants and the Ethereum Foundation to complement each other rather than focusing on the same things.The one proposed change to the quadratic funding implementation for tech that I would favor is a user interface change, that makes it easier for users to commit funds for multiple rounds. This would increase the stability of contributions, thereby increasing the stability of projects' income - very important if we want "quadratic freelancer" to actually be a viable job category!Media: The First Quadratic Twitter FreelancerNow, we get to the new media section. In the first few days of the round, the leading recipient of the grants was "@antiprosynth Twitter account activity": an Ethereum community member who is very active on twitter promoting Ethereum and refuting misinformation from Bitcoin maximalists, asking for help from the Gitcoin QF crowd to.... fund his tweeting activities. At its peak, the projected matching going to @antiprosynth exceeded $20,000. This naturally proved to be controversial, with many criticizing this move and questioning whether or not a Twitter account is a legitimate public good: On the surface, it does indeed seem like someone getting paid $20,000 for operating a Twitter account is ridiculous. But it's worth digging in and questioning exactly what, if anything, is actually wrong with this outcome. After all, maybe this is what effective marketing in 2020 actually looks like, and it's our expectations that need to adapt.There are two main objections that I heard, and both lead to interesting criticisms of quadratic funding in its current implementation. First, there was criticism of overpayment. Twittering is a fairly "trivial" activity; it does not require that much work, lots of people do it for free, and it doesn't provide nearly as much long-term value as something more substantive like EthHub or the Zero Knowledge Podcast. Hence, it feels wrong to pay a full-time salary for it. Examples of @antiprosynth's recent tweetsIf we accept the metaphor of quadratic funding as being like a market for public goods, then one could simply extend the metaphor, and reply to the concern with the usual free-market argument. People voluntarily paid their own money to support @antiprosynth's twitter activity, and that itself signals that it's valuable. Why should we trust you with your mere words and protestations over a costly signal of real money on the table from dozens of people?The most plausible answer is actually quite similar to one that you often hear in discussions about financial markets: markets can give skewed results when you can express an opinion in favor of something but cannot express an opinion against it. When short selling is not possible, financial markets are often much more inefficient, because instead of reflecting the average opinion on an asset's true value, a market may instead reflect the inflated expectations of an asset's few rabid supporters. In this version of quadratic funding, there too is an asymmetry, as you can donate in support of a project but you cannot donate to oppose it. Might this be the root of the problem?One can go further and ask, why might overpayment happen to this particular project, and not others? I have heard a common answer: twitter accounts already have a high exposure. A client development team like Nethermind does not gain much publicity through their work directly, so they need to separately market themselves, whereas a twitter account's "work" is self-marketing by its very nature. Furthermore, the most prominent twitterers get quadratically more matching out of their exposure, amplifying their outsized advantage further - a problem I alluded to in my review of round 3.Interestingly, in the case of vanilla quadratic voting there was an argument made by Glen Weyl for why economies-of-scale effects of traditional voting, such as Duverger's law, don't apply to quadratic voting: a project becoming more prominent increases the incentive to give it both positive and negative votes, so on net the effects cancel out. But notice once again, that this argument relies on negative votes being a possibility.Good for the tribe, but is it good for the world?The particular story of @antiprosynth had what is in my opinion a happy ending: over the next ten days, more contributions came in to other candidates, and @antiprosynth's match reduced to $11,316, still a respectably high amount but on par with EthHub and below Week in Ethereum. However, even a quadratic matching grant of this size still raises to the next criticism: is twittering a public good or public bad anyway?Traditionally, public goods of the type that Gitcoin Grants quadratic funding is trying to support were selected and funded by governments. The motivation of @antiprosynth's tweets is "aggregating Ethereum-related news, fighting information asymmetry and fine-tuning/signaling a consistent narrative for Ethereum (and ETH)": essentially, fighting the good fight against anti-Ethereum misinformation by bitcoin maximalists. And, lo and behold, governments too have a rich history of sponsoring social media participants to argue on their behalf. And it seems likely that most of these governments see themselves as "fighting the good fight against anti-[X] misinformation by [Y] ", just as the Ethereum community feels a need to fight the good fight against maximalist trolls. From the inside view of each individual country (and in our case the Ethereum community) organized social media participation seems to be a clear public good (ignoring the possibility of blowback effects, which are real and important). But from the outside view of the entire world, it can be viewed as a zero-sum game. This is actually a common pattern to see in politics, and indeed there are many instances of larger-scale coordination that are precisely intended to undermine smaller-scale coordination that is seen as "good for the tribe but bad for the world": antitrust law, free trade agreements, state-level pre-emption of local zoning codes, anti-militarization agreements... the list goes on. A broad environment where public subsidies are generally viewed suspiciously also does quite a good job of limiting many kinds of malign local coordination. But as public goods become more important, and we discover better and better ways for communities to coordinate on producing them, that strategy's efficacy becomes more limited, and properly grappling with these discrepancies between what is good for the tribe and what is good for the world becomes more important.That said, internet marketing and debate is not a zero-sum game, and there are plenty of ways to engage in internet marketing and debate that are good for the world. Internet debate in general serves to help the public learn what things are true, what things are not true, what causes to support, and what causes to oppose. Some tactics are clearly not truth-favoring, but other tactics are quite truth-favoring. Some tactics are clearly offensive, but others are defensive. And in the ethereum community, there is widespread sentiment that there is not enough resources going into marketing of some kind, and I personally agree with this sentiment.What kind of marketing is positive-sum (good for tribe and good for world) and what kind of marketing is zero-sum (good for tribe but bad for world) is another question, and one that's worth the community debating. I naturally hope that the Ethereum community continues to value maintaining a moral high ground. Regarding the case of @antiprosynth himself, I cannot find any tactics that I would classify as bad-for-world, especially when compared to outright misinformation ("it's impossible to run a full node") that we often see used against Ethereum - but I am pro-ethereum and hence biased, hence the need to be careful.Universal mechanisms, particular goalsThe story has another plot twist, which reveals yet another feature (or bug?) or quadratic funding. Quadratic funding was originally described as "Formal Rules for a Society Neutral among Communities", the intention being to use it at a very large, potentially even global, scale. Anyone can participate as a project or as a participant, and projects that support public goods that are good for any "public" would be supported. In the case of Gitcoin Grants, however, the matching funds are coming from Ethereum organizations, and so there is an expectation that the system is there to support Ethereum projects. But there is nothing in the rules of quadratic funding that privileges Ethereum projects and prevents, say, Ethereum Classic projects from seeking funding using the same platform! And, of course, this is exactly what happened: So now the result is, $24 of funding from Ethereum organizations will be going toward supporting an Ethereum Classic promoter's twitter activity. To give people outside of the crypto space a feeling for what this is like, imagine the USA holding a quadratic funding raise, using government funding to match donations, and the result is that some of the funding goes to someone explicitly planning to use the money to talk on Twitter about how great Russia is (or vice versa). The matching funds are coming from Ethereum sources, and there's an implied expectation that the funds should support Ethereum, but nothing actually prevents, or even discourages, non-Ethereum projects from organizing to get a share of the matched funds on the platform!SolutionsThere are two solutions to these problems. One is to modify the quadratic funding mechanism to support negative votes in addition to positive votes. The mathematical theory behind quadratic voting already implies that it is the "right thing" to do to allow such a possibility (every positive number has a negative square root as well as a positive square root). On the other hand, there are social concerns that allowing for negative voting would cause more animosity and lead to other kinds of harms. After all, mob mentality is at its worst when it is against something rather than for something. Hence, it's my view that it's not certain that allowing negative contributions will work out well, but there is enough evidence that it might that it is definitely worth trying out in a future round.The second solution is to use two separate mechanisms for identifying relative goodness of good projects and for screening out bad projects. For example, one could use a challenge mechanism followed by a majority ETH coin vote, or even at first just a centralized appointed board, to screen out bad projects, and then use quadratic funding as before to choose between good projects. This is less mathematically elegant, but it would solve the problem, and it would at the same time provide an opportunity to mix in a separate mechanism to ensure that chosen projects benefit Ethereum specifically.But even if we adopt the first solution, defining boundaries for the quadratic funding itself may also be a good idea. There is intellectual precedent for this. In Elinor Ostrom's eight principles for governing the commons, defining clear boundaries about who has the right to access the commons is the first one. Without clear boundaries, Ostrom writes, "local appropriators face the risk that any benefits they produce by their efforts will be reaped by others who have not contributed to those efforts." In the case of Gitcoin Grants quadratic funding, one possibility would be to set the maximum matching coefficient for any pair of users to be proportional to the geometric average of their ETH holdings, using that as a proxy for measuring membership in the Ethereum community (note that this avoids being plutocratic because 1000 users with 1 ETH each would have a maximum matching of \(\approx k * 500,000\) ETH, whereas 2 users with 500 ETH each would only have a maximum matching of \(k * 1,000\) ETH).CollusionAnother issue that came to the forefront this round was the issue of collusion. The math behind quadratic funding, which compensates for tragedies of the commons by magnifying individual contributions based on the total number and size of other contributions to the same project, only works if there is an actual tragedy of the commons limiting natural donations to the project. If there is a "quid pro quo", where people get something individually in exchange for their contributions, the mechanism can easily over-compensate. The long-run solution to this is something like MACI, a cryptographic system that ensures that contributors have no way to prove their contributions to third parties, so any such collusion would have to be done by honor system. In the short run, however, the rules and enforcement has not yet been set, and this has led to vigorous debate about what kinds of quid pro quo are legitimate: [Update 2020.01.29: the above was ultimately a result of a miscommunication from Gitcoin; a member of the Gitcoin team had okayed Richard Burton's proposal to give rewards to donors without realizing the implications. So Richard himself is blameless here; though the broader point that we underestimated the need for explicit guidance about what kinds of quid pro quos are acceptable is very much real.]Currently, the position is that quid pro quos are disallowed, though there is a more nuanced feeling that informal social quid pro quos ("thank yous" of different forms) are okay, whereas formal and especially monetary or product rewards are a no-no. This seems like a reasonable approach, though it does put Gitcoin further into the uncomfortable position of being a central arbiter, compromising credible neutrality somewhat. One positive byproduct of this whole discussion is that it has led to much more awareness in the Ethereum community of what actually is a public good (as opposed to a "private good" or a "club good"), and more generally brought public goods much further into the public discourse.ConclusionsWhereas round 3 was the first round with enough participants to have any kind of interesting effects, round 4 felt like a true "coming-out party" for the cause of decentralized public goods funding. The round attracted a large amount of attention from the community, and even from outside actors such as the Bitcoin community. It is part of a broader trend in the last few months where public goods funding has become a dominant part of the crypto community discourse. Along with this, we have also seen much more discussion of strategies about long-term sources of funding for quadratic matching pools of larger sizes.Discussions about funding will be important going forward: donations from large Ethereum organizations are enough to sustain quadratic matching at its current scale, but not enough to allow it to grow much further, to the point where we can have hundreds of quadratic freelancers instead of about five. At those scales, sources of funding for Ethereum public goods must rely on network effect lockin to some extent, or else they will have little more staying power than individual donations, but there are strong reasons not to embed these funding sources too deeply into Ethereum (eg. into the protocol itself, a la the recent BCH proposal), to avoid risking the protocol's neutrality.Approaches based on capturing transaction fees at layer 2 are surprisingly viable: currently, there are about $50,000-100,000 per day (~$18-35m per year) of transaction fees happening on Ethereum, roughly equal to the entire budget of the Ethereum Foundation. And there is evidence that miner-extractable value is even higher. There are all discussions that we need to have, and challenges that we need to address, if we want the Ethereum community to be a leader in implementing decentralized, credibly neutral and market-based solutions to public goods funding challenges.
Review of Gitcoin Quadratic Funding Round 4 Review of Gitcoin Quadratic Funding Round 42020 Jan 28 See all posts Review of Gitcoin Quadratic Funding Round 4 Round 4 of Gitcoin Grants quadratic funding has just completed, and here are the results: The main distinction between round 3 and round 4 was that while round 3 had only one category, with mostly tech projects and a few outliers such as EthHub, in round 4 there were two separate categories, one with a $125,000 matching pool for tech projects, and the other with a $75,000 matching pool for "media" projects. Media could include documentation, translation, community activities, news reporting, theoretically pretty much anything in that category. And while the tech section went about largely without incident, in the new media section the results proved to be much more interesting than I could have possibly imagined, shedding a new light on deep questions in institutional design and political science.Tech: quadratic funding worked great as usualIn the tech section, the main changes that we see compared to round 3 are (i) the rise of Tornado Cash and (ii) the decline in importance of eth2 clients and the rise of "utility applications" of various forms. Tornado Cash is a trustless smart contract-based Ethereum mixer. It became popular quickly in recent months, as the Ethereum community was swept by worries about the blockchain's current low levels of privacy and wanted solutions. Tornado Cash amassed an incredible $31,200. If they continue receiving such an amount every two months then this would allow them to pay two people $7,800 per month each - meaning that the hoped-for milestone of seeing the first "quadratic freelancer" may have already been reached! The other major winners included tools like Dappnode, a software package to help people run nodes, Sablier, a payment streaming service, and DefiZap, which makes DeFi services easy to use. The Gitcoin Sustainability Fund got over $13,000, conclusively resolving my complaint from last round that they were under-supported. All in all, valuable grants for valuable projects that provide services that the community genuinely needs.We can see one major shift this round compared to the previous rounds. Whereas in previous rounds, the grants went largely to projects like eth2 clients that were already well-supported, this time the largest grants shifted toward having a different focus from the grants given by the Ethereum Foundation. The EF has not given grants to tornado.cash, and generally limits its grants to application-specific tools, Uniswap being a notable exception. The Gitcoin Grants quadratic fund, on the other hand, is supporting DeFiZap, Sablier, and many other tools that are valuable to the community. This is arguably a positive development, as it allows Gitcoin Grants and the Ethereum Foundation to complement each other rather than focusing on the same things.The one proposed change to the quadratic funding implementation for tech that I would favor is a user interface change, that makes it easier for users to commit funds for multiple rounds. This would increase the stability of contributions, thereby increasing the stability of projects' income - very important if we want "quadratic freelancer" to actually be a viable job category!Media: The First Quadratic Twitter FreelancerNow, we get to the new media section. In the first few days of the round, the leading recipient of the grants was "@antiprosynth Twitter account activity": an Ethereum community member who is very active on twitter promoting Ethereum and refuting misinformation from Bitcoin maximalists, asking for help from the Gitcoin QF crowd to.... fund his tweeting activities. At its peak, the projected matching going to @antiprosynth exceeded $20,000. This naturally proved to be controversial, with many criticizing this move and questioning whether or not a Twitter account is a legitimate public good: On the surface, it does indeed seem like someone getting paid $20,000 for operating a Twitter account is ridiculous. But it's worth digging in and questioning exactly what, if anything, is actually wrong with this outcome. After all, maybe this is what effective marketing in 2020 actually looks like, and it's our expectations that need to adapt.There are two main objections that I heard, and both lead to interesting criticisms of quadratic funding in its current implementation. First, there was criticism of overpayment. Twittering is a fairly "trivial" activity; it does not require that much work, lots of people do it for free, and it doesn't provide nearly as much long-term value as something more substantive like EthHub or the Zero Knowledge Podcast. Hence, it feels wrong to pay a full-time salary for it. Examples of @antiprosynth's recent tweetsIf we accept the metaphor of quadratic funding as being like a market for public goods, then one could simply extend the metaphor, and reply to the concern with the usual free-market argument. People voluntarily paid their own money to support @antiprosynth's twitter activity, and that itself signals that it's valuable. Why should we trust you with your mere words and protestations over a costly signal of real money on the table from dozens of people?The most plausible answer is actually quite similar to one that you often hear in discussions about financial markets: markets can give skewed results when you can express an opinion in favor of something but cannot express an opinion against it. When short selling is not possible, financial markets are often much more inefficient, because instead of reflecting the average opinion on an asset's true value, a market may instead reflect the inflated expectations of an asset's few rabid supporters. In this version of quadratic funding, there too is an asymmetry, as you can donate in support of a project but you cannot donate to oppose it. Might this be the root of the problem?One can go further and ask, why might overpayment happen to this particular project, and not others? I have heard a common answer: twitter accounts already have a high exposure. A client development team like Nethermind does not gain much publicity through their work directly, so they need to separately market themselves, whereas a twitter account's "work" is self-marketing by its very nature. Furthermore, the most prominent twitterers get quadratically more matching out of their exposure, amplifying their outsized advantage further - a problem I alluded to in my review of round 3.Interestingly, in the case of vanilla quadratic voting there was an argument made by Glen Weyl for why economies-of-scale effects of traditional voting, such as Duverger's law, don't apply to quadratic voting: a project becoming more prominent increases the incentive to give it both positive and negative votes, so on net the effects cancel out. But notice once again, that this argument relies on negative votes being a possibility.Good for the tribe, but is it good for the world?The particular story of @antiprosynth had what is in my opinion a happy ending: over the next ten days, more contributions came in to other candidates, and @antiprosynth's match reduced to $11,316, still a respectably high amount but on par with EthHub and below Week in Ethereum. However, even a quadratic matching grant of this size still raises to the next criticism: is twittering a public good or public bad anyway?Traditionally, public goods of the type that Gitcoin Grants quadratic funding is trying to support were selected and funded by governments. The motivation of @antiprosynth's tweets is "aggregating Ethereum-related news, fighting information asymmetry and fine-tuning/signaling a consistent narrative for Ethereum (and ETH)": essentially, fighting the good fight against anti-Ethereum misinformation by bitcoin maximalists. And, lo and behold, governments too have a rich history of sponsoring social media participants to argue on their behalf. And it seems likely that most of these governments see themselves as "fighting the good fight against anti-[X] misinformation by [Y] ", just as the Ethereum community feels a need to fight the good fight against maximalist trolls. From the inside view of each individual country (and in our case the Ethereum community) organized social media participation seems to be a clear public good (ignoring the possibility of blowback effects, which are real and important). But from the outside view of the entire world, it can be viewed as a zero-sum game. This is actually a common pattern to see in politics, and indeed there are many instances of larger-scale coordination that are precisely intended to undermine smaller-scale coordination that is seen as "good for the tribe but bad for the world": antitrust law, free trade agreements, state-level pre-emption of local zoning codes, anti-militarization agreements... the list goes on. A broad environment where public subsidies are generally viewed suspiciously also does quite a good job of limiting many kinds of malign local coordination. But as public goods become more important, and we discover better and better ways for communities to coordinate on producing them, that strategy's efficacy becomes more limited, and properly grappling with these discrepancies between what is good for the tribe and what is good for the world becomes more important.That said, internet marketing and debate is not a zero-sum game, and there are plenty of ways to engage in internet marketing and debate that are good for the world. Internet debate in general serves to help the public learn what things are true, what things are not true, what causes to support, and what causes to oppose. Some tactics are clearly not truth-favoring, but other tactics are quite truth-favoring. Some tactics are clearly offensive, but others are defensive. And in the ethereum community, there is widespread sentiment that there is not enough resources going into marketing of some kind, and I personally agree with this sentiment.What kind of marketing is positive-sum (good for tribe and good for world) and what kind of marketing is zero-sum (good for tribe but bad for world) is another question, and one that's worth the community debating. I naturally hope that the Ethereum community continues to value maintaining a moral high ground. Regarding the case of @antiprosynth himself, I cannot find any tactics that I would classify as bad-for-world, especially when compared to outright misinformation ("it's impossible to run a full node") that we often see used against Ethereum - but I am pro-ethereum and hence biased, hence the need to be careful.Universal mechanisms, particular goalsThe story has another plot twist, which reveals yet another feature (or bug?) or quadratic funding. Quadratic funding was originally described as "Formal Rules for a Society Neutral among Communities", the intention being to use it at a very large, potentially even global, scale. Anyone can participate as a project or as a participant, and projects that support public goods that are good for any "public" would be supported. In the case of Gitcoin Grants, however, the matching funds are coming from Ethereum organizations, and so there is an expectation that the system is there to support Ethereum projects. But there is nothing in the rules of quadratic funding that privileges Ethereum projects and prevents, say, Ethereum Classic projects from seeking funding using the same platform! And, of course, this is exactly what happened: So now the result is, $24 of funding from Ethereum organizations will be going toward supporting an Ethereum Classic promoter's twitter activity. To give people outside of the crypto space a feeling for what this is like, imagine the USA holding a quadratic funding raise, using government funding to match donations, and the result is that some of the funding goes to someone explicitly planning to use the money to talk on Twitter about how great Russia is (or vice versa). The matching funds are coming from Ethereum sources, and there's an implied expectation that the funds should support Ethereum, but nothing actually prevents, or even discourages, non-Ethereum projects from organizing to get a share of the matched funds on the platform!SolutionsThere are two solutions to these problems. One is to modify the quadratic funding mechanism to support negative votes in addition to positive votes. The mathematical theory behind quadratic voting already implies that it is the "right thing" to do to allow such a possibility (every positive number has a negative square root as well as a positive square root). On the other hand, there are social concerns that allowing for negative voting would cause more animosity and lead to other kinds of harms. After all, mob mentality is at its worst when it is against something rather than for something. Hence, it's my view that it's not certain that allowing negative contributions will work out well, but there is enough evidence that it might that it is definitely worth trying out in a future round.The second solution is to use two separate mechanisms for identifying relative goodness of good projects and for screening out bad projects. For example, one could use a challenge mechanism followed by a majority ETH coin vote, or even at first just a centralized appointed board, to screen out bad projects, and then use quadratic funding as before to choose between good projects. This is less mathematically elegant, but it would solve the problem, and it would at the same time provide an opportunity to mix in a separate mechanism to ensure that chosen projects benefit Ethereum specifically.But even if we adopt the first solution, defining boundaries for the quadratic funding itself may also be a good idea. There is intellectual precedent for this. In Elinor Ostrom's eight principles for governing the commons, defining clear boundaries about who has the right to access the commons is the first one. Without clear boundaries, Ostrom writes, "local appropriators face the risk that any benefits they produce by their efforts will be reaped by others who have not contributed to those efforts." In the case of Gitcoin Grants quadratic funding, one possibility would be to set the maximum matching coefficient for any pair of users to be proportional to the geometric average of their ETH holdings, using that as a proxy for measuring membership in the Ethereum community (note that this avoids being plutocratic because 1000 users with 1 ETH each would have a maximum matching of \(\approx k * 500,000\) ETH, whereas 2 users with 500 ETH each would only have a maximum matching of \(k * 1,000\) ETH).CollusionAnother issue that came to the forefront this round was the issue of collusion. The math behind quadratic funding, which compensates for tragedies of the commons by magnifying individual contributions based on the total number and size of other contributions to the same project, only works if there is an actual tragedy of the commons limiting natural donations to the project. If there is a "quid pro quo", where people get something individually in exchange for their contributions, the mechanism can easily over-compensate. The long-run solution to this is something like MACI, a cryptographic system that ensures that contributors have no way to prove their contributions to third parties, so any such collusion would have to be done by honor system. In the short run, however, the rules and enforcement has not yet been set, and this has led to vigorous debate about what kinds of quid pro quo are legitimate: [Update 2020.01.29: the above was ultimately a result of a miscommunication from Gitcoin; a member of the Gitcoin team had okayed Richard Burton's proposal to give rewards to donors without realizing the implications. So Richard himself is blameless here; though the broader point that we underestimated the need for explicit guidance about what kinds of quid pro quos are acceptable is very much real.]Currently, the position is that quid pro quos are disallowed, though there is a more nuanced feeling that informal social quid pro quos ("thank yous" of different forms) are okay, whereas formal and especially monetary or product rewards are a no-no. This seems like a reasonable approach, though it does put Gitcoin further into the uncomfortable position of being a central arbiter, compromising credible neutrality somewhat. One positive byproduct of this whole discussion is that it has led to much more awareness in the Ethereum community of what actually is a public good (as opposed to a "private good" or a "club good"), and more generally brought public goods much further into the public discourse.ConclusionsWhereas round 3 was the first round with enough participants to have any kind of interesting effects, round 4 felt like a true "coming-out party" for the cause of decentralized public goods funding. The round attracted a large amount of attention from the community, and even from outside actors such as the Bitcoin community. It is part of a broader trend in the last few months where public goods funding has become a dominant part of the crypto community discourse. Along with this, we have also seen much more discussion of strategies about long-term sources of funding for quadratic matching pools of larger sizes.Discussions about funding will be important going forward: donations from large Ethereum organizations are enough to sustain quadratic matching at its current scale, but not enough to allow it to grow much further, to the point where we can have hundreds of quadratic freelancers instead of about five. At those scales, sources of funding for Ethereum public goods must rely on network effect lockin to some extent, or else they will have little more staying power than individual donations, but there are strong reasons not to embed these funding sources too deeply into Ethereum (eg. into the protocol itself, a la the recent BCH proposal), to avoid risking the protocol's neutrality.Approaches based on capturing transaction fees at layer 2 are surprisingly viable: currently, there are about $50,000-100,000 per day (~$18-35m per year) of transaction fees happening on Ethereum, roughly equal to the entire budget of the Ethereum Foundation. And there is evidence that miner-extractable value is even higher. There are all discussions that we need to have, and challenges that we need to address, if we want the Ethereum community to be a leader in implementing decentralized, credibly neutral and market-based solutions to public goods funding challenges. -
 A Quick Garbled Circuits Primer A Quick Garbled Circuits Primer2020 Mar 21 See all posts A Quick Garbled Circuits Primer Special thanks to Dankrad Feist for reviewGarbled circuits are a quite old, and surprisingly simple, cryptographic primitive; they are quite possibly the simplest form of general-purpose "multi-party computation" (MPC) to wrap your head around.Here is the usual setup for the scheme:Suppose that there are two parties, Alice and Bob, who want to compute some function f(alice_inputs, bob_inputs), which takes inputs from both parties. Alice and Bob want to both learn the result of computing f, but Alice does not want Bob to learn her inputs, and Bob does not want Alice to learn his inputs. Ideally, they would both learn nothing except for just the output of f. Alice performs a special procedure ("garbling") to encrypt a circuit (meaning, a set of AND, OR... gates) which evaluates the function f. She passes along inputs, also encrypted in a way that's compatible with the encrypted circuit, to Bob. Bob uses a technique called "1-of-2 oblivious transfer" to learn the encrypted form of his own inputs, without letting Alice know which inputs he obtained. Bob runs the encrypted circuit on the encrypted data and gets the answer, and passes it along to Alice. Extra cryptographic wrappings can be used to protect the scheme against Alice and Bob sending wrong info and giving each other an incorrect answer; we won't go into those here for simplicity, though it suffices to say "wrap a ZK-SNARK around everything" is one (quite heavy duty and suboptimal!) solution that works fine.So how does the basic scheme work? Let's start with a circuit: This is one of the simplest examples of a not-completely-trivial circuit that actually does something: it's a two-bit adder. It takes as input two numbers in binary, each with two bits, and outputs the three-bit binary number that is the sum.Now, let's encrypt the circuit. First, for every input, we randomly generate two "labels" (think: 256-bit numbers): one to represent that input being 0 and the other to represent that input being 1. Then we also do the same for every intermediate wire, not including the output wires. Note that this data is not part of the "garbling" that Alice sends to Bob; so far this is just setup. Now, for every gate in the circuit, we do the following. For every combination of inputs, we include in the "garbling" that Alice provides to Bob the label of the output (or if the label of the output is a "final" output, the output directly) encrypted with a key generated by hashing the input labels that lead to that output together. For simplicity, our encryption algorithm can just be enc(out, in1, in2) = out + hash(k, in1, in2) where k is the index of the gate (is it the first gate in the circuit, the second, the third?). If you know the labels of both inputs, and you have the garbling, then you can learn the label of the corresponding output, because you can just compute the corresponding hash and subtract it out.Here's the garbling of the first XOR gate:Inputs Output Encoding of output 00 0 0 + hash(1, 6816, 6529) 01 1 1 + hash(1, 6816, 4872) 10 1 1 + hash(1, 8677, 6529) 11 0 0 + hash(1, 8677, 4872) Notice that we are including the (encrypted forms of) 0 and 1 directly, because this XOR gate's outputs are directly final outputs of the program. Now, let's look at the leftmost AND gate:Inputs Output Encoding of output 00 0 5990 + hash(2, 6816, 6529) 01 0 5990 + hash(2, 6816, 4872) 10 0 5990 + hash(2, 8677, 6529) 11 1 1921 + hash(2, 8677, 4872) Here, the gate's outputs are just used as inputs to other gates, so we use labels instead of bits to hide these intermediate bits from the evaluator.The "garbling" that Alice would provide to Bob is just everything in the third column for each gate, with the rows of each gate re-ordered (to avoid revealing whether a given row corresponds to a 0 or a 1 in any wire). To help Bob learn which value to decrypt for each gate, we'll use a particular order: for each gate, the first row becomes the row where both input labels are even, in the second row the second label is odd, in the third row the first label is odd, and in the fourth row both labels are odd (we deliberately chose labels earlier so that each gate would have an even label for one output and an odd label for the other). We garble every other gate in the circuit in the same way.All in all, Alice sends to Bob four ~256 bit numbers for each gate in the circuit. It turns out that four is far from optimal; see here for some optimizations on how to reduce this to three or even two numbers for an AND gate and zero (!!) for an XOR gate. Note that these optimizations do rely on some changes, eg. using XOR instead of addition and subtraction, though this should be done anyway for security.When Bob receives the circuit, he asks Alice for the labels corresponding to her input, and he uses a protocol called "1-of-2 oblivious transfer" to ask Alice for the labels corresponding to his own input without revealing to Alice what his input is. He then goes through the gates in the circuit one by one, uncovering the output wires of each intermediate gate.Suppose Alice's input is the two left wires and she gives (0, 1), and Bob's input is the two right wires and he gives (1, 1). Here's the circuit with labels again: At the start, Bob knows the labels 6816, 3621, 4872, 5851 Bob evaluates the first gate. He knows 6816 and 4872, so he can extract the output value corresponding to (1, 6816, 4872) (see the table above) and extracts the first output bit, 1 Bob evaluates the second gate. He knows 6816 and 4872, so he can extract the output value corresponding to (2, 6816, 4872) (see the table above) and extracts the label 5990 Bob evaluates the third gate (XOR). He knows 3621 and 5851, and learns 7504 Bob evaluates the fourth gate (OR). He knows 3621 and 5851, and learns 6638 Bob evaluates the fifth gate (AND). He knows 3621 and 5851, and learns 7684 Bob evaluates the sixth gate (XOR). He knows 5990 and 7504, and learns the second output bit, 0 Bob evaluates the seventh gate (AND). He knows 5990 and 6638, and learns 8674 Bob evaluates the eighth gate (OR). He knows 8674 and 7684, and learns the third output bit, 1 And so Bob learns the output: 101. And in binary 10 + 11 actually equals 101 (the input and output bits are both given in smallest-to-greatest order in the circuit, which is why Alice's input 10 is represented as (0, 1) in the circuit), so it worked!Note that addition is a fairly pointless use of garbled circuits, because Bob knowing 101 can just subtract out his own input and get 101 - 11 = 10 (Alice's input), breaking privacy. However, in general garbled circuits can be used for computations that are not reversible, and so don't break privacy in this way (eg. one might imagine a computation where Alice's input and Bob's input are their answers to a personality quiz, and the output is a single bit that determines whether or not the algorithm thinks they are compatible; that one bit of information won't let Alice or Bob know anything about each other's individual quiz answers).1 of 2 Oblivious TransferNow let us talk more about 1-of-2 oblivious transfer, this technique that Bob used to obtain the labels from Alice corresponding to his own input. The problem is this. Focusing on Bob's first input bit (the algorithm for the second input bit is the same), Alice has a label corresponding to 0 (6529), and a label corresponding to 1 (4872). Bob has his desired input bit: 1. Bob wants to learn the correct label (4872) without letting Alice know that his input bit is 1. The trivial solution (Alice just sends Bob both 6529 and 4872) doesn't work because Alice only wants to give up one of the two input labels; if Bob receives both input labels this could leak data that Alice doesn't want to give up.Here is a fairly simple protocol using elliptic curves:Alice generates a random elliptic curve point, H. Bob generates two points, P1 and P2, with the requirement that P1 + P2 sums to H. Bob chooses either P1 or P2 to be G * k (ie. a point that he knows the corresponding private key for). Note that the requirement that P1 + P2 = H ensures that Bob has no way to generate P1 and P2 such that he knows the corresponding private key for. This is because if P1 = G * k1 and P2 = G * k2 where Bob knows both k1 and k2, then H = G * (k1 + k2), so that would imply Bob can extract the discrete logarithm (or "corresponding private key") for H, which would imply all of elliptic curve cryptography is broken. Alice confirms P1 + P2 = H, and encrypts v1 under P1 and v2 under P2 using some standard public key encryption scheme (eg. El-Gamal). Bob is only able to decrypt one of the two values, because he knows the private key corresponding to at most one of (P1, P2), but Alice does not know which one. This solves the problem; Bob learns one of the two wire labels (either 6529 or 4872), depending on what his input bit is, and Alice does not know which label Bob learned.ApplicationsGarbled circuits are potentially useful for many more things than just 2-of-2 computation. For example, you can use them to make multi-party computations of arbitrary complexity with an arbitrary number of participants providing inputs, that can run in a constant number of rounds of interaction. Generating a garbled circuit is completely parallelizable; you don't need to finish garbling one gate before you can start garbling gates that depend on it. Hence, you can simply have a large multi-party computation with many participants compute a garbling of all gates of a circuit and publish the labels corresponding to their inputs. The labels themselves are random and so reveal nothing about the inputs, but anyone can then execute the published garbled circuit and learn the output "in the clear". See here for a recent example of an MPC protocol that uses garbling as an ingredient.Multi-party computation is not the only context where this technique of splitting up a computation into a parallelizable part that operates on secret data followed by a sequential part that can be run in the clear is useful, and garbled circuits are not the only technique for accomplishing this. In general, the literature on randomized encodings includes many more sophisticated techniques. This branch of math is also useful in technologies such as functional encryption and obfuscation.
A Quick Garbled Circuits Primer A Quick Garbled Circuits Primer2020 Mar 21 See all posts A Quick Garbled Circuits Primer Special thanks to Dankrad Feist for reviewGarbled circuits are a quite old, and surprisingly simple, cryptographic primitive; they are quite possibly the simplest form of general-purpose "multi-party computation" (MPC) to wrap your head around.Here is the usual setup for the scheme:Suppose that there are two parties, Alice and Bob, who want to compute some function f(alice_inputs, bob_inputs), which takes inputs from both parties. Alice and Bob want to both learn the result of computing f, but Alice does not want Bob to learn her inputs, and Bob does not want Alice to learn his inputs. Ideally, they would both learn nothing except for just the output of f. Alice performs a special procedure ("garbling") to encrypt a circuit (meaning, a set of AND, OR... gates) which evaluates the function f. She passes along inputs, also encrypted in a way that's compatible with the encrypted circuit, to Bob. Bob uses a technique called "1-of-2 oblivious transfer" to learn the encrypted form of his own inputs, without letting Alice know which inputs he obtained. Bob runs the encrypted circuit on the encrypted data and gets the answer, and passes it along to Alice. Extra cryptographic wrappings can be used to protect the scheme against Alice and Bob sending wrong info and giving each other an incorrect answer; we won't go into those here for simplicity, though it suffices to say "wrap a ZK-SNARK around everything" is one (quite heavy duty and suboptimal!) solution that works fine.So how does the basic scheme work? Let's start with a circuit: This is one of the simplest examples of a not-completely-trivial circuit that actually does something: it's a two-bit adder. It takes as input two numbers in binary, each with two bits, and outputs the three-bit binary number that is the sum.Now, let's encrypt the circuit. First, for every input, we randomly generate two "labels" (think: 256-bit numbers): one to represent that input being 0 and the other to represent that input being 1. Then we also do the same for every intermediate wire, not including the output wires. Note that this data is not part of the "garbling" that Alice sends to Bob; so far this is just setup. Now, for every gate in the circuit, we do the following. For every combination of inputs, we include in the "garbling" that Alice provides to Bob the label of the output (or if the label of the output is a "final" output, the output directly) encrypted with a key generated by hashing the input labels that lead to that output together. For simplicity, our encryption algorithm can just be enc(out, in1, in2) = out + hash(k, in1, in2) where k is the index of the gate (is it the first gate in the circuit, the second, the third?). If you know the labels of both inputs, and you have the garbling, then you can learn the label of the corresponding output, because you can just compute the corresponding hash and subtract it out.Here's the garbling of the first XOR gate:Inputs Output Encoding of output 00 0 0 + hash(1, 6816, 6529) 01 1 1 + hash(1, 6816, 4872) 10 1 1 + hash(1, 8677, 6529) 11 0 0 + hash(1, 8677, 4872) Notice that we are including the (encrypted forms of) 0 and 1 directly, because this XOR gate's outputs are directly final outputs of the program. Now, let's look at the leftmost AND gate:Inputs Output Encoding of output 00 0 5990 + hash(2, 6816, 6529) 01 0 5990 + hash(2, 6816, 4872) 10 0 5990 + hash(2, 8677, 6529) 11 1 1921 + hash(2, 8677, 4872) Here, the gate's outputs are just used as inputs to other gates, so we use labels instead of bits to hide these intermediate bits from the evaluator.The "garbling" that Alice would provide to Bob is just everything in the third column for each gate, with the rows of each gate re-ordered (to avoid revealing whether a given row corresponds to a 0 or a 1 in any wire). To help Bob learn which value to decrypt for each gate, we'll use a particular order: for each gate, the first row becomes the row where both input labels are even, in the second row the second label is odd, in the third row the first label is odd, and in the fourth row both labels are odd (we deliberately chose labels earlier so that each gate would have an even label for one output and an odd label for the other). We garble every other gate in the circuit in the same way.All in all, Alice sends to Bob four ~256 bit numbers for each gate in the circuit. It turns out that four is far from optimal; see here for some optimizations on how to reduce this to three or even two numbers for an AND gate and zero (!!) for an XOR gate. Note that these optimizations do rely on some changes, eg. using XOR instead of addition and subtraction, though this should be done anyway for security.When Bob receives the circuit, he asks Alice for the labels corresponding to her input, and he uses a protocol called "1-of-2 oblivious transfer" to ask Alice for the labels corresponding to his own input without revealing to Alice what his input is. He then goes through the gates in the circuit one by one, uncovering the output wires of each intermediate gate.Suppose Alice's input is the two left wires and she gives (0, 1), and Bob's input is the two right wires and he gives (1, 1). Here's the circuit with labels again: At the start, Bob knows the labels 6816, 3621, 4872, 5851 Bob evaluates the first gate. He knows 6816 and 4872, so he can extract the output value corresponding to (1, 6816, 4872) (see the table above) and extracts the first output bit, 1 Bob evaluates the second gate. He knows 6816 and 4872, so he can extract the output value corresponding to (2, 6816, 4872) (see the table above) and extracts the label 5990 Bob evaluates the third gate (XOR). He knows 3621 and 5851, and learns 7504 Bob evaluates the fourth gate (OR). He knows 3621 and 5851, and learns 6638 Bob evaluates the fifth gate (AND). He knows 3621 and 5851, and learns 7684 Bob evaluates the sixth gate (XOR). He knows 5990 and 7504, and learns the second output bit, 0 Bob evaluates the seventh gate (AND). He knows 5990 and 6638, and learns 8674 Bob evaluates the eighth gate (OR). He knows 8674 and 7684, and learns the third output bit, 1 And so Bob learns the output: 101. And in binary 10 + 11 actually equals 101 (the input and output bits are both given in smallest-to-greatest order in the circuit, which is why Alice's input 10 is represented as (0, 1) in the circuit), so it worked!Note that addition is a fairly pointless use of garbled circuits, because Bob knowing 101 can just subtract out his own input and get 101 - 11 = 10 (Alice's input), breaking privacy. However, in general garbled circuits can be used for computations that are not reversible, and so don't break privacy in this way (eg. one might imagine a computation where Alice's input and Bob's input are their answers to a personality quiz, and the output is a single bit that determines whether or not the algorithm thinks they are compatible; that one bit of information won't let Alice or Bob know anything about each other's individual quiz answers).1 of 2 Oblivious TransferNow let us talk more about 1-of-2 oblivious transfer, this technique that Bob used to obtain the labels from Alice corresponding to his own input. The problem is this. Focusing on Bob's first input bit (the algorithm for the second input bit is the same), Alice has a label corresponding to 0 (6529), and a label corresponding to 1 (4872). Bob has his desired input bit: 1. Bob wants to learn the correct label (4872) without letting Alice know that his input bit is 1. The trivial solution (Alice just sends Bob both 6529 and 4872) doesn't work because Alice only wants to give up one of the two input labels; if Bob receives both input labels this could leak data that Alice doesn't want to give up.Here is a fairly simple protocol using elliptic curves:Alice generates a random elliptic curve point, H. Bob generates two points, P1 and P2, with the requirement that P1 + P2 sums to H. Bob chooses either P1 or P2 to be G * k (ie. a point that he knows the corresponding private key for). Note that the requirement that P1 + P2 = H ensures that Bob has no way to generate P1 and P2 such that he knows the corresponding private key for. This is because if P1 = G * k1 and P2 = G * k2 where Bob knows both k1 and k2, then H = G * (k1 + k2), so that would imply Bob can extract the discrete logarithm (or "corresponding private key") for H, which would imply all of elliptic curve cryptography is broken. Alice confirms P1 + P2 = H, and encrypts v1 under P1 and v2 under P2 using some standard public key encryption scheme (eg. El-Gamal). Bob is only able to decrypt one of the two values, because he knows the private key corresponding to at most one of (P1, P2), but Alice does not know which one. This solves the problem; Bob learns one of the two wire labels (either 6529 or 4872), depending on what his input bit is, and Alice does not know which label Bob learned.ApplicationsGarbled circuits are potentially useful for many more things than just 2-of-2 computation. For example, you can use them to make multi-party computations of arbitrary complexity with an arbitrary number of participants providing inputs, that can run in a constant number of rounds of interaction. Generating a garbled circuit is completely parallelizable; you don't need to finish garbling one gate before you can start garbling gates that depend on it. Hence, you can simply have a large multi-party computation with many participants compute a garbling of all gates of a circuit and publish the labels corresponding to their inputs. The labels themselves are random and so reveal nothing about the inputs, but anyone can then execute the published garbled circuit and learn the output "in the clear". See here for a recent example of an MPC protocol that uses garbling as an ingredient.Multi-party computation is not the only context where this technique of splitting up a computation into a parallelizable part that operates on secret data followed by a sequential part that can be run in the clear is useful, and garbled circuits are not the only technique for accomplishing this. In general, the literature on randomized encodings includes many more sophisticated techniques. This branch of math is also useful in technologies such as functional encryption and obfuscation. -
 Quadratic Payments: A Primer Quadratic Payments: A Primer2019 Dec 07 See all posts Quadratic Payments: A Primer Special thanks to Karl Floersch and Jinglan Wang for feedbackIf you follow applied mechanism design or decentralized governance at all, you may have recently heard one of a few buzzwords: quadratic voting, quadratic funding and quadratic attention purchase. These ideas have been gaining popularity rapidly over the last few years, and small-scale tests have already been deployed: the Taiwanese presidential hackathon used quadratic voting to vote on winning projects, Gitcoin Grants used quadratic funding to fund public goods in the Ethereum ecosystem, and the Colorado Democratic party also experimented with quadratic voting to determine their party platform.To the proponents of these voting schemes, this is not just another slight improvement to what exists. Rather, it's an initial foray into a fundamentally new class of social technology which, has the potential to overturn how we make many public decisions, large and small. The ultimate effect of these schemes rolled out in their full form could be as deeply transformative as the industrial-era advent of mostly-free markets and constitutional democracy. But now, you may be thinking: "These are large promises. What do these new governance technologies have that justifies such claims?"Private goods, private markets...To understand what is going on, let us first consider an existing social technology: money, and property rights - the invisible social technology that generally hides behind money. Money and private property are extremely powerful social technologies, for all the reasons classical economists have been stating for over a hundred years. If Bob is producing apples, and Alice wants to buy apples, we can economically model the interaction between the two, and the results seem to make sense: Alice keeps buying apples until the marginal value of the next apple to her is less than the cost of producing it, which is pretty much exactly the optimal thing that could happen. This is all formalized in results such as the "fundamental theorems of welfare economics". Now, those of you who have learned some economics may be screaming, but what about imperfect competition? Asymmetric information? Economic inequality? Public goods? Externalities? Many activities in the real world, including those that are key to the progress of human civilization, benefit (or harm) many people in complicated ways. These activities and the consequences that arise from them often cannot be neatly decomposed into sequences of distinct trades between two parties.But since when do we expect a single package of technologies to solve every problem anyway? "What about oceans?" isn't an argument against cars, it's an argument against car maximalism, the position that we need cars and nothing else. Much like how private property and markets deal with private goods, can we try to use economic means to deduce what kind of social technologies would work well for encouraging production of the public goods that we need?... Public goods, public marketsPrivate goods (eg. apples) and public goods (eg. public parks, air quality, scientific research, this article...) are different in some key ways. When we are talking about private goods, production for multiple people (eg. the same farmer makes apples for both Alice and Bob) can be decomposed into (i) the farmer making some apples for Alice, and (ii) the farmer making some other apples for Bob. If Alice wants apples but Bob does not, then the farmer makes Alice's apples, collects payment from Alice, and leaves Bob alone. Even complex collaborations (the "I, Pencil" essay popular in libertarian circles comes to mind) can be decomposed into a series of such interactions. When we are talking about public goods, however, this kind of decomposition is not possible. When I write this blog article, it can be read by both Alice and Bob (and everyone else). I could put it behind a paywall, but if it's popular enough it will inevitably get mirrored on third-party sites, and paywalls are in any case annoying and not very effective. Furthermore, making an article available to ten people is not ten times cheaper than making the article available to a hundred people; rather, the cost is exactly the same. So I either produce the article for everyone, or I do not produce it for anyone at all.So here comes the challenge: how do we aggregate together people's preferences? Some private and public goods are worth producing, others are not. In the case of private goods, the question is easy, because we can just decompose it into a series of decisions for each individual. Whatever amount each person is willing to pay for, that much gets produced for them; the economics is not especially complex. In the case of public goods, however, you cannot "decompose", and so we need to add up people's preferences in a different way.First of all, let's see what happens if we just put up a plain old regular market: I offer to write an article as long as at least $1000 of money gets donated to me (fun fact: I literally did this back in 2011). Every dollar donated increases the probability that the goal will be reached and the article will be published; let us call this "marginal probability" p. At a cost of $k, you can increase the probability that the article will be published by k * p (though eventually the gains will decrease as the probability approaches 100%). Let's say to you personally, the article being published is worth $V. Would you donate? Well, donating a dollar increases the probability it will be published by p, and so gives you an expected $p * V of value. If p * V > 1, you donate, and quite a lot, and if p * V < 1 you don't donate at all.Phrased less mathematically, either you value the article enough (and/or are rich enough) to pay, and if that's the case it's in your interest to keep paying (and influencing) quite a lot, or you don't value the article enough and you contribute nothing. Hence, the only blog articles that get published would be articles where some single person is willing to basically pay for it themselves (in my experiment in 2011, this prediction was experimentally verified: in most rounds, over half of the total contribution came from a single donor). Note that this reasoning applies for any kind of mechanism that involves "buying influence" over matters of public concern. This includes paying for public goods, shareholder voting in corporations, public advertising, bribing politicians, and much more. The little guy has too little influence (not quite zero, because in the real world things like altruism exist) and the big guy has too much. If you had an intuition that markets work great for buying apples, but money is corrupting in "the public sphere", this is basically a simplified mathematical model that shows why.We can also consider a different mechanism: one-person-one-vote. Let's say you can either vote that I deserve a reward for writing this article, or you can vote that I don't, and my reward is proportional to the number of votes in my favor. We can interpret this as follows: your first "contribution" costs only a small amount of effort, so you'll support an article if you care about it enough, but after that point there is no more room to contribute further; your second contribution "costs" infinity. Now, you might notice that neither of the graphs above look quite right. The first graph over-privileges people who care a lot (or are wealthy), the second graph over-privileges people who care only a little, which is also a problem. The single sheep's desire to live is more important than the two wolves' desire to have a tasty dinner.But what do we actually want? Ultimately, we want a scheme where how much influence you "buy" is proportional to how much you care. In the mathematical lingo above, we want your k to be proportional to your V. But here's the problem: your V determines how much you're willing to pay for one unit of influence. If Alice were willing to pay $100 for the article if she had to fund it herself, then she would be willing to pay $1 for an increased 1% chance it will get written, and if Bob were only willing to pay $50 for the article then he would only be willing to pay $0.5 for the same "unit of influence".So how do we match these two up? The answer is clever: your n'th unit of influence costs you $n . That is, for example, you could buy your first vote for $0.01, but then your second would cost $0.02, your third $0.03, and so forth. Suppose you were Alice in the example above; in such a system she would keep buying units of influence until the cost of the next one got to $1, so she would buy 100 units. Bob would similarly buy until the cost got to $0.5, so he would buy 50 units. Alice's 2x higher valuation turned into 2x more units of influence purchased.Let's draw this as a graph: Now let's look at all three beside each other:One dollar one vote Quadratic voting One person one vote Notice that only quadratic voting has this nice property that the amount of influence you purchase is proportional to how much you care; the other two mechanisms either over-privilege concentrated interests or over-privilege diffuse interests.Now, you might ask, where does the quadratic come from? Well, the marginal cost of the n'th vote is $n (or $0.01 * n), but the total cost of n votes is \(\approx \frac\). You can view this geometrically as follows: The total cost is the area of a triangle, and you probably learned in math class that area is base * height / 2. And since here base and height are proportionate, that basically means that total cost is proportional to number of votes squared - hence, "quadratic". But honestly it's easier to think "your n'th unit of influence costs $n".Finally, you might notice that above I've been vague about what "one unit of influence" actually means. This is deliberate; it can mean different things in different contexts, and the different "flavors" of quadratic payments reflect these different perspectives.Quadratic VotingSee also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=2003531Let us begin by exploring the first "flavor" of quadratic payments: quadratic voting. Imagine that some organization is trying to choose between two choices for some decision that affects all of its members. For example, this could be a company or a nonprofit deciding which part of town to make a new office in, or a government deciding whether or not to implement some policy, or an internet forum deciding whether or not its rules should allow discussion of cryptocurrency prices. Within the context of the organization, the choice made is a public good (or public bad, depending on whom you talk to): everyone "consumes" the results of the same decision, they just have different opinions about how much they like the result.This seems like a perfect target for quadratic voting. The goal is that option A gets chosen if in total people like A more, and option B gets chosen if in total people like B more. With simple voting ("one person one vote"), the distinction between stronger vs weaker preferences gets ignored, so on issues where one side is of very high value to a few people and the other side is of low value to more people, simple voting is likely to give wrong answers. With a private-goods market mechanism where people can buy as many votes as they want at the same price per vote, the individual with the strongest preference (or the wealthiest) carries everything. Quadratic voting, where you can make n votes in either direction at a cost of n2, is right in the middle between these two extremes, and creates the perfect balance. Note that in the voting case, we're deciding two options, so different people will favor A over B or B over A; hence, unlike the graphs we saw earlier that start from zero, here voting and preference can both be positive or negative (which option is considered positive and which is negative doesn't matter; the math works out the same way)As shown above, because the n'th vote has a cost of n, the number of votes you make is proportional to how much you value one unit of influence over the decision (the value of the decision multiplied by the probability that one vote will tip the result), and hence proportional to how much you care about A being chosen over B or vice versa. Hence, we once again have this nice clean "preference adding" effect.We can extend quadratic voting in multiple ways. First, we can allow voting between more than two options. While traditional voting schemes inevitably fall prey to various kinds of "strategic voting" issues because of Arrow's theorem and Duverger's law, quadratic voting continues to be optimal in contexts with more than two choices.The intuitive argument for those interested: suppose there are established candidates A and B and new candidate C. Some people favor C > A > B but others C > B > A. in a regular vote, if both sides think C stands no chance, they decide may as well vote their preference between A and B, so C gets no votes, and C's failure becomes a self-fulfilling prophecy. In quadratic voting the former group would vote [A +10, B -10, C +1] and the latter [A -10, B +10, C +1], so the A and B votes cancel out and C's popularity shines through.Second, we can look not just at voting between discrete options, but also at voting on the setting of a thermostat: anyone can push the thermostat up or down by 0.01 degrees n times by paying a cost of n2. Plot twist: the side wanting it colder only wins when they convince the other side that "C" stands for "caliente". Quadratic fundingSee also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=3243656Quadratic voting is optimal when you need to make some fixed number of collective decisions. But one weakness of quadratic voting is that it doesn't come with a built-in mechanism for deciding what goes on the ballot in the first place. Proposing votes is potentially a source of considerable power if not handled with care: a malicious actor in control of it can repeatedly propose some decision that a majority weakly approves of and a minority strongly disapproves of, and keep proposing it until the minority runs out of voting tokens (if you do the math you'll see that the minority would burn through tokens much faster than the majority). Let's consider a flavor of quadratic payments that does not run into this issue, and makes the choice of decisions itself endogenous (ie. part of the mechanism itself). In this case, the mechanism is specialized for one particular use case: individual provision of public goods.Let us consider an example where someone is looking to produce a public good (eg. a developer writing an open source software program), and we want to figure out whether or not this program is worth funding. But instead of just thinking about one single public good, let's create a mechanism where anyone can raise funds for what they claim to be a public good project. Anyone can make a contribution to any project; a mechanism keeps track of these contributions and then at the end of some period of time the mechanism calculates a payment to each project. The way that this payment is calculated is as follows: for any given project, take the square root of each contributor's contribution, add these values together, and take the square of the result. Or in math speak:\[(\sum_^n \sqrt)^2\]If that sounds complicated, here it is graphically: In any case where there is more than one contributor, the computed payment is greater than the raw sum of contributions; the difference comes out of a central subsidy pool (eg. if ten people each donate $1, then the sum-of-square-roots is $10, and the square of that is $100, so the subsidy is $90). Note that if the subsidy pool is not big enough to make the full required payment to every project, we can just divide the subsidies proportionately by whatever constant makes the totals add up to the subsidy pool's budget; you can prove that this solves the tragedy-of-the-commons problem as well as you can with that subsidy budget.There are two ways to intuitively interpret this formula. First, one can look at it through the "fixing market failure" lens, a surgical fix to the tragedy of the commons problem. In any situation where Alice contributes to a project and Bob also contributes to that same project, Alice is making a contribution to something that is valuable not only to herself, but also to Bob. When deciding how much to contribute, Alice was only taking into account the benefit to herself, not Bob, whom she most likely does not even know. The quadratic funding mechanism adds a subsidy to compensate for this effect, determining how much Alice "would have" contributed if she also took into account the benefit her contribution brings to Bob. Furthermore, we can separately calculate the subsidy for each pair of people (nb. if there are N people there are N * (N-1) / 2 pairs), and add up all of these subsidies together, and give Bob the combined subsidy from all pairs. And it turns out that this gives exactly the quadratic funding formula.Second, one can look at the formula through a quadratic voting lens. We interpret the quadratic funding as being a special case of quadratic voting, where the contributors to a project are voting for that project and there is one imaginary participant voting against it: the subsidy pool. Every "project" is a motion to take money from the subsidy pool and give it to that project's creator. Everyone sending \(c_i\) of funds is making \(\sqrt\) votes, so there's a total of \(\sum_^n \sqrt\) votes in favor of the motion. To kill the motion, the subsidy pool would need to make more than \(\sum_^n \sqrt\) votes against it, which would cost it more than \((\sum_^n \sqrt)^2\). Hence, \((\sum_^n \sqrt)^2\) is the maximum transfer from the subsidy pool to the project that the subsidy pool would not vote to stop.Quadratic funding is starting to be explored as a mechanism for funding public goods already; Gitcoin grants for funding public goods in the Ethereum ecosystem is currently the biggest example, and the most recent round led to results that, in my own view, did a quite good job of making a fair allocation to support projects that the community deems valuable. Numbers in white are raw contribution totals; numbers in green are the extra subsidies. Quadratic attention paymentsSee also the original post: https://kortina.nyc/essays/speech-is-free-distribution-is-not-a-tax-on-the-purchase-of-human-attention-and-political-power/One of the defining features of modern capitalism that people love to hate is ads. Our cities have ads: Source: https://www.flickr.com/photos/argonavigo/36657795264 Our subway turnstiles have ads: Source: https://commons.wikimedia.org/wiki/File:NYC,_subway_ad_on_Prince_St.jpg Our politics are dominated by ads: Source: https://upload.wikimedia.org/wikipedia/commons/e/e3/Billboard_Challenging_the_validity_of_Barack_Obama%27s_Birth_Certificate.JPG And even the rivers and the skies have ads. Now, there are some places that seem to not have this problem: But really they just have a different kind of ads: Now, recently there are attempts to move beyond this in some cities. And on Twitter. But let's look at the problem systematically and try to see what's going wrong. The answer is actually surprisingly simple: public advertising is the evil twin of public goods production. In the case of public goods production, there is one actor that is taking on an expenditure to produce some product, and this product benefits a large number of people. Because these people cannot effectively coordinate to pay for the public goods by themselves, we get much less public goods than we need, and the ones we do get are those favored by wealthy actors or centralized authorities. Here, there is one actor that reaps a large benefit from forcing other people to look at some image, and this action harms a large number of people. Because these people cannot effectively coordinate to buy out the slots for the ads, we get ads we don't want to see, that are favored by... wealthy actors or centralized authorities.So how do we solve this dark mirror image of public goods production? With a bright mirror image of quadratic funding: quadratic fees! Imagine a billboard where anyone can pay $1 to put up an ad for one minute, but if they want to do this multiple times the prices go up: $2 for the second minute, $3 for the third minute, etc. Note that you can pay to extend the lifetime of someone else's ad on the billboard, and this also costs you only $1 for the first minute, even if other people already paid to extend the ad's lifetime many times. We can once again interpret this as being a special case of quadratic voting: it's basically the same as the "voting on a thermostat" example above, but where the thermostat in question is the number of seconds an ad stays up.This kind of payment model could be applied in cities, on websites, at conferences, or in many other contexts, if the goal is to optimize for putting up things that people want to see (or things that people want other people to see, but even here it's much more democratic than simply buying space) rather than things that wealthy people and centralized institutions want people to see.Complexities and caveatsPerhaps the biggest challenge to consider with this concept of quadratic payments is the practical implementation issue of identity and bribery/collusion. Quadratic payments in any form require a model of identity where individuals cannot easily get as many identities as they want: if they could, then they could just keep getting new identities and keep paying $1 to influence some decision as many times as they want, and the mechanism collapses into linear vote-buying. Note that the identity system does not need to be airtight (in the sense of preventing multiple-identity acquisition), and indeed there are good civil-liberties reasons why identity systems probably should not try to be airtight. Rather, it just needs to be robust enough that manipulation is not worth the cost.Collusion is also tricky. If we can't prevent people from selling their votes, the mechanisms once again collapse into one-dollar-one-vote. We don't just need votes to be anonymous and private (while still making the final result provable and public); we need votes to be so private that even the person who made the vote can't prove to anyone else what they voted for. This is difficult. Secret ballots do this well in the offline world, but secret ballots are a nineteenth century technology, far too inefficient for the sheer amount of quadratic voting and funding that we want to see in the twenty first century.Fortunately, there are technological means that can help, combining together zero-knowledge proofs, encryption and other cryptographic technologies to achieve the precise desired set of privacy and verifiability properties. There's also proposed techniques to verify that private keys actually are in an individual's possession and not in some hardware or cryptographic system that can restrict how they use those keys. However, these techniques are all untested and require quite a bit of further work.Another challenge is that quadratic payments, being a payment-based mechanism, continues to favor people with more money. Note that because the cost of votes is quadratic, this effect is dampened: someone with 100 times more money only has 10 times more influence, not 100 times, so the extent of the problem goes down by 90% (and even more for ultra-wealthy actors). That said, it may be desirable to mitigate this inequality of power further. This could be done either by denominating quadratic payments in a separate token of which everyone gets a fixed number of units, or giving each person an allocation of funds that can only be used for quadratic-payments use cases: this is basically Andrew Yang's "democracy dollars" proposal. A third challenge is the "rational ignorance" and "rational irrationality" problems, which is that decentralized public decisions have the weakness that any single individual has very little effect on the outcome, and so little motivation to make sure they are supporting the decision that is best for the long term; instead, pressures such as tribal affiliation may dominate. There are many strands of philosophy that emphasize the ability of large crowds to be very wrong despite (or because of!) their size, and quadratic payments in any form do little to address this.Quadratic payments do better at mitigating this problem than one-person-one-vote systems, and these problems can be expected to be less severe for medium-scale public goods than for large decisions that affect many millions of people, so it may not be a large challenge at first, but it's certainly an issue worth confronting. One approach is combining quadratic voting with elements of sortition. Another, potentially more long-term durable, approach is to combine quadratic voting with another economic technology that is much more specifically targeted toward rewarding the "correct contrarianism" that can dispel mass delusions: prediction markets. A simple example would be a system where quadratic funding is done retrospectively, so people vote on which public goods were valuable some time ago (eg. even 2 years), and projects are funded up-front by selling shares of the results of these deferred votes; by buying shares people would be both funding the projects and betting on which project would be viewed as successful in 2 years' time. There is a large design space to experiment with here.ConclusionAs I mentioned at the beginning, quadratic payments do not solve every problem. They solve the problem of governing resources that affect large numbers of people, but they do not solve many other kinds of problems. A particularly important one is information asymmetry and low quality of information in general. For this reason, I am a fan of techniques such as prediction markets (see electionbettingodds.com for one example) to solve information-gathering problems, and many applications can be made most effective by combining different mechanisms together.One particular cause dear to me personally is what I call "entrepreneurial public goods": public goods that in the present only a few people believe are important but in the future many more people will value. In the 19th century, contributing to abolition of slavery may have been one example; in the 21st century I can't give examples that will satisfy every reader because it's the nature of these goods that their importance will only become common knowledge later down the road, but I would point to life extension and AI risk research as two possible examples.That said, we don't need to solve every problem today. Quadratic payments are an idea that has only become popular in the last few years; we still have not seen more than small-scale trials of quadratic voting and funding, and quadratic attention payments have not been tried at all! There is still a long way to go. But if we can get these mechanisms off the ground, there is a lot that these mechanisms have to offer!
Quadratic Payments: A Primer Quadratic Payments: A Primer2019 Dec 07 See all posts Quadratic Payments: A Primer Special thanks to Karl Floersch and Jinglan Wang for feedbackIf you follow applied mechanism design or decentralized governance at all, you may have recently heard one of a few buzzwords: quadratic voting, quadratic funding and quadratic attention purchase. These ideas have been gaining popularity rapidly over the last few years, and small-scale tests have already been deployed: the Taiwanese presidential hackathon used quadratic voting to vote on winning projects, Gitcoin Grants used quadratic funding to fund public goods in the Ethereum ecosystem, and the Colorado Democratic party also experimented with quadratic voting to determine their party platform.To the proponents of these voting schemes, this is not just another slight improvement to what exists. Rather, it's an initial foray into a fundamentally new class of social technology which, has the potential to overturn how we make many public decisions, large and small. The ultimate effect of these schemes rolled out in their full form could be as deeply transformative as the industrial-era advent of mostly-free markets and constitutional democracy. But now, you may be thinking: "These are large promises. What do these new governance technologies have that justifies such claims?"Private goods, private markets...To understand what is going on, let us first consider an existing social technology: money, and property rights - the invisible social technology that generally hides behind money. Money and private property are extremely powerful social technologies, for all the reasons classical economists have been stating for over a hundred years. If Bob is producing apples, and Alice wants to buy apples, we can economically model the interaction between the two, and the results seem to make sense: Alice keeps buying apples until the marginal value of the next apple to her is less than the cost of producing it, which is pretty much exactly the optimal thing that could happen. This is all formalized in results such as the "fundamental theorems of welfare economics". Now, those of you who have learned some economics may be screaming, but what about imperfect competition? Asymmetric information? Economic inequality? Public goods? Externalities? Many activities in the real world, including those that are key to the progress of human civilization, benefit (or harm) many people in complicated ways. These activities and the consequences that arise from them often cannot be neatly decomposed into sequences of distinct trades between two parties.But since when do we expect a single package of technologies to solve every problem anyway? "What about oceans?" isn't an argument against cars, it's an argument against car maximalism, the position that we need cars and nothing else. Much like how private property and markets deal with private goods, can we try to use economic means to deduce what kind of social technologies would work well for encouraging production of the public goods that we need?... Public goods, public marketsPrivate goods (eg. apples) and public goods (eg. public parks, air quality, scientific research, this article...) are different in some key ways. When we are talking about private goods, production for multiple people (eg. the same farmer makes apples for both Alice and Bob) can be decomposed into (i) the farmer making some apples for Alice, and (ii) the farmer making some other apples for Bob. If Alice wants apples but Bob does not, then the farmer makes Alice's apples, collects payment from Alice, and leaves Bob alone. Even complex collaborations (the "I, Pencil" essay popular in libertarian circles comes to mind) can be decomposed into a series of such interactions. When we are talking about public goods, however, this kind of decomposition is not possible. When I write this blog article, it can be read by both Alice and Bob (and everyone else). I could put it behind a paywall, but if it's popular enough it will inevitably get mirrored on third-party sites, and paywalls are in any case annoying and not very effective. Furthermore, making an article available to ten people is not ten times cheaper than making the article available to a hundred people; rather, the cost is exactly the same. So I either produce the article for everyone, or I do not produce it for anyone at all.So here comes the challenge: how do we aggregate together people's preferences? Some private and public goods are worth producing, others are not. In the case of private goods, the question is easy, because we can just decompose it into a series of decisions for each individual. Whatever amount each person is willing to pay for, that much gets produced for them; the economics is not especially complex. In the case of public goods, however, you cannot "decompose", and so we need to add up people's preferences in a different way.First of all, let's see what happens if we just put up a plain old regular market: I offer to write an article as long as at least $1000 of money gets donated to me (fun fact: I literally did this back in 2011). Every dollar donated increases the probability that the goal will be reached and the article will be published; let us call this "marginal probability" p. At a cost of $k, you can increase the probability that the article will be published by k * p (though eventually the gains will decrease as the probability approaches 100%). Let's say to you personally, the article being published is worth $V. Would you donate? Well, donating a dollar increases the probability it will be published by p, and so gives you an expected $p * V of value. If p * V > 1, you donate, and quite a lot, and if p * V < 1 you don't donate at all.Phrased less mathematically, either you value the article enough (and/or are rich enough) to pay, and if that's the case it's in your interest to keep paying (and influencing) quite a lot, or you don't value the article enough and you contribute nothing. Hence, the only blog articles that get published would be articles where some single person is willing to basically pay for it themselves (in my experiment in 2011, this prediction was experimentally verified: in most rounds, over half of the total contribution came from a single donor). Note that this reasoning applies for any kind of mechanism that involves "buying influence" over matters of public concern. This includes paying for public goods, shareholder voting in corporations, public advertising, bribing politicians, and much more. The little guy has too little influence (not quite zero, because in the real world things like altruism exist) and the big guy has too much. If you had an intuition that markets work great for buying apples, but money is corrupting in "the public sphere", this is basically a simplified mathematical model that shows why.We can also consider a different mechanism: one-person-one-vote. Let's say you can either vote that I deserve a reward for writing this article, or you can vote that I don't, and my reward is proportional to the number of votes in my favor. We can interpret this as follows: your first "contribution" costs only a small amount of effort, so you'll support an article if you care about it enough, but after that point there is no more room to contribute further; your second contribution "costs" infinity. Now, you might notice that neither of the graphs above look quite right. The first graph over-privileges people who care a lot (or are wealthy), the second graph over-privileges people who care only a little, which is also a problem. The single sheep's desire to live is more important than the two wolves' desire to have a tasty dinner.But what do we actually want? Ultimately, we want a scheme where how much influence you "buy" is proportional to how much you care. In the mathematical lingo above, we want your k to be proportional to your V. But here's the problem: your V determines how much you're willing to pay for one unit of influence. If Alice were willing to pay $100 for the article if she had to fund it herself, then she would be willing to pay $1 for an increased 1% chance it will get written, and if Bob were only willing to pay $50 for the article then he would only be willing to pay $0.5 for the same "unit of influence".So how do we match these two up? The answer is clever: your n'th unit of influence costs you $n . That is, for example, you could buy your first vote for $0.01, but then your second would cost $0.02, your third $0.03, and so forth. Suppose you were Alice in the example above; in such a system she would keep buying units of influence until the cost of the next one got to $1, so she would buy 100 units. Bob would similarly buy until the cost got to $0.5, so he would buy 50 units. Alice's 2x higher valuation turned into 2x more units of influence purchased.Let's draw this as a graph: Now let's look at all three beside each other:One dollar one vote Quadratic voting One person one vote Notice that only quadratic voting has this nice property that the amount of influence you purchase is proportional to how much you care; the other two mechanisms either over-privilege concentrated interests or over-privilege diffuse interests.Now, you might ask, where does the quadratic come from? Well, the marginal cost of the n'th vote is $n (or $0.01 * n), but the total cost of n votes is \(\approx \frac\). You can view this geometrically as follows: The total cost is the area of a triangle, and you probably learned in math class that area is base * height / 2. And since here base and height are proportionate, that basically means that total cost is proportional to number of votes squared - hence, "quadratic". But honestly it's easier to think "your n'th unit of influence costs $n".Finally, you might notice that above I've been vague about what "one unit of influence" actually means. This is deliberate; it can mean different things in different contexts, and the different "flavors" of quadratic payments reflect these different perspectives.Quadratic VotingSee also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=2003531Let us begin by exploring the first "flavor" of quadratic payments: quadratic voting. Imagine that some organization is trying to choose between two choices for some decision that affects all of its members. For example, this could be a company or a nonprofit deciding which part of town to make a new office in, or a government deciding whether or not to implement some policy, or an internet forum deciding whether or not its rules should allow discussion of cryptocurrency prices. Within the context of the organization, the choice made is a public good (or public bad, depending on whom you talk to): everyone "consumes" the results of the same decision, they just have different opinions about how much they like the result.This seems like a perfect target for quadratic voting. The goal is that option A gets chosen if in total people like A more, and option B gets chosen if in total people like B more. With simple voting ("one person one vote"), the distinction between stronger vs weaker preferences gets ignored, so on issues where one side is of very high value to a few people and the other side is of low value to more people, simple voting is likely to give wrong answers. With a private-goods market mechanism where people can buy as many votes as they want at the same price per vote, the individual with the strongest preference (or the wealthiest) carries everything. Quadratic voting, where you can make n votes in either direction at a cost of n2, is right in the middle between these two extremes, and creates the perfect balance. Note that in the voting case, we're deciding two options, so different people will favor A over B or B over A; hence, unlike the graphs we saw earlier that start from zero, here voting and preference can both be positive or negative (which option is considered positive and which is negative doesn't matter; the math works out the same way)As shown above, because the n'th vote has a cost of n, the number of votes you make is proportional to how much you value one unit of influence over the decision (the value of the decision multiplied by the probability that one vote will tip the result), and hence proportional to how much you care about A being chosen over B or vice versa. Hence, we once again have this nice clean "preference adding" effect.We can extend quadratic voting in multiple ways. First, we can allow voting between more than two options. While traditional voting schemes inevitably fall prey to various kinds of "strategic voting" issues because of Arrow's theorem and Duverger's law, quadratic voting continues to be optimal in contexts with more than two choices.The intuitive argument for those interested: suppose there are established candidates A and B and new candidate C. Some people favor C > A > B but others C > B > A. in a regular vote, if both sides think C stands no chance, they decide may as well vote their preference between A and B, so C gets no votes, and C's failure becomes a self-fulfilling prophecy. In quadratic voting the former group would vote [A +10, B -10, C +1] and the latter [A -10, B +10, C +1], so the A and B votes cancel out and C's popularity shines through.Second, we can look not just at voting between discrete options, but also at voting on the setting of a thermostat: anyone can push the thermostat up or down by 0.01 degrees n times by paying a cost of n2. Plot twist: the side wanting it colder only wins when they convince the other side that "C" stands for "caliente". Quadratic fundingSee also the original paper: https://papers.ssrn.com/sol3/papers.cfm?abstract%5fid=3243656Quadratic voting is optimal when you need to make some fixed number of collective decisions. But one weakness of quadratic voting is that it doesn't come with a built-in mechanism for deciding what goes on the ballot in the first place. Proposing votes is potentially a source of considerable power if not handled with care: a malicious actor in control of it can repeatedly propose some decision that a majority weakly approves of and a minority strongly disapproves of, and keep proposing it until the minority runs out of voting tokens (if you do the math you'll see that the minority would burn through tokens much faster than the majority). Let's consider a flavor of quadratic payments that does not run into this issue, and makes the choice of decisions itself endogenous (ie. part of the mechanism itself). In this case, the mechanism is specialized for one particular use case: individual provision of public goods.Let us consider an example where someone is looking to produce a public good (eg. a developer writing an open source software program), and we want to figure out whether or not this program is worth funding. But instead of just thinking about one single public good, let's create a mechanism where anyone can raise funds for what they claim to be a public good project. Anyone can make a contribution to any project; a mechanism keeps track of these contributions and then at the end of some period of time the mechanism calculates a payment to each project. The way that this payment is calculated is as follows: for any given project, take the square root of each contributor's contribution, add these values together, and take the square of the result. Or in math speak:\[(\sum_^n \sqrt)^2\]If that sounds complicated, here it is graphically: In any case where there is more than one contributor, the computed payment is greater than the raw sum of contributions; the difference comes out of a central subsidy pool (eg. if ten people each donate $1, then the sum-of-square-roots is $10, and the square of that is $100, so the subsidy is $90). Note that if the subsidy pool is not big enough to make the full required payment to every project, we can just divide the subsidies proportionately by whatever constant makes the totals add up to the subsidy pool's budget; you can prove that this solves the tragedy-of-the-commons problem as well as you can with that subsidy budget.There are two ways to intuitively interpret this formula. First, one can look at it through the "fixing market failure" lens, a surgical fix to the tragedy of the commons problem. In any situation where Alice contributes to a project and Bob also contributes to that same project, Alice is making a contribution to something that is valuable not only to herself, but also to Bob. When deciding how much to contribute, Alice was only taking into account the benefit to herself, not Bob, whom she most likely does not even know. The quadratic funding mechanism adds a subsidy to compensate for this effect, determining how much Alice "would have" contributed if she also took into account the benefit her contribution brings to Bob. Furthermore, we can separately calculate the subsidy for each pair of people (nb. if there are N people there are N * (N-1) / 2 pairs), and add up all of these subsidies together, and give Bob the combined subsidy from all pairs. And it turns out that this gives exactly the quadratic funding formula.Second, one can look at the formula through a quadratic voting lens. We interpret the quadratic funding as being a special case of quadratic voting, where the contributors to a project are voting for that project and there is one imaginary participant voting against it: the subsidy pool. Every "project" is a motion to take money from the subsidy pool and give it to that project's creator. Everyone sending \(c_i\) of funds is making \(\sqrt\) votes, so there's a total of \(\sum_^n \sqrt\) votes in favor of the motion. To kill the motion, the subsidy pool would need to make more than \(\sum_^n \sqrt\) votes against it, which would cost it more than \((\sum_^n \sqrt)^2\). Hence, \((\sum_^n \sqrt)^2\) is the maximum transfer from the subsidy pool to the project that the subsidy pool would not vote to stop.Quadratic funding is starting to be explored as a mechanism for funding public goods already; Gitcoin grants for funding public goods in the Ethereum ecosystem is currently the biggest example, and the most recent round led to results that, in my own view, did a quite good job of making a fair allocation to support projects that the community deems valuable. Numbers in white are raw contribution totals; numbers in green are the extra subsidies. Quadratic attention paymentsSee also the original post: https://kortina.nyc/essays/speech-is-free-distribution-is-not-a-tax-on-the-purchase-of-human-attention-and-political-power/One of the defining features of modern capitalism that people love to hate is ads. Our cities have ads: Source: https://www.flickr.com/photos/argonavigo/36657795264 Our subway turnstiles have ads: Source: https://commons.wikimedia.org/wiki/File:NYC,_subway_ad_on_Prince_St.jpg Our politics are dominated by ads: Source: https://upload.wikimedia.org/wikipedia/commons/e/e3/Billboard_Challenging_the_validity_of_Barack_Obama%27s_Birth_Certificate.JPG And even the rivers and the skies have ads. Now, there are some places that seem to not have this problem: But really they just have a different kind of ads: Now, recently there are attempts to move beyond this in some cities. And on Twitter. But let's look at the problem systematically and try to see what's going wrong. The answer is actually surprisingly simple: public advertising is the evil twin of public goods production. In the case of public goods production, there is one actor that is taking on an expenditure to produce some product, and this product benefits a large number of people. Because these people cannot effectively coordinate to pay for the public goods by themselves, we get much less public goods than we need, and the ones we do get are those favored by wealthy actors or centralized authorities. Here, there is one actor that reaps a large benefit from forcing other people to look at some image, and this action harms a large number of people. Because these people cannot effectively coordinate to buy out the slots for the ads, we get ads we don't want to see, that are favored by... wealthy actors or centralized authorities.So how do we solve this dark mirror image of public goods production? With a bright mirror image of quadratic funding: quadratic fees! Imagine a billboard where anyone can pay $1 to put up an ad for one minute, but if they want to do this multiple times the prices go up: $2 for the second minute, $3 for the third minute, etc. Note that you can pay to extend the lifetime of someone else's ad on the billboard, and this also costs you only $1 for the first minute, even if other people already paid to extend the ad's lifetime many times. We can once again interpret this as being a special case of quadratic voting: it's basically the same as the "voting on a thermostat" example above, but where the thermostat in question is the number of seconds an ad stays up.This kind of payment model could be applied in cities, on websites, at conferences, or in many other contexts, if the goal is to optimize for putting up things that people want to see (or things that people want other people to see, but even here it's much more democratic than simply buying space) rather than things that wealthy people and centralized institutions want people to see.Complexities and caveatsPerhaps the biggest challenge to consider with this concept of quadratic payments is the practical implementation issue of identity and bribery/collusion. Quadratic payments in any form require a model of identity where individuals cannot easily get as many identities as they want: if they could, then they could just keep getting new identities and keep paying $1 to influence some decision as many times as they want, and the mechanism collapses into linear vote-buying. Note that the identity system does not need to be airtight (in the sense of preventing multiple-identity acquisition), and indeed there are good civil-liberties reasons why identity systems probably should not try to be airtight. Rather, it just needs to be robust enough that manipulation is not worth the cost.Collusion is also tricky. If we can't prevent people from selling their votes, the mechanisms once again collapse into one-dollar-one-vote. We don't just need votes to be anonymous and private (while still making the final result provable and public); we need votes to be so private that even the person who made the vote can't prove to anyone else what they voted for. This is difficult. Secret ballots do this well in the offline world, but secret ballots are a nineteenth century technology, far too inefficient for the sheer amount of quadratic voting and funding that we want to see in the twenty first century.Fortunately, there are technological means that can help, combining together zero-knowledge proofs, encryption and other cryptographic technologies to achieve the precise desired set of privacy and verifiability properties. There's also proposed techniques to verify that private keys actually are in an individual's possession and not in some hardware or cryptographic system that can restrict how they use those keys. However, these techniques are all untested and require quite a bit of further work.Another challenge is that quadratic payments, being a payment-based mechanism, continues to favor people with more money. Note that because the cost of votes is quadratic, this effect is dampened: someone with 100 times more money only has 10 times more influence, not 100 times, so the extent of the problem goes down by 90% (and even more for ultra-wealthy actors). That said, it may be desirable to mitigate this inequality of power further. This could be done either by denominating quadratic payments in a separate token of which everyone gets a fixed number of units, or giving each person an allocation of funds that can only be used for quadratic-payments use cases: this is basically Andrew Yang's "democracy dollars" proposal. A third challenge is the "rational ignorance" and "rational irrationality" problems, which is that decentralized public decisions have the weakness that any single individual has very little effect on the outcome, and so little motivation to make sure they are supporting the decision that is best for the long term; instead, pressures such as tribal affiliation may dominate. There are many strands of philosophy that emphasize the ability of large crowds to be very wrong despite (or because of!) their size, and quadratic payments in any form do little to address this.Quadratic payments do better at mitigating this problem than one-person-one-vote systems, and these problems can be expected to be less severe for medium-scale public goods than for large decisions that affect many millions of people, so it may not be a large challenge at first, but it's certainly an issue worth confronting. One approach is combining quadratic voting with elements of sortition. Another, potentially more long-term durable, approach is to combine quadratic voting with another economic technology that is much more specifically targeted toward rewarding the "correct contrarianism" that can dispel mass delusions: prediction markets. A simple example would be a system where quadratic funding is done retrospectively, so people vote on which public goods were valuable some time ago (eg. even 2 years), and projects are funded up-front by selling shares of the results of these deferred votes; by buying shares people would be both funding the projects and betting on which project would be viewed as successful in 2 years' time. There is a large design space to experiment with here.ConclusionAs I mentioned at the beginning, quadratic payments do not solve every problem. They solve the problem of governing resources that affect large numbers of people, but they do not solve many other kinds of problems. A particularly important one is information asymmetry and low quality of information in general. For this reason, I am a fan of techniques such as prediction markets (see electionbettingodds.com for one example) to solve information-gathering problems, and many applications can be made most effective by combining different mechanisms together.One particular cause dear to me personally is what I call "entrepreneurial public goods": public goods that in the present only a few people believe are important but in the future many more people will value. In the 19th century, contributing to abolition of slavery may have been one example; in the 21st century I can't give examples that will satisfy every reader because it's the nature of these goods that their importance will only become common knowledge later down the road, but I would point to life extension and AI risk research as two possible examples.That said, we don't need to solve every problem today. Quadratic payments are an idea that has only become popular in the last few years; we still have not seen more than small-scale trials of quadratic voting and funding, and quadratic attention payments have not been tried at all! There is still a long way to go. But if we can get these mechanisms off the ground, there is a lot that these mechanisms have to offer! -
 Christmas Special Christmas Special2019 Dec 24 See all posts Christmas Special Since it's Christmas time now, and we're theoretically supposed to be enjoying ourselves and spending time with our families instead of waging endless holy wars on Twitter, this blog post will offer some games that you can play with your friends that will help you have fun and at the same time understand some spooky mathematical concepts!1.58 dimensional chess This is a variant of chess where the board is set up like this:The board is still a normal 8x8 board, but there are only 27 open squares. The other 37 squares should be covered up by checkers or Go pieces or anything else to denote that they are inaccessible. The rules are the same as chess, with a few exceptions:White pawns move up, black pawns move left. White pawns take going left-and-up or right-and-up, black pawns take going left-and-down or left-and-up. White pawns promote upon reaching the top, black pawns promote upon reaching the left. No en passant, castling, or two-step-forward pawn jumps. Chess pieces cannot move onto or through the 37 covered squares. Knights cannot move onto the 37 covered squares, but don't care what they move "through". The game is called 1.58 dimensional chess because the 27 open squares are chosen according to a pattern based on the Sierpinski triangle. You start off with a single open square, and then every time you double the width, you take the shape at the end of the previous step, and copy it to the top left, top right and bottom left corners, but leave the bottom right corner inaccessible. Whereas in a one-dimensional structure, doubling the width increases the space by 2x, and in a two-dimensional structure, doubling the width increases the space by 4x (4 = 22), and in a three-dimensional structure, doubling the width increases the space by 8x (8 = 23), here doubling the width increases the space by 3x (3 = 21.58496), hence "1.58 dimensional" (see Hausdorff dimension for details).The game is substantially simpler and more "tractable" than full-on chess, and it's an interesting exercise in showing how in lower-dimensional spaces defense becomes much easier than offense. Note that the relative value of different pieces may change here, and new kinds of endings become possible (eg. you can checkmate with just a bishop).3 dimensional tic tac toeThe goal here is to get 4 in a straight line, where the line can go in any direction, along an axis or diagonal, including between planes. For example in this configuration X wins:It's considerably harder than traditional 2D tic tac toe, and hopefully much more fun!Modular tic-tac-toeHere, we go back down to having two dimensions, except we allow lines to wrap around:X wins Note that we allow diagonal lines with any slope, as long as they pass through all four points. Particularly, this means that lines with slope +/- 2 and +/- 1/2 are admissible:Mathematically, the board can be interpreted as a 2-dimensional vector space over integers modulo 4, and the goal being to fill in a line that passes through four points over this space. Note that there exists at least one line passing through any two points.Tic tac toe over the 4-element binary fieldHere, we have the same concept as above, except we use an even spookier mathematical structure, the 4-element field of polynomials over \(Z_2\) modulo \(x^2 + x + 1\). This structure has pretty much no reasonable geometric interpretation, so I'll just give you the addition and multiplication tables:OK fine, here are all possible lines, excluding the horizontal and the vertical lines (which are also admissible) for brevity:The lack of geometric interpretation does make the game harder to play; you pretty much have to memorize the twenty winning combinations, though note that they are basically rotations and reflections of the same four basic shapes (axial line, diagonal line, diagonal line starting in the middle, that weird thing that doesn't look like a line).Now play 1.77 dimensional connect four. I dare you.Modular pokerEveryone is dealt five (you can use whatever variant poker rules you want here in terms of how these cards are dealt and whether or not players have the right to swap cards out). The cards are interpreted as: jack = 11, queen = 12, king = 0, ace = 1. A hand is stronger than another hand, if it contains a longer sequence, with any constant difference between consecutive cards (allowing wraparound), than the other hand.Mathametically, this can be represented as, a hand is stronger if the player can come up with a line \(L(x) = mx+b\) such that they have cards for the numbers \(L(0)\), \(L(1)\) ... \(L(k)\) for the highest \(k\).Example of a full five-card winning hand. y = 4x + 5. To break ties between equal maximum-length sequences, count the number of distinct length-three sequences they have; the hand with more distinct length-three sequences wins.This hand has four length-three sequences: K 2 4, K 4 8, 2 3 4, 3 8 K. This is rare. Only consider lines of length three or higher. If a hand has three or more of the same denomination, that counts as a sequence, but if a hand has two of the same denomination, any sequences passing through that denomination only count as one sequence.This hand has no length-three sequences. If two hands are completely tied, the hand with the higher highest card (using J = 11, Q = 12, K = 0, A = 1 as above) wins.Enjoy!
Christmas Special Christmas Special2019 Dec 24 See all posts Christmas Special Since it's Christmas time now, and we're theoretically supposed to be enjoying ourselves and spending time with our families instead of waging endless holy wars on Twitter, this blog post will offer some games that you can play with your friends that will help you have fun and at the same time understand some spooky mathematical concepts!1.58 dimensional chess This is a variant of chess where the board is set up like this:The board is still a normal 8x8 board, but there are only 27 open squares. The other 37 squares should be covered up by checkers or Go pieces or anything else to denote that they are inaccessible. The rules are the same as chess, with a few exceptions:White pawns move up, black pawns move left. White pawns take going left-and-up or right-and-up, black pawns take going left-and-down or left-and-up. White pawns promote upon reaching the top, black pawns promote upon reaching the left. No en passant, castling, or two-step-forward pawn jumps. Chess pieces cannot move onto or through the 37 covered squares. Knights cannot move onto the 37 covered squares, but don't care what they move "through". The game is called 1.58 dimensional chess because the 27 open squares are chosen according to a pattern based on the Sierpinski triangle. You start off with a single open square, and then every time you double the width, you take the shape at the end of the previous step, and copy it to the top left, top right and bottom left corners, but leave the bottom right corner inaccessible. Whereas in a one-dimensional structure, doubling the width increases the space by 2x, and in a two-dimensional structure, doubling the width increases the space by 4x (4 = 22), and in a three-dimensional structure, doubling the width increases the space by 8x (8 = 23), here doubling the width increases the space by 3x (3 = 21.58496), hence "1.58 dimensional" (see Hausdorff dimension for details).The game is substantially simpler and more "tractable" than full-on chess, and it's an interesting exercise in showing how in lower-dimensional spaces defense becomes much easier than offense. Note that the relative value of different pieces may change here, and new kinds of endings become possible (eg. you can checkmate with just a bishop).3 dimensional tic tac toeThe goal here is to get 4 in a straight line, where the line can go in any direction, along an axis or diagonal, including between planes. For example in this configuration X wins:It's considerably harder than traditional 2D tic tac toe, and hopefully much more fun!Modular tic-tac-toeHere, we go back down to having two dimensions, except we allow lines to wrap around:X wins Note that we allow diagonal lines with any slope, as long as they pass through all four points. Particularly, this means that lines with slope +/- 2 and +/- 1/2 are admissible:Mathematically, the board can be interpreted as a 2-dimensional vector space over integers modulo 4, and the goal being to fill in a line that passes through four points over this space. Note that there exists at least one line passing through any two points.Tic tac toe over the 4-element binary fieldHere, we have the same concept as above, except we use an even spookier mathematical structure, the 4-element field of polynomials over \(Z_2\) modulo \(x^2 + x + 1\). This structure has pretty much no reasonable geometric interpretation, so I'll just give you the addition and multiplication tables:OK fine, here are all possible lines, excluding the horizontal and the vertical lines (which are also admissible) for brevity:The lack of geometric interpretation does make the game harder to play; you pretty much have to memorize the twenty winning combinations, though note that they are basically rotations and reflections of the same four basic shapes (axial line, diagonal line, diagonal line starting in the middle, that weird thing that doesn't look like a line).Now play 1.77 dimensional connect four. I dare you.Modular pokerEveryone is dealt five (you can use whatever variant poker rules you want here in terms of how these cards are dealt and whether or not players have the right to swap cards out). The cards are interpreted as: jack = 11, queen = 12, king = 0, ace = 1. A hand is stronger than another hand, if it contains a longer sequence, with any constant difference between consecutive cards (allowing wraparound), than the other hand.Mathametically, this can be represented as, a hand is stronger if the player can come up with a line \(L(x) = mx+b\) such that they have cards for the numbers \(L(0)\), \(L(1)\) ... \(L(k)\) for the highest \(k\).Example of a full five-card winning hand. y = 4x + 5. To break ties between equal maximum-length sequences, count the number of distinct length-three sequences they have; the hand with more distinct length-three sequences wins.This hand has four length-three sequences: K 2 4, K 4 8, 2 3 4, 3 8 K. This is rare. Only consider lines of length three or higher. If a hand has three or more of the same denomination, that counts as a sequence, but if a hand has two of the same denomination, any sequences passing through that denomination only count as one sequence.This hand has no length-three sequences. If two hands are completely tied, the hand with the higher highest card (using J = 11, Q = 12, K = 0, A = 1 as above) wins.Enjoy! -
 Review of Gitcoin Quadratic Funding Round 3 Review of Gitcoin Quadratic Funding Round 32019 Oct 24 See all posts Review of Gitcoin Quadratic Funding Round 3 Special thanks to the Gitcoin team and especially Frank Chen for working with me through these numbersThe next round of Gitcoin Grants quadratic funding has just finished, and we the numbers for how much each project has received were just released. Here are the top ten: Altogether, $163,279 was donated to 80 projects by 477 contributors, augmented by a matching pool of $100,000. Nearly half came from four contributions above $10,000: $37,500 to Lighthouse, and $12,500 each to Gas Station Network, Black Girls Code and Public Health Incentives Layer. Out of the remainder, about half came from contributions between $1,000 and $10,000, and the rest came from smaller donations of various sizes. But what matters more here are not the raw donations, but rather the subsidies that the quadratic funding mechanism applied. Gitcoin Grants is there to support valuable public goods in the Ethereum ecosystem, but also serve as a testbed for this new quadratic donation matching mechanism, and see how well it lives up to its promise of creating a democratic, market-based and efficient way of funding public goods. This time around, a modified formula based on pairwise-bounded coordination subsidies was used, which has the goal of minimizing distortion from large contributions from coordinated actors. And now we get to see how the experiment went.Judging the OutcomesFirst, the results. Ultimately, every mechanism for allocating resources, whether centralized, market-based, democratic or otherwise, must stand the test of delivering results, or else sooner or later it will be abandoned for another mechanism that is perceived to be better, even if it is less philosophically clean. Judging results is inherently a subjective exercise; any single person's analysis of a mechanism will inevitably be shaped by how well the results fit their own preferences and tastes. However, in those cases where a mechanism does output a surprising result, one can and should use that as an opportunity to learn, and see whether or not one missed some key information that other participants in the mechanism had.In my own case, I found the top results very agreeable and a quite reasonable catalogue of projects that are good for the Ethereum community. One of the disparities between these grants and the Ethereum Foundation grants is that the Ethereum Foundation grants (see recent rounds here and here) tend to overwhelmingly focus on technology with only a small section on education and community resources, whereas in the Gitcoin grants while technology still dominates, EthHub is #2 and lower down defiprime.com is #14 and cryptoeconomics.study is #17. In this case my personal opinion is that EF has made a genuine error in undervaluing grants to community/education organizations and Gitcoin's "collective instinct" is correct. Score one for new-age fancy quadratic market democracy.Another surprising result to me was Austin Griffith getting second place. I personally have never spent too much time thinking about Burner Wallet; I knew that it existed but in my mental space I did not take it too seriously, focusing instead on client development, L2 scaling, privacy and to a lesser extent smart contract wallets (the latter being a key use case of Gas Station Network at #8). After seeing Austin's impressive performance in this Gitcoin round, I asked a few people what was going on.Burner Wallet (website, explainer article) is an "insta-wallet" that's very easy to use: just load it up on your desktop or phone, and there you have it. It was used successfully at EthDenver to sell food from food trucks, and generally many people appreciate its convenience. Its main weaknesses are lower security and that one of its features, support for xDAI, is dependent on a permissioned chain.Austin's Gitcoin grant is there to fund his ongoing work, and I have heard one criticism: there's many prototypes, but comparatively few "things taken to completion". There is also the critique that as great as Austin is, it's difficult to argue that he's as important to the success of Ethereum as, say, Lighthouse and Prysmatic, though one can reply that what matters is not total value, but rather the marginal value of giving a given project or person an extra $10,000. On the whole, however, I feel like quadratic funding's (Glen would say deliberate!) tendency to select for things like Burner Wallet with populist appeal is a much needed corrective to the influence of the Ethereum tech elite (including myself!) who often value technical impressiveness and undervalue simple and quick things that make it really easy for people to participate in Ethereum. This one is slightly more ambiguous, but I'll say score two for new-age fancy quadratic market democracy.The main thing that I was disappointed the Gitcoiner-ati did not support more was Gitcoin maintenance itself. The Gitcoin Sustainability Fund only got a total $1,119 in raw contributions from 18 participants, plus a match of $202. The optional 5% tips that users could give to Gitcoin upon donating were not included into the quadratic matching calculations, but raised another ~$1,000. Given the amount of effort the Gitcoin people put in to making quadratic funding possible, this is not nearly enough; Gitcoin clearly deserves more than 0.9% of the total donations in the round. Meanwhile, the Ethereum Foundation (as well as Consensys and individual donors) have been giving grants to Gitcoin that include supporting Gitcoin itself. Hopefully in future rounds people will support Gitcoin itself too, but for now, score one for good old-fashioned EF technocracy.On the whole, quadratic funding, while still young and immature, seems to be a remarkably effective complement to the funding preferences of existing institutions, and it seems worthwhile to continue it and even increase its scope and size in the future.Pairwise-bounded quadratic funding vs traditional quadratic fundingRound 3 differs from previous rounds in that it uses a new flavor of quadratic funding, which limits the subsidy per pair of participants. For example, in traditional QF, if two people each donate $10, the subsidy would be $10, and if two people each donate $10,000, the subsidy would be $10,000. This property of traditional QF makes it highly vulnerable to collusion: two key employees of a project (or even two fake accounts owned by the same person) could each donate as much money as they have, and get back a very large subsidy. Pairwise-bounded QF computes the total subsidy to a project by looking through all pairs of contributors, and imposes a maximum bound on the total subsidy that any given pair of participants can trigger (combined across all projects). Pairwise-bounded QF also has the property that it generally penalizes projects that are dominated by large contributors: The projects that lost the most relative to traditional QF seem to be projects that have a single large contribution (or sometimes two). For example, "fuzz geth and Parity for EVM consensus bugs" got a $415 match compared to the $2000 he would have gotten in traditional QF; the decrease is explained by the fact that the contributions are dominated by two large $4500 contributions. On the other hand, cryptoeconomics.study got $1274, up nearly double from the $750 it would have gotten in traditional QF; this is explained by the large diversity of contributions that the project received and particularly the lack of large sponsors: the largest contribution to cryptoeconomics.study was $100.Another desirable property of pairwise-bounded QF is that it privileges cross-tribal projects. That is, if there are projects that group A typically supports, and projects that group B typically supports, then projects that manage to get support from both groups get a more favorable subsidy (because the pairs that go between groups are not as saturated). Has this incentive for building bridges appeared in these results?Unfortunately, my code of honor as a social scientist obliges me to report the negative result: the Ethereum community just does not yet have enough internal tribal structure for effects like this to materialize, and even when there are differences in correlations they don't seem strongly connected to higher subsidies due to pairwise-bounding. Here are the cross-correlations between who contributed to different projects: Generally, all projects are slightly positively correlated with each other, with a few exceptions with greater correlation and one exception with broad roughly zero correlation: Nori (120 in this chart). However, Nori did not do well in pairwise-bounded QF, because over 94% of its donations came from a single $5000 donation.Dominance of large projectsOne other pattern that we saw in this round is that popular projects got disproportionately large grants: To be clear, this is not just saying "more contributions, more match", it's saying "more contributions, more match per dollar contributed". Arguably, this is an intended feature of the mechanism. Projects that can get more people to donate to them represent public goods that serve a larger public, and so tragedy of the commons problems are more severe and hence contributions to them should be multiplied more to compensate. However, looking at the list, it's hard to argue that, say, Prysm ($3,848 contributed, $8,566 matched) is a more public good than Nimbus ($1,129 contributed, $496 matched; for the unaware, Prysm and Nimbus are both eth2 clients). The failure does not look too severe; on average, projects near the top do seem to serve a larger public and projects near the bottom do seem niche, but it seems clear that at least part of the disparity is not genuine publicness of the good, but rather inequality of attention. N units of marketing effort can attract attention of N people, and theoretically get N^2 resources.Of course, this could be solved via a "layer on top" venture-capital style: upstart new projects could get investors to support them, in return for a share of matched contributions received when they get large. Something like this would be needed eventually; predicting future public goods is as important a social function as predicting future private goods. But we could also consider less winner-take-all alternatives; the simplest one would be adjusting the QF formula so it uses an exponent of eg. 1.5 instead of 2. I can see it being worthwhile to try a future round of Gitcoin Grants with such a formula (\(\left(\sum_i x_i^}\right)^}\) instead of \(\left(\sum_i x_i^}\right)^2\)) to see what the results are like.Individual leverage curvesOne key question is, if you donate $1, or $5, or $100, how big an impact can you have on the amount of money that a project gets? Fortunately, we can use the data to calculate these deltas! The different lines are for different projects; supporting projects with higher existing support will lead to you getting a bigger multiplier. In all cases, the first dollar is very valuable, with a matching ratio in some cases over 100:1. But the second dollar is much less valuable, and matching ratios quickly taper off; even for the largest projects increasing one's donation from $32 to $64 will only get a 1:1 match, and anything above $100 becomes almost a straight donation with nearly no matching. However, given that it's likely possible to get legitimate-looking Github accounts on the grey market for around those costs, having a cap of a few hundred dollars on the amount of matched funds that any particular account can direct seems like a very reasonable mitigation, despite its costs in limiting the bulk of the matching effect to small-sized donations.ConclusionsOn the whole, this was by far the largest and the most data-rich Gitcoin funding round to date. It successfully attracted hundreds of contributors, reaching a size where we can finally see many significant effects in play and drown out the effects of the more naive forms of small-scale collusion. The experiment already seems to be leading to valuable information that can be used by future quadratic funding implementers to improve their quadratic funding implementations. The case of Austin Griffith is also interesting because $23,911 in funds that he received comes, in relative terms, surprisingly close to an average salary for a developer if the grants can be repeated on a regular schedule. What this means is that if Gitcoin Grants does continue operating regularly, and attracts and expands its pool of donations, we could be very close to seeing the first "quadratic freelancer" - someone directly "working for the public", funded by donations boosted by quadratic matching subsidies. And at that point we could start to see more experimentation in new forms of organization that live on top of quadratic funding gadgets as a base layer. All in all, this foretells an exciting and, err, radical public-goods funding future ahead of us.
Review of Gitcoin Quadratic Funding Round 3 Review of Gitcoin Quadratic Funding Round 32019 Oct 24 See all posts Review of Gitcoin Quadratic Funding Round 3 Special thanks to the Gitcoin team and especially Frank Chen for working with me through these numbersThe next round of Gitcoin Grants quadratic funding has just finished, and we the numbers for how much each project has received were just released. Here are the top ten: Altogether, $163,279 was donated to 80 projects by 477 contributors, augmented by a matching pool of $100,000. Nearly half came from four contributions above $10,000: $37,500 to Lighthouse, and $12,500 each to Gas Station Network, Black Girls Code and Public Health Incentives Layer. Out of the remainder, about half came from contributions between $1,000 and $10,000, and the rest came from smaller donations of various sizes. But what matters more here are not the raw donations, but rather the subsidies that the quadratic funding mechanism applied. Gitcoin Grants is there to support valuable public goods in the Ethereum ecosystem, but also serve as a testbed for this new quadratic donation matching mechanism, and see how well it lives up to its promise of creating a democratic, market-based and efficient way of funding public goods. This time around, a modified formula based on pairwise-bounded coordination subsidies was used, which has the goal of minimizing distortion from large contributions from coordinated actors. And now we get to see how the experiment went.Judging the OutcomesFirst, the results. Ultimately, every mechanism for allocating resources, whether centralized, market-based, democratic or otherwise, must stand the test of delivering results, or else sooner or later it will be abandoned for another mechanism that is perceived to be better, even if it is less philosophically clean. Judging results is inherently a subjective exercise; any single person's analysis of a mechanism will inevitably be shaped by how well the results fit their own preferences and tastes. However, in those cases where a mechanism does output a surprising result, one can and should use that as an opportunity to learn, and see whether or not one missed some key information that other participants in the mechanism had.In my own case, I found the top results very agreeable and a quite reasonable catalogue of projects that are good for the Ethereum community. One of the disparities between these grants and the Ethereum Foundation grants is that the Ethereum Foundation grants (see recent rounds here and here) tend to overwhelmingly focus on technology with only a small section on education and community resources, whereas in the Gitcoin grants while technology still dominates, EthHub is #2 and lower down defiprime.com is #14 and cryptoeconomics.study is #17. In this case my personal opinion is that EF has made a genuine error in undervaluing grants to community/education organizations and Gitcoin's "collective instinct" is correct. Score one for new-age fancy quadratic market democracy.Another surprising result to me was Austin Griffith getting second place. I personally have never spent too much time thinking about Burner Wallet; I knew that it existed but in my mental space I did not take it too seriously, focusing instead on client development, L2 scaling, privacy and to a lesser extent smart contract wallets (the latter being a key use case of Gas Station Network at #8). After seeing Austin's impressive performance in this Gitcoin round, I asked a few people what was going on.Burner Wallet (website, explainer article) is an "insta-wallet" that's very easy to use: just load it up on your desktop or phone, and there you have it. It was used successfully at EthDenver to sell food from food trucks, and generally many people appreciate its convenience. Its main weaknesses are lower security and that one of its features, support for xDAI, is dependent on a permissioned chain.Austin's Gitcoin grant is there to fund his ongoing work, and I have heard one criticism: there's many prototypes, but comparatively few "things taken to completion". There is also the critique that as great as Austin is, it's difficult to argue that he's as important to the success of Ethereum as, say, Lighthouse and Prysmatic, though one can reply that what matters is not total value, but rather the marginal value of giving a given project or person an extra $10,000. On the whole, however, I feel like quadratic funding's (Glen would say deliberate!) tendency to select for things like Burner Wallet with populist appeal is a much needed corrective to the influence of the Ethereum tech elite (including myself!) who often value technical impressiveness and undervalue simple and quick things that make it really easy for people to participate in Ethereum. This one is slightly more ambiguous, but I'll say score two for new-age fancy quadratic market democracy.The main thing that I was disappointed the Gitcoiner-ati did not support more was Gitcoin maintenance itself. The Gitcoin Sustainability Fund only got a total $1,119 in raw contributions from 18 participants, plus a match of $202. The optional 5% tips that users could give to Gitcoin upon donating were not included into the quadratic matching calculations, but raised another ~$1,000. Given the amount of effort the Gitcoin people put in to making quadratic funding possible, this is not nearly enough; Gitcoin clearly deserves more than 0.9% of the total donations in the round. Meanwhile, the Ethereum Foundation (as well as Consensys and individual donors) have been giving grants to Gitcoin that include supporting Gitcoin itself. Hopefully in future rounds people will support Gitcoin itself too, but for now, score one for good old-fashioned EF technocracy.On the whole, quadratic funding, while still young and immature, seems to be a remarkably effective complement to the funding preferences of existing institutions, and it seems worthwhile to continue it and even increase its scope and size in the future.Pairwise-bounded quadratic funding vs traditional quadratic fundingRound 3 differs from previous rounds in that it uses a new flavor of quadratic funding, which limits the subsidy per pair of participants. For example, in traditional QF, if two people each donate $10, the subsidy would be $10, and if two people each donate $10,000, the subsidy would be $10,000. This property of traditional QF makes it highly vulnerable to collusion: two key employees of a project (or even two fake accounts owned by the same person) could each donate as much money as they have, and get back a very large subsidy. Pairwise-bounded QF computes the total subsidy to a project by looking through all pairs of contributors, and imposes a maximum bound on the total subsidy that any given pair of participants can trigger (combined across all projects). Pairwise-bounded QF also has the property that it generally penalizes projects that are dominated by large contributors: The projects that lost the most relative to traditional QF seem to be projects that have a single large contribution (or sometimes two). For example, "fuzz geth and Parity for EVM consensus bugs" got a $415 match compared to the $2000 he would have gotten in traditional QF; the decrease is explained by the fact that the contributions are dominated by two large $4500 contributions. On the other hand, cryptoeconomics.study got $1274, up nearly double from the $750 it would have gotten in traditional QF; this is explained by the large diversity of contributions that the project received and particularly the lack of large sponsors: the largest contribution to cryptoeconomics.study was $100.Another desirable property of pairwise-bounded QF is that it privileges cross-tribal projects. That is, if there are projects that group A typically supports, and projects that group B typically supports, then projects that manage to get support from both groups get a more favorable subsidy (because the pairs that go between groups are not as saturated). Has this incentive for building bridges appeared in these results?Unfortunately, my code of honor as a social scientist obliges me to report the negative result: the Ethereum community just does not yet have enough internal tribal structure for effects like this to materialize, and even when there are differences in correlations they don't seem strongly connected to higher subsidies due to pairwise-bounding. Here are the cross-correlations between who contributed to different projects: Generally, all projects are slightly positively correlated with each other, with a few exceptions with greater correlation and one exception with broad roughly zero correlation: Nori (120 in this chart). However, Nori did not do well in pairwise-bounded QF, because over 94% of its donations came from a single $5000 donation.Dominance of large projectsOne other pattern that we saw in this round is that popular projects got disproportionately large grants: To be clear, this is not just saying "more contributions, more match", it's saying "more contributions, more match per dollar contributed". Arguably, this is an intended feature of the mechanism. Projects that can get more people to donate to them represent public goods that serve a larger public, and so tragedy of the commons problems are more severe and hence contributions to them should be multiplied more to compensate. However, looking at the list, it's hard to argue that, say, Prysm ($3,848 contributed, $8,566 matched) is a more public good than Nimbus ($1,129 contributed, $496 matched; for the unaware, Prysm and Nimbus are both eth2 clients). The failure does not look too severe; on average, projects near the top do seem to serve a larger public and projects near the bottom do seem niche, but it seems clear that at least part of the disparity is not genuine publicness of the good, but rather inequality of attention. N units of marketing effort can attract attention of N people, and theoretically get N^2 resources.Of course, this could be solved via a "layer on top" venture-capital style: upstart new projects could get investors to support them, in return for a share of matched contributions received when they get large. Something like this would be needed eventually; predicting future public goods is as important a social function as predicting future private goods. But we could also consider less winner-take-all alternatives; the simplest one would be adjusting the QF formula so it uses an exponent of eg. 1.5 instead of 2. I can see it being worthwhile to try a future round of Gitcoin Grants with such a formula (\(\left(\sum_i x_i^}\right)^}\) instead of \(\left(\sum_i x_i^}\right)^2\)) to see what the results are like.Individual leverage curvesOne key question is, if you donate $1, or $5, or $100, how big an impact can you have on the amount of money that a project gets? Fortunately, we can use the data to calculate these deltas! The different lines are for different projects; supporting projects with higher existing support will lead to you getting a bigger multiplier. In all cases, the first dollar is very valuable, with a matching ratio in some cases over 100:1. But the second dollar is much less valuable, and matching ratios quickly taper off; even for the largest projects increasing one's donation from $32 to $64 will only get a 1:1 match, and anything above $100 becomes almost a straight donation with nearly no matching. However, given that it's likely possible to get legitimate-looking Github accounts on the grey market for around those costs, having a cap of a few hundred dollars on the amount of matched funds that any particular account can direct seems like a very reasonable mitigation, despite its costs in limiting the bulk of the matching effect to small-sized donations.ConclusionsOn the whole, this was by far the largest and the most data-rich Gitcoin funding round to date. It successfully attracted hundreds of contributors, reaching a size where we can finally see many significant effects in play and drown out the effects of the more naive forms of small-scale collusion. The experiment already seems to be leading to valuable information that can be used by future quadratic funding implementers to improve their quadratic funding implementations. The case of Austin Griffith is also interesting because $23,911 in funds that he received comes, in relative terms, surprisingly close to an average salary for a developer if the grants can be repeated on a regular schedule. What this means is that if Gitcoin Grants does continue operating regularly, and attracts and expands its pool of donations, we could be very close to seeing the first "quadratic freelancer" - someone directly "working for the public", funded by donations boosted by quadratic matching subsidies. And at that point we could start to see more experimentation in new forms of organization that live on top of quadratic funding gadgets as a base layer. All in all, this foretells an exciting and, err, radical public-goods funding future ahead of us.