分类 科普知识 下的文章 - 六币之门

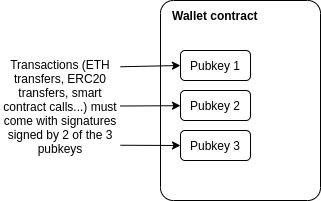
Why we need wide adoption of social recovery wallets Why we need wide adoption of social recovery wallets2021 Jan 11 See all posts Why we need wide adoption of social recovery wallets Special thanks to Itamar Lesuisse from Argent and Daniel Wang from Loopring for feedback.One of the great challenges with making cryptocurrency and blockchain applications usable for average users is security: how do we prevent users' funds from being lost or stolen? Losses and thefts are a serious issue, often costing innocent blockchain users thousands of dollars or even in some cases the majority of their entire net worth.There have been many solutions proposed over the years: paper wallets, hardware wallets, and my own one-time favorite: multisig wallets. And indeed they have led to significant improvements in security. However, these solutions have all suffered from various defects - sometimes providing far less extra protection against theft and loss than is actually needed, sometimes being cumbersome and difficult to use leading to very low adoption, and sometimes both. But recently, there is an emerging better alternative: a newer type of smart contract wallet called a social recovery wallet. These wallets can potentially provide a high level of security and much better usability than previous options, but there is still a way to go before they can be easily and widely deployed. This post will go through what social recovery wallets are, why they matter, and how we can and should move toward much broader adoption of them throughout the ecosystem.Wallet security is a really big problemWallet security issues have been a thorn in the side of the blockchain ecosystem almost since the beginning. Cryptocurrency losses and thefts were rampant even back in 2011 when Bitcoin was almost the only cryptocurrency out there; indeed, in my pre-Ethereum role as a cofounder and writer of Bitcoin Magazine, I wrote an entire article detailing the horrors of hacks and losses and thefts that were already happening at the time.Here is one sample:Last night around 9PM PDT, I clicked a link to go to CoinChat[.]freetzi[.]com – and I was prompted to run java. I did (thinking this was a legitimate chatoom), and nothing happened. I closed the window and thought nothing of it. I opened my bitcoin-qt wallet approx 14 minutes later, and saw a transaction that I did NOT approve go to wallet 1Es3QVvKN1qA2p6me7jLCVMZpQXVXWPNTC for almost my entire wallet...This person's losses were 2.07 BTC, worth $300 at the time, and over $70000 today. Here's another one:In June 2011, the Bitcointalk member "allinvain" lost 25,000 BTC (worth $500,000 at the time) after an unknown intruder somehow gained direct access to his computer. The attacker was able to access allinvain's wallet.dat file, and quickly empty out the wallet – either by sending a transaction from allinvain's computer itself, or by simply uploading the wallet.dat file and emptying it on his own machine.In present-day value, that's a loss of nearly one billion dollars. But theft is not the only concern; there are also losses from losing one's private keys. Here's Stefan Thomas:Bitcoin developer Stefan Thomas had three backups of his wallet – an encrypted USB stick, a Dropbox account and a Virtualbox virtual machine. However, he managed to erase two of them and forget the password to the third, forever losing access to 7,000 BTC (worth $125,000 at the time). Thomas's reaction: "[I'm] pretty dedicated to creating better clients since then."One analysis of the Bitcoin ecosystem suggests that 1500 BTC may be lost every day - over ten times more than what Bitcoin users spend on transaction fees, and over the years adding up to as much as 20% of the total supply. The stories and the numbers alike point to the same inescapable truth: the importance of the wallet security problem is great, and it should not be underestimated.It's easy to see the social and psychological reasons why wallet security is easy to underestimate: people naturally worry about appearing uncareful or dumb in front of an always judgemental public, and so many keep their experiences with their funds getting hacked to themselves. Loss of funds is even worse, as there is a pervasive (though in my opinion very incorrect) feeling that "there is no one to blame but yourself". But the reality is that the whole point of digital technology, blockchains included, is to make it easier for humans to engage in very complicated tasks without having to exert extreme mental effort or live in constant fear of making mistakes. An ecosystem whose only answer to losses and thefts is a combination of 12-step tutorials, not-very-secure half-measures and the not-so-occasional semi-sarcastic "sorry for your loss" is going to have a hard time getting broad adoption.So solutions that reduce the quantity of losses and thefts taking place, without requiring all cryptocurrency users to turn personal security into a full-time hobby, are highly valuable for the industry.Hardware wallets alone are not good enoughHardware wallets are often touted as the best-in-class technology for cryptocurrency funds management. A hardware wallet is a specialized hardware device which can be connected to your computer or phone (eg. through USB), and which contains a specialized chip that can only generate private keys and sign transactions. A transaction would be initiated on your computer or phone, must be confirmed on the hardware wallet before it can be sent. The private key stays on your hardware wallet, so an attacker that hacks into your computer or phone could not drain the funds.Hardware wallets are a significant improvement, and they certainly would have protected the Java chatroom victim, but they are not perfect. I see two main problems with hardware wallets:Supply chain attacks: if you buy a hardware wallet, you are trusting a number of actors that were involved in producing it - the company that designed the wallet, the factory that produced it, and everyone involved in shipping it who could have replaced it with a fake. Hardware wallets are potentially a magnet for such attacks: the ratio of funds stolen to number of devices compromised is very high. To their credit, hardware wallet manufacturers such as Ledger have put in many safeguards to protect against these risks, but some risks still remain. A hardware device fundamentally cannot be audited the same way a piece of open source software can. Still a single point of failure: if someone steals your hardware wallet right after they stand behind your shoulder and catch you typing in the PIN, they can steal your funds. If you lose your hardware wallet, then you lose your funds - unless the hardware wallet generates and outputs a backup at setup time, but as we will see those have problems of their own... Mnemonic phrases are not good enoughMany wallets, hardware and software alike, have a setup procedure during which they output a mnemonic phrase, which is a human-readable 12 to 24-word encoding of the wallet's root private key. A mnemonic phrase looks like this: vote dance type subject valley fall usage silk essay lunch endorse lunar obvious race ribbon key already arrow enable drama keen survey lesson cruelIf you lose your wallet but you have the mnemonic phrase, you can input the phrase when setting up a new wallet to recover your account, as the mnemonic phrase contains the root key from which all of your other keys can be generated.Mnemonic phrases are good for protecting against loss, but they do nothing against theft. Even worse, they add a new vector for theft: if you have the standard hardware wallet + mnemonic backup combo, then someone stealing either your hardware wallet + PIN or your mnemonic backup can steal your funds. Furthermore, maintaining a mnemonic phrase and not accidentally throwing it away is itself a non-trivial mental effort.The problems with theft can be alleviated if you split the phrase in half and give half to your friend, but (i) almost no one actually promotes this, (ii) there are security issues, as if the phrase is short (128 bits) then a sophisticated and motivated attacker who steals one piece may be able to brute-force through all \(2^\) possible combinations to find the other, and (iii) it increases the mental overhead even further.So what do we need?What we need is a wallet design which satisfies three key criteria:No single point of failure: there is no single thing (and ideally, no collection of things which travel together) which, if stolen, can give an attacker access to your funds, or if lost, can deny you access to your funds. Low mental overhead: as much as possible, it should not require users to learn strange new habits or exert mental effort to always remember to follow certain patterns of behavior. Maximum ease of transacting: most normal activities should not require much more effort than they do in regular wallets (eg. Status, Metamask...) Multisig is good!The best-in-class technology for solving these problems back in 2013 was multisig. You could have a wallet that has three keys, where any two of them are needed to send a transaction. This technology was originally developed within the Bitcoin ecosystem, but excellent multisig wallets (eg. see Gnosis Safe) now exist for Ethereum too. Multisig wallets have been highly successful within organizations: the Ethereum Foundation uses a 4-of-7 multisig wallet to store its funds, as do many other orgs in the Ethereum ecosystem.For a multisig wallet to hold the funds for an individual, the main challenge is: who holds the funds, and how are transactions approved? The most common formula is some variant of "two easily accessible, but separate, keys, held by you (eg. laptop and phone) and a third more secure but less accessible a backup, held offline or by a friend or institution".This is reasonably secure: there is no single device that can be lost or stolen that would lead to you losing access to your funds. But the security is far from perfect: if you can steal someone's laptop, it's often not that hard to steal their phone as well. The usability is also a challenge, as every transaction now requires two confirmations with two devices.Social recovery is betterThis gets us to my preferred method for securing a wallet: social recovery. A social recovery system works as follows:There is a single "signing key" that can be used to approve transactions There is a set of at least 3 (or a much higher number) of "guardians", of which a majority can cooperate to change the signing key of the account. The signing key has the ability to add or remove guardians, though only after a delay (often 1-3 days). Under all normal circumstances, the user can simply use their social recovery wallet like a regular wallet, signing messages with their signing key so that each transaction signed can fly off with a single confirmation click much like it would in a "traditional" wallet like Metamask.If a user loses their signing key, that is when the social recovery functionality would kick in. The user can simply reach out to their guardians and ask them to sign a special transaction to change the signing pubkey registered in the wallet contract to a new one. This is easy: they can simply go to a webpage such as security.loopring.io, sign in, see a recovery request and sign it. About as easy for each guardian as making a Uniswap trade.There are many possible choices for whom to select as a guardian. The three most common choices are:Other devices (or paper mnemonics) owned by the wallet holder themselves Friends and family members Institutions, which would sign a recovery message if they get a confirmation of your phone number or email or perhaps in high value cases verify you personally by video call Guardians are easy to add: you can add a guardian simply by typing in their ENS name or ETH address, though most social recovery wallets will require the guardian to sign a transaction in the recovery webpage to agree to be added. In any sanely designed social recovery wallet, the guardian does NOT need to download and use the same wallet; they can simply use their existing Ethereum wallet, whichever type of wallet it is. Given the high convenience of adding guardians, if you are lucky enough that your social circles are already made up of Ethereum users, I personally favor high guardian counts (ideally 7+) for increased security. If you already have a wallet, there is no ongoing mental effort required to be a guardian: any recovery operations that you do would be done through your existing wallet. If you not know many other active Ethereum users, then a smaller number of guardians that you trust to be technically competent is best.To reduce the risk of attacks on guardians and collusion, your guardians do not have to be publicly known: in fact, they do not need to know each other's identities. This can be accomplished in two ways. First, instead of the guardians' addresses being stored directly on chain, a hash of the list of addresses can be stored on chain, and the wallet owner would only need to publish the full list at recovery time. Second, each guardian can be asked to deterministically generate a new single-purpose address that they would use just for that particular recovery; they would not need to actually send any transactions with that address unless a recovery is actually required. To complement these technical protections, it's recommended to choose a diverse collection of guardians from different social circles (including ideally one institutional guardian); these recommendations together would make it extremely difficult for the guardians to be attacked simultaneously or collude.In the event that you die or are permanently incapacitated, it would be a socially agreed standard protocol that guardians can publicly announce themselves, so in that case they can find each other and recover your funds.Social recovery wallets are not a betrayal, but rather an expression, of "crypto values"One common response to suggestions to use any form of multisig, social recovery or otherwise, is the idea that this solution goes back to "trusting people", and so is a betrayal of the values of the blockchain and cryptocurrency industry. While I understand why one may think this at first glance, I would argue that this criticism stems from a fundamental misunderstanding of what crypto should be about.To me, the goal of crypto was never to remove the need for all trust. Rather, the goal of crypto is to give people access to cryptographic and economic building blocks that give people more choice in whom to trust, and furthermore allow people to build more constrained forms of trust: giving someone the power to do some things on your behalf without giving them the power to do everything. Viewed in this way, multisig and social recovery are a perfect expression of this principle: each participant has some influence over the ability to accept or reject transactions, but no one can move funds unilaterally. This more complex logic allows for a setup far more secure than what would be possible if there had to be one person or key that unilaterally controlled the funds.This fundamental idea, that human inputs should be wielded carefully but not thrown away outright, is powerful because it works well with the strengths and weaknesses of the human brain. The human brain is quite poorly suited for remembering passwords and tracking paper wallets, but it's an ASIC for keeping track of relationships with other people. This effect is even stronger for less technical users: they may have a harder time with wallets and passwords, but they are just as adept at social tasks like "choose 7 people who won't all gang up on me". If we can extract at least some information from human inputs into a mechanism, without those inputs turning into a vector for attack and exploitation, then we should figure out how. And social recovery is very robust: for a wallet with 7 guardians to be compromised, 4 of the 7 guardians would need to somehow discover each other and agree to steal the funds, without any of them tipping the owner off: certainly a much tougher challenge than attacking a wallet protected purely by a single individuals.How can social recovery protect against theft?Social recovery as explained above deals with the risk that you lose your wallet. But there is still the risk that your signing key gets stolen: someone hacks into your computer, sneaks up behind you while you're already logged in and hits you over the head, or even just uses some user interface glitch to trick you into signing a transaction that you did not intend to sign.We can extend social recovery to deal with such issues by adding a vault. Every social recovery wallet can come with an automatically generated vault. Assets can be moved to the vault just by sending them to the vault's address, but they can be moved out of the vault only with a 1 week delay. During that delay, the signing key (or, by extension, the guardians) can cancel the transaction. If desired, the vault could also be programmed so that some limited financial operations (eg. Uniswap trades between some whitelisted tokens) can be done without delay.Existing social recovery walletsCurrently, the two major wallets that have implemented social recovery are the Argent wallet and the Loopring wallet: The Argent wallet is the first major, and still the most popular, "smart contract wallet" currently in use, and social recovery is one of its main selling points. The Argent wallet includes an interface by which guardians can be added and removed: To protect against theft, the wallet has a daily limit: transactions up to that amount are instant but transactions above that amount require guardians to approve to finalize the withdrawal.The Loopring wallet is most known for being built by the developers of (and of course including support for) the Loopring protocol, a ZK rollup for payments and decentralized exchange. But the Loopring wallet also has a social recovery feature, which works very similarly to that in Argent. In both cases, the wallet companies provide one guardian for free, which relies on a confirmation code sent by mobile phone to authenticate you. For the other guardians, you can add either other users of the same wallet, or any Ethereum user by providing their Ethereum address.The user experience in both cases is surprisingly smooth. There were two main challenges. First, the smoothness in both cases relies on a central "relayer" run by the wallet maker that re-publishes signed messages as transactions. Second, the fees are high. Fortunately, both of these problems are surmountable.Migration to Layer 2 (rollups) can solve the remaining challengesAs mentioned above, there are two key challenges: (i) the dependence on relayers to solve transactions, and (ii) high transaction fees. The first challenge, dependence on relayers, is an increasingly common problem in Ethereum applications. The issue arises because there are two types of accounts in Ethereum: externally owned accounts (EOAs), which are accounts controlled by a single private key, and contracts. In Ethereum, there is a rule that every transaction must start from an EOA; the original intention was that EOAs represent "users" and contracts represent "applications", and an application can only run if a user talks to the application. If we want wallets with more complex policies, like multisig and social recovery, we need to use contracts to represent users. But this poses a challenge: if your funds are in a contract, you need to have some other account that has ETH that can pay to start each transaction, and it needs quite a lot of ETH just in case transaction fees get really high.Argent and Loopring get around this problem by personally running a "relayer". The relayer listens for off-chain digitally signed "messages" submitted by users, and wraps these messages in a transaction and publishes them to chain. But for the long run, this is a poor solution; it adds an extra point of centralization. If the relayer is down and a user really needs to send a transaction, they can always just send it from their own EOA, but it is nevertheless the case that a new tradeoff between centralization and inconvenience is introduced. There are efforts to solve this problem and get convenience without centralization; the main two categories revolve around either making a generalized decentralized relayer network or modifying the Ethereum protocol itself to allow transactions to begin from contracts. But neither of these solutions solve transaction fees, and in fact, they make the problem worse due to smart contracts' inherently greater complexity.Fortunately, we can solve both of these problems at the same time, by looking toward a third solution: moving the ecosystem onto layer 2 protocols such as optimistic rollups and ZK rollups. Optimistic and ZK rollups can both be designed with account abstraction built in, circumventing any need for relayers. Existing wallet developers are already looking into rollups, but ultimately migrating to rollups en masse is an ecosystem-wide challenge.An ecosystem-wide mass migration to rollups is as good an opportunity as any to reverse the Ethereum ecosystem's earlier mistakes and give multisig and smart contract wallets a much more central role in helping to secure users' funds. But this requires broader recognition that wallet security is a challenge, and that we have not gone nearly as far in trying to meet and challenge as we should. Multisig and social recovery need not be the end of the story; there may well be designs that work even better. But the simple reform of moving to rollups and making sure that these rollups treat smart contract wallets as first class citizens is an important step toward making that happen.

An approximate introduction to how zk-SNARKs are possible An approximate introduction to how zk-SNARKs are possible2021 Jan 26 See all posts An approximate introduction to how zk-SNARKs are possible Special thanks to Dankrad Feist, Karl Floersch and Hsiao-wei Wang for feedback and review.Perhaps the most powerful cryptographic technology to come out of the last decade is general-purpose succinct zero knowledge proofs, usually called zk-SNARKs ("zero knowledge succinct arguments of knowledge"). A zk-SNARK allows you to generate a proof that some computation has some particular output, in such a way that the proof can be verified extremely quickly even if the underlying computation takes a very long time to run. The "ZK" ("zero knowledge") part adds an additional feature: the proof can keep some of the inputs to the computation hidden.For example, you can make a proof for the statement "I know a secret number such that if you take the word ‘cow', add the number to the end, and SHA256 hash it 100 million times, the output starts with 0x57d00485aa". The verifier can verify the proof far more quickly than it would take for them to run 100 million hashes themselves, and the proof would also not reveal what the secret number is.In the context of blockchains, this has two very powerful applications:Scalability: if a block takes a long time to verify, one person can verify it and generate a proof, and everyone else can just quickly verify the proof instead Privacy: you can prove that you have the right to transfer some asset (you received it, and you didn't already transfer it) without revealing the link to which asset you received. This ensures security without unduly leaking information about who is transacting with whom to the public. But zk-SNARKs are quite complex; indeed, as recently as in 2014-17 they were still frequently called "moon math". The good news is that since then, the protocols have become simpler and our understanding of them has become much better. This post will try to explain how ZK-SNARKs work, in a way that should be understandable to someone with a medium level of understanding of mathematics.Note that we will focus on scalability; privacy for these protocols is actually relatively easy once the scalability is there, so we will get back to that topic at the end.Why ZK-SNARKs "should" be hardLet us take the example that we started with: we have a number (we can encode "cow" followed by the secret input as an integer), we take the SHA256 hash of that number, then we do that again another 99,999,999 times, we get the output, and we check what its starting digits are. This is a huge computation.A "succinct" proof is one where both the size of the proof and the time required to verify it grow much more slowly than the computation to be verified. If we want a "succinct" proof, we cannot require the verifier to do some work per round of hashing (because then the verification time would be proportional to the computation). Instead, the verifier must somehow check the whole computation without peeking into each individual piece of the computation.One natural technique is random sampling: how about we just have the verifier peek into the computation in 500 different places, check that those parts are correct, and if all 500 checks pass then assume that the rest of the computation must with high probability be fine, too?Such a procedure could even be turned into a non-interactive proof using the Fiat-Shamir heuristic: the prover computes a Merkle root of the computation, uses the Merkle root to pseudorandomly choose 500 indices, and provides the 500 corresponding Merkle branches of the data. The key idea is that the prover does not know which branches they will need to reveal until they have already "committed to" the data. If a malicious prover tries to fudge the data after learning which indices are going to be checked, that would change the Merkle root, which would result in a new set of random indices, which would require fudging the data again... trapping the malicious prover in an endless cycle.But unfortunately there is a fatal flaw in naively applying random sampling to spot-check a computation in this way: computation is inherently fragile. If a malicious prover flips one bit somewhere in the middle of a computation, they can make it give a completely different result, and a random sampling verifier would almost never find out. It only takes one deliberately inserted error, that a random check would almost never catch, to make a computation give a completely incorrect result.If tasked with the problem of coming up with a zk-SNARK protocol, many people would make their way to this point and then get stuck and give up. How can a verifier possibly check every single piece of the computation, without looking at each piece of the computation individually? But it turns out that there is a clever solution.PolynomialsPolynomials are a special class of algebraic expressions of the form:\(x + 5\) \(x^4\) \(x^3 + 3x^2 + 3x + 1\) \(628x^ + 318x^ + 530x^ + ... + 69x + 381\) i.e. they are a sum of any (finite!) number of terms of the form \(c x^k\).There are many things that are fascinating about polynomials. But here we are going to zoom in on a particular one: polynomials are a single mathematical object that can contain an unbounded amount of information (think of them as a list of integers and this is obvious). The fourth example above contained 816 digits of tau, and one can easily imagine a polynomial that contains far more.Furthermore, a single equation between polynomials can represent an unbounded number of equations between numbers. For example, consider the equation \(A(x) + B(x) = C(x)\). If this equation is true, then it's also true that:\(A(0) + B(0) = C(0)\) \(A(1) + B(1) = C(1)\) \(A(2) + B(2) = C(2)\) \(A(3) + B(3) = C(3)\) And so on for every possible coordinate. You can even construct polynomials to deliberately represent sets of numbers so you can check many equations all at once. For example, suppose that you wanted to check:12 + 1 = 13 10 + 8 = 18 15 + 8 = 23 15 + 13 = 28 You can use a procedure called Lagrange interpolation to construct polynomials \(A(x)\) that give (12, 10, 15, 15) as outputs at some specific set of coordinates (eg. (0, 1, 2, 3)), \(B(x)\) the outputs (1, 8, 8, 13) on those same coordinates, and so forth. In fact, here are the polynomials:\(A(x) = -2x^3 + \fracx^2 - \fracx + 12\) \(B(x) = 2x^3 - \fracx^2 + \fracx + 1\) \(C(x) = 5x + 13\) Checking the equation \(A(x) + B(x) = C(x)\) with these polynomials checks all four above equations at the same time.Comparing a polynomial to itselfYou can even check relationships between a large number of adjacent evaluations of the same polynomial using a simple polynomial equation. This is slightly more advanced. Suppose that you want to check that, for a given polynomial \(F\), \(F(x+2) = F(x) + F(x+1)\) within the integer range \(\\) (so if you also check \(F(0) = F(1) = 1\), then \(F(100)\) would be the 100th Fibonacci number).As polynomials, \(F(x+2) - F(x+1) - F(x)\) would not be exactly zero, as it could give arbitrary answers outside the range \(x = \\). But we can do something clever. In general, there is a rule that if a polynomial \(P\) is zero across some set \(S=\\) then it can be expressed as \(P(x) = Z(x) * H(x)\), where \(Z(x) =\) \((x - x_1) * (x - x_2) * ... * (x - x_n)\) and \(H(x)\) is also a polynomial. In other words, any polynomial that equals zero across some set is a (polynomial) multiple of the simplest (lowest-degree) polynomial that equals zero across that same set.Why is this the case? It is a nice corollary of polynomial long division: the factor theorem. We know that, when dividing \(P(x)\) by \(Z(x)\), we will get a quotient \(Q(x)\) and a remainer \(R(x)\) which satisfy \(P(x) = Z(x) * Q(x) + R(x)\), where the degree of the remainder \(R(x)\) is strictly less than that of \(Z(x)\). Since we know that \(P\) is zero on all of \(S\), it means that \(R\) has to be zero on all of \(S\) as well. So we can simply compute \(R(x)\) via polynomial interpolation, since it's a polynomial of degree at most \(n-1\) and we know \(n\) values (the zeroes at \(S\)). Interpolating a polynomial with all zeroes gives the zero polynomial, thus \(R(x) = 0\) and \(H(x)= Q(x)\).Going back to our example, if we have a polynomial \(F\) that encodes Fibonacci numbers (so \(F(x+2) = F(x) + F(x+1)\) across \(x = \\)), then I can convince you that \(F\) actually satisfies this condition by proving that the polynomial \(P(x) =\) \(F(x+2) - F(x+1) - F(x)\) is zero over that range, by giving you the quotient:\(H(x) = \frac\)Where \(Z(x) = (x - 0) * (x - 1) * ... * (x - 98)\).You can calculate \(Z(x)\) yourself (ideally you would have it precomputed), check the equation, and if the check passes then \(F(x)\) satisfies the condition!Now, step back and notice what we did here. We converted a 100-step-long computation (computing the 100th Fibonacci number) into a single equation with polynomials. Of course, proving the N'th Fibonacci number is not an especially useful task, especially since Fibonacci numbers have a closed form. But you can use exactly the same basic technique, just with some extra polynomials and some more complicated equations, to encode arbitrary computations with an arbitrarily large number of steps.Now, if only there was a way to verify equations with polynomials that's much faster than checking each coefficient...Polynomial commitmentsAnd once again, it turns out that there is an answer: polynomial commitments. A polynomial commitment is best viewed as a special way to "hash" a polynomial, where the hash has the additional property that you can check equations between polynomials by checking equations between their hashes. Different polynomial commitment schemes have different properties in terms of exactly what kinds of equations you can check.Here are some common examples of things you can do with various polynomial commitment schemes (we use \(com(P)\) to mean "the commitment to the polynomial \(P\)"):Add them: given \(com(P)\), \(com(Q)\) and \(com(R)\) check if \(P + Q = R\) Multiply them: given \(com(P)\), \(com(Q)\) and \(com(R)\) check if \(P * Q = R\) Evaluate at a point: given \(com(P)\), \(w\), \(z\) and a supplemental proof (or "witness") \(Q\), verify that \(P(w) = z\) It's worth noting that these primitives can be constructed from each other. If you can add and multiply, then you can evaluate: to prove that \(P(w) = z\), you can construct \(Q(x) = \frac\), and the verifier can check if \(Q(x) * (x - w) + z \stackrel P(x)\). This works because if such a polynomial \(Q(x)\) exists, then \(P(x) - z = Q(x) * (x - w)\), which means that \(P(x) - z\) equals zero at \(w\) (as \(x - w\) equals zero at \(w\)) and so \(P(x)\) equals \(z\) at \(w\).And if you can evaluate, you can do all kinds of checks. This is because there is a mathematical theorem that says, approximately, that if some equation involving some polynomials holds true at a randomly selected coordinate, then it almost certainly holds true for the polynomials as a whole. So if all we have is a mechanism to prove evaluations, we can check eg. our equation \(P(x + 2) - P(x + 1) - P(x) = Z(x) * H(x)\) using an interactive game: As I alluded to earlier, we can make this non-interactive using the Fiat-Shamir heuristic: the prover can compute r themselves by setting r = hash(com(P), com(H)) (where hash is any cryptographic hash function; it does not need any special properties). The prover cannot "cheat" by picking P and H that "fit" at that particular r but not elsewhere, because they do not know r at the time that they are picking P and H!A quick recap so farZK-SNARKs are hard because the verifier needs to somehow check millions of steps in a computation, without doing a piece of work to check each individual step directly (as that would take too long). We get around this by encoding the computation into polynomials. A single polynomial can contain an unboundedly large amount of information, and a single polynomial expression (eg. \(P(x+2) - P(x+1) - P(x) = Z(x) * H(x)\)) can "stand in" for an unboundedly large number of equations between numbers. If you can verify the equation with polynomials, you are implicitly verifying all of the number equations (replace \(x\) with any actual x-coordinate) simultaneously. We use a special type of "hash" of a polynomial, called a polynomial commitment, to allow us to actually verify the equation between polynomials in a very short amount of time, even if the underlying polynomials are very large. So, how do these fancy polynomial hashes work?There are three major schemes that are widely used at the moment: bulletproofs, Kate and FRI.Here is a description of Kate commitments by Dankrad Feist: https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html Here is a description of bulletproofs by the curve25519-dalek team: https://doc-internal.dalek.rs/bulletproofs/notes/inner_product_proof/index.html, and here is an explanation-in-pictures by myself: https://twitter.com/VitalikButerin/status/1371844878968176647 Here is a description of FRI by... myself: ../../../2017/11/22/starks_part_2.html Whoa, whoa, take it easy. Try to explain one of them simply, without shipping me off to even more scary linksTo be honest, they're not that simple. There's a reason why all this math did not really take off until 2015 or so.Please?In my opinion, the easiest one to understand fully is FRI (Kate is easier if you're willing to accept elliptic curve pairings as a "black box", but pairings are really complicated, so altogether I find FRI simpler).Here is how a simplified version of FRI works (the real protocol has many tricks and optimizations that are missing here for simplicity). Suppose that you have a polynomial \(P\) with degree \(< n\). The commitment to \(P\) is a Merkle root of a set of evaluations to \(P\) at some set of pre-selected coordinates (eg. \(\\), though this is not the most efficient choice). Now, we need to add something extra to prove that this set of evaluations actually is a degree \(< n\) polynomial.Let \(Q\) be the polynomial only containing the even coefficients of \(P\), and \(R\) be the polynomial only containing the odd coefficients of \(P\). So if \(P(x) = x^4 + 4x^3 + 6x^2 + 4x + 1\), then \(Q(x) = x^2 + 6x + 1\) and \(R(x) = 4x + 4\) (note that the degrees of the coefficients get "collapsed down" to the range \([0...\frac)\)).Notice that \(P(x) = Q(x^2) + x * R(x^2)\) (if this isn't immediately obvious to you, stop and think and look at the example above until it is).We ask the prover to provide Merkle roots for \(Q(x)\) and \(R(x)\). We then generate a random number \(r\) and ask the prover to provide a "random linear combination" \(S(x) = Q(x) + r * R(x)\).We pseudorandomly sample a large set of indices (using the already-provided Merkle roots as the seed for the randomness as before), and ask the prover to provide the Merkle branches for \(P\), \(Q\), \(R\) and \(S\) at these indices. At each of these provided coordinates, we check that:\(P(x)\) actually does equal \(Q(x^2) + x * R(x^2)\) \(S(x)\) actually does equal \(Q(x) + r * R(x)\) If we do enough checks, then we can be convinced that the "expected" values of \(S(x)\) are different from the "provided" values in at most, say, 1% of cases.Notice that \(Q\) and \(R\) both have degree \(< \frac\). Because \(S\) is a linear combination of \(Q\) and \(R\), \(S\) also has degree \(< \frac\). And this works in reverse: if we can prove \(S\) has degree \(< \frac\), then the fact that it's a randomly chosen combination prevents the prover from choosing malicious \(Q\) and \(R\) with hidden high-degree coefficients that "cancel out", so \(Q\) and \(R\) must both be degree \(< \frac\), and because \(P(x) = Q(x^2) + x * R(x^2)\), we know that \(P\) must have degree \(< n\).From here, we simply repeat the game with \(S\), progressively "reducing" the polynomial we care about to a lower and lower degree, until it's at a sufficiently low degree that we can check it directly. As in the previous examples, "Bob" here is an abstraction, useful for cryptographers to mentally reason about the protocol. In reality, Alice is generating the entire proof herself, and to prevent her from cheating we use Fiat-Shamir: we choose each randomly samples coordinate or r value based on the hash of the data generated in the proof up until that point.A full "FRI commitment" to \(P\) (in this simplified protocol) would consist of:The Merkle root of evaluations of \(P\) The Merkle roots of evaluations of \(Q\), \(R\), \(S_1\) The randomly selected branches of \(P\), \(Q\), \(R\), \(S_1\) to check \(S_1\) is correctly "reduced from" \(P\) The Merkle roots and randomly selected branches just as in steps (2) and (3) for successively lower-degree reductions \(S_2\) reduced from \(S_1\), \(S_3\) reduced from \(S_2\), all the way down to a low-degree \(S_k\) (this gets repeated \(\approx log_2(n)\) times in total) The full Merkle tree of the evaluations of \(S_k\) (so we can check it directly) Each step in the process can introduce a bit of "error", but if you add enough checks, then the total error will be low enough that you can prove that \(P(x)\) equals a degree \(< n\) polynomial in at least, say, 80% of positions. And this is sufficient for our use cases. If you want to cheat in a zk-SNARK, you would need to make a polynomial commitment for a fractional expression (eg. to "prove" the false claim that \(x^2 + 2x + 3\) evaluated at \(4\) equals \(5\), you would need to provide a polynomial commitment for \(\frac = x + 6 + \frac\)). The set of evaluations for such a fractional expression would differ from the evaluations for any real degree \(< n\) polynomial in so many positions that any attempt to make a FRI commitment to them would fail at some step.Also, you can check carefully that the total number and size of the objects in the FRI commitment is logarithmic in the degree, so for large polynomials, the commitment really is much smaller than the polynomial itself.To check equations between different polynomial commitments of this type (eg. check \(A(x) + B(x) = C(x)\) given FRI commitments to \(A\), \(B\) and \(C\)), simply randomly select many indices, ask the prover for Merkle branches at each of those indices for each polynomial, and verify that the equation actually holds true at each of those positions.The above description is a highly inefficient protocol; there is a whole host of algebraic tricks that can increase its efficiency by a factor of something like a hundred, and you need these tricks if you want a protocol that is actually viable for, say, use inside a blockchain transaction. In particular, for example, \(Q\) and \(R\) are not actually necessary, because if you choose your evaluation points very cleverly, you can reconstruct the evaluations of \(Q\) and \(R\) that you need directly from evaluations of \(P\). But the above description should be enough to convince you that a polynomial commitment is fundamentally possible.Finite fieldsIn the descriptions above, there was a hidden assumption: that each individual "evaluation" of a polynomial was small. But when we are dealing with polynomials that are big, this is clearly not true. If we take our example from above, \(628x^ + 318x^ + 530x^ + ... + 69x + 381\), that encodes 816 digits of tau, and evaluate it at \(x=1000\), you get.... an 816-digit number containing all of those digits of tau. And so there is one more thing that we need to add. In a real implementation, all of the arithmetic that we are doing here would not be done using "regular" arithmetic over real numbers. Instead, it would be done using modular arithmetic.We redefine all of our arithmetic operations as follows. We pick some prime "modulus" p. The % operator means "take the remainder of": \(15\ \%\ 7 = 1\), \(53\ \%\ 10 = 3\), etc (note that the answer is always non-negative, so for example \(-1\ \%\ 10 = 9\)). We redefine\(x + y \Rightarrow (x + y)\) % \(p\)\(x * y \Rightarrow (x * y)\) % \(p\)\(x^y \Rightarrow (x^y)\) % \(p\)\(x - y \Rightarrow (x - y)\) % \(p\)\(x / y \Rightarrow (x * y ^)\) % \(p\)The above rules are all self-consistent. For example, if \(p = 7\), then:\(5 + 3 = 1\) (as \(8\) % \(7 = 1\)) \(1 - 3 = 5\) (as \(-2\) % \(7 = 5\)) \(2 \cdot 5 = 3\) \(3 / 5 = 2\) (as (\(3 \cdot 5^5\)) % \(7 = 9375\) % \(7 = 2\)) More complex identities such as the distributive law also hold: \((2 + 4) \cdot 3\) and \(2 \cdot 3 + 4 \cdot 3\) both evaluate to \(4\). Even formulas like \((a^2 - b^2)\) = \((a - b) \cdot (a + b)\) are still true in this new kind of arithmetic.Division is the hardest part; we can't use regular division because we want the values to always remain integers, and regular division often gives non-integer results (as in the case of \(3/5\)). We get around this problem using Fermat's little theorem, which states that for any nonzero \(x < p\), it holds that \(x^\) % \(p = 1\). This implies that \(x^\) gives a number which, if multiplied by \(x\) one more time, gives \(1\), and so we can say that \(x^\) (which is an integer) equals \(\frac\). A somewhat more complicated but faster way to evaluate this modular division operator is the extended Euclidean algorithm, implemented in python here. Because of how the numbers "wrap around", modular arithmetic is sometimes called "clock math"With modular math we've created an entirely new system of arithmetic, and it's self-consistent in all the same ways traditional arithmetic is self-consistent. Hence, we can talk about all of the same kinds of structures over this field, including polynomials, that we talk about in "regular math". Cryptographers love working in modular math (or, more generally, "finite fields") because there is a bound on the size of a number that can arise as a result of any modular math calculation - no matter what you do, the values will not "escape" the set \(\\). Even evaluating a degree-1-million polynomial in a finite field will never give an answer outside that set.What's a slightly more useful example of a computation being converted into a set of polynomial equations?Let's say we want to prove that, for some polynomial \(P\), \(0 \le P(n) < 2^\), without revealing the exact value of \(P(n)\). This is a common use case in blockchain transactions, where you want to prove that a transaction leaves a balance non-negative without revealing what that balance is.We can construct a proof for this with the following polynomial equations (assuming for simplicity \(n = 64\)):\(P(0) = 0\) \(P(x+1) = P(x) * 2 + R(x)\) across the range \(\\) \(R(x) \in \\) across the range \(\\) The latter two statements can be restated as "pure" polynomial equations as follows (in this context \(Z(x) = (x - 0) * (x - 1) * ... * (x - 63)\)):\(P(x+1) - P(x) * 2 - R(x) = Z(x) * H_1(x)\) \(R(x) * (1 - R(x)) = Z(x) * H_2(x)\) (notice the clever trick: \(y * (1-y) = 0\) if and only if \(y \in \\)) The idea is that successive evaluations of \(P(i)\) build up the number bit-by-bit: if \(P(4) = 13\), then the sequence of evaluations going up to that point would be: \(\\). In binary, 1 is 1, 3 is 11, 6 is 110, 13 is 1101; notice how \(P(x+1) = P(x) * 2 + R(x)\) keeps adding one bit to the end as long as \(R(x)\) is zero or one. Any number within the range \(0 \le x < 2^\) can be built up over 64 steps in this way, any number outside that range cannot.PrivacyBut there is a problem: how do we know that the commitments to \(P(x)\) and \(R(x)\) don't "leak" information that allows us to uncover the exact value of \(P(64)\), which we are trying to keep hidden?There is some good news: these proofs are small proofs that can make statements about a large amount of data and computation. So in general, the proof will very often simply not be big enough to leak more than a little bit of information. But can we go from "only a little bit" to "zero"? Fortunately, we can.Here, one fairly general trick is to add some "fudge factors" into the polynomials. When we choose \(P\), add a small multiple of \(Z(x)\) into the polynomial (that is, set \(P'(x) = P(x) + Z(x) * E(x)\) for some random \(E(x)\)). This does not affect the correctness of the statement (in fact, \(P'\) evaluates to the same values as \(P\) on the coordinates that "the computation is happening in", so it's still a valid transcript), but it can add enough extra "noise" into the commitments to make any remaining information unrecoverable. Additionally, in the case of FRI, it's important to not sample random points that are within the domain that computation is happening in (in this case \(\\)).Can we have one more recap, please??The three most prominent types of polynomial commitments are FRI, Kate and bulletproofs. Kate is the simplest conceptually but depends on the really complicated "black box" of elliptic curve pairings. FRI is cool because it relies only on hashes; it works by successively reducing a polynomial to a lower and lower-degree polynomial and doing random sample checks with Merkle branches to prove equivalence at each step. To prevent the size of individual numbers from blowing up, instead of doing arithmetic and polynomials over the integers, we do everything over a finite field (usually integers modulo some prime p) Polynomial commitments lend themselves naturally to privacy preservation because the proof is already much smaller than the polynomial, so a polynomial commitment can't reveal more than a little bit of the information in the polynomial anyway. But we can add some randomness to the polynomials we're committing to to reduce the information revealed from "a little bit" to "zero". What research questions are still being worked on?Optimizing FRI: there are already quite a few optimizations involving carefully selected evaluation domains, "DEEP-FRI", and a whole host of other tricks to make FRI more efficient. Starkware and others are working on this. Better ways to encode computation into polynomials: figuring out the most efficient way to encode complicated computations involving hash functions, memory access and other features into polynomial equations is still a challenge. There has been great progress on this (eg. see PLOOKUP), but we still need more, especially if we want to encode general-purpose virtual machine execution into polynomials. Incrementally verifiable computation: it would be nice to be able to efficiently keep "extending" a proof while a computation continues. This is valuable in the "single-prover" case, but also in the "multi-prover" case, particularly a blockchain where a different participant creates each block. See Halo for some recent work on this. I wanna learn more!My materialsSTARKs: part 1, part 2, part 3 Specific protocols for encoding computation into polynomials: PLONK Some key mathematical optimizations I didn't talk about here: Fast Fourier transforms Other people's materialsStarkware's online course Dankrad Feist on Kate commitments Bulletproofs

Prediction Markets: Tales from the Election Prediction Markets: Tales from the Election2021 Feb 18 See all posts Prediction Markets: Tales from the Election Special thanks to Jeff Coleman, Karl Floersch and Robin Hanson for critical feedback and review.Trigger warning: I express some political opinions.Prediction markets are a subject that has interested me for many years. The idea of allowing anyone in the public to make bets about future events, and using the odds at which these bets are made as a credibly neutral source of predicted probabilities of these events, is a fascinating application of mechanism design. Closely related ideas, like futarchy, have always interested me as innovative tools that could improve governance and decision-making. And as Augur and Omen, and more recently PolyMarket, have shown, prediction markets are a fascinating application of blockchains (in all three cases, Ethereum) as well.And the 2020 US presidential election, it seems like prediction markets are finally entering the limelight, with blockchain-based markets in particular growing from near-zero in 2016 to millions of dollars of volume in 2020. As someone who is closely interested in seeing Ethereum applications cross the chasm into widespread adoption, this of course aroused my interest. At first, I was inclined to simply watch, and not participate myself: I am not an expert on US electoral politics, so why should I expect my opinion to be more correct than that of everyone else who was already trading? But in my Twitter-sphere, I saw more and more arguments from Very Smart People whom I respected arguing that the markets were in fact being irrational and I should participate and bet against them if I can. Eventually, I was convinced.I decided to make an experiment on the blockchain that I helped to create: I bought $2,000 worth of NTRUMP (tokens that pay $1 if Trump loses) on Augur. Little did I know then that my position would eventually increase to $308,249, earning me a profit of over $56,803, and that I would make all of these remaining bets, against willing counterparties, after Trump had already lost the election. What would transpire over the next two months would prove to be a fascinating case study in social psychology, expertise, arbitrage, and the limits of market efficiency, with important ramifications to anyone who is deeply interested in the possibilities of economic institution design.Before the Election My first bet on this election was actually not on a blockchain at all. When Kanye announced his presidential bid in July, a political theorist whom I ordinarily quite respect for his high-quality and original thinking immediately claimed on Twitter that he was confident that this would split the anti-Trump vote and lead to a Trump victory. I remember thinking at the time that this particular opinion of his was over-confident, perhaps even a result of over-internalizing the heuristic that if a viewpoint seems clever and contrarian then it is likely to be correct. So of course I offered to make a $200 bet, myself betting the boring conventional pro-Biden view, and he honorably accepted.The election came up again on my radar in September, and this time it was the prediction markets that caught my attention. The markets gave Trump a nearly 50% chance of winning, but I saw many Very Smart People in my Twitter-sphere whom I respected pointing out that this number seemed far too high. This of course led to the familiar "efficient markets debate": if you can buy a token that gives you $1 if Trump loses for $0.52, and Trump's actual chance of losing is much higher, why wouldn't people just come in and buy the token until the price rises more? And if nobody has done this, who are you to think that you're smarter than everyone else?Ne0liberal's Twitter thread just before Election Day does an excellent job summarizing his case against prediction markets being accurate at that time. In short, the (non-blockchain) prediction markets that most people used at least prior to 2020 have all sorts of restrictions that make it difficult for people to participate with more than a small amount of cash. As a result, if a very smart individual or a professional organization saw a probability that they believed was wrong, they would only have a very limited ability to push the price in the direction that they believe to be correct.The most important restrictions that the paper points out are:Low limits (well under $1,000) on how much each person can bet High fees (eg. a 5% withdrawal fee on PredictIt) And this is where I pushed back against ne0liberal in September: although the stodgy old-world centralized prediction markets may have low limits and high fees, the crypto markets do not! On Augur or Omen, there's no limit to how much someone can buy or sell if they think the price of some outcome token is too low or too high. And the blockchain-based prediction markets were following the same prices as PredictIt. If the markets really were over-estimating Trump because high fees and low trading limits were preventing the more cool-headed traders from outbidding the overly optimistic ones, then why would blockchain-based markets, which don't have those issues, show the same prices? PredictIt Augur The main response my Twitter friends gave to this was that blockchain-based markets are highly niche, and very few people, particularly very few people who know much about politics, have easy access to cryptocurrency. That seemed plausible, but I was not too confident in that argument. And so I bet $2,000 against Trump and went no further.The ElectionThen the election happened. After an initial scare where Trump at first won more seats than we expected, Biden turned out to be the eventual winner. Whether or not the election itself validated or refuted the efficiency of prediction markets is a topic that, as far as I can tell, is quite open to interpretation. On the one hand, by a standard Bayes rule application, I should decrease my confidence of prediction markets, at least relative to Nate Silver. Prediction markets gave a 60% chance of Biden winning, Nate Silver gave a 90% chance of Biden winning. Since Biden in fact won, this is one piece of evidence that I live in a world where Nate gives the more correct answers.But on the other hand, you can make a case that the prediction markets bettter estimated the margin of victory. The median of Nate's probability distribution was somewhere around 370 of 538 electoral college votes going to Biden: The Trump markets didn't give a probability distribution, but if you had to guess a probability distribution from the statistic "40% chance Trump will win", you would probably give one with a median somewhere around 300 EC votes for Biden. The actual result: 306. So the net score for prediction markets vs Nate seems to me, on reflection, ambiguous.After the electionBut what I could not have imagined at the time was that the election itself was just the beginning. A few days after the election, Biden was declared the winner by various major organizations and even a few foreign governments. Trump mounted various legal challenges to the election results, as was expected, but each of these challenges quickly failed. But for over a month, the price of the NTRUMP tokens stayed at 85 cents!At the beginning, it seemed reasonable to guess that Trump had a 15% chance of overturning the results; after all, he had appointed three judges to the Supreme Court, at a time of heightened partisanship where many have come to favor team over principle. Over the next three weeks, however, it became more and more clear that the challenges were failing, and Trump's hopes continued to look grimmer with each passing day, but the NTRUMP price did not budge; in fact, it even briefly decreased to around $0.82. On December 11, more than five weeks after the election, the Supreme Court decisively and unanimously rejected Trump's attempts to overturn the vote, and the NTRUMP price finally rose.... to $0.88.It was in November that I was finally convinced that the market skeptics were right, and I plunged in and bet against Trump myself. The decision was not so much about the money; after all, barely two months later I would earn and donate to GiveDirectly a far larger amount simply from holding dogecoin. Rather, it was to take part in the experiment not just as an observer, but as an active participant, and improve my personal understanding of why everyone else hadn't already plunged in to buy NTRUMP tokens before me.Dipping inI bought my NTRUMP on Catnip, a front-end user interface that combines together the Augur prediction market with Balancer, a Uniswap-style constant-function market maker. Catnip was by far the easiest interface for making these trades, and in my opinion contributed significantly to Augur's usability.There are two ways to bet against Trump with Catnip:Use DAI to buy NTRUMP on Catnip directly Use Foundry to access an Augur feature that allows you to convert 1 DAI into 1 NTRUMP + 1 YTUMP + 1ITRUMP (the "I" stands for "invalid", more on this later), and sell the YTRUMP on Catnip At first, I only knew about the first option. But then I discovered that Balancer has far more liquidity for YTRUMP, and so I switched to the second option.There was also another problem: I did not have any DAI. I had ETH, and I could have sold my ETH to get DAI, but I did not want to sacrifice my ETH exposure; it would have been a shame if I earned $50,000 betting against Trump but simultaneously lost $500,000 missing out on ETH price changes. So I decided to keep my ETH price exposure the same by opening up a collateralized debt position (CDP, now also called a "vault") on MakerDAO.A CDP is how all DAI is generated: users deposit their ETH into a smart contract, and are allowed to withdraw an amount of newly-generated DAI up to 2/3 of the value of ETH that they put in. They can get their ETH back by sending back the same amount of DAI that they withdrew plus an extra interest fee (currently 3.5%). If the value of the ETH collateral that you deposited drops to less than 150% the value of the DAI you withdrew, anyone can come in and "liquidate" the vault, forcibly selling the ETH to buy back the DAI and charging you a high penalty. Hence, it's a good idea to have a high collateralization ratio in case of sudden price movements; I had over $3 worth of ETH in my CDP for every $1 that I withdrew.Recapping the above, here's the pipeline in diagram form: I did this many times; the slippage on Catnip meant that I could normally make trades only up to about $5,000 to $10,000 at a time without prices becoming too unfavorable (when I had skipped Foundry and bought NTRUMP with DAI directly, the limit was closer to $1,000). And after two months, I had accumulated over 367,000 NTRUMP.Why not everyone else?Before I went in, I had four main hypotheses about why so few others were buying up dollars for 85 cents:Fear that either the Augur smart contracts would break or Trump supporters would manipulate the oracle (a decentralized mechanism where holders of Augur's REP token vote by staking their tokens on one outcome or the other) to make it return a false result Capital costs: to buy these tokens, you have to lock up funds for over two months, and this removes your ability to spend those funds or make other profitable trades for that duration It's too technically complicated for almost everyone to trade There just really are far fewer people than I thought who are actually motivated enough to take a weird opportunity even when it presents them straight in the face All four have reasonable arguments going for them. Smart contracts breaking is a real risk, and the Augur oracle had not before been tested in such a contentious environment. Capital costs are real, and while betting against something is easier in a prediction market than in a stock market because you know that prices will never go above $1, locking up capital nevertheless competes with other lucrative opportunities in the crypto markets. Making transactions things in dapps is technically complicated, and it's rational to have some degree of fear-of-the-unknown.But my experience actually going into the financial trenches, and watching the prices on this market evolve, taught me a lot about each of these hypotheses.Fear of smart contract exploitsAt first, I thought that "fear of smart contract exploits" must have been a significant part of the explanation. But over time, I have become more convinced that it is probably not a dominant factor. One way to see why I think this is the case is to compare the prices for YTRUMP and ITRUMP. ITRUMP stands for "Invalid Trump"; "Invalid" is an event outcome that is intended to be triggered in some exceptional cases: when the description of the event is ambiguous, when the outcome of the event is not yet known when the market is resolved, when the market is unethical (eg. assassination markets), and a few other similar situations. In this market, the price of ITRUMP consistently stayed under $0.02. If someone wanted to earn a profit by attacking the market, it would be far more lucrative for them to not buy YTRUMP at $0.15, but instead buy ITRUMP at $0.02. If they buy a large amount of ITRUMP, they could earn a 50x return if they can force the "invalid" outcome to actually trigger. So if you fear an attack, buying ITRUMP is by far the most rational response. And yet, very few people did.A further argument against fear of smart contract exploits, of course, is the fact that in every crypto application except prediction markets (eg. Compound, the various yield farming schemes) people are surprisingly blasé about smart contract risks. If people are willing to put their money into all sorts of risky and untested schemes even for a promise of mere 5-8% annual gains, why would they suddenly become over-cautious here?Capital costsCapital costs - the inconvenience and opportunity cost of locking up large amounts of money - are a challenge that I have come to appreciate much more than I did before. Just looking at the Augur side of things, I needed to lock up 308,249 DAI for an average of about two months to make a $56,803 profit. This works out to about a 175% annualized interest rate; so far, quite a good deal, even compared to the various yield farming crazes of the summer of 2020. But this becomes worse when you take into account what I needed to do on MakerDAO. Because I wanted to keep my exposure to ETH the same, I needed to get my DAI through a CDP, and safely using a CDP required a collateral ratio of over 3x. Hence, the total amount of capital I actually needed to lock up was somewhere around a million dollars. Now, the interest rates are looking less favorable. And if you add to that the possibility, however remote, that a smart contract hack, or a truly unprecedented political event, actually will happen, it looks less favorable still.But even still, assuming a 3x lockup and a 3% chance of Augur breaking (I had bought ITRUMP to cover the possibility that it breaks in the "invalid" direction, so I needed only worry about the risk of breaks in the "yes" direction or the the funds being stolen outright), that works out to a risk-neutral rate of about 35%, and even lower once you take real human beings' views on risk into account. The deal is still very attractive, but on the other hand, it now looks very understandable that such numbers are unimpressive to people who live and breathe cryptocurrency with its frequent 100x ups and downs.Trump supporters, on the other hand, faced none of these challenges: they cancelled out my $308,249 bet by throwing in a mere $60,000 (my winnings are less than this because of fees). When probabilities are close to 0 or 1, as is the case here, the game is very lopsided in favor of those who are trying to push the probability away from the extreme value. And this explains not just Trump; it's also the reason why all sorts of popular-among-a-niche candidates with no real chance of victory frequently get winning probabilities as high as 5%.Technical complexityI had at first tried buying NTRUMP on Augur, but technical glitches in the user interface prevented me from being able to make orders on Augur directly (other people I talked to did not have this issue... I am still not sure what happened there). Catnip's UI is much simpler and worked excellently. However, automated market makers like Balancer (and Uniswap) work best for smaller trades; for larger trades, the slippage is too high. This is a good microcosm of the broader "AMM vs order book" debate: AMMs are more convenient but order books really do work better for large trades. Uniswap v3 is introducing an AMM design that has better capital efficiency; we shall see if that improves things.There were other technical complexities too, though fortunately they all seem to be easily solvable. There is no reason why an interface like Catnip could not integrate the "DAI -> Foundry -> sell YTRUMP" path into a contract so that you could buy NTRUMP that way in a single transaction. In fact, the interface could even check the price and liquidity properties of the "DAI -> NTRUMP" path and the "DAI -> Foundry -> sell YTRUMP" path and give you the better trade automatically. Even withdrawing DAI from a MakerDAO CDP can be included in that path. My conclusion here is optimistic: technical complexity issues were a real barrier to participation this round, but things will be much easier in future rounds as technology improves.Intellectual underconfidenceAnd now we have the final possibility: that many people (and smart people in particular) have a pathology that they suffer from excessive humility, and too easily conclude that if no one else has taken some action, then there must therefore be a good reason why that action is not worth taking.Eliezer Yudkowsky spends the second half of his excellent book Inadequate Equilibria making this case, arguing that too many people overuse "modest epistemology", and we should be much more willing to act on the results of our reasoning, even when the result suggests that the great majority of the population is irrational or lazy or wrong about something. When I read those sections for the first time, I was unconvinced; it seemed like Eliezer was simply being overly arrogant. But having gone through this experience, I have come to see some wisdom in his position.This was not my first time seeing the virtues of trusting one's own reasoning first hand. When I had originally started working on Ethereum, I was at first beset by fear that there must be some very good reason the project was doomed to fail. A fully programmable smart-contract-capable blockchain, I reasoned, was clearly such a great improvement over what came before, that surely many other people must have thought of it before I did. And so I fully expected that, as soon as I publish the idea, many very smart cryptographers would tell me the very good reasons why something like Ethereum was fundamentally impossible. And yet, no one ever did.Of course, not everyone suffers from excessive modesty. Many of the people making predictions in favor of Trump winning the election were arguably fooled by their own excessive contrarianism. Ethereum benefited from my youthful suppression of my own modesty and fears, but there are plenty of other projects that could have benefited from more intellectual humility and avoided failures. Not a sufferer of excessive modesty.But nevertheless it seems to me more true than ever that, as goes the famous Yeats quote, "the best lack all conviction, while the worst are full of passionate intensity." Whatever the faults of overconfidence or contrarianism sometimes may be, it seems clear to me that spreading a society-wide message that the solution is to simply trust the existing outputs of society, whether those come in the form of academic institutions, media, governments or markets, is not the solution. All of these institutions can only work precisely because of the presence of individuals who think that they do not work, or who at least think that they can be wrong at least some of the time.Lessons for futarchySeeing the importance of capital costs and their interplay with risks first hand is also important evidence for judging systems like futarchy. Futarchy, and "decision markets" more generally are an important and potentially very socially useful application of prediction markets. There is not much social value in having slightly more accurate predictions of who will be the next president. But there is a lot of social value in having conditional predictions: if we do A, what's the chance it will lead to some good thing X, and if we do B instead what are the chances then? Conditional predictions are important because they do not just satisfy our curiosity; they can also help us make decisions.Though electoral prediction markets are much less useful than conditional predictions, they can help shed light on an important question: how robust are they to manipulation or even just biased and wrong opinions? We can answer this question by looking at how difficult arbitrage is: suppose that a conditional prediction market currently gives probabilities that (in your opinion) are wrong (could be because of ill-informed traders or an explicit manipulation attempt; we don't really care). How much of an impact can you have, and how much profit can you make, by setting things right?Let's start with a concrete example. Suppose that we are trying to use a prediction market to choose between decision A and decision B, where each decision has some probability of achieving some desirable outcome. Suppose that your opinion is that decision A has a 50% chance of achieving the goal, and decision B has a 45% chance. The market, however, (in your opinion wrongly) thinks decision B has a 55% chance and decision A has a 40% chance.Probability of good outcome if we choose strategy... Current market position Your opinion A 40% 50% B 55% 45% Suppose that you are a small participant, so your individual bets won't affect the outcome; only many bettors acting together could. How much of your money should you bet?The standard theory here relies on the Kelly criterion. Essentially, you should act to maximize the expected logarithm of your assets. In this case, we can solve the resulting equation. Suppose you invest portion \(r\) of your money into buying A-token for $0.4. Your expected new log-wealth, from your point of view, would be:\(0.5 * log((1-r) + \frac) + 0.5 * log(1-r)\)The first term is the 50% chance (from your point of view) that the bet pays off, and the portion \(r\) that you invest grows by 2.5x (as you bought dollars at 40 cents). The second term is the 50% chance that the bet does not pay off, and you lose the portion you bet. We can use calculus to find the \(r\) that maximizes this; for the lazy, here's WolframAlpha. The answer is \(r = \frac\). If other people buy and the price for A on the market gets up to 47% (and B gets down to 48%), we can redo the calculation for the last trader who would flip the market over to make it correctly favor A:\(0.5 * log((1-r) + \frac) + 0.5 * log(1-r)\)Here, the expected-log-wealth-maximizing \(r\) is a mere 0.0566. The conclusion is clear: when decisions are close and when there is a lot of noise, it turns out that it only makes sense to invest a small portion of your money in a market. And this is assuming rationality; most people invest less into uncertain gambles than the Kelly criterion says they should. Capital costs stack on top even further. But if an attacker really wants to force outcome B through because they want it to happen for personal reasons, they can simply put all of their capital toward buying that token. All in all, the game can easily be lopsided more than 20:1 in favor of the attacker.Of course, in reality attackers are rarely willing to stake all their funds on one decision. And futarchy is not the only mechanism that is vulerable to attacks: stock markets are similarly vulnerable, and non-market decision mechanisms can also be manipulated by determined wealthy attackers in all sorts of ways. But nevertheless, we should be wary of assuming that futarchy will propel us to new heights of decision-making accuracy.Interestingly enough, the math seems to suggest that futarchy would work best when the expected manipulators would want to push the outcome toward an extreme value. An example of this might be liability insurance, as someone wishing to improperly obtain insurance would effectively be trying to force the market-estimated probability that an unfavorable event will happen down to zero. And as it turns out, liability insurance is futarchy inventor Robin Hanson's new favorite policy prescription.Can prediction markets become better?The final question to ask is: are prediction markets doomed to repeat errors as grave as giving Trump a 15% chance of overturning the election in early December, and a 12% chance of overturning it even after the Supreme Court including three judges whom he appointed telling him to screw off? Or could the markets improve over time? My answer is, surprisingly, emphatically on the optimistic side, and I see a few reasons for optimism.Markets as natural selectionFirst, these events have given me a new perspective on how market efficiency and rationality might actually come about. Too often, proponents of market efficiency theories claim that market efficiency results because most participants are rational (or at least the rationals outweigh any coherent group of deluded people), and this is true as an axiom. But instead, we could take an evolutionary perspective on what is going on.Crypto is a young ecosystem. It is an ecosystem that is still quite disconnected from the mainstream, Elon's recent tweets notwithstanding, and that does not yet have much expertise in the minutiae of electoral politics. Those who are experts in electoral politics have a hard time getting into crypto, and crypto has a large presence of not-always-correct forms of contrarianism especially when it comes to politics. But what happened this year is that within the crypto space, prediction market users who correctly expected Biden to win got an 18% increase to their capital, and prediction market users who incorrectly expected Trump to win got a 100% decrease to their capital (or at least the portion they put into the bet). Thus, there is a selection pressure in favor of the type of people who make bets that turn out to be correct. After ten rounds of this, good predictors will have more capital to bet with, and bad predictors will have less capital to bet with. This does not rely on anyone "getting wiser" or "learning their lesson" or any other assumption about humans' capacity to reason and learn. It is simply a result of selection dynamics that over time, participants that are good at making correct guesses will come to dominate the ecosystem.Note that prediction markets fare better than stock markets in this regard: the "nouveau riche" of stock markets often arise from getting lucky on a single thousandfold gain, adding a lot of noise to the signal, but in prediction markets, prices are bounded between 0 and 1, limiting the impact of any one single event.Better participants and better technologySecond, prediction markets themselves will improve. User interfaces have greatly improved already, and will continue to improve further. The complexity of the MakerDAO -> Foundry -> Catnip cycle will be abstracted away into a single transaction. Blockchain scaling technology will improve, reducing fees for participants (The ZK-rollup Loopring with a built-in AMM is already live on the Ethereum mainnet, and a prediction market could theoretically run on it).Third, the demonstration that we saw of the prediction market working correctly will ease participants' fears. Users will see that the Augur oracle is capable of giving correct outputs even in very contentious situations (this time, there were two rounds of disputes, but the no side nevertheless cleanly won). People from outside the crypto space will see that the process works and be more inclined to participate. Perhaps even Nate Silver himself might get some DAI and use Augur, Omen, Polymarket and other markets to supplement his income in 2022 and beyond.Fourth, prediction market tech itself could improve. Here is a proposal from myself on a market design that could make it more capital-efficient to simultaneously bet against many unlikely events, helping to prevent unlikely outcomes from getting irrationally high odds. Other ideas will surely spring up, and I look forward to seeing more experimentation in this direction.ConclusionThis whole saga has proven to be an incredibly interesting direct trial-by-first test of prediction markets and how they collide with the complexities of individual and social psychology. It shows a lot about how market efficiency actually works in practice, what are the limits of it and what could be done to improve it.It has also been an excellent demonstration of the power of blockchains; in fact, it is one of the Ethereum applications that have provided to me the most concrete value. Blockchains are often criticized for being speculative toys and not doing anything meaningful except for self-referential games (tokens, with yield farming, whose returns are powered by... the launch of other tokens). There are certainly exceptions that the critics fail to recognize; I personally have benefited from ENS and even from using ETH for payments on several occasions where all credit card options failed. But over the last few months, it seems like we have seen a rapid burst in Ethereum applications being concretely useful for people and interacting with the real world, and prediction markets are a key example of this.I expect prediction markets to become an increasingly important Ethereum application in the years to come. The 2020 election was only the beginning; I expect more interest in prediction markets going forward, not just for elections but for conditional predictions, decision-making and other applications as well. The amazing promises of what prediction markets could bring if they work mathematically optimally will, of course, continue to collide with the limits of human reality, and hopefully, over time, we will get a much clearer view of exactly where this new social technology can provide the most value.

Endnotes on 2020: Crypto and Beyond Endnotes on 2020: Crypto and Beyond2020 Dec 28 See all posts Endnotes on 2020: Crypto and Beyond I'm writing this sitting in Singapore, the city in which I've now spent nearly half a year of uninterrupted time - an unremarkable duration for many, but for myself the longest I've stayed in any one place for nearly a decade. After months of fighting what may perhaps even be humanity's first boss-level enemy since 1945, the city itself is close to normal, though the world as a whole and its 7.8 billion inhabitants, normally so close by, continue to be so far away. Many other parts of the world have done less well and suffered more, though there is now a light at the end of the tunnel, as hopefully rapid deployment of vaccines will help humanity as a whole overcome this great challenge.2020 has been a strange year because of these events, but also others. As life "away from keyboard (AFK)" has gotten much more constrained and challenging, the internet has been supercharged, with consequences both good and bad. Politics around the world has gone in strange directions, and I am continually worried by the many political factions that are so easily abandoning their most basic principles because they seem to have decided that their (often mutually contradictory) personal causes are just too important. And yet at the same time, there are rays of hope coming from unusual corners, with new technological discoveries in transportation, medicine, artificial intelligence - and, of course, blockchains and cryptography - that could open up a new chapter for humanity finally coming to fruition. Where we started Where we're going And so, 2020 is as good a year as any to ponder a key question: how should we re-evaluate our models of the world? What ways of seeing, understanding and reasoning about the world are going to be more useful in the decades to come, and what paths are no longer as valuable? What paths did we not see before that were valuable all along? In this post, I will give some of my own answers, covering far from everything but digging into a few specifics that seem particularly interesting. It's sometimes hard to tell which of these ideas are a recognition of a changing reality, and which are just myself finally seeing what has always been there; often enough it's some of both. The answers to these questions have a deep relevance both to the crypto space that I call home as well as to the wider world.The Changing Role of EconomicsEconomics has historically focused on "goods" in the form of physical objects: production of food, manufacturing of widgets, buying and selling houses, and the like. Physical objects have some particular properties: they can be transferred, destroyed, bought and sold, but not copied. If one person is using a physical object, it's usually impractical for another person to use it simultaneously. Many objects are only valuable if "consumed" outright. Making ten copies of an object requires something close to ten times the resources that it takes to make one (not quite ten times, but surprisingly close, especially at larger scales). But on the internet, very different rules apply. Copying is cheap. I can write an article or a piece of code once, and it usually takes quite a bit of effort to write it once, but once that work is done, an unlimited number of people can download and enjoy it. Very few things are "consumable"; often products are superseded by better ones, but if that does not happen, something produced today may continue to provide value to people until the end of time.On the internet, "public goods" take center stage. Certainly, private goods exist, particularly in the form of individuals' scarce attention and time and virtual assets that command that attention, but the average interaction is one-to-many, not one-to-one. Confounding the situation even further, the "many" rarely maps easily to our traditional structures for structuring one-to-many interactions, such as companies, cities or countries;. Instead, these public goods are typically public across a widely scattered collection of people all around the world. Many online platforms serving wide groups of people need governance, to decide on features, content moderation policies or other challenges important to their user community, though there too, the user community rarely maps cleanly to anything but itself. How is it fair for the US government to govern Twitter, when Twitter is often a platform for public debates between US politicians and representatives of its geopolitical rivals? But clearly, governance challenges exist - and so we need more creative solutions.This is not merely of interest to "pure" online services. Though goods in the physical world - food, houses, healthcare, transportation - continue to be as important as ever, improvements in these goods depend even more than before on technology, and technological progress does happen over the internet. Examples of important public goods in the Ethereum ecosystem that were funded by the recent Gitcoin quadratic funding round. Open source software ecosystems, including blockchains, are hugely dependent on public goods.But also, economics itself seems to be a less powerful tool in dealing with these issues. Out of all the challenges of 2020, how many can be understood by looking at supply and demand curves? One way to see what is going on here is by looking at the relationship between economics and politics. In the 19th century, the two were frequently viewed as being tied together, a subject called "political economy". In the 20th century, the two are more typically split apart. But in the 21st century, the lines between "private" and "public" are once again rapidly blurring. Governments are behaving more like market actors, and corporations are behaving more like governments.We see this merge happening in the crypto space as well, as the researchers' eye of attention is increasingly switching focus to the challenge of governance. Five years ago, the main economic topics being considered in the crypto space had to do with consensus theory. This is a tractable economics problem with clear goals, and so we would on several occasions obtain nice clean results like the selfish mining paper. Some points of subjectivity, like quantifying decentralization, exist, but they could be easily encapsulated and treated separately from the formal math of the mechanism design. But in the last few years, we have seen the rise of increasingly complicated financial protocols and DAOs on top of blockchains, and at the same time governance challenges within blockchains. Should Bitcoin Cash redirect 12.5% of its block reward toward paying a developer team? If so, who decides who that developer team is? Should Zcash extend its 20% developer reward for another four years? These problems certainly can be analyzed economically to some extent, but the analysis inevitably gets stuck at concepts like coordination, flipping between equilibria, "Schelling points" and "legitimacy", that are much more difficult to express with numbers. And so, a hybrid discipline, combining formal mathematical reasoning with the softer style of humanistic reasoning, is required.We wanted digital nations, instead we got digital nationalismOne of the most fascinating things that I noticed fairly early in the crypto space starting from around 2014 is just how quickly it started replicating the political patterns of the world at large. I don't mean this just in some broad abstract sense of "people are forming tribes and attacking each other", I mean similarities that are surprisingly deep and specific.First, the story. From 2009 to about 2013, the Bitcoin world was a relatively innocent happy place. The community was rapidly growing, prices were rising, and disagreements over block size or long-term direction, while present, were largely academic and took up little attention compared to the shared broader goal of helping Bitcoin grow and prosper.But in 2014, the schisms started to arise. Transaction volumes on the Bitcoin blockchain hit 250 kilobytes per block and kept rising, for the first time raising fears that blockchain usage might actually hit the 1 MB limit before the limit could be increased. Non-Bitcoin blockchains, up until this point a minor sideshow, suddenly became a major part of the space, with Ethereum itself arguably leading the charge. And it was during these events that disagreements that were before politely hidden beneath the surface suddenly blew up. "Bitcoin maximalism", the idea that the goal of the crypto space should not be a diverse ecosystem of cryptocurrencies generally but Bitcoin and Bitcoin alone specifically, grew from a niche curiosity into a prominent and angry movement that Dominic Williams and I quickly saw for what it is and gave its current name. The small block ideology, arguing that the block size should be increased very slowly or even never increased at all regardless of how high transaction fees go, began to take root.The disagreements within Bitcoin would soon turn into an all-out civil war. Theymos, the operator of the /r/bitcoin subreddit and several other key public Bitcoin discussion spaces, resorted to extreme censorship to impose his (small-block-leaning) views on the community. In response, the big-blockers moved to a new subreddit, /r/btc. Some valiantly attempted to defuse tensions with diplomatic conferences including a famous one in Hong Kong, and a seeming consensus was reached, though one year later the small block side would end up reneging on its part of the deal. By 2017, the big block faction was firmly on its way to defeat, and in August of that year they would secede (or "fork off") to implement their own vision on their own separate continuation of the Bitcoin blockchain, which they called "Bitcoin Cash" (symbol BCH).The community split was chaotic, and one can see this in how the channels of communication were split up in the divorce: /r/bitcoin stayed under the control of supporters of Bitcoin (BTC). /r/btc was controlled by supporters of Bitcoin Cash (BCH). Bitcoin.org was controlled by supporters of Bitcoin (BTC). Bitcoin.com on the other hand was controlled by supporters of Bitcoin Cash (BCH). Each side claimed themselves to be the true Bitcoin. The result looked remarkably similar to one of those civil wars that happens from time to time that results in a country splitting in half, the two halves calling themselves almost identical names that differ only in which subset of the words "democratic", "people's" and "republic" appears on each side. Neither side had the ability to destroy the other, and of course there was no higher authority to adjudicate the dispute. Major Bitcoin forks, as of 2020. Does not include Bitcoin Diamond, Bitcoin Rhodium, Bitcoin Private, or any of the other long list of Bitcoin forks that I would highly recommend you just ignore completely, except to sell (and perhaps you should sell some of the forks listed above too, eg. BSV is definitely a scam!)Around the same time, Ethereum had its own chaotic split, in the form of the DAO fork, a highly controversial resolution to a theft in which over $50 million was stolen from the first major smart contract application on Ethereum. Just like in the Bitcoin case, there was first a civil war - though only lasting four weeks - and then a chain split, followed by an online war between the two now-separate chains, Ethereum (ETH) and Ethereum Classic (ETC). The naming split was as fun as in Bitcoin: the Ethereum Foundation held ethereumproject on Twitter but Ethereum Classic supporters held ethereumproject on Github.Some on the Ethereum side would argue that Ethereum Classic had very few "real" supporters, and the whole thing was mostly a social attack by Bitcoin supporters: either to support the version of Ethereum that aligned with their values, or to cause chaos and destroy Ethereum outright. I myself believed these claims somewhat at the beginning, though over time I came to realize that they were overhyped. It is true that some Bitcoin supporters had certainly tried to shape the outcome in their own image. But to a large extent, as is the case in many conflicts, the "foreign interference" card was simply a psychological defense that many Ethereum supporters, myself included, subconsciously used to shield ourselves from the fact that many people within our own community really did have different values. Fortunately relations between the two currencies have since improved - in part thanks to the excellent diplomatic skills of Virgil Griffith - and Ethereum Classic developers have even agreed to move to a different Github page.Civil wars, alliances, blocs, alliances with participants in civil wars, you can all find it in crypto. Though fortunately, the conflict is all virtual and online, without the extremely harmful in-person consequences that often come with such things happening in real life. So what can we learn from all this? One important takeaway is this: if phenomena like this happen in contexts as widely different from each other as conflicts between countries, conflicts between religions and relations within and between purely digital cryptocurrencies, then perhaps what we're looking at is the indelible epiphenomena of human nature - something much more difficult to resolve than by changing what kinds of groups we organize in. So we should expect situations like this to continue to play out in many contexts over the decades to come. And perhaps it's harder than we thought to separate the good that may come out of this from the bad: those same energies that drive us to fight also drive us to contribute.What motivates us anyway?One of the key intellectual undercurrents of the 2000s era was the recognition of the importance of non-monetary motivations. People are motivated not just by earning as much money as possible in the work and extracting enjoyment from their money in their family lives; even at work we are motivated by social status, honor, altruism, reciprocity, a feeling of contribution, different social conceptions of what is good and valuable, and much more.These differences are very meaningful and measurable. For one example, see this Swiss study on compensating differentials for immoral work - how much extra do employers have to pay to convince someone to do a job if that job is considered morally unsavory?As we can see, the effects are massive: if a job is widely considered immoral, you need to pay employees almost twice as much for them to be willing to do it. From personal experience, I would even argue that this understates the case: in many cases, top-quality workers would not be willing to work for a company that they think is bad for the world at almost any price. "Work" that is difficult to formalize (eg. word-of-mouth marketing) functions similarly: if people think a project is good, they will do it for free, if they do not, they will not do it at all. This is also likely why blockchain projects that raise a lot of money but are unscrupulous, or even just corporate-controlled profit-oriented "VC chains", tend to fail: even a billion dollars of capital cannot compete with a project having a soul.That said, it is possible to be overly idealistic about this fact, in several ways. First of all, while this decentralized, non-market, non-governmental subsidy toward projects that are socially considered to be good is massive, likely amounting to tens of trillions of dollars per year globally, its effect is not infinite. If a developer has a choice between earning $30,000 per year by being "ideologically pure", and making a $30 million ICO by sticking a needless token into their project, they will do the latter. Second, idealistic motivations are uneven in what they motivate. Rick Falkvinge's Swarmwise played up the possibility of decentralized non-market organization in part by pointing to political activism as a key example. And this is true, political activism does not require getting paid. But longer and more grueling tasks, even something as simple as making good user interfaces, are not so easily intrinsically motivated. And so if you rely on intrinsic motivation too much, you get projects where some tasks are overdone and other tasks are done poorly, or even ignored entirely. And third, perceptions of what people find intrinsically attractive to work on may change, and may even be manipulated.One important conclusion for me from this is the importance of culture (and that oh-so-important word that crypto influencers have unfortunately ruined for me, "narrative"). If a project having a high moral standing is equivalent to that project having twice as much money, or even more, then culture and narrative are extremely powerful forces that command the equivalent of tens of trillions of dollars of value. And this does not even begin to cover the role of such concepts in shaping our perceptions of legitimacy and coordination. And so anything that influences the culture can have a great impact on the world and on people's financial interests, and we're going to see more and more sophisticated efforts from all kinds of actors to do so systematically and deliberately. This is the darker conclusion of the importance of non-monetary social motivations - they create the battlefield for the permanent and final frontier of war, the war that is fortunately not usually deadly but unfortunately impossible to create peace treaties for because of how inextricably subjective it is to determine what even counts as a battle: the culture war.Big X is here to stay, for all XOne of the great debates of the 20th century is that between "Big Government" and "Big Business" - with various permutations of each: Big Brother, Big Banks, Big Tech, also at times joining the stage. In this environment, the Great Ideologies were typically defined by trying to abolish the Big X that they disliked: communism focusing on corporations, anarcho-capitalism on governments, and so forth. Looking back in 2020, one may ask: which of the Great Ideologies succeeded, and which failed?Let us zoom into one specific example: the 1996 Declaration of Independence of Cyberspace:Governments of the Industrial World, you weary giants of flesh and steel, I come from Cyberspace, the new home of Mind. On behalf of the future, I ask you of the past to leave us alone. You are not welcome among us. You have no sovereignty where we gather.And the similarly-spirited Crypto-Anarchist Manifesto:Computer technology is on the verge of providing the ability for individuals and groups to communicate and interact with each other in a totally anonymous manner. Two persons may exchange messages, conduct business, and negotiate electronic contracts without ever knowing the True Name, or legal identity, of the other. Interactions over networks will be untraceable, via extensive re-routing of encrypted packets and tamper-proof boxes which implement cryptographic protocols with nearly perfect assurance against any tampering. Reputations will be of central importance, far more important in dealings than even the credit ratings of today. These developments will alter completely the nature of government regulation, the ability to tax and control economic interactions, the ability to keep information secret, and will even alter the nature of trust and reputation.How have these predictions fared? The answer is interesting: I would say that they succeeded in one part and failed in the other. What succeeded? We have interactions over networks, we have powerful cryptography that is difficult for even state actors to break, we even have powerful cryptocurrency, with smart contract capabilities that the thinkers of the 1990s mostly did not even anticipate, and we're increasingly moving toward anonymized reputation systems with zero knowledge proofs. What failed? Well, the government did not go away. And what just proved to be totally unexpected? Perhaps the most interesting plot twist is that the two forces are, a few exceptions notwithstanding, by and large not acting like mortal enemies, and there are even many people within governments that are earnestly trying to find ways to be friendly to blockchains and cryptocurrency and new forms of cryptographic trust.What we see in 2020 is this: Big Government is as powerful as ever, but Big Business is also as powerful as ever. "Big Protest Mob" is as powerful as ever too, as is Big Tech, and soon enough perhaps Big Cryptography. It's a densely populated jungle, with an uneasy peace between many complicated actors. If you define success as the total absence of a category of powerful actor or even a category of activity that you dislike, then you will probably leave the 21st century disappointed. But if you define success more through what happens than through what doesn't happen, and you are okay with imperfect outcomes, there is enough space to make everyone happy. Often, the boundary between multiple intersecting worlds is the most interesting place to be. The monkeys get it.Prospering in the dense jungleSo we have a world where:One-to-one interactions are less important, one-to-many and many-to-many interactions are more important. The environment is much more chaotic, and difficult to model with clean and simple equations. Many-to-many interactions particularly follow strange rules that we still do not understand well. The environment is dense, and different categories of powerful actors are forced to live quite closely side by side with each other. In some ways, this is a world that is less convenient for someone like myself. I grew up with a form of economics that is focused on analyzing simpler physical objects and buying and selling, and am now forced to contend with a world where such analysis, while not irrelevant, is significantly less relevant than before. That said, transitions are always challenging. In fact, transitions are particularly challenging for those who think that they are not challenging because they think that the transition merely confirms what they believed all along. If you are still operating today precisely according to a script that was created in 2009, when the Great Financial Crisis was the most recent pivotal event on anyone's mind, then there are almost certainly important things that happened in the last decade that you are missing. An ideology that's finished is an ideology that's dead.It's a world where blockchains and cryptocurrencies are well poised to play an important part, though for reasons much more complex than many people think, and having as much to do with cultural forces as anything financial (one of the more underrated bull cases for cryptocurrency that I have always believed is simply the fact that gold is lame, the younger generations realize that it's lame, and that $9 trillion has to go somewhere). Similarly complex forces are what will lead to blockchains and cryptocurrencies being useful. It's easy to say that any application can be done more efficiently with a centralized service, but in practice social coordination problems are very real, and unwillingness to sign onto a system that has even a perception of non-neutrality or ongoing dependence on a third party is real too. And so the centralized and even consortium-based approaches claiming to replace blockchains don't get anywhere, while "dumb and inefficient" public-blockchain-based solutions just keep quietly moving forward and gaining actual adoption.And finally it's a very multidisciplinary world, one that is much harder to break up into layers and analyze each layer separately. You may need to switch from one style of analysis to another style of analysis in mid-sentence. Things happen for strange and inscrutable reasons, and there are always surprises. The question that remains is: how do we adapt to it?

An Incomplete Guide to Rollups An Incomplete Guide to Rollups2021 Jan 05 See all posts An Incomplete Guide to Rollups Rollups are all the rage in the Ethereum community, and are poised to be the key scalability solution for Ethereum for the foreseeable future. But what exactly is this technology, what can you expect from it and how will you be able to use it? This post will attempt to answer some of those key questions.Background: what is layer-1 and layer-2 scaling?There are two ways to scale a blockchain ecosystem. First, you can make the blockchain itself have a higher transaction capacity. The main challenge with this technique is that blockchains with "bigger blocks" are inherently more difficult to verify and likely to become more centralized. To avoid such risks, developers can either increase the efficiency of client software or, more sustainably, use techniques such as sharding to allow the work of building and verifying the chain to be split up across many nodes; the effort known as "eth2" is currently building this upgrade to Ethereum.Second, you can change the way that you use the blockchain. Instead of putting all activity on the blockchain directly, users perform the bulk of their activity off-chain in a "layer 2" protocol. There is a smart contract on-chain, which only has two tasks: processing deposits and withdrawals, and verifying proofs that everything happening off-chain is following the rules. There are multiple ways to do these proofs, but they all share the property that verifying the proofs on-chain is much cheaper than doing the original computation off-chain.State channels vs plasma vs rollupsThe three major types of layer-2 scaling are state channels, Plasma and rollups. They are three different paradigms, with different strengths and weaknesses, and at this point we are fairly confident that all layer-2 scaling falls into roughly these three categories (though naming controversies exist at the edges, eg. see "validium").How do channels work?See also: https://www.jeffcoleman.ca/state-channels and statechannels.orgImagine that Alice is offering an internet connection to Bob, in exchange for Bob paying her $0.001 per megabyte. Instead of making a transaction for each payment, Alice and Bob use the following layer-2 scheme.First, Bob puts $1 (or some ETH or stablecoin equivalent) into a smart contract. To make his first payment to Alice, Bob signs a "ticket" (an off-chain message), that simply says "$0.001", and sends it to Alice. To make his second payment, Bob would sign another ticket that says "$0.002", and send it to Alice. And so on and so forth for as many payments as needed. When Alice and Bob are done transacting, Alice can publish the highest-value ticket to chain, wrapped in another signature from herself. The smart contract verifies Alice and Bob's signatures, pays Alice the amount on Bob's ticket and returns the rest to Bob. If Alice is unwilling to close the channel (due to malice or technical failure), Bob can initiate a withdrawal period (eg. 7 days); if Alice does not provide a ticket within that time, then Bob gets all his money back.This technique is powerful: it can be adjusted to handle bidirectional payments, smart contract relationships (eg. Alice and Bob making a financial contract inside the channel), and composition (if Alice and Bob have an open channel and so do Bob and Charlie, Alice can trustlessly interact with Charlie). But there are limits to what channels can do. Channels cannot be used to send funds off-chain to people who are not yet participants. Channels cannot be used to represent objects that do not have a clear logical owner (eg. Uniswap). And channels, especially if used to do things more complex than simple recurring payments, require a large amount of capital to be locked up.How does plasma work?See also: the original Plasma paper, and Plasma Cash.To deposit an asset, a user sends it to the smart contract managing the Plasma chain. The Plasma chain assigns that asset a new unique ID (eg. 537). Each Plasma chain has an operator (this could be a centralized actor, or a multisig, or something more complex like PoS or DPoS). Every interval (this could be 15 seconds, or an hour, or anything in between), the operator generates a "batch" consisting of all of the Plasma transactions they have received off-chain. They generate a Merkle tree, where at each index X in the tree, there is a transaction transferring asset ID X if such a transaction exists, and otherwise that leaf is zero. They publish the Merkle root of this tree to chain. They also send the Merkle branch of each index X to the current owner of that asset. To withdraw an asset, a user publishes the Merkle branch of the most recent transaction sending the asset to them. The contract starts a challenge period, during which anyone can try to use other Merkle branches to invalidate the exit by proving that either (i) the sender did not own the asset at the time they sent it, or (ii) they sent the asset to someone else at some later point in time. If no one proves that the exit is fraudulent for (eg.) 7 days, the user can withdraw the asset.Plasma provides stronger properties than channels: you can send assets to participants who were never part of the system, and the capital requirements are much lower. But it comes at a cost: channels require no data whatsoever to go on chain during "normal operation", but Plasma requires each chain to publish one hash at regular intervals. Additionally, Plasma transfers are not instant: you have to wait for the interval to end and for the block to be published.Additionally, Plasma and channels share a key weakness in common: the game theory behind why they are secure relies on the idea that each object controlled by both systems has some logical "owner". If that owner does not care about their asset, then an "invalid" outcome involving that asset may result. This is okay for many applications, but it is a deal breaker for many others (eg. Uniswap). Even systems where the state of an object can be changed without the owner's consent (eg. account-based systems, where you can increase someone's balance without their consent) do not work well with Plasma. This all means that a large amount of "application-specific reasoning" is required in any realistic plasma or channels deployment, and it is not possible to make a plasma or channel system that just simulates the full ethereum environment (or "the EVM"). To get around this problem, we get to... rollups.RollupsSee also: EthHub on optimistic rollups and ZK rollups.Plasma and channels are "full" layer 2 schemes, in that they try to move both data and computation off-chain. However, fundamental game theory issues around data availability means that it is impossible to safely do this for all applications. Plasma and channels get around this by relying on an explicit notion of owners, but this prevents them from being fully general. Rollups, on the other hand, are a "hybrid" layer 2 scheme. Rollups move computation (and state storage) off-chain, but keep some data per transaction on-chain. To improve efficiency, they use a whole host of fancy compression tricks to replace data with computation wherever possible. The result is a system where scalability is still limited by the data bandwidth of the underlying blockchain, but at a very favorable ratio: whereas an Ethereum base-layer ERC20 token transfer costs ~45000 gas, an ERC20 token transfer in a rollup takes up 16 bytes of on-chain space and costs under 300 gas.The fact that data is on-chain is key (note: putting data "on IPFS" does not work, because IPFS does not provide consensus on whether or not any given piece of data is available; the data must go on a blockchain). Putting data on-chain and having consensus on that fact allows anyone to locally process all the operations in the rollup if they wish to, allowing them to detect fraud, initiate withdrawals, or personally start producing transaction batches. The lack of data availability issues means that a malicious or offline operator can do even less harm (eg. they cannot cause a 1 week delay), opening up a much larger design space for who has the right to publish batches and making rollups vastly easier to reason about. And most importantly, the lack of data availability issues means that there is no longer any need to map assets to owners, leading to the key reason why the Ethereum community is so much more excited about rollups than previous forms of layer 2 scaling: rollups are fully general-purpose, and one can even run an EVM inside a rollup, allowing existing Ethereum applications to migrate to rollups with almost no need to write any new code.OK, so how exactly does a rollup work?There is a smart contract on-chain which maintains a state root: the Merkle root of the state of the rollup (meaning, the account balances, contract code, etc, that are "inside" the rollup). Anyone can publish a batch, a collection of transactions in a highly compressed form together with the previous state root and the new state root (the Merkle root after processing the transactions). The contract checks that the previous state root in the batch matches its current state root; if it does, it switches the state root to the new state root. To support depositing and withdrawing, we add the ability to have transactions whose input or output is "outside" the rollup state. If a batch has inputs from the outside, the transaction submitting the batch needs to also transfer these assets to the rollup contract. If a batch has outputs to the outside, then upon processing the batch the smart contract initiates those withdrawals.And that's it! Except for one major detail: how to do know that the post-state roots in the batches are correct? If someone can submit a batch with any post-state root with no consequences, they could just transfer all the coins inside the rollup to themselves. This question is key because there are two very different families of solutions to the problem, and these two families of solutions lead to the two flavors of rollups.Optimistic rollups vs ZK rollupsThe two types of rollups are:Optimistic rollups, which use fraud proofs: the rollup contract keeps track of its entire history of state roots and the hash of each batch. If anyone discovers that one batch had an incorrect post-state root, they can publish a proof to chain, proving that the batch was computed incorrectly. The contract verifies the proof, and reverts that batch and all batches after it. ZK rollups, which use validity proofs: every batch includes a cryptographic proof called a ZK-SNARK (eg. using the PLONK protocol), which proves that the post-state root is the correct result of executing the batch. No matter how large the computation, the proof can be very quickly verified on-chain. There are complex tradeoffs between the two flavors of rollups:Property Optimistic rollups ZK rollups Fixed gas cost per batch ~40,000 (a lightweight transaction that mainly just changes the value of the state root) ~500,000 (verification of a ZK-SNARK is quite computationally intensive) Withdrawal period ~1 week (withdrawals need to be delayed to give time for someone to publish a fraud proof and cancel the withdrawal if it is fraudulent) Very fast (just wait for the next batch) Complexity of technology Low High (ZK-SNARKs are very new and mathematically complex technology) Generalizability Easier (general-purpose EVM rollups are already close to mainnet) Harder (ZK-SNARK proving general-purpose EVM execution is much harder than proving simple computations, though there are efforts (eg. Cairo) working to improve on this) Per-transaction on-chain gas costs Higher Lower (if data in a transaction is only used to verify, and not to cause state changes, then this data can be left out, whereas in an optimistic rollup it would need to be published in case it needs to be checked in a fraud proof) Off-chain computation costs Lower (though there is more need for many full nodes to redo the computation) Higher (ZK-SNARK proving especially for general-purpose computation can be expensive, potentially many thousands of times more expensive than running the computation directly) In general, my own view is that in the short term, optimistic rollups are likely to win out for general-purpose EVM computation and ZK rollups are likely to win out for simple payments, exchange and other application-specific use cases, but in the medium to long term ZK rollups will win out in all use cases as ZK-SNARK technology improves.Anatomy of a fraud proofThe security of an optimistic rollup depends on the idea that if someone publishes an invalid batch into the rollup, anyone else who was keeping up with the chain and detected the fraud can publish a fraud proof, proving to the contract that that batch is invalid and should be reverted. A fraud proof claiming that a batch was invalid would contain the data in green: the batch itself (which could be checked against a hash stored on chain) and the parts of the Merkle tree needed to prove just the specific accounts that were read and/or modified by the batch. The nodes in the tree in yellow can be reconstructed from the nodes in green and so do not need to be provided. This data is sufficient to execute the batch and compute the post-state root (note that this is exactly the same as how stateless clients verify individual blocks). If the computed post-state root and the provided post-state root in the batch are not the same, then the batch is fraudulent.It is guaranteed that if a batch was constructed incorrectly, and all previous batches were constructed correctly, then it is possible to create a fraud proof showing the the batch was constructed incorrectly. Note the claim about previous batches: if there was more than one invalid batch published to the rollup, then it is best to try to prove the earliest one invalid. It is also, of course, guaranteed that if a batch was constructed correctly, then it is never possible to create a fraud proof showing that the batch is invalid.How does compression work?A simple Ethereum transaction (to send ETH) takes ~110 bytes. An ETH transfer on a rollup, however, takes only ~12 bytes:Parameter Ethereum Rollup Nonce ~3 0 Gasprice ~8 0-0.5 Gas 3 0-0.5 To 21 4 Value ~9 ~3 Signature ~68 (2 + 33 + 33) ~0.5 From 0 (recovered from sig) 4 Total ~112 ~12 Part of this is simply superior encoding: Ethereum's RLP wastes 1 byte per value on the length of each value. But there are also some very clever compression tricks that are going on:Nonce: the purpose of this parameter is to prevent replays. If the current nonce of an account is 5, the next transaction from that account must have nonce 5, but once the transaction is processed the nonce in the account will be incremented to 6 so the transaction cannot be processed again. In the rollup, we can omit the nonce entirely, because we just recover the nonce from the pre-state; if someone tries replaying a transaction with an earlier nonce, the signature would fail to verify, as the signature would be checked against data that contains the new higher nonce. Gasprice: we can allow users to pay with a fixed range of gasprices, eg. a choice of 16 consecutive powers of two. Alternatively, we could just have a fixed fee level in each batch, or even move gas payment outside the rollup protocol entirely and have transactors pay batch creators for inclusion through a channel. Gas: we could similarly restrict the total gas to a choice of consecutive powers of two. Alternatively, we could just have a gas limit only at the batch level. To: we can replace the 20-byte address with an index (eg. if an address is the 4527th address added to the tree, we just use the index 4527 to refer to it. We would add a subtree to the state to store the mapping of indices to addresses). Value: we can store value in scientific notation. In most cases, transfers only need 1-3 significant digits. Signature: we can use BLS aggregate signatures, which allows many signatures to be aggregated into a single ~32-96 byte (depending on protocol) signature. This signature can then be checked against the entire set of messages and senders in a batch all at once. The ~0.5 in the table represents the fact that there is a limit on how many signatures can be combined in an aggregate that can be verified in a single block, and so large batches would need one signature per ~100 transactions. One important compression trick that is specific to ZK rollups is that if a part of a transaction is only used for verification, and is not relevant to computing the state update, then that part can be left off-chain. This cannot be done in an optimistic rollup because that data would still need to be included on-chain in case it needs to be later checked in a fraud proof, whereas in a ZK rollup the SNARK proving correctness of the batch already proves that any data needed for verification was provided. An important example of this is privacy-preserving rollups: in an optimistic rollup the ~500 byte ZK-SNARK used for privacy in each transaction needs to go on chain, whereas in a ZK rollup the ZK-SNARK covering the entire batch already leaves no doubt that the "inner" ZK-SNARKs are valid.These compression tricks are key to the scalability of rollups; without them, rollups would be perhaps only a ~10x improvement on the scalability of the base chain (though there are some specific computation-heavy applications where even simple rollups are powerful), whereas with compression tricks the scaling factor can go over 100x for almost all applications.Who can submit a batch?There are a number of schools of thought for who can submit a batch in an optimistic or ZK rollup. Generally, everyone agrees that in order to be able to submit a batch, a user must put down a large deposit; if that user ever submits a fraudulent batch (eg. with an invalid state root), that deposit would be part burned and part given as a reward to the fraud prover. But beyond that, there are many possibilities:Total anarchy: anyone can submit a batch at any time. This is the simplest approach, but it has some important drawbacks. Particularly, there is a risk that multiple participants will generate and attempt to submit batches in parallel, and only one of those batches can be successfully included. This leads to a large amount of wasted effort in generating proofs and/or wasted gas in publishing batches to chain. Centralized sequencer: there is a single actor, the sequencer, who can submit batches (with an exception for withdrawals: the usual technique is that a user can first submit a withdrawal request, and then if the sequencer does not process that withdrawal in the next batch, then the user can submit a single-operation batch themselves). This is the most "efficient", but it is reliant on a central actor for liveness. Sequencer auction: an auction is held (eg. every day) to determine who has the right to be the sequencer for the next day. This technique has the advantage that it raises funds which could be distributed by eg. a DAO controlled by the rollup (see: MEV auctions) Random selection from PoS set: anyone can deposit ETH (or perhaps the rollup's own protocol token) into the rollup contract, and the sequencer of each batch is randomly selected from one of the depositors, with the probability of being selected being proportional to the amount deposited. The main drawback of this technique is that it leads to large amounts of needless capital lockup. DPoS voting: there is a single sequencer selected with an auction but if they perform poorly token holders can vote to kick them out and hold a new auction to replace them. Split batching and state root provisionSome of the rollups being currently developed are using a "split batch" paradigm, where the action of submitting a batch of layer-2 transactions and the action of submitting a state root are done separately. This has some key advantages:You can allow many sequencers in parallel to publish batches in order to improve censorship resistance, without worrying that some batches will be invalid because some other batch got included first. If a state root is fraudulent, you don't need to revert the entire batch; you can revert just the state root, and wait for someone to provide a new state root for the same batch. This gives transaction senders a better guarantee that their transactions will not be reverted. So all in all, there is a fairly complex zoo of techniques that are trying to balance between complicated tradeoffs involving efficiency, simplicity, censorship resistance and other goals. It's still too early to say which combination of these ideas works best; time will tell.How much scaling do rollups give you?On the existing Ethereum chain, the gas limit is 12.5 million, and each byte of data in a transaction costs 16 gas. This means that if a block contains nothing but a single batch (we'll say a ZK rollup is used, spending 500k gas on proof verification), that batch can have (12 million / 16) = 750,000 bytes of data. As shown above, a rollup for ETH transfers requires only 12 bytes per user operation, meaning that the batch can contain up to 62,500 transactions. At an average block time of 13 seconds, this translates to ~4807 TPS (compared to 12.5 million / 21000 / 13 ~= 45 TPS for ETH transfers directly on Ethereum itself).Here's a chart for some other example use cases:Application Bytes in rollup Gas cost on layer 1 Max scalability gain ETH transfer 12 21,000 105x ERC20 transfer 16 (4 more bytes to specify which token) ~50,000 187x Uniswap trade ~14 (4 bytes sender + 4 bytes recipient + 3 bytes value + 1 byte max price + 1 byte misc) ~100,000 428x Privacy-preserving withdrawal (Optimistic rollup) 296 (4 bytes index of root + 32 bytes nullifier + 4 bytes recipient + 256 bytes ZK-SNARK proof) ~380,000 77x Privacy-preserving withdrawal (ZK rollup) 40 (4 bytes index of root + 32 bytes nullifier + 4 bytes recipient) ~380,000 570x Max scalability gain is calculated as (L1 gas cost) / (bytes in rollup * 16) * 12 million / 12.5 million.Now, it is worth keeping in mind that these figures are overly optimistic for a few reasons. Most importantly, a block would almost never just contain one batch, at the very least because there are and will be multiple rollups. Second, deposits and withdrawals will continue to exist. Third, in the short term usage will be low, and so fixed costs will dominate. But even with these factors taken into account, scalability gains of over 100x are expected to be the norm.Now what if we want to go above ~1000-4000 TPS (depending on the specific use case)? Here is where eth2 data sharding comes in. The sharding proposal opens up a space of 16 MB every 12 seconds that can be filled with any data, and the system guarantees consensus on the availability of that data. This data space can be used by rollups. This ~1398k bytes per sec is a 23x improvement on the ~60 kB/sec of the existing Ethereum chain, and in the longer term the data capacity is expected to grow even further. Hence, rollups that use eth2 sharded data can collectively process as much as ~100k TPS, and even more in the future.What are some not-yet-fully-solved challenges in rollups?While the basic concept of a rollup is now well-understood, we are quite certain that they are fundamentally feasible and secure, and multiple rollups have already been deployed to mainnet, there are still many areas of rollup design that have not been well explored, and quite a few challenges in fully bringing large parts of the Ethereum ecosystem onto rollups to take advantage of their scalability. Some key challenges include:User and ecosystem onboarding - not many applications use rollups, rollups are unfamiliar to users, and few wallets have started integrating rollups. Merchants and charities do not yet accept them for payments. Cross-rollup transactions - efficiently moving assets and data (eg. oracle outputs) from one rollup into another without incurring the expense of going through the base layer. Auditing incentives - how to maximize the chance that at least one honest node actually will be fully verifying an optimistic rollup so they can publish a fraud proof if something goes wrong? For small-scale rollups (up to a few hundred TPS) this is not a significant issue and one can simply rely on altruism, but for larger-scale rollups more explicit reasoning about this is needed. Exploring the design space in between plasma and rollups - are there techniques that put some state-update-relevant data on chain but not all of it, and is there anything useful that could come out of that? Maximizing security of pre-confirmations - many rollups provide a notion of "pre-confirmation" for faster UX, where the sequencer immediately provides a promise that a transaction will be included in the next batch, and the sequencer's deposit is destroyed if they break their word. But the economy security of this scheme is limited, because of the possibility of making many promises to very many actors at the same time. Can this mechanism be improved? Improving speed of response to absent sequencers - if the sequencer of a rollup suddenly goes offline, it would be valuable to recover from that situation maximally quickly and cheaply, either quickly and cheaply mass-exiting to a different rollup or replacing the sequencer. Efficient ZK-VM - generating a ZK-SNARK proof that general-purpose EVM code (or some different VM that existing smart contracts can be compiled to) has been executed correctly and has a given result. ConclusionsRollups are a powerful new layer-2 scaling paradigm, and are expected to be a cornerstone of Ethereum scaling in the short and medium-term future (and possibly long-term as well). They have seen a large amount of excitement from the Ethereum community because unlike previous attempts at layer-2 scaling, they can support general-purpose EVM code, allowing existing applications to easily migrate over. They do this by making a key compromise: not trying to go fully off-chain, but instead leaving a small amount of data per transaction on-chain.There are many kinds of rollups, and many choices in the design space: one can have an optimistic rollup using fraud proofs, or a ZK rollup using validity proofs (aka. ZK-SNARKs). The sequencer (the user that can publish transaction batches to chain) can be either a centralized actor, or a free-for-all, or many other choices in between. Rollups are still an early-stage technology, and development is continuing rapidly, but they work and some (notably Loopring, ZKSync and DeversiFi) have already been running for months. Expect much more exciting work to come out of the rollup space in the years to come.

Why Proof of Stake (Nov 2020) Why Proof of Stake (Nov 2020)2020 Nov 06 See all posts Why Proof of Stake (Nov 2020) There are three key reasons why PoS is a superior blockchain security mechanism compared to PoW.PoS offers more security for the same costThe easiest way to see this is to put proof of stake and proof of work side by side, and look at how much it costs to attack a network per $1 per day in block rewards.GPU-based proof of workYou can rent GPUs cheaply, so the cost of attacking the network is simply the cost of renting enough GPU power to outrun the existing miners. For every $1 of block rewards, the existing miners should be spending close to $1 in costs (if they're spending more, miners will drop out due to being unprofitable, if they're spending less, new miners can join in and take high profits). Hence, attacking the network just requires temporarily spending more than $1 per day, and only for a few hours.Total cost of attack: ~$0.26 (assuming 6-hour attack), potentially reduced to zero as the attacker receives block rewardsASIC-based proof of workASICs are a capital cost: you buy an ASIC once and you can expect it to be useful for ~2 years before it wears out and/or is obsoleted by newer and better hardware. If a chain gets 51% attacked, the community will likely respond by changing the PoW algorithm and your ASIC will lose its value. On average, mining is ~1/3 ongoing costs and ~2/3 capital costs (see here for some sources). Hence, per $1 per day in reward, miners will be spending ~$0.33 per day on electricity+maintenance and ~$0.67 per day on their ASIC. Assuming an ASIC lasts ~2 years, that's $486.67 that a miner would need to spend on that quantity of ASIC hardware.Total cost of attack: $486.67 (ASICs) + $0.08 (electricity+maintenance) = $486.75That said, it's worth noting that ASICs provide this heightened level of security against attacks at a high cost of centralization, as the barriers to entry to joining become very high.Proof of stakeProof of stake is almost entirely capital costs (the coins being deposited); the only operating costs are the cost of running a node. Now, how much capital are people willing to lock up to get $1 per day of rewards? Unlike ASICs, deposited coins do not depreciate, and when you're done staking you get your coins back after a short delay. Hence, participants should be willing to pay much higher capital costs for the same quantity of rewards.Let's assume that a ~15% rate of return is enough to motivate people to stake (that is the expected eth2 rate of return). Then, $1 per day of rewards will attract 6.667 years' worth of returns in deposits, or $2433. Hardware and electricity costs of a node are small; a thousand-dollar computer can stake for hundreds of thousands of dollars in deposits, and ~$100 per months in electricity and internet is sufficient for such an amount. But conservatively, we can say these ongoing costs are ~10% of the total cost of staking, so we only have $0.90 per day of rewards that end up corresponding to capital costs, so we do need to cut the above figure by ~10%.Total cost of attack: $0.90/day * 6.667 years = $2189In the long run, this cost is expected to go even higher, as staking becomes more efficient and people become comfortable with lower rates of return. I personally expect this number to eventually rise to something like $10000.Note that the only "cost" being incurred to get this high level of security is just the inconvenience of not being able to move your coins around at will while you are staking. It may even be the case that the public knowledge that all these coins are locked up causes the value of the coin to rise, so the total amount of money floating around in the community, ready to make productive investments etc, remains the same! Whereas in PoW, the "cost" of maintaining consensus is real electricity being burned in insanely large quantities.Higher security or lower costs?Note that there are two ways to use this 5-20x gain in security-per-cost. One is to keep block rewards the same but benefit from increased security. The other is to massively reduce block rewards (and hence the "waste" of the consensus mechanism) and keep the security level the same.Either way is okay. I personally prefer the latter, because as we will see below, in proof of stake even a successful attack is much less harmful and much easier to recover from than an attack on proof of work!Attacks are much easier to recover from in proof of stakeIn a proof of work system, if your chain gets 51% attacked, what do you even do? So far, the only response in practice has been "wait it out until the attacker gets bored". But this misses the possibility of a much more dangerous kind of attack called a spawn camping attack, where the attacker attacks the chain over and over again with the explicit goal of rendering it useless.In a GPU-based system, there is no defense, and a persistent attacker may quite easily render a chain permanently useless (or more realistically, switches to proof of stake or proof of authority). In fact, after the first few days, the attacker's costs may become very low, as honest miners will drop out since they have no way to get rewards while the attack is going on.In an ASIC-based system, the community can respond to the first attack, but continuing the attack from there once again becomes trivial. The community would meet the first attack by hard-forking to change the PoW algorithm, thereby "bricking" all ASICs (the attacker's and honest miners'!). But if the attacker is willing to suffer that initial expense, after that point the situation reverts to the GPU case (as there is not enough time to build and distribute ASICs for the new algorithm), and so from there the attacker can cheaply continue the spawn camp inevitably.In the PoS case, however, things are much brighter. For certain kinds of 51% attacks (particularly, reverting finalized blocks), there is a built-in "slashing" mechanism in the proof of stake consensus by which a large portion of the attacker's stake (and no one else's stake) can get automatically destroyed. For other, harder-to-detect attacks (notably, a 51% coalition censoring everyone else), the community can coordinate on a minority user-activated soft fork (UASF) in which the attacker's funds are once again largely destroyed (in Ethereum, this is done via the "inactivity leak mechanism"). No explicit "hard fork to delete coins" is required; with the exception of the requirement to coordinate on the UASF to select a minority block, everything else is automated and simply following the execution of the protocol rules.Hence, attacking the chain the first time will cost the attacker many millions of dollars, and the community will be back on their feet within days. Attacking the chain the second time will still cost the attacker many millions of dollars, as they would need to buy new coins to replace their old coins that were burned. And the third time will... cost even more millions of dollars. The game is very asymmetric, and not in the attacker's favor.Proof of stake is more decentralized than ASICsGPU-based proof of work is reasonably decentralized; it is not too hard to get a GPU. But GPU-based mining largely fails on the "security against attacks" criterion that we mentioned above. ASIC-based mining, on the other hand, requires millions of dollars of capital to get into (and if you buy an ASIC from someone else, most of the time, the manufacturing company gets the far better end of the deal).This is also the correct answer to the common "proof of stake means the rich get richer" argument: ASIC mining also means the rich get richer, and that game is even more tilted in favor of the rich. At least in PoS the minimum needed to stake is quite low and within reach of many regular people.Additionally, proof of stake is more censorship resistant. GPU mining and ASIC mining are both very easy to detect: they require huge amounts of electricity consumption, expensive hardware purchases and large warehouses. PoS staking, on the other hand, can be done on an unassuming laptop and even over a VPN.Possible advantages of proof of workThere are two primary genuine advantages of PoW that I see, though I see these advantages as being fairly limited.Proof of stake is more like a "closed system", leading to higher wealth concentration over the long termIn proof of stake, if you have some coin you can stake that coin and get more of that coin. In proof of work, you can always earn more coins, but you need some outside resource to do so. Hence, one could argue that over the long term, proof of stake coin distributions risk becoming more and more concentrated.The main response to this that I see is simply that in PoS, the rewards in general (and hence validator revenues) will be quite low; in eth2, we are expecting annual validator rewards to equal ~0.5-2% of the total ETH supply. And the more validators are staking, the lower interest rates get. Hence, it would likely take over a century for the level of concentration to double, and on such time scales other pressures (people wanting to spend their money, distributing their money to charity or among their children, etc.) are likely to dominate.Proof of stake requires "weak subjectivity", proof of work does notSee here for the original intro to the concept of "weak subjectivity". Essentially, the first time a node comes online, and any subsequent time a node comes online after being offline for a very long duration (ie. multiple months), that node must find some third-party source to determine the correct head of the chain. This could be their friend, it could be exchanges and block explorer sites, the client developers themselves, or many other actors. PoW does not have this requirement.However, arguably this is a very weak requirement; in fact, users need to trust client developers and/or "the community" to about this extent already. At the very least, users need to trust someone (usually client developers) to tell them what the protocol is and what any updates to the protocol have been. This is unavoidable in any software application. Hence, the marginal additional trust requirement that PoS imposes is still quite low.But even if these risks do turn out to be significant, they seem to me to be much lower than the immense gains that PoS sytems get from their far greater efficiency and their better ability to handle and recover from attacks.See also: my previous pieces on proof of stake.Proof of Stake FAQ A Proof of Stake Design Philosophy

Convex and Concave Dispositions Convex and Concave Dispositions2020 Nov 08 See all posts Convex and Concave Dispositions One of the major philosophical differences that I have noticed in how people approach making large-scale decisions in the world is how they approach the age-old tradeoff of compromise versus purity. Given a choice between two alternatives, often both expressed as deep principled philosophies, do you naturally gravitate toward the idea that one of the two paths should be correct and we should stick to it, or do you prefer to find a way in the middle between the two extremes?In mathematical terms, we can rephrase this as follows: do you expect the world that we are living in, and in particular the way that it responds to the actions that we take, to fundamentally be concave or convex? Someone with a concave disposition might say things like this:"Going to the extremes has never been good for us; you can die from being too hot or too cold. We need to find the balance between the two that's just right" "If you implement only a little bit of a philosophy, you can pick the parts that have the highest benefits and the lowest risks, and avoid the parts that are more risky. But if you insist on going to the extremes, once you've picked the low-hanging fruit, you'll be forced to look harder and harder for smaller and smaller benefits, and before you know it the growing risks might outweigh the benefit of the whole thing" "The opposing philosophy probably has some value too, so we should try to combine the best parts of both, and definitely avoid doing things that the opposing philosophy considers to be extremely terrible, just in case" Someone with a convex disposition might say things like this:"We need to focus. Otherwise, we risk becoming a jack of all trades, master of none" "If we take even a few steps down that road, it will become slippery slope and only pull us down ever further until we end up in the abyss. There's only two stable positions on the slope: either we're down there, or we stay up here" "If you give an inch, they will take a mile" "Whether we're following this philosophy or that philosophy, we should be following some philosophy and just stick to it. Making a wishy-washy mix of everything doesn't make sense" I personally find myself perenially more sympathetic to the concave approach than the convex approach, across a wide variety of contexts. If I had to choose either (i) a coin-flip between anarcho-capitalism and Soviet communism or (ii) a 50/50 compromise between the two, I would pick the latter in a heartbeat. I argued for moderation in Bitcoin block size debates, arguing against both 1-2 MB small blocks and 128 MB "very big blocks". I've argued against the idea that freedom and decentralization are "you either have it or you don't" properties with no middle ground. I argued in favor of the DAO fork, but to many people's surprise I've argued since then against similar "state-intervention" hard forks that were proposed more recently. As I said in 2019, "support for Szabo's law [blockchain immutability] is a spectrum, not a binary".But as you can probably tell by the fact that I needed to make those statements at all, not everyone seems to share the same broad intuition. I would particularly argue that the Ethereum ecosystem in general has a fundamentally concave temperament, while the Bitcoin ecosystem's temperament is much more fundamentally convex. In Bitcoin land, you can frequently hear arguments that, for example, either you have self-sovereignty or you don't, or that any system must have either a fundamentally centralizing or a fundamentally decentralizing tendency, with no possibility halfway in between.The occasional half-joking support for Tron is a key example: from my own concave point of view, if you value decentralization and immutability, you should recognize that while the Ethereum ecosystem does sometimes violate purist conceptions of these values, Tron violates them far more egregiously and without remorse, and so Ethereum is still by far the more palatable of the two options. But from a convex point of view, the extremeness of Tron's violations of these norms is a virtue: while Ethereum half-heartedly pretends to be decentralized, Tron is centralized but at least it's proud and honest about it.This difference between concave and convex mindsets is not at all limited to arcane points about efficiency/decentralization tradeoffs in cryptocurrencies. It applies to politics (guess which side has more outright anarcho-capitalists), other choices in technology, and even what food you eat. But in all of these questions too, I personally find myself fairly consistently coming out on the side of balance.Being concave about concavityBut it's worth noting that even on the meta-level, concave temperament is something that one must take great care to avoid being extreme about. There are certainly situations where policy A gives a good result, policy B gives a worse but still tolerable result, but a half-hearted mix between the two is worst of all. The coronavirus is perhaps an excellent example: a 100% effective travel ban is far more than twice as useful as a 50% effective travel ban. An effective lockdown that pushes the R0 of the virus down below 1 can eradicate the virus, leading to a quick recovery, but a half-hearted lockdown that only pushes the R0 down to 1.3 leads to months of agony with little to show for it. This is one possible explanation for why many Western countries responded poorly to it: political systems designed for compromise risk falling into middle approaches even when they are not effective.Another example is a war: if you invade country A, you conquer country A, if you invade country B, you conquer country B, but if you invade both at the same time sending half your soldiers to each one, the power of the two combined will crush you. In general, problems where the effect of a response is convex are often places where you can find benefits of some degree of centralization.But there are also many places where a mix is clearly better than either extreme. A common example is the question of setting tax rates. In economics there is the general principle that deadweight loss is quadratic: that is, the harms from the inefficiency of a tax are proportional to the square of the tax rate. The reason why this is the case can be seen as follows. A tax rate of 2% deters very few transactions, and even the transactions it deters are not very valuable - how valuable can a transaction be if a mere 2% tax is enough to discourage the participants from making it? A tax rate of 20% would deter perhaps ten times more transactions, but each individual transaction that was deterred is itself ten times more valuable to its participants than in the 2% case. Hence, a 10x higher tax may cause 100x higher economic harm. And for this reason, a low tax is generally better than a coin flip between high tax and no tax.By similar economic logic, an outright prohibition on some behavior may cause more than twice as much harm as a tax set high enough to only deter half of people from participating. Replacing existing prohibitions with medium-high punitive taxes (a very concave-temperamental thing to do) could increase efficiency, increase freedom and provide valuable revenue to build public goods or help the impoverished.Another example of effects like this in Laffer curve: a tax rate of zero raises no revenue, a tax rate of 100% raises no revenue because no one bothers to work, but some tax rate in the middle raises the most revenue. There are debates about what that revenue-maximizing rate is, but in general there's broad agreement that the chart looks something like this: If you had to pick either the average of two proposed tax plans, or a coin-flip between them, it's obvious that the average is usually best. And taxes are not the only phenomenon that are like this; economics studies a wide array of "diminishing returns" phenomena which occur everywhere in production, consumption and many other aspects of regular day-to-day behavior. Finally, a common flip-side of diminishing returns is accelerating costs: to give one notable example, if you take standard economic models of utility of money, they directly imply that double the economic inequality can cause four times the harm.The world has more than one dimensionAnother point of complexity is that in the real world, policies are not just single-dimensional numbers. There are many ways to average between two different policies, or two different philosophies. One easy example to see this is: suppose that you and your friend want to live together, but you want to live in Toronto and your friend wants to live in New York. How would you compromise between these two options?Well, you could take the geographic compromise, and enjoy your peaceful existence at the arithmetic midpoint between the two lovely cities at.... This Assembly of God church about 29km southwest of Ithaca, NY.Or you could be even more mathematically pure, and take the straight-line midpoint between Toronto and New York without even bothering to stay on the Earth's surface. Then, you're still pretty close to that church, but you're six kilometers under it. A different way to compromise is spending six months every year in Toronto and six months in New York - and this may well be an actually reasonable path for some people to take.The point is, when the options being presented to you are more complicated than simple single-dimensional numbers, figuring out how to compromise between the options well, and really take the best parts of both and not the worst parts of both, is an art, and a challenging one.And this is to be expected: "convex" and "concave" are terms best suited to mathematical functions where the input and the output are both one-dimensional. The real world is high-dimensional - and as machine-learning researchers have now well established, in high-dimensional environments the most common setting that you can expect to find yourself in is not a universally convex or universally concave one, but rather a saddle point: a point where the local region is convex in some directions but concave in other directions. A saddle point. Convex left-to-right, concave forward-to-backward.This is probably the best mathematical explanation for why both of these dispositions are to some extent necessary: the world is not entirely convex, but it is not entirely concave either. But the existence of some concave path between any two distant positions A and B is very likely, and if you can find that path then you can often find a synthesis between the two positions that is better than both.

Gitcoin Grants Round 7 Retrospective Gitcoin Grants Round 7 Retrospective2020 Oct 18 See all posts Gitcoin Grants Round 7 Retrospective Round 7 of Gitcoin Grants has successfully completed! This round has seen an unprecedented growth in interest and contributions, with $274,830 in contributions and $450,000 in matched funds distributed across 857 projects.The category structure was once again changed; this time was had a split between "dapp tech", "infrastructure tech" and "community". Here are the results: Defi joins the matching!In this round, we were able to have much higher matching values than before. This was because the usual matchings, provided by the Ethereum Foundation and a few other actors, were supplemented for the first time by a high level of participation from various defi projects:The matchers were:Chainlink, a smart contract oracle project Optimism, a layer-2 optimistic rollup The Ethereum Foundation Balancer, a decentralized exchange Synthetix, a synthetic assets platform Yearn, a collateralized-lending platform Three Arrows Capital, an investment fund Defiance Capital, another investment fund Future Fund, which is totally not an investment fund! (/s) $MEME, a memecoin Yam, a defi project Some individual contributors: ferretpatrol, bantg, Mariano Conti, Robert Leshner, Eric Conner, 10b576da0 The projects together contributed a large amount of matching funding, some of which was used this round and some of which is reserved as a "rainy day fund" for future rounds in case future matchers are less forthcoming.This is a significant milestone for the ecosystem because it shows that Gitcoin Grants is expanding beyond reliance on a very small number of funders, and is moving toward something more sustainable. But it is worth exploring, what exactly is driving these matchers to contribute, and is it sustainable?There are a few possibile motivations that are likely all in play to various extents:People are naturally altruistic to some extent, and this round defi projects got unexpectedly wealthy for the first time due to a rapid rise in interest and token prices, and so donating some of that windfall felt like a natural "good thing to do" Many in the community are critical of defi projects by default, viewing them as unproductive casinos that create a negative image of what Ethereum is supposed to be about. Contributing to public goods is an easy way for a defi project to show that they want to be a positive contributor to the ecosystem and make it better Even in the absence of such negative perceptions, defi is a competitive market that is heavily dependent on community support and network effects, and so it's very valuable to a project to win friends in the ecosystem The largest defi projects capture enough of the benefit from these public goods that it's in their own interest to contribute There's a high degree of common-ownership between defi projects (holders of one token also hold other tokens and hold ETH), and so even if it's not strictly in a project's interest to donate a large amount, token holders of that project push the project to contribute because they as holders benefit from the gains to both that project but also to the other projects whose tokens they hold. The remaining question is, of course: how sustainable will these incentives be? Are the altruistic and public-relations incentives only large enough for a one-time burst of donations of this size, or could it become more sustainable? Could we reliably expect to see, say, $2-3 million per year spent on quadratic funding matching from here on? If so, it would be excellent news for public goods funding diversification and democratization in the Ethereum ecosystem.Where did the troublemakers go?One curious result from the previous round and this round is that the "controversial" community grant recipients from previous rounds seem to have dropped in prominence on their own. In theory, we should have seen them continue to get support from their supporters with their detractors being able to do nothing about it. In practice, though, the top media recipients this round appear to be relatively uncontroversial and universally beloved mainstays of the Ethereum ecosystem. Even the Zero Knowledge Podcast, an excellent podcast but one aimed for a relatively smaller and more highly technical audience, has received a large contribution this round.What happened? Why did the distribution of media recipients improve in quality all on its own? Is the mechanism perhaps more self-correcting than we had thought?OverpaymentThis round is the first round where top recipients on all sides received quite a large amount. On the infrastructure side, the White Hat Hacking project (basically a fund to donate to samczsun) received a total of $39,258, and the Bankless podcast got $47,620. We could ask the question: are the top recipients getting too much funding?To be clear, I do think that it's very improper to try to create a moral norm that public goods contributors should only be earning salaries up to a certain level and should not be able to earn much more than that. People launching coins earn huge windfalls all the time; it is completely natural and fair for public goods contributors to also get that possibility (and furthermore, the numbers from this round translate to about ~$200,000 per year, which is not even that high).However, one can ask a more limited and pragmatic question: given the current reward structure, is putting an extra $1 into the hands of a top contributor less valuable than putting $1 into the hands of one of the other very valuable projects that's still underfunded? Turbogeth, Nethermind, RadicalXChange and many other projects could still do quite a lot with a marginal dollar. For the first time, the matching amounts are high enough that this is actually a significant issue.Especially if matching amounts increase even further, is the ecosystem going to be able to correctly allocate funds and avoid overfunding projects? Alternatively, if it fails to avoid over-concentrating funds, is that all that bad? Perhaps the possibility of becoming the center of attention for one round and earning a $500,000 windfall will be part of the incentive that motivates independent public goods contributors!We don't know; but these are the yet-unknown facts that running the experiment at its new increased scale is for the first time going to reveal.Let's talk about categories...The concept of categories as it is currently implemented in Gitcoin Grants is a somewhat strange one. Each category has a fixed total matching amount that is split between projects within that category. What this mechanism basically says is that the community can be trusted to choose between projects within a category, but we need a separate technocratic judgement to judge how the funds are split between the different categories in the first place.But it gets more paradoxical from here. In Round 7, a "collections" feature was introduced halfway through the round:If you click "Add to Cart" on a collection, you immediately add everything in the collection to your cart. This is strange because this mechanism seems to send the exact opposite message: users that don't understand the details well can choose to allocate funds to entire categories, but (unless they manually edit the amounts) they should not be making many active decisions within each category.Which is it? Do we trust the radical quadratic fancy democracy to allocate within categories but not between them, do we trust it to allocate between categories but nudge people away from making fine-grained decisions within them, or something else entirely? I recommend that for Round 8 we think harder about the philosophical challenges here and come up with a more principled approach.One option would be to have one matching pool and have all the categories just be a voluntary UI layer. Another would be to experiment with even more "affirmative action" to bootstrap particular categories: for example, we could split the Community matching into a $25,000 matching pool for each major world region (eg. North America + Oceania, Latin America, Europe, Africa, Middle East, India, East + Southeast Asia) to try to give projects in more neglected areas a leg up. There are many possibilities here! One hybrid route is that the "focused" pools could themselves be quadratic funded in the previous round!Identity verificationAs collusion, fake accounts and other attacks on Gitcoin Grants have been recently increasing, Round 7 added an additional verification option with the decentralized social-graph-based BrightID, and single-handedly boosted the project's userbase by a factor of ten:This is good, because along with helping BrightID's growth, it also subjects the project to a trial-by-fire: there's now a large incentive to try to create a large number of fake accounts on it! BrightID is going to face a tough challenge making it reasonably easy for regular users to join but at the same time resist attacks from fake and duplicate accounts. I look forward to seeing them try to meet the challenge!ZK rollups for scalabilityFinally, Round 7 was the first round where Gitcoin Grants experimented with using the ZkSync ZK rollup to decrease fees for payments: The main thing to report here is simply that the ZK rollup successfully did decrease fees! The user experience worked well. Many optimistic and ZK rollup projects are now looking at collaborating with wallets on direct integrations, which should increase the usability and security of such techniques further.ConclusionsRound 7 has been a pivotal round for Gitcoin Grants. The matching funding has become much more sustainable. The levels of funding are now large enough to successfully fund quadratic freelancers to the point where a project getting "too much funding" is a conceivable thing to worry about! Identity verification is taking steps forward. Payments have become much more efficient with the introduction of the ZkSync ZK rollup. I look forward to seeing the grants continue for many more rounds in the future.

Trust Models Trust Models2020 Aug 20 See all posts Trust Models One of the most valuable properties of many blockchain applications is trustlessness: the ability of the application to continue operating in an expected way without needing to rely on a specific actor to behave in a specific way even when their interests might change and push them to act in some different unexpected way in the future. Blockchain applications are never fully trustless, but some applications are much closer to being trustless than others. If we want to make practical moves toward trust minimization, we want to have the ability to compare different degrees of trust.First, my simple one-sentence definition of trust: trust is the use of any assumptions about the behavior of other people. If before the pandemic you would walk down the street without making sure to keep two meters' distance from strangers so that they could not suddenly take out a knife and stab you, that's a kind of trust: both trust that people are very rarely completely deranged, and trust that the people managing the legal system continue to provide strong incentives against that kind of behavior. When you run a piece of code written by someone else, you trust that they wrote the code honestly (whether due to their own sense of decency or due to an economic interest in maintaining their reputations), or at least that there exist enough people checking the code that a bug would be found. Not growing your own food is another kind of trust: trust that enough people will realize that it's in their interests to grow food so they can sell it to you. You can trust different sizes of groups of people, and there are different kinds of trust.For the purposes of analyzing blockchain protocols, I tend to break down trust into four dimensions:How many people do you need to behave as you expect? Out of how many? What kinds of motivations are needed for those people to behave? Do they need to be altruistic, or just profit seeking? Do they need to be uncoordinated? How badly will the system fail if the assumptions are violated? For now, let us focus on the first two. We can draw a graph: The more green, the better. Let us explore the categories in more detail:1 of 1: there is exactly one actor, and the system works if (and only if) that one actor does what you expect them to. This is the traditional "centralized" model, and it is what we are trying to do better than. N of N: the "dystopian" world. You rely on a whole bunch of actors, all of whom need to act as expected for everything to work, with no backups if any of them fail. N/2 of N: this is how blockchains work - they work if the majority of the miners (or PoS validators) are honest. Notice that N/2 of N becomes significantly more valuable the larger the N gets; a blockchain with a few miners/validators dominating the network is much less interesting than a blockchain with its miners/validators widely distributed. That said, we want to improve on even this level of security, hence the concern around surviving 51% attacks. 1 of N: there are many actors, and the system works as long as at least one of them does what you expect them to. Any system based on fraud proofs falls into this category, as do trusted setups though in that case the N is often smaller. Note that you do want the N to be as large as possible! Few of N: there are many actors, and the system works as long as at least some small fixed number of them do what you expect them do. Data availability checks fall into this category. 0 of N: the systems works as expected without any dependence whatsoever on external actors. Validating a block by checking it yourself falls into this category. While all buckets other than "0 of N" can be considered "trust", they are very different from each other! Trusting that one particular person (or organization) will work as expected is very different from trusting that some single person anywhere will do what you expect them to. "1 of N" is arguably much closer to "0 of N" than it is to "N/2 of N" or "1 of 1". A 1-of-N model might perhaps feel like a 1-of-1 model because it feels like you're going through a single actor, but the reality of the two is very different: in a 1-of-N system, if the actor you're working with at the moment disappears or turns evil, you can just switch to another one, whereas in a 1-of-1 system you're screwed.Particularly, note that even the correctness of the software you're running typically depends on a "few of N" trust model to ensure that if there's bugs in the code someone will catch them. With that fact in mind, trying really hard to go from 1 of N to 0 of N on some other aspect of an application is often like making a reinforced steel door for your house when the windows are open.Another important distinction is: how does the system fail if your trust assumption is violated? In blockchains, two most common types of failure are liveness failure and safety failure. A liveness failure is an event in which you are temporarily unable to do something you want to do (eg. withdraw coins, get a transaction included in a block, read information from the blockchain). A safety failure is an event in which something actively happens that the system was meant to prevent (eg. an invalid block gets included in a blockchain).Here are a few examples of trust models of a few blockchain layer 2 protocols. I use "small N" to refer to the set of participants of the layer 2 system itself, and "big N" to refer to the participants of the blockchain; the assumption is always that the layer 2 protocol has a smaller community than the blockchain itself. I also limit my use of the word "liveness failure" to cases where coins are stuck for a significant amount of time; no longer being able to use the system but being able to near-instantly withdraw does not count as a liveness failure.Channels (incl state channels, lightning network): 1 of 1 trust for liveness (your counterparty can temporarily freeze your funds, though the harms of this can be mitigated if you split coins between multiple counterparties), N/2 of big-N trust for safety (a blockchain 51% attack can steal your coins) Plasma (assuming centralized operator): 1 of 1 trust for liveness (the operator can temporarily freeze your funds), N/2 of big-N trust for safety (blockchain 51% attack) Plasma (assuming semi-decentralized operator, eg. DPOS): N/2 of small-N trust for liveness, N/2 of big-N trust for safety Optimistic rollup: 1 of 1 or N/2 of small-N trust for liveness (depends on operator type), N/2 of big-N trust for safety ZK rollup: 1 of small-N trust for liveness (if the operator fails to include your transaction, you can withdraw, and if the operator fails to include your withdrawal immediately they cannot produce more batches and you can self-withdraw with the help of any full node of the rollup system); no safety failure risks ZK rollup (with light-withdrawal enhancement): no liveness failure risks, no safety failure risks Finally, there is the question of incentives: does the actor you're trusting need to be very altruistic to act as expected, only slightly altruistic, or is being rational enough? Searching for fraud proofs is "by default" slightly altruistic, though just how altruistic it is depends on the complexity of the computation (see the verifier's dilemma), and there are ways to modify the game to make it rational.Assisting others with withdrawing from a ZK rollup is rational if we add a way to micro-pay for the service, so there is really little cause for concern that you won't be able to exit from a rollup with any significant use. Meanwhile, the greater risks of the other systems can be alleviated if we agree as a community to not accept 51% attack chains that revert too far in history or censor blocks for too long.Conclusion: when someone says that a system "depends on trust", ask them in more detail what they mean! Do they mean 1 of 1, or 1 of N, or N/2 of N? Are they demanding these participants be altruistic or just rational? If altruistic, is it a tiny expense or a huge expense? And what if the assumption is violated - do you just need to wait a few hours or days, or do you have assets that are stuck forever? Depending on the answers, your own answer to whether or not you want to use that system might be very different.

Coordination, Good and Bad Coordination, Good and Bad2020 Sep 11 See all posts Coordination, Good and Bad Special thanks to Karl Floersch and Jinglan Wang for feedback and reviewSee also:On Collusion Engineering Security Through Coordination Problems Trust Models The Meaning Of Decentralization Coordination, the ability for large groups of actors to work together for their common interest, is one of the most powerful forces in the universe. It is the difference between a king comfortably ruling a country as an oppressive dictatorship, and the people coming together and overthrowing him. It is the difference between the global temperature going up 3-5'C and the temperature going up by a much smaller amount if we work together to stop it. And it is the factor that makes companies, countries and any social organization larger than a few people possible at all.Coordination can be improved in many ways: faster spread of information, better norms that identify what behaviors are classified as cheating along with more effective punishments, stronger and more powerful organizations, tools like smart contracts that allow interactions with reduced levels of trust, governance technologies (voting, shares, decision markets...), and much more. And indeed, we as a species are getting better at all of these things with each passing decade.But there is also a very philosophically counterintuitive dark side to coordination. While it is emphatically true that "everyone coordinating with everyone" leads to much better outcomes than "every man for himself", what that does NOT imply is that each individual step toward more coordination is necessarily beneficial. If coordination is improved in an unbalanced way, the results can easily be harmful.We can think about this visually as a map, though in reality the map has many billions of "dimensions" rather than two: The bottom-left corner, "every man for himself", is where we don't want to be. The top-right corner, total coordination, is ideal, but likely unachievable. But the landscape in the middle is far from an even slope up, with many reasonably safe and productive places that it might be best to settle down in and many deep dark caves to avoid.Now what are these dangerous forms of partial coordination, where someone coordinating with some fellow humans but not others leads to a deep dark hole? It's best to describe them by giving examples:Citizens of a nation valiantly sacrificing themselves for the greater good of their country in a war.... when that country turns out to be WW2-era Germany or Japan A lobbyist giving a politician a bribe in exchange for that politician adopting the lobbyist's preferred policies Someone selling their vote in an election All sellers of a product in a market colluding to raise their prices at the same time Large miners of a blockchain colluding to launch a 51% attack In all of the above cases, we see a group of people coming together and cooperating with each other, but to the great detriment of some group that is outside the circle of coordination, and thus to the net detriment of the world as a whole. In the first case, it's all the people that were the victims of the aforementioned nations' aggression that are outside the circle of coordination and suffer heavily as a result; in the second and third cases, it's the people affected by the decisions that the corrupted voter and politician are making, in the fourth case it's the customers, and in the fifth case it's the non-participating miners and the blockchain's users. It's not an individual defecting against the group, it's a group defecting against a broader group, often the world as a whole.This type of partial coordination is often called "collusion", but it's important to note that the range of behaviors that we are talking about is quite broad. In normal speech, the word "collusion" tends to be used more often to describe relatively symmetrical relationships, but in the above cases there are plenty of examples with a strong asymmetric character. Even extortionate relationships ("vote for my preferred policies or I'll publicly reveal your affair") are a form of collusion in this sense. In the rest of this post, we'll use "collusion" to refer to "undesired coordination" generally.Evaluate Intentions, Not Actions (!!)One important property of especially the milder cases of collusion is that one cannot determine whether or not an action is part of an undesired collusion just by looking at the action itself. The reason is that the actions that a person takes are a combination of that person's internal knowledge, goals and preferences together with externally imposed incentives on that person, and so the actions that people take when colluding, versus the actions that people take on their own volition (or coordinating in benign ways) often overlap.For example, consider the case of collusion between sellers (a type of antitrust violation). If operating independently, each of three sellers might set a price for some product between $5 and $10; the differences within the range reflect difficult-to-see factors such as the seller's internal costs, their own willingness to work at different wages, supply-chain issues and the like. But if the sellers collude, they might set a price between $8 and $13. Once again, the range reflects different possibilities regarding internal costs and other difficult-to-see factors. If you see someone selling that product for $8.75, are they doing something wrong? Without knowing whether or not they coordinated with other sellers, you can't tell! Making a law that says that selling that product for more than $8 would be a bad idea; maybe there are legitimate reasons why prices have to be high at the current time. But making a law against collusion, and successfully enforcing it, gives the ideal outcome - you get the $8.75 price if the price has to be that high to cover sellers' costs, but you don't get that price if the factors driving prices up naturally are low.This applies in the bribery and vote selling cases too: it may well be the case that some people vote for the Orange Party legitimately, but others vote for the Orange Party because they were paid to. From the point of view of someone determining the rules for the voting mechanism, they don't know ahead of time whether the Orange Party is good or bad. But what they do know is that a vote where people vote based on their honest internal feelings works reasonably well, but a vote where voters can freely buy and sell their votes works terribly. This is because vote selling has a tragedy-of-the-commons: each voter only gains a small portion of the benefit from voting correctly, but would gain the full bribe if they vote the way the briber wants, and so the required bribe to lure each individual voter is far smaller than the bribe that would actually compensate the population for the costs of whatever policy the briber wants. Hence, votes where vote selling is permitted quickly collapse into plutocracy.Understanding the Game TheoryWe can zoom further out and look at this from the perspective of game theory. In the version of game theory that focuses on individual choice - that is, the version that assumes that each participant makes decisions independently and that does not allow for the possibility of groups of agents working as one for their mutual benefit, there are mathematical proofs that at least one stable Nash equilibrium must exist in any game. In fact, mechanism designers have a very wide latitude to "engineer" games to achieve specific outcomes. But in the version of game theory that allows for the possibility of coalitions working together (ie. "colluding"), called cooperative game theory, we can prove that there are large classes of games that do not have any stable outcome (called a "core"). In such games, whatever the current state of affairs is, there is always some coalition that can profitably deviate from it.One important part of that set of inherently unstable games is majority games. A majority game is formally described as a game of agents where any subset of more than half of them can capture a fixed reward and split it among themselves - a setup eerily similar to many situations in corporate governance, politics and many other situations in human life. That is to say, if there is a situation with some fixed pool of resources and some currently established mechanism for distributing those resources, and it's unavoidably possible for 51% of the participants can conspire to seize control of the resources, no matter what the current configuration is there is always some conspiracy that can emerge that would be profitable for the participants. However, that conspiracy would then in turn be vulnerable to potential new conspiracies, possibly including a combination of previous conspirators and victims... and so on and so forth. Round A B C 1 1/3 1/3 1/3 2 1/2 1/2 0 3 2/3 0 1/3 4 0 1/3 2/3 This fact, the instability of majority games under cooperative game theory, is arguably highly underrated as a simplified general mathematical model of why there may well be no "end of history" in politics and no system that proves fully satisfactory; I personally believe it's much more useful than the more famous Arrow's theorem, for example.Note once again that the core dichotomy here is not "individual versus group"; for a mechanism designer, "individual versus group" is surprisingly easy to handle. It's "group versus broader group" that presents the challenge.Decentralization as Anti-CollusionBut there is another, brighter and more actionable, conclusion from this line of thinking: if we want to create mechanisms that are stable, then we know that one important ingredient in doing so is finding ways to make it more difficult for collusions, especially large-scale collusions, to happen and to maintain themselves. In the case of voting, we have the secret ballot - a mechanism that ensures that voters have no way to prove to third parties how they voted, even if they want to prove it (MACI is one project trying to use cryptography to extend secret-ballot principles to an online context). This disrupts trust between voters and bribers, heavily restricting undesired collusions that can happen. In that case of antitrust and other corporate malfeasance, we often rely on whistleblowers and even give them rewards, explicitly incentivizing participants in a harmful collusion to defect. And in the case of public infrastructure more broadly, we have that oh-so-important concept: decentralization.One naive view of why decentralization is valuable is that it's about reducing risk from single points of technical failure. In traditional "enterprise" distributed systems, this is often actually true, but in many other cases we know that this is not sufficient to explain what's going on. It's instructive here to look at blockchains. A large mining pool publicly showing how they have internally distributed their nodes and network dependencies doesn't do much to calm community members scared of mining centralization. And pictures like these, showing 90% of Bitcoin hashpower at the time being capable of showing up to the same conference panel, do quite a bit to scare people: But why is this image scary? From a "decentralization as fault tolerance" view, large miners being able to talk to each other causes no harm. But if we look at "decentralization" as being the presence of barriers to harmful collusion, then the picture becomes quite scary, because it shows that those barriers are not nearly as strong as we thought. Now, in reality, the barriers are still far from zero; the fact that those miners can easily perform technical coordination and likely are all in the same Wechat groups does not, in fact, mean that Bitcoin is "in practice little better than a centralized company".So what are the remaining barriers to collusion? Some major ones include:Moral Barriers. In Liars and Outliers, Bruce Schneier reminds us that many "security systems" (locks on doors, warning signs reminding people of punishments...) also serve a moral function, reminding potential misbehavers that they are about to conduct a serious transgression and if they want to be a good person they should not do that. Decentralization arguably serves that function. Internal negotiation failure. The individual companies may start demanding concessions in exchange for participating in the collusion, and this could lead to negotiation stalling outright (see "holdout problems" in economics). Counter-coordination. The fact that a system is decentralized makes it easy for participants not participating in the collusion to make a fork that strips out the colluding attackers and continue the system from there. Barriers for users to join the fork are low, and the intention of decentralization creates moral pressure in favor of participating in the fork. Risk of defection. It still is much harder for five companies to join together to do something widely considered to be bad than it is for them to join together for a non-controversial or benign purpose. The five companies do not know each other too well, so there is a risk that one of them will refuse to participate and blow the whistle quickly, and the participants have a hard time judging the risk. Individual employees within the companies may blow the whistle too. Taken together, these barriers are substantial indeed - often substantial enough to stop potential attacks in their tracks, even when those five companies are simultaneously perfectly capable of quickly coordinating to do something legitimate. Ethereum blockchain miners, for example, are perfectly capable of coordinating increases to the gas limit, but that does not mean that they can so easily collude to attack the chain.The blockchain experience shows how designing protocols as institutionally decentralized architectures, even when it's well-known ahead of time that the bulk of the activity will be dominated by a few companies, can often be a very valuable thing. This idea is not limited to blockchains; it can be applied in other contexts as well (eg. see here for applications to antitrust).Forking as Counter-CoordinationBut we cannot always effectively prevent harmful collusions from taking place. And to handle those cases where a harmful collusion does take place, it would be nice to make systems that are more robust against them - more expensive for those colluding, and easier to recover for the system.There are two core operating principles that we can use to achieve this end: (1) supporting counter-coordination and (2) skin-in-the-game. The idea behind counter-coordination is this: we know that we cannot design systems to be passively robust to collusions, in large part because there is an extremely large number of ways to organize a collusion and there is no passive mechanism that can detect them, but what we can do is actively respond to collusions and strike back.In digital systems such as blockchains (this could also be applied to more mainstream systems, eg. DNS), a major and crucially important form of counter-coordination is forking. If a system gets taken over by a harmful coalition, the dissidents can come together and create an alternative version of the system, which has (mostly) the same rules except that it removes the power of the attacking coalition to control the system. Forking is very easy in an open-source software context; the main challenge in creating a successful fork is usually gathering the legitimacy (game-theoretically viewed as a form of "common knowledge") needed to get all those who disagree with the main coalition's direction to follow along with you.This is not just theory; it has been accomplished successfully, most notably in the Steem community's rebellion against a hostile takeover attempt, leading to a new blockchain called Hive in which the original antagonists have no power.Markets and Skin in the GameAnother class of collusion-resistance strategy is the idea of skin in the game. Skin in the game, in this context, basically means any mechanism that holds individual contributors in a decision individually accountable for their contributions. If a group makes a bad decision, those who approved the decision must suffer more than those who attempted to dissent. This avoids the "tragedy of the commons" inherent in voting systems.Forking is a powerful form of counter-coordination precisely because it introduces skin in the game. In Hive, the community fork of Steem that threw off the hostile takeover attempt, the coins that were used to vote in favor of the hostile takeover were largely deleted in the new fork. The key individuals who participated in the attack individually suffered as a result.Markets are in general very powerful tools precisely because they maximize skin in the game. Decision markets (prediction markets used to guide decisions; also called futarchy) are an attempt to extend this benefit of markets to organizational decision-making. That said, decision markets can only solve some problems; in particular, they cannot tell us what variables we should be optimizing for in the first place.Structuring CoordinationThis all leads us to an interesting view of what it is that people building social systems do. One of the goals of building an effective social system is, in large part, determining the structure of coordination: which groups of people and in what configurations can come together to further their group goals, and which groups cannot? Different coordination structures, different outcomesSometimes, more coordination is good: it's better when people can work together to collectively solve their problems. At other times, more coordination is dangerous: a subset of participants could coordinate to disenfranchise everyone else. And at still other times, more coordination is necessary for another reason: to enable the broader community to "strike back" against a collusion attacking the system.In all three of those cases, there are different mechanisms that can be used to achieve these ends. Of course, it is very difficult to prevent communication outright, and it is very difficult to make coordination perfect. But there are many options in between that can nevertheless have powerful effects.Here are a few possible coordination structuring techniques:Technologies and norms that protect privacy Technological means that make it difficult to prove how you behaved (secret ballots, MACI and similar tech) Deliberate decentralization, distributing control of some mechanism to a wide group of people that are known to not be well-coordinated Decentralization in physical space, separating out different functions (or different shares of the same function) to different locations (eg. see Samo Burja on connections between urban decentralization and political decentralization) Decentralization between role-based constituencies, separating out different functions (or different shares of the same function) to different types of participants (eg. in a blockchain: "core developers", "miners", "coin holders", "application developers", "users") Schelling points, allowing large groups of people to quickly coordinate around a single path forward. Complex Schelling points could potentially even be implemented in code (eg. recovery from 51% attacks can benefit from this). Speaking a common language (or alternatively, splitting control between multiple constituencies who speak different languages) Using per-person voting instead of per-(coin/share) voting to greatly increase the number of people who would need to collude to affect a decision Encouraging and relying on defectors to alert the public about upcoming collusions None of these strategies are perfect, but they can be used in various contexts with differing levels of success. Additionally, these techniques can and should be combined with mechanism design that attempts to make harmful collusions less profitable and more risky to the extent possible; skin in the game is a very powerful tool in this regard. Which combination works best ultimately depends on your specific use case.