找到
227
篇与
科普知识
相关的结果
-
 A Note On Charity Through Marginal Price Discrimination A Note On Charity Through Marginal Price Discrimination2017 Mar 11 See all posts A Note On Charity Through Marginal Price Discrimination Updated 2018-07-28. See end note.The following is an interesting idea that I had two years ago that I personally believe has promise and could be easily implemented in the context of a blockchain ecosystem, though if desired it could certainly also be implemented with more traditional technologies (blockchains would help get the scheme network effects by putting the core logic on a more neutral platform).Suppose that you are a restaurant selling sandwiches, and you ordinarily sell sandwiches for $7.50. Why did you choose to sell them for $7.50, and not $7.75 or $7.25? It clearly can't be the case that the cost of production is exactly $7.49999, as in that case you would be making no profit, and would not be able to cover fixed costs; hence, in most normal situations you would still be able to make some profit if you sold at $7.25 or $7.75, though less. Why less at $7.25? Because the price is lower. Why less at $7.75? Because you get fewer customers. It just so happens that $7.50 is the point at which the balance between those two factors is optimal for you. Notice one consequence of this: if you make a slight distortion to the optimal price, then even compared to the magnitude of the distortion the losses that you face are minimal. If you raise prices by 1%, from $7.50 to $7.575, then your profit declines from $6750 to $6733.12 - a tiny 0.25% reduction. And that's profit - if you had instead donated 1% of the price of each sandwich, it would have reduced your profit by 5%. The smaller the distortion the more favorable the ratio: raising prices by 0.2% only cuts your profits down by 0.01%.Now, you could argue that stores are not perfectly rational, and not perfectly informed, and so they may not actually be charging at optimal prices, all factors considered. However, if you don't know what direction the deviation is in for any given store, then even still, in expectation, the scheme works the same way - except instead of losing $17 it's more like flipping a coin where half the time you gain $50 and half the time you lose $84. Furthermore, in the more complex scheme that we will describe later, we'll be adjusting prices in both directions simultaneously, and so there will not even be any extra risk - no matter how correct or incorrect the original price was, the scheme will give you a predictable small net loss.Also, the above example was one where marginal costs are high, and customers are picky about prices - in the above model, charging $9 would have netted you no customers at all. In a situation where marginal costs are much lower, and customers are less price-sensitive, the losses from raising or lowering prices would be even lower.So what is the point of all this? Well, suppose that our sandwich shop changes its policy: it sells sandwiches for $7.55 to the general public, but lowers the prices to $7.35 for people who volunteered in some charity that maintains some local park (say, this is 25% of the population). The store's new profit is \(\$6682.5 \cdot 0.25+\$6742.5 \cdot 0.75=\$6727.5\) (that's a $22.5 loss), but the result is that you are now paying all 4500 of your customers 20 cents each to volunteer at that charity - an incentive size of $900 (if you just count the customers who actually do volunteer, $225). So the store loses a bit, but gets a huge amount of leverage, de-facto contributing at least $225 depending on how you measure it for a cost of only $22.5. Now, what we can start to do is build up an ecosystem of "stickers", which are non-transferable digital "tokens" that organizations hand out to people who they think are contributing to worthy causes. Tokens could be organized by category (eg. poverty relief, science research, environmental, local community projects, open source software development, writing good blogs), and merchants would be free to charge marginally lower prices to holders of the tokens that represent whatever causes they personally approve of.The next stage is to make the scheme recursive - being or working for a merchant that offers lower prices to holders of green stickers is itself enough to merit you a green sticker, albeit one that is of lower potency and gives you a lower discount. This way, if an entire community approves of a particular cause, it may actually be profit-maximizing to start offering discounts for the associated sticker, and so economic and social pressure will maintain a certain level of spending and participation toward the cause in a stable equilibrium.As far as implementation goes, this requires:A standard for stickers, including wallets where people can hold stickers Payment systems that have support for charging lower prices to sticker holders included At least a few sticker-issuing organizations (the lowest overhead is likely to be issuing stickers for charity donations, and for easily verifiable online content, eg. open source software and blogs) So this is something that can certainly be bootstrapped within a small community and user base and then let to grow over time.Update 2017.03.14: here is an economic model/simulation showing the above implemented as a Python script.Update 2018.07.28: after discussions with others (Glen Weyl and several Reddit commenters), I realized a few extra things about this mechanism, some encouraging and some worrying:The above mechanism could be used not just by charities, but also by centralized corporate actors. For example, a large corporation could offer a bribe of $40 to any store that offers the 20-cent discount to customers of its products, gaining additional revenue much higher than $40. So it's empowering but potentially dangerous in the wrong hands... (I have not researched it but I'm sure this kind of technique is used in various kinds of loyalty programs already) The above mechanism has the property that a merchant can "donate" \(\$x\) to charity at a cost of \(\$x^\) (note: \(x^
A Note On Charity Through Marginal Price Discrimination A Note On Charity Through Marginal Price Discrimination2017 Mar 11 See all posts A Note On Charity Through Marginal Price Discrimination Updated 2018-07-28. See end note.The following is an interesting idea that I had two years ago that I personally believe has promise and could be easily implemented in the context of a blockchain ecosystem, though if desired it could certainly also be implemented with more traditional technologies (blockchains would help get the scheme network effects by putting the core logic on a more neutral platform).Suppose that you are a restaurant selling sandwiches, and you ordinarily sell sandwiches for $7.50. Why did you choose to sell them for $7.50, and not $7.75 or $7.25? It clearly can't be the case that the cost of production is exactly $7.49999, as in that case you would be making no profit, and would not be able to cover fixed costs; hence, in most normal situations you would still be able to make some profit if you sold at $7.25 or $7.75, though less. Why less at $7.25? Because the price is lower. Why less at $7.75? Because you get fewer customers. It just so happens that $7.50 is the point at which the balance between those two factors is optimal for you. Notice one consequence of this: if you make a slight distortion to the optimal price, then even compared to the magnitude of the distortion the losses that you face are minimal. If you raise prices by 1%, from $7.50 to $7.575, then your profit declines from $6750 to $6733.12 - a tiny 0.25% reduction. And that's profit - if you had instead donated 1% of the price of each sandwich, it would have reduced your profit by 5%. The smaller the distortion the more favorable the ratio: raising prices by 0.2% only cuts your profits down by 0.01%.Now, you could argue that stores are not perfectly rational, and not perfectly informed, and so they may not actually be charging at optimal prices, all factors considered. However, if you don't know what direction the deviation is in for any given store, then even still, in expectation, the scheme works the same way - except instead of losing $17 it's more like flipping a coin where half the time you gain $50 and half the time you lose $84. Furthermore, in the more complex scheme that we will describe later, we'll be adjusting prices in both directions simultaneously, and so there will not even be any extra risk - no matter how correct or incorrect the original price was, the scheme will give you a predictable small net loss.Also, the above example was one where marginal costs are high, and customers are picky about prices - in the above model, charging $9 would have netted you no customers at all. In a situation where marginal costs are much lower, and customers are less price-sensitive, the losses from raising or lowering prices would be even lower.So what is the point of all this? Well, suppose that our sandwich shop changes its policy: it sells sandwiches for $7.55 to the general public, but lowers the prices to $7.35 for people who volunteered in some charity that maintains some local park (say, this is 25% of the population). The store's new profit is \(\$6682.5 \cdot 0.25+\$6742.5 \cdot 0.75=\$6727.5\) (that's a $22.5 loss), but the result is that you are now paying all 4500 of your customers 20 cents each to volunteer at that charity - an incentive size of $900 (if you just count the customers who actually do volunteer, $225). So the store loses a bit, but gets a huge amount of leverage, de-facto contributing at least $225 depending on how you measure it for a cost of only $22.5. Now, what we can start to do is build up an ecosystem of "stickers", which are non-transferable digital "tokens" that organizations hand out to people who they think are contributing to worthy causes. Tokens could be organized by category (eg. poverty relief, science research, environmental, local community projects, open source software development, writing good blogs), and merchants would be free to charge marginally lower prices to holders of the tokens that represent whatever causes they personally approve of.The next stage is to make the scheme recursive - being or working for a merchant that offers lower prices to holders of green stickers is itself enough to merit you a green sticker, albeit one that is of lower potency and gives you a lower discount. This way, if an entire community approves of a particular cause, it may actually be profit-maximizing to start offering discounts for the associated sticker, and so economic and social pressure will maintain a certain level of spending and participation toward the cause in a stable equilibrium.As far as implementation goes, this requires:A standard for stickers, including wallets where people can hold stickers Payment systems that have support for charging lower prices to sticker holders included At least a few sticker-issuing organizations (the lowest overhead is likely to be issuing stickers for charity donations, and for easily verifiable online content, eg. open source software and blogs) So this is something that can certainly be bootstrapped within a small community and user base and then let to grow over time.Update 2017.03.14: here is an economic model/simulation showing the above implemented as a Python script.Update 2018.07.28: after discussions with others (Glen Weyl and several Reddit commenters), I realized a few extra things about this mechanism, some encouraging and some worrying:The above mechanism could be used not just by charities, but also by centralized corporate actors. For example, a large corporation could offer a bribe of $40 to any store that offers the 20-cent discount to customers of its products, gaining additional revenue much higher than $40. So it's empowering but potentially dangerous in the wrong hands... (I have not researched it but I'm sure this kind of technique is used in various kinds of loyalty programs already) The above mechanism has the property that a merchant can "donate" \(\$x\) to charity at a cost of \(\$x^\) (note: \(x^ -
 Hard Forks, Soft Forks, Defaults and Coercion Hard Forks, Soft Forks, Defaults and Coercion2017 Mar 14 See all posts Hard Forks, Soft Forks, Defaults and Coercion One of the important arguments in the blockchain space is that of whether hard forks or soft forks are the preferred protocol upgrade mechanism. The basic difference between the two is that soft forks change the rules of a protocol by strictly reducing the set of transactions that is valid, so nodes following the old rules will still get on the new chain (provided that the majority of miners/validators implements the fork), whereas hard forks allow previously invalid transactions and blocks to become valid, so clients must upgrade their clients in order to stay on the hard-forked chain. There are also two sub-types of hard forks: strictly expanding hard forks, which strictly expand the set of transactions that is valid, and so effectively the old rules are a soft fork with respect to the new rules, and bilateral hard forks, where the two rulesets are incompatible both ways.Here is a Venn diagram to illustrate the fork types: The benefits commonly cited for the two are as follows.Hard forks allow the developers much more flexibility in making the protocol upgrade, as they do not have to take care to make sure that the new rules "fit into" the old rules Soft forks are more convenient for users, as users do not need to upgrade to stay on the chain Soft forks are less likely to lead to a chain split Soft forks only really require consent from miners/validators (as even if users still use the old rules, if the nodes making the chain use the new rules then only things valid under the new rules will get into the chain in any case); hard forks require opt-in consent from users Aside from this, one major criticism often given for hard forks is that hard forks are "coercive". The kind of coercion implied here is not physical force; rather, it's coercion through network effect. That is, if the network changes rules from A to B, then even if you personally like A, if most other users like B and switch to B then you have to switch to B despite your personal disapproval of the change in order to be on the same network as everyone else.Proponents of hard forks are often derided as trying to effect a "hostile take over" of a network, and "force" users to go along with them. Additionally, the risk of chain splits is often used to bill hard forks as "unsafe".It is my personal viewpoint that these criticisms are wrong, and furthermore in many cases completely backwards. This viewpoint is not specific to Ethereum, or Bitcoin, or any other blockchain; it arises out of general properties of these systems, and is applicable to any of them. Furthermore, the arguments below only apply to controversial changes, where a large portion of at least one constituency (miners/validators and users) disapprove of them; if a change is non-contentious, then it can generally be done safely no matter what the format of the fork is.First of all, let us discuss the question of coercion. Hard forks and soft forks both change the protocol in ways that some users may not like; any protocol change will do this if it has less than exactly 100% support. Furthermore, it is almost inevitable that at least some of the dissenters, in any scenario, value the network effect of sticking with the larger group more than they value their own preferences regarding the protocol rules. Hence, both fork types are coercive, in the network-effect sense of the word.However, there is an essential difference between hard forks and soft forks: hard forks are opt-in, whereas soft forks allow users no "opting" at all. In order for a user to join a hard forked chain, they must personally install the software package that implements the fork rules, and the set of users that disagrees with a rule change even more strongly than they value network effects can theoretically simply stay on the old chain - and, practically speaking, such an event has already happened.This is true in the case of both strictly expanding hard forks and bilateral hard forks. In the case of soft forks, however, if the fork succeeds the unforked chain does not exist. Hence, soft forks clearly institutionally favor coercion over secession, whereas hard forks have the opposite bias. My own moral views lead me to favor secession over coercion, though others may differ (the most common argument raised is that network effects are really really important and it is essential that "one coin rule them all", though more moderate versions of this also exist).If I had to guess why, despite these arguments, soft forks are often billed as "less coercive" than hard forks, I would say that it is because it feels like a hard fork "forces" the user into installing a software update, whereas with a soft fork users do not "have" to do anything at all. However, this intuition is misguided: what matters is not whether or not individual users have to perform the simple bureaucratic step of clicking a "download" button, but rather whether or not the user is coerced into accepting a change in protocol rules that they would rather not accept. And by this metric, as mentioned above, both kinds of forks are ultimately coercive, and it is hard forks that come out as being somewhat better at preserving user freedom.Now, let's look at highly controversial forks, particularly forks where miner/validator preferences and user preferences conflict. There are three cases here: (i) bilateral hard forks, (ii) strictly expanding hard forks, and (iii) so-called "user-activated soft forks" (UASF). A fourth category is where miners activate a soft fork without user consent; we will get to this later.First, bilateral hard forks. In the best case, the situation is simple. The two coins trade on the market, and traders decide the relative value of the two. From the ETC/ETH case, we have overwhelming evidence that miners are overwhelmingly likely to simply assign their hashrate to coins based on the ratio of prices in order to maximize their profit, regardless of their own ideological views. Even if some miners profess ideological preferences toward one side or the other, it is overwhemingly likely that there will be enough miners that are willing to arbitrage any mismatch between price ratio and hashpower ratio, and bring the two into alignment. If a cartel of miners tries to form to not mine on one chain, there are overwheming incentives to defect.There are two edge cases here. The first is the possibilty that, because of an inefficient difficulty adjustment algorithm, the value of mining the coin goes down becase price drops but difficulty does not go down to compensate, making mining very unprofitable, and there are no miners willing to mine at a loss to keep pushing the chain forward until its difficulty comes back into balance. This was not the case with Ethereum, but may well be the case with Bitcoin. Hence, the minority chain may well simply never get off the ground, and so it will die. Note that the normative question of whether or not this is a good thing depends on your views on coercion versus secession; as you can imagine from what I wrote above I personally believe that such minority-chain-hostile difficulty adjustment algorithms are bad.The second edge case is that if the disparity is very large, the large chain can 51% attack the smaller chain. Even in the case of an ETH/ETC split with a 10:1 ratio, this has not happened; so it is certainly not a given. However, it is always a possibility if miners on the dominant chain prefer coercion to allowing secession and act on these values.Next, let's look at strictly expanding hard forks. In an SEHF, there is the property that the non-forked chain is valid under the forked rules, and so if the fork has a lower price than the non-forked chain, it will have less hashpower than the non-forked chain, and so the non-forked chain will end up being accepted as the longest chain by both original-client and forked-client rules - and so the forked chain "will be annihilated".There is an argument that there is thus a strong inherent bias against such a fork succeeding, as the possibility that the forked chain will get annihiliated will be baked into the price, pushing the price lower, making it even more likely that the chain will be annihilated... This argument to me seems strong, and so it is a very good reason to make any contentious hard fork bilateral rather than strictly expanding.Bitcoin Unlimited developers suggest dealing with this problem by making the hard fork bilateral manually after it happens, but a better choice would be to make the bilaterality built-in; for example, in the bitcoin case, one can add a rule to ban some unused opcode, and then make a transaction containing that opcode on the non-forked chain, so that under the forked rules the non-forked chain will from then on be considered forever invalid. In the Ethereum case, because of various details about how state calculation works, nearly all hard forks are bilateral almost automatically. Other chains may have different properties depending on their architecture.The last type of fork that was mentioned above is the user-activated soft fork. In a UASF, users turn on the soft fork rules without bothering to get consensus from miners; miners are expected to simply fall in line out of economic interest. If many users do not go along with the UASF, then there will be a coin split, and this will lead to a scenario identical to the strictly expanding hard fork, except - and this is the really clever and devious part of the concept - the same "risk of annihilation" pressure that strongly disfavors the forked chain in a strictly expanding hard fork instead strongly favors the forked chain in a UASF. Even though a UASF is opt-in, it uses economic asymmetry in order to bias itself toward success (though the bias is not absolute; if a UASF is decidedly unpopular then it will not succeed and will simply lead to a chain split).However, UASFs are a dangerous game. For example, let us suppose that the developers of a project want to make a UASF patch that converts an unused opcode that previously accepted all transactions into an opcode that only accepts transactions that comply with the rules of some cool new feature, though one that is politically or technically controversial and miners dislike. Miners have a clever and devious way to fight back: they can unilaterally implement a miner-activated soft fork that makes all transactions using the feature created by the soft fork always fail.Now, we have three rulesets:The original rules where opcode X is always valid. The rules where opcode X is only valid if the rest of the transaction complies with the new rules The rules where opcode X is always invalid. Note that (2) is a soft-fork with respect to (1), and (3) is a soft-fork with respect to (2). Now, there is strong economic pressure in favor of (3), and so the soft-fork fails to accomplish its objective.The conclusion is this. Soft forks are a dangerous game, and they become even more dangerous if they are contentious and miners start fighting back. Strictly expanding hard forks are also a dangerous game. Miner-activated soft forks are coercive; user-activated soft forks are less coercive, though still quite coercive because of the economic pressure, and they also have their dangers. If you really want to make a contentious change, and have decided that the high social costs of doing so are worth it, just do a clean bilateral hard fork, spend some time to add some proper replay protection, and let the market sort it out.
Hard Forks, Soft Forks, Defaults and Coercion Hard Forks, Soft Forks, Defaults and Coercion2017 Mar 14 See all posts Hard Forks, Soft Forks, Defaults and Coercion One of the important arguments in the blockchain space is that of whether hard forks or soft forks are the preferred protocol upgrade mechanism. The basic difference between the two is that soft forks change the rules of a protocol by strictly reducing the set of transactions that is valid, so nodes following the old rules will still get on the new chain (provided that the majority of miners/validators implements the fork), whereas hard forks allow previously invalid transactions and blocks to become valid, so clients must upgrade their clients in order to stay on the hard-forked chain. There are also two sub-types of hard forks: strictly expanding hard forks, which strictly expand the set of transactions that is valid, and so effectively the old rules are a soft fork with respect to the new rules, and bilateral hard forks, where the two rulesets are incompatible both ways.Here is a Venn diagram to illustrate the fork types: The benefits commonly cited for the two are as follows.Hard forks allow the developers much more flexibility in making the protocol upgrade, as they do not have to take care to make sure that the new rules "fit into" the old rules Soft forks are more convenient for users, as users do not need to upgrade to stay on the chain Soft forks are less likely to lead to a chain split Soft forks only really require consent from miners/validators (as even if users still use the old rules, if the nodes making the chain use the new rules then only things valid under the new rules will get into the chain in any case); hard forks require opt-in consent from users Aside from this, one major criticism often given for hard forks is that hard forks are "coercive". The kind of coercion implied here is not physical force; rather, it's coercion through network effect. That is, if the network changes rules from A to B, then even if you personally like A, if most other users like B and switch to B then you have to switch to B despite your personal disapproval of the change in order to be on the same network as everyone else.Proponents of hard forks are often derided as trying to effect a "hostile take over" of a network, and "force" users to go along with them. Additionally, the risk of chain splits is often used to bill hard forks as "unsafe".It is my personal viewpoint that these criticisms are wrong, and furthermore in many cases completely backwards. This viewpoint is not specific to Ethereum, or Bitcoin, or any other blockchain; it arises out of general properties of these systems, and is applicable to any of them. Furthermore, the arguments below only apply to controversial changes, where a large portion of at least one constituency (miners/validators and users) disapprove of them; if a change is non-contentious, then it can generally be done safely no matter what the format of the fork is.First of all, let us discuss the question of coercion. Hard forks and soft forks both change the protocol in ways that some users may not like; any protocol change will do this if it has less than exactly 100% support. Furthermore, it is almost inevitable that at least some of the dissenters, in any scenario, value the network effect of sticking with the larger group more than they value their own preferences regarding the protocol rules. Hence, both fork types are coercive, in the network-effect sense of the word.However, there is an essential difference between hard forks and soft forks: hard forks are opt-in, whereas soft forks allow users no "opting" at all. In order for a user to join a hard forked chain, they must personally install the software package that implements the fork rules, and the set of users that disagrees with a rule change even more strongly than they value network effects can theoretically simply stay on the old chain - and, practically speaking, such an event has already happened.This is true in the case of both strictly expanding hard forks and bilateral hard forks. In the case of soft forks, however, if the fork succeeds the unforked chain does not exist. Hence, soft forks clearly institutionally favor coercion over secession, whereas hard forks have the opposite bias. My own moral views lead me to favor secession over coercion, though others may differ (the most common argument raised is that network effects are really really important and it is essential that "one coin rule them all", though more moderate versions of this also exist).If I had to guess why, despite these arguments, soft forks are often billed as "less coercive" than hard forks, I would say that it is because it feels like a hard fork "forces" the user into installing a software update, whereas with a soft fork users do not "have" to do anything at all. However, this intuition is misguided: what matters is not whether or not individual users have to perform the simple bureaucratic step of clicking a "download" button, but rather whether or not the user is coerced into accepting a change in protocol rules that they would rather not accept. And by this metric, as mentioned above, both kinds of forks are ultimately coercive, and it is hard forks that come out as being somewhat better at preserving user freedom.Now, let's look at highly controversial forks, particularly forks where miner/validator preferences and user preferences conflict. There are three cases here: (i) bilateral hard forks, (ii) strictly expanding hard forks, and (iii) so-called "user-activated soft forks" (UASF). A fourth category is where miners activate a soft fork without user consent; we will get to this later.First, bilateral hard forks. In the best case, the situation is simple. The two coins trade on the market, and traders decide the relative value of the two. From the ETC/ETH case, we have overwhelming evidence that miners are overwhelmingly likely to simply assign their hashrate to coins based on the ratio of prices in order to maximize their profit, regardless of their own ideological views. Even if some miners profess ideological preferences toward one side or the other, it is overwhemingly likely that there will be enough miners that are willing to arbitrage any mismatch between price ratio and hashpower ratio, and bring the two into alignment. If a cartel of miners tries to form to not mine on one chain, there are overwheming incentives to defect.There are two edge cases here. The first is the possibilty that, because of an inefficient difficulty adjustment algorithm, the value of mining the coin goes down becase price drops but difficulty does not go down to compensate, making mining very unprofitable, and there are no miners willing to mine at a loss to keep pushing the chain forward until its difficulty comes back into balance. This was not the case with Ethereum, but may well be the case with Bitcoin. Hence, the minority chain may well simply never get off the ground, and so it will die. Note that the normative question of whether or not this is a good thing depends on your views on coercion versus secession; as you can imagine from what I wrote above I personally believe that such minority-chain-hostile difficulty adjustment algorithms are bad.The second edge case is that if the disparity is very large, the large chain can 51% attack the smaller chain. Even in the case of an ETH/ETC split with a 10:1 ratio, this has not happened; so it is certainly not a given. However, it is always a possibility if miners on the dominant chain prefer coercion to allowing secession and act on these values.Next, let's look at strictly expanding hard forks. In an SEHF, there is the property that the non-forked chain is valid under the forked rules, and so if the fork has a lower price than the non-forked chain, it will have less hashpower than the non-forked chain, and so the non-forked chain will end up being accepted as the longest chain by both original-client and forked-client rules - and so the forked chain "will be annihilated".There is an argument that there is thus a strong inherent bias against such a fork succeeding, as the possibility that the forked chain will get annihiliated will be baked into the price, pushing the price lower, making it even more likely that the chain will be annihilated... This argument to me seems strong, and so it is a very good reason to make any contentious hard fork bilateral rather than strictly expanding.Bitcoin Unlimited developers suggest dealing with this problem by making the hard fork bilateral manually after it happens, but a better choice would be to make the bilaterality built-in; for example, in the bitcoin case, one can add a rule to ban some unused opcode, and then make a transaction containing that opcode on the non-forked chain, so that under the forked rules the non-forked chain will from then on be considered forever invalid. In the Ethereum case, because of various details about how state calculation works, nearly all hard forks are bilateral almost automatically. Other chains may have different properties depending on their architecture.The last type of fork that was mentioned above is the user-activated soft fork. In a UASF, users turn on the soft fork rules without bothering to get consensus from miners; miners are expected to simply fall in line out of economic interest. If many users do not go along with the UASF, then there will be a coin split, and this will lead to a scenario identical to the strictly expanding hard fork, except - and this is the really clever and devious part of the concept - the same "risk of annihilation" pressure that strongly disfavors the forked chain in a strictly expanding hard fork instead strongly favors the forked chain in a UASF. Even though a UASF is opt-in, it uses economic asymmetry in order to bias itself toward success (though the bias is not absolute; if a UASF is decidedly unpopular then it will not succeed and will simply lead to a chain split).However, UASFs are a dangerous game. For example, let us suppose that the developers of a project want to make a UASF patch that converts an unused opcode that previously accepted all transactions into an opcode that only accepts transactions that comply with the rules of some cool new feature, though one that is politically or technically controversial and miners dislike. Miners have a clever and devious way to fight back: they can unilaterally implement a miner-activated soft fork that makes all transactions using the feature created by the soft fork always fail.Now, we have three rulesets:The original rules where opcode X is always valid. The rules where opcode X is only valid if the rest of the transaction complies with the new rules The rules where opcode X is always invalid. Note that (2) is a soft-fork with respect to (1), and (3) is a soft-fork with respect to (2). Now, there is strong economic pressure in favor of (3), and so the soft-fork fails to accomplish its objective.The conclusion is this. Soft forks are a dangerous game, and they become even more dangerous if they are contentious and miners start fighting back. Strictly expanding hard forks are also a dangerous game. Miner-activated soft forks are coercive; user-activated soft forks are less coercive, though still quite coercive because of the economic pressure, and they also have their dangers. If you really want to make a contentious change, and have decided that the high social costs of doing so are worth it, just do a clean bilateral hard fork, spend some time to add some proper replay protection, and let the market sort it out. -
![[Mirror] Zk-SNARKs: Under the Hood](https://fastly.jsdelivr.net/npm/typecho-joe-next@6.0.0/assets/img/lazyload.jpg) [Mirror] Zk-SNARKs: Under the Hood [Mirror] Zk-SNARKs: Under the Hood2017 Feb 01 See all posts [Mirror] Zk-SNARKs: Under the Hood This is a mirror of the post at https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6This is the third part of a series of articles explaining how the technology behind zk-SNARKs works; the previous articles on quadratic arithmetic programs and elliptic curve pairings are required reading, and this article will assume knowledge of both concepts. Basic knowledge of what zk-SNARKs are and what they do is also assumed. See also Christian Reitwiessner's article here for another technical introduction.In the previous articles, we introduced the quadratic arithmetic program, a way of representing any computational problem with a polynomial equation that is much more amenable to various forms of mathematical trickery. We also introduced elliptic curve pairings, which allow a very limited form of one-way homomorphic encryption that lets you do equality checking. Now, we are going to start from where we left off, and use elliptic curve pairings, together with a few other mathematical tricks, in order to allow a prover to prove that they know a solution for a particular QAP without revealing anything else about the actual solution.This article will focus on the Pinocchio protocol by Parno, Gentry, Howell and Raykova from 2013 (often called PGHR13); there are a few variations on the basic mechanism, so a zk-SNARK scheme implemented in practice may work slightly differently, but the basic principles will in general remain the same.To start off, let us go into the key cryptographic assumption underlying the security of the mechanism that we are going to use: the *knowledge-of-exponent* assumption.Basically, if you get a pair of points \(P\) and \(Q\), where \(P \cdot k = Q\), and you get a point \(C\), then it is not possible to come up with \(C \cdot k\) unless \(C\) is "derived" from \(P\) in some way that you know. This may seem intuitively obvious, but this assumption actually cannot be derived from any other assumption (eg. discrete log hardness) that we usually use when proving security of elliptic curve-based protocols, and so zk-SNARKs do in fact rest on a somewhat shakier foundation than elliptic curve cryptography more generally — although it's still sturdy enough that most cryptographers are okay with it.Now, let's go into how this can be used. Supposed that a pair of points \((P, Q)\) falls from the sky, where \(P \cdot k = Q\), but nobody knows what the value of \(k\) is. Now, suppose that I come up with a pair of points \((R, S)\) where \(R \cdot k = S\). Then, the KoE assumption implies that the only way I could have made that pair of points was by taking \(P\) and \(Q\), and multiplying both by some factor r that I personally know. Note also that thanks to the magic of elliptic curve pairings, checking that \(R = k \cdot S\) doesn't actually require knowing \(k\) - instead, you can simply check whether or not \(e(R, Q) = e(P, S)\).Let's do something more interesting. Suppose that we have ten pairs of points fall from the sky: \((P_1, Q_1), (P_2, Q_2)... (P_, Q_)\). In all cases, \(P_i \cdot k = Q_i\). Suppose that I then provide you with a pair of points \((R, S)\) where \(R \cdot k = S\). What do you know now? You know that \(R\) is some linear combination \(P_1 \cdot i_1 + P_2 \cdot i_2 + ... + P_ \cdot i_\), where I know the coefficients \(i_1, i_2 ... i_\). That is, the only way to arrive at such a pair of points \((R, S)\) is to take some multiples of \(P_1, P_2 ... P_\) and add them together, and make the same calculation with \(Q_1, Q_2 ... Q_\).Note that, given any specific set of \(P_1...P_\) points that you might want to check linear combinations for, you can't actually create the accompanying \(Q_1...Q_\) points without knowing what \(k\) is, and if you do know what \(k\) is then you can create a pair \((R, S)\) where \(R \cdot k = S\) for whatever \(R\) you want, without bothering to create a linear combination. Hence, for this to work it's absolutely imperative that whoever creates those points is trustworthy and actually deletes \(k\) once they created the ten points. This is where the concept of a "trusted setup" comes from.Remember that the solution to a QAP is a set of polynomials \((A, B, C)\) such that \(A(x) \cdot B(x) - C(x) = H(x) \cdot Z(x)\), where:\(A\) is a linear combination of a set of polynomials \(\\) \(B\) is the linear combination of \(\\) with the same coefficients \(C\) is a linear combination of \(\\) with the same coefficients The sets \(\, \\) and \(\\) and the polynomial \(Z\) are part of the problem statement.However, in most real-world cases, \(A, B\) and \(C\) are extremely large; for something with many thousands of circuit gates like a hash function, the polynomials (and the factors for the linear combinations) may have many thousands of terms. Hence, instead of having the prover provide the linear combinations directly, we are going to use the trick that we introduced above to have the prover prove that they are providing something which is a linear combination, but without revealing anything else.You might have noticed that the trick above works on elliptic curve points, not polynomials. Hence, what actually happens is that we add the following values to the trusted setup:\(G \cdot A_1(t), G \cdot A_1(t) \cdot k_a\) \(G \cdot A_2(t), G \cdot A_2(t) \cdot k_a\) ... \(G \cdot B_1(t), G \cdot B_1(t) \cdot k_b\) \(G \cdot B_2(t), G \cdot B_2(t) \cdot k_b\) ... \(G \cdot C_1(t), G \cdot C_1(t) \cdot k_c\) \(G \cdot C_2(t), G \cdot C_2(t) \cdot k_c\) ... You can think of t as a "secret point" at which the polynomial is evaluated. \(G\) is a "generator" (some random elliptic curve point that is specified as part of the protocol) and \(t, k_a, k_b\) and \(k_c\) are "toxic waste", numbers that absolutely must be deleted at all costs, or else whoever has them will be able to make fake proofs. Now, if someone gives you a pair of points \(P\), \(Q\) such that \(P \cdot k_a = Q\) (reminder: we don't need \(k_a\) to check this, as we can do a pairing check), then you know that what they are giving you is a linear combination of \(A_i\) polynomials evaluated at \(t\).Hence, so far the prover must give:\(\pi _a = G \cdot A(t), \pi '_a = G \cdot A(t) \cdot k_a\) \(\pi _b = G \cdot B(t), \pi '_b = G \cdot B(t) \cdot k_b\) \(\pi _c = G \cdot C(t), \pi '_c = G \cdot C(t) \cdot k_c\) Note that the prover doesn't actually need to know (and shouldn't know!) \(t, k_a, k_b\) or \(k_c\) to compute these values; rather, the prover should be able to compute these values just from the points that we're adding to the trusted setup.The next step is to make sure that all three linear combinations have the same coefficients. This we can do by adding another set of values to the trusted setup: \(G \cdot (A_i(t) + B_i(t) + C_i(t)) \cdot b\), where \(b\) is another number that should be considered "toxic waste" and discarded as soon as the trusted setup is completed. We can then have the prover create a linear combination with these values with the same coefficients, and use the same pairing trick as above to verify that this value matches up with the provided \(A + B + C\).Finally, we need to prove that \(A \cdot B - C = H \cdot Z\). We do this once again with a pairing check:\(e(\pi _a, \pi _b) / e(\pi _c, G) ?= e(\pi _h, G \cdot Z(t))\)Where \(\pi _h= G \cdot H(t)\). If the connection between this equation and \(A \cdot B - C = H \cdot Z\) does not make sense to you, go back and read the article on pairings.We saw above how to convert \(A, B\) and \(C\) into elliptic curve points; \(G\) is just the generator (ie. the elliptic curve point equivalent of the number one). We can add \(G \cdot Z(t)\) to the trusted setup. \(H\) is harder; \(H\) is just a polynomial, and we predict very little ahead of time about what its coefficients will be for each individual QAP solution. Hence, we need to add yet more data to the trusted setup; specifically the sequence:\(G, G \cdot t, G \cdot t^2, G \cdot t^3, G \cdot t^4 ...\).In the Zcash trusted setup, the sequence here goes up to about 2 million; this is how many powers of \(t\) you need to make sure that you will always be able to compute \(H(t)\), at least for the specific QAP instance that they care about. And with that, the prover can provide all of the information for the verifier to make the final check.There is one more detail that we need to discuss. Most of the time we don't just want to prove in the abstract that some solution exists for some specific problem; rather, we want to prove either the correctness of some specific solution (eg. proving that if you take the word "cow" and SHA3 hash it a million times, the final result starts with 0x73064fe5), or that a solution exists if you restrict some of the parameters. For example, in a cryptocurrency instantiation where transaction amounts and account balances are encrypted, you want to prove that you know some decryption key k such that:decrypt(old_balance, k) >= decrypt(tx_value, k) decrypt(old_balance, k) - decrypt(tx_value, k) = decrypt(new_balance, k) The encrypted old_balance, tx_value and new_balance should be specified publicly, as those are the specific values that we are looking to verify at that particular time; only the decryption key should be hidden. Some slight modifications to the protocol are needed to create a "custom verification key" that corresponds to some specific restriction on the inputs.Now, let's step back a bit. First of all, here's the verification algorithm in its entirety, courtesy of ben Sasson, Tromer, Virza and Chiesa:The first line deals with parametrization; essentially, you can think of its function as being to create a "custom verification key" for the specific instance of the problem where some of the arguments are specified. The second line is the linear combination check for \(A, B\) and \(C\); the third line is the check that the linear combinations have the same coefficients, and the fourth line is the product check \(A \cdot B - C = H \cdot Z\).Altogether, the verification process is a few elliptic curve multiplications (one for each "public" input variable), and five pairing checks, one of which includes an additional pairing multiplication. The proof contains eight elliptic curve points: a pair of points each for \(A(t), B(t)\) and \(C(t)\), a point \(\pi _k\) for \(b \cdot (A(t) + B(t) + C(t))\), and a point \(\pi _h\) for \(H(t)\). Seven of these points are on the \(F_p\) curve (32 bytes each, as you can compress the \(y\) coordinate to a single bit), and in the Zcash implementation one point (\(\pi _b\)) is on the twisted curve in \(F_\) (64 bytes), so the total size of the proof is ~288 bytes.The two computationally hardest parts of creating a proof are:Dividing \((A \cdot B - C) / Z\) to get \(H\) (algorithms based on the Fast Fourier transform can do this in sub-quadratic time, but it's still quite computationally intensive) Making the elliptic curve multiplications and additions to create the \(A(t), B(t), C(t)\) and \(H(t)\) values and their corresponding pairs The basic reason why creating a proof is so hard is the fact that what was a single binary logic gate in the original computation turns into an operation that must be cryptographically processed through elliptic curve operations if we are making a zero-knowledge proof out of it. This fact, together with the superlinearity of fast Fourier transforms, means that proof creation takes ~20–40 seconds for a Zcash transaction.Another very important question is: can we try to make the trusted setup a little... less trust-demanding? Unfortunately we can't make it completely trustless; the KoE assumption itself precludes making independent pairs \((P_i, P_i \cdot k)\) without knowing what \(k\) is. However, we can increase security greatly by using \(N\)-of-\(N\) multiparty computation - that is, constructing the trusted setup between \(N\) parties in such a way that as long as at least one of the participants deleted their toxic waste then you're okay.To get a bit of a feel for how you would do this, here's a simple algorithm for taking an existing set (\(G, G \cdot t, G \cdot t^2, G \cdot t^3...\)), and "adding in" your own secret so that you need both your secret and the previous secret (or previous set of secrets) to cheat.The output set is simply:\(G, (G \cdot t) \cdot s, (G \cdot t^2) \cdot s^2, (G \cdot t^3) \cdot s^3...\)Note that you can produce this set knowing only the original set and s, and the new set functions in the same way as the old set, except now using \(t \cdot s\) as the "toxic waste" instead of \(t\). As long as you and the person (or people) who created the previous set do not both fail to delete your toxic waste and later collude, the set is "safe".Doing this for the complete trusted setup is quite a bit harder, as there are several values involved, and the algorithm has to be done between the parties in several rounds. It's an area of active research to see if the multi-party computation algorithm can be simplified further and made to require fewer rounds or made more parallelizable, as the more you can do that the more parties it becomes feasible to include into the trusted setup procedure. It's reasonable to see why a trusted setup between six participants who all know and work with each other might make some people uncomfortable, but a trusted setup with thousands of participants would be nearly indistinguishable from no trust at all - and if you're really paranoid, you can get in and participate in the setup procedure yourself, and be sure that you personally deleted your value.Another area of active research is the use of other approaches that do not use pairings and the same trusted setup paradigm to achieve the same goal; see Eli ben Sasson's recent presentation for one alternative (though be warned, it's at least as mathematically complicated as SNARKs are!)Special thanks to Ariel Gabizon and Christian Reitwiessner for reviewing.
[Mirror] Zk-SNARKs: Under the Hood [Mirror] Zk-SNARKs: Under the Hood2017 Feb 01 See all posts [Mirror] Zk-SNARKs: Under the Hood This is a mirror of the post at https://medium.com/@VitalikButerin/zk-snarks-under-the-hood-b33151a013f6This is the third part of a series of articles explaining how the technology behind zk-SNARKs works; the previous articles on quadratic arithmetic programs and elliptic curve pairings are required reading, and this article will assume knowledge of both concepts. Basic knowledge of what zk-SNARKs are and what they do is also assumed. See also Christian Reitwiessner's article here for another technical introduction.In the previous articles, we introduced the quadratic arithmetic program, a way of representing any computational problem with a polynomial equation that is much more amenable to various forms of mathematical trickery. We also introduced elliptic curve pairings, which allow a very limited form of one-way homomorphic encryption that lets you do equality checking. Now, we are going to start from where we left off, and use elliptic curve pairings, together with a few other mathematical tricks, in order to allow a prover to prove that they know a solution for a particular QAP without revealing anything else about the actual solution.This article will focus on the Pinocchio protocol by Parno, Gentry, Howell and Raykova from 2013 (often called PGHR13); there are a few variations on the basic mechanism, so a zk-SNARK scheme implemented in practice may work slightly differently, but the basic principles will in general remain the same.To start off, let us go into the key cryptographic assumption underlying the security of the mechanism that we are going to use: the *knowledge-of-exponent* assumption.Basically, if you get a pair of points \(P\) and \(Q\), where \(P \cdot k = Q\), and you get a point \(C\), then it is not possible to come up with \(C \cdot k\) unless \(C\) is "derived" from \(P\) in some way that you know. This may seem intuitively obvious, but this assumption actually cannot be derived from any other assumption (eg. discrete log hardness) that we usually use when proving security of elliptic curve-based protocols, and so zk-SNARKs do in fact rest on a somewhat shakier foundation than elliptic curve cryptography more generally — although it's still sturdy enough that most cryptographers are okay with it.Now, let's go into how this can be used. Supposed that a pair of points \((P, Q)\) falls from the sky, where \(P \cdot k = Q\), but nobody knows what the value of \(k\) is. Now, suppose that I come up with a pair of points \((R, S)\) where \(R \cdot k = S\). Then, the KoE assumption implies that the only way I could have made that pair of points was by taking \(P\) and \(Q\), and multiplying both by some factor r that I personally know. Note also that thanks to the magic of elliptic curve pairings, checking that \(R = k \cdot S\) doesn't actually require knowing \(k\) - instead, you can simply check whether or not \(e(R, Q) = e(P, S)\).Let's do something more interesting. Suppose that we have ten pairs of points fall from the sky: \((P_1, Q_1), (P_2, Q_2)... (P_, Q_)\). In all cases, \(P_i \cdot k = Q_i\). Suppose that I then provide you with a pair of points \((R, S)\) where \(R \cdot k = S\). What do you know now? You know that \(R\) is some linear combination \(P_1 \cdot i_1 + P_2 \cdot i_2 + ... + P_ \cdot i_\), where I know the coefficients \(i_1, i_2 ... i_\). That is, the only way to arrive at such a pair of points \((R, S)\) is to take some multiples of \(P_1, P_2 ... P_\) and add them together, and make the same calculation with \(Q_1, Q_2 ... Q_\).Note that, given any specific set of \(P_1...P_\) points that you might want to check linear combinations for, you can't actually create the accompanying \(Q_1...Q_\) points without knowing what \(k\) is, and if you do know what \(k\) is then you can create a pair \((R, S)\) where \(R \cdot k = S\) for whatever \(R\) you want, without bothering to create a linear combination. Hence, for this to work it's absolutely imperative that whoever creates those points is trustworthy and actually deletes \(k\) once they created the ten points. This is where the concept of a "trusted setup" comes from.Remember that the solution to a QAP is a set of polynomials \((A, B, C)\) such that \(A(x) \cdot B(x) - C(x) = H(x) \cdot Z(x)\), where:\(A\) is a linear combination of a set of polynomials \(\\) \(B\) is the linear combination of \(\\) with the same coefficients \(C\) is a linear combination of \(\\) with the same coefficients The sets \(\, \\) and \(\\) and the polynomial \(Z\) are part of the problem statement.However, in most real-world cases, \(A, B\) and \(C\) are extremely large; for something with many thousands of circuit gates like a hash function, the polynomials (and the factors for the linear combinations) may have many thousands of terms. Hence, instead of having the prover provide the linear combinations directly, we are going to use the trick that we introduced above to have the prover prove that they are providing something which is a linear combination, but without revealing anything else.You might have noticed that the trick above works on elliptic curve points, not polynomials. Hence, what actually happens is that we add the following values to the trusted setup:\(G \cdot A_1(t), G \cdot A_1(t) \cdot k_a\) \(G \cdot A_2(t), G \cdot A_2(t) \cdot k_a\) ... \(G \cdot B_1(t), G \cdot B_1(t) \cdot k_b\) \(G \cdot B_2(t), G \cdot B_2(t) \cdot k_b\) ... \(G \cdot C_1(t), G \cdot C_1(t) \cdot k_c\) \(G \cdot C_2(t), G \cdot C_2(t) \cdot k_c\) ... You can think of t as a "secret point" at which the polynomial is evaluated. \(G\) is a "generator" (some random elliptic curve point that is specified as part of the protocol) and \(t, k_a, k_b\) and \(k_c\) are "toxic waste", numbers that absolutely must be deleted at all costs, or else whoever has them will be able to make fake proofs. Now, if someone gives you a pair of points \(P\), \(Q\) such that \(P \cdot k_a = Q\) (reminder: we don't need \(k_a\) to check this, as we can do a pairing check), then you know that what they are giving you is a linear combination of \(A_i\) polynomials evaluated at \(t\).Hence, so far the prover must give:\(\pi _a = G \cdot A(t), \pi '_a = G \cdot A(t) \cdot k_a\) \(\pi _b = G \cdot B(t), \pi '_b = G \cdot B(t) \cdot k_b\) \(\pi _c = G \cdot C(t), \pi '_c = G \cdot C(t) \cdot k_c\) Note that the prover doesn't actually need to know (and shouldn't know!) \(t, k_a, k_b\) or \(k_c\) to compute these values; rather, the prover should be able to compute these values just from the points that we're adding to the trusted setup.The next step is to make sure that all three linear combinations have the same coefficients. This we can do by adding another set of values to the trusted setup: \(G \cdot (A_i(t) + B_i(t) + C_i(t)) \cdot b\), where \(b\) is another number that should be considered "toxic waste" and discarded as soon as the trusted setup is completed. We can then have the prover create a linear combination with these values with the same coefficients, and use the same pairing trick as above to verify that this value matches up with the provided \(A + B + C\).Finally, we need to prove that \(A \cdot B - C = H \cdot Z\). We do this once again with a pairing check:\(e(\pi _a, \pi _b) / e(\pi _c, G) ?= e(\pi _h, G \cdot Z(t))\)Where \(\pi _h= G \cdot H(t)\). If the connection between this equation and \(A \cdot B - C = H \cdot Z\) does not make sense to you, go back and read the article on pairings.We saw above how to convert \(A, B\) and \(C\) into elliptic curve points; \(G\) is just the generator (ie. the elliptic curve point equivalent of the number one). We can add \(G \cdot Z(t)\) to the trusted setup. \(H\) is harder; \(H\) is just a polynomial, and we predict very little ahead of time about what its coefficients will be for each individual QAP solution. Hence, we need to add yet more data to the trusted setup; specifically the sequence:\(G, G \cdot t, G \cdot t^2, G \cdot t^3, G \cdot t^4 ...\).In the Zcash trusted setup, the sequence here goes up to about 2 million; this is how many powers of \(t\) you need to make sure that you will always be able to compute \(H(t)\), at least for the specific QAP instance that they care about. And with that, the prover can provide all of the information for the verifier to make the final check.There is one more detail that we need to discuss. Most of the time we don't just want to prove in the abstract that some solution exists for some specific problem; rather, we want to prove either the correctness of some specific solution (eg. proving that if you take the word "cow" and SHA3 hash it a million times, the final result starts with 0x73064fe5), or that a solution exists if you restrict some of the parameters. For example, in a cryptocurrency instantiation where transaction amounts and account balances are encrypted, you want to prove that you know some decryption key k such that:decrypt(old_balance, k) >= decrypt(tx_value, k) decrypt(old_balance, k) - decrypt(tx_value, k) = decrypt(new_balance, k) The encrypted old_balance, tx_value and new_balance should be specified publicly, as those are the specific values that we are looking to verify at that particular time; only the decryption key should be hidden. Some slight modifications to the protocol are needed to create a "custom verification key" that corresponds to some specific restriction on the inputs.Now, let's step back a bit. First of all, here's the verification algorithm in its entirety, courtesy of ben Sasson, Tromer, Virza and Chiesa:The first line deals with parametrization; essentially, you can think of its function as being to create a "custom verification key" for the specific instance of the problem where some of the arguments are specified. The second line is the linear combination check for \(A, B\) and \(C\); the third line is the check that the linear combinations have the same coefficients, and the fourth line is the product check \(A \cdot B - C = H \cdot Z\).Altogether, the verification process is a few elliptic curve multiplications (one for each "public" input variable), and five pairing checks, one of which includes an additional pairing multiplication. The proof contains eight elliptic curve points: a pair of points each for \(A(t), B(t)\) and \(C(t)\), a point \(\pi _k\) for \(b \cdot (A(t) + B(t) + C(t))\), and a point \(\pi _h\) for \(H(t)\). Seven of these points are on the \(F_p\) curve (32 bytes each, as you can compress the \(y\) coordinate to a single bit), and in the Zcash implementation one point (\(\pi _b\)) is on the twisted curve in \(F_\) (64 bytes), so the total size of the proof is ~288 bytes.The two computationally hardest parts of creating a proof are:Dividing \((A \cdot B - C) / Z\) to get \(H\) (algorithms based on the Fast Fourier transform can do this in sub-quadratic time, but it's still quite computationally intensive) Making the elliptic curve multiplications and additions to create the \(A(t), B(t), C(t)\) and \(H(t)\) values and their corresponding pairs The basic reason why creating a proof is so hard is the fact that what was a single binary logic gate in the original computation turns into an operation that must be cryptographically processed through elliptic curve operations if we are making a zero-knowledge proof out of it. This fact, together with the superlinearity of fast Fourier transforms, means that proof creation takes ~20–40 seconds for a Zcash transaction.Another very important question is: can we try to make the trusted setup a little... less trust-demanding? Unfortunately we can't make it completely trustless; the KoE assumption itself precludes making independent pairs \((P_i, P_i \cdot k)\) without knowing what \(k\) is. However, we can increase security greatly by using \(N\)-of-\(N\) multiparty computation - that is, constructing the trusted setup between \(N\) parties in such a way that as long as at least one of the participants deleted their toxic waste then you're okay.To get a bit of a feel for how you would do this, here's a simple algorithm for taking an existing set (\(G, G \cdot t, G \cdot t^2, G \cdot t^3...\)), and "adding in" your own secret so that you need both your secret and the previous secret (or previous set of secrets) to cheat.The output set is simply:\(G, (G \cdot t) \cdot s, (G \cdot t^2) \cdot s^2, (G \cdot t^3) \cdot s^3...\)Note that you can produce this set knowing only the original set and s, and the new set functions in the same way as the old set, except now using \(t \cdot s\) as the "toxic waste" instead of \(t\). As long as you and the person (or people) who created the previous set do not both fail to delete your toxic waste and later collude, the set is "safe".Doing this for the complete trusted setup is quite a bit harder, as there are several values involved, and the algorithm has to be done between the parties in several rounds. It's an area of active research to see if the multi-party computation algorithm can be simplified further and made to require fewer rounds or made more parallelizable, as the more you can do that the more parties it becomes feasible to include into the trusted setup procedure. It's reasonable to see why a trusted setup between six participants who all know and work with each other might make some people uncomfortable, but a trusted setup with thousands of participants would be nearly indistinguishable from no trust at all - and if you're really paranoid, you can get in and participate in the setup procedure yourself, and be sure that you personally deleted your value.Another area of active research is the use of other approaches that do not use pairings and the same trusted setup paradigm to achieve the same goal; see Eli ben Sasson's recent presentation for one alternative (though be warned, it's at least as mathematically complicated as SNARKs are!)Special thanks to Ariel Gabizon and Christian Reitwiessner for reviewing. -
![[Mirror] Exploring Elliptic Curve Pairings](https://fastly.jsdelivr.net/npm/typecho-joe-next@6.0.0/assets/img/lazyload.jpg) [Mirror] Exploring Elliptic Curve Pairings [Mirror] Exploring Elliptic Curve Pairings2017 Jan 14 See all posts [Mirror] Exploring Elliptic Curve Pairings This is a mirror of the post at https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627Trigger warning: math.One of the key cryptographic primitives behind various constructions, including deterministic threshold signatures, zk-SNARKs and other simpler forms of zero-knowledge proofs is the elliptic curve pairing. Elliptic curve pairings (or "bilinear maps") are a recent addition to a 30-year-long history of using elliptic curves for cryptographic applications including encryption and digital signatures; pairings introduce a form of "encrypted multiplication", greatly expanding what elliptic curve-based protocols can do. The purpose of this article will be to go into elliptic curve pairings in detail, and explain a general outline of how they work.You're not expected to understand everything here the first time you read it, or even the tenth time; this stuff is genuinely hard. But hopefully this article will give you at least a bit of an idea as to what is going on under the hood.Elliptic curves themselves are very much a nontrivial topic to understand, and this article will generally assume that you know how they work; if you do not, I recommend this article here as a primer: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. As a quick summary, elliptic curve cryptography involves mathematical objects called "points" (these are literal two-dimensional points with \((x, y)\) coordinates), with special formulas for adding and subtracting them (ie. for calculating the coordinates of \(R = P + Q\)), and you can also multiply a point by an integer (ie. \(P \cdot n = P + P + ... + P\), though there's a much faster way to compute it if \(n\) is big). Here's how point addition looks like graphically.There exists a special point called the "point at infinity" (\(O\)), the equivalent of zero in point arithmetic; it's always the case that \(P + O = P\). Also, a curve has an "order"; there exists a number \(n\) such that \(P \cdot n = O\) for any \(P\) (and of course, \(P \cdot (n+1) = P, P \cdot (7 \cdot n + 5) = P \cdot 5\), and so on). There is also some commonly agreed upon "generator point" \(G\), which is understood to in some sense represent the number \(1\). Theoretically, any point on a curve (except \(O\)) can be \(G\); all that matters is that \(G\) is standardized.Pairings go a step further in that they allow you to check certain kinds of more complicated equations on elliptic curve points — for example, if \(P = G \cdot p, Q = G \cdot q\) and \(R = G \cdot r\), you can check whether or not \(p \cdot q = r\), having just \(P, Q\) and \(R\) as inputs. This might seem like the fundamental security guarantees of elliptic curves are being broken, as information about \(p\) is leaking from just knowing P, but it turns out that the leakage is highly contained — specifically, the decisional Diffie Hellman problem is easy, but the computational Diffie Hellman problem (knowing \(P\) and \(Q\) in the above example, computing \(R = G \cdot p \cdot q\)) and the discrete logarithm problem (recovering \(p\) from \(P\)) remain computationally infeasible (at least, if they were before).A third way to look at what pairings do, and one that is perhaps most illuminating for most of the use cases that we are about, is that if you view elliptic curve points as one-way encrypted numbers (that is, \(encrypt(p) = p \cdot G = P\)), then whereas traditional elliptic curve math lets you check linear constraints on the numbers (eg. if \(P = G \cdot p, Q = G \cdot q\) and \(R = G \cdot r\), checking \(5 \cdot P + 7 \cdot Q = 11 \cdot R\) is really checking that \(5 \cdot p + 7 \cdot q = 11 \cdot r\)), pairings let you check quadratic constraints (eg. checking \(e(P, Q) \cdot e(G, G \cdot 5) = 1\) is really checking that \(p \cdot q + 5 = 0\)). And going up to quadratic is enough to let us work with deterministic threshold signatures, quadratic arithmetic programs and all that other good stuff.Now, what is this funny \(e(P, Q)\) operator that we introduced above? This is the pairing. Mathematicians also sometimes call it a bilinear map; the word "bilinear" here basically means that it satisfies the constraints:\(e(P, Q + R) = e(P, Q) \cdot e(P, R)\)\(e(P + S, Q) = e(P, Q) \cdot e(S, Q)\)Note that \(+\) and \(\cdot\) can be arbitrary operators; when you're creating fancy new kinds of mathematical objects, abstract algebra doesn't care how \(+\) and \(\cdot\) are defined, as long as they are consistent in the usual ways, eg. \(a + b = b + a, (a \cdot b) \cdot c = a \cdot (b \cdot c)\) and \((a \cdot c) + (b \cdot c) = (a + b) \cdot c\).If \(P\), \(Q\), \(R\) and \(S\) were simple numbers, then making a simple pairing is easy: we can do \(e(x, y) = 2^\). Then, we can see:\(e(3, 4+ 5) = 2^ = 2^\)\(e(3, 4) \cdot e(3, 5) = 2^ \cdot 2^ = 2^ \cdot 2^ = 2^\)It's bilinear!However, such simple pairings are not suitable for cryptography because the objects that they work on are simple integers and are too easy to analyze; integers make it easy to divide, compute logarithms, and make various other computations; simple integers have no concept of a "public key" or a "one-way function". Additionally, with the pairing described above you can go backwards - knowing \(x\), and knowing \(e(x, y)\), you can simply compute a division and a logarithm to determine \(y\). We want mathematical objects that are as close as possible to "black boxes", where you can add, subtract, multiply and divide, but do nothing else. This is where elliptic curves and elliptic curve pairings come in.It turns out that it is possible to make a bilinear map over elliptic curve points — that is, come up with a function \(e(P, Q)\) where the inputs \(P\) and \(Q\) are elliptic curve points, and where the output is what's called an \((F_p)^\) element (at least in the specific case we will cover here; the specifics differ depending on the details of the curve, more on this later), but the math behind doing so is quite complex.First, let's cover prime fields and extension fields. The pretty elliptic curve in the picture earlier in this post only looks that way if you assume that the curve equation is defined using regular real numbers. However, if we actually use regular real numbers in cryptography, then you can use logarithms to "go backwards", and everything breaks; additionally, the amount of space needed to actually store and represent the numbers may grow arbitrarily. Hence, we instead use numbers in a prime field.A prime field consists of the set of numbers \(0, 1, 2... p-1\), where \(p\) is prime, and the various operations are defined as follows:\(a + b: (a + b)\) % \(p\)\(a \cdot b: (a \cdot b)\) % \(p\)\(a - b: (a - b)\) % \(p\)\(a / b: (a \cdot b^)\) % \(p\)Basically, all math is done modulo \(p\) (see here for an introduction to modular math). Division is a special case; normally, \(\frac\) is not an integer, and here we want to deal only with integers, so we instead try to find the number \(x\) such that \(x \cdot 2 = 3\), where \(\cdot\) of course refers to modular multiplication as defined above. Thanks to Fermat's little theorem, the exponentiation trick shown above does the job, but there is also a faster way to do it, using the Extended Euclidean Algorithm. Suppose \(p = 7\); here are a few examples:\(2 + 3 = 5\) % \(7 = 5\)\(4 + 6 = 10\) % \(7 = 3\)\(2 - 5 = -3\) % \(7 = 4\)\(6 \cdot 3 = 18\) % \(7 = 4\)\(3 / 2 = (3 \cdot 2^5)\) % \(7 = 5\)\(5 \cdot 2 = 10\) % \(7 = 3\)If you play around with this kind of math, you'll notice that it's perfectly consistent and satisfies all of the usual rules. The last two examples above show how \((a / b) \cdot b = a\); you can also see that \((a + b) + c = a + (b + c), (a + b) \cdot c = a \cdot c + b \cdot c\), and all the other high school algebraic identities you know and love continue to hold true as well. In elliptic curves in reality, the points and equations are usually computed in prime fields.Now, let's talk about extension fields. You have probably already seen an extension field before; the most common example that you encounter in math textbooks is the field of complex numbers, where the field of real numbers is "extended" with the additional element \(\sqrt = i\). Basically, extension fields work by taking an existing field, then "inventing" a new element and defining the relationship between that element and existing elements (in this case, \(i^2 + 1 = 0\)), making sure that this equation does not hold true for any number that is in the original field, and looking at the set of all linear combinations of elements of the original field and the new element that you have just created. We can do extensions of prime fields too; for example, we can extend the prime field \(\bmod 7\) that we described above with \(i\), and then we can do:\((2 + 3i) + (4 + 2i) = 6 + 5i\)\((5 + 2i) + 3 = 1 + 2i\)\((6 + 2i) \cdot 2 = 5 + 4i\)\(4i \cdot (2 + i) = 3 + i\)That last result may be a bit hard to figure out; what happened there was that we first decompose the product into \(4i \cdot 2 + 4i \cdot i\), which gives \(8i - 4\), and then because we are working in \(\bmod 7\) math that becomes \(i + 3\). To divide, we do:\(a / b: (a \cdot b^)\) % \(p\)Note that the exponent for Fermat's little theorem is now \(p^2\) instead of \(p\), though once again if we want to be more efficient we can also instead extend the Extended Euclidean Algorithm to do the job. Note that \(x^ = 1\) for any \(x\) in this field, so we call \(p^2 - 1\) the "order of the multiplicative group in the field".With real numbers, the Fundamental Theorem of Algebra ensures that the quadratic extension that we call the complex numbers is "complete" — you cannot extend it further, because for any mathematical relationship (at least, any mathematical relationship defined by an algebraic formula) that you can come up with between some new element \(j\) and the existing complex numbers, it's possible to come up with at least one complex number that already satisfies that relationship. With prime fields, however, we do not have this issue, and so we can go further and make cubic extensions (where the mathematical relationship between some new element \(w\) and existing field elements is a cubic equation, so \(1, w\) and \(w^2\) are all linearly independent of each other), higher-order extensions, extensions of extensions, etc. And it is these kinds of supercharged modular complex numbers that elliptic curve pairings are built on.For those interested in seeing the exact math involved in making all of these operations written out in code, prime fields and field extensions are implemented here: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.pyNow, on to elliptic curve pairings. An elliptic curve pairing (or rather, the specific form of pairing we'll explore here; there are also other types of pairings, though their logic is fairly similar) is a map \(G_2 \times G_1 \rightarrow G_t\), where:\(\bf G_1\) is an elliptic curve, where points satisfy an equation of the form \(y^2 = x^3 + b\), and where both coordinates are elements of \(F_p\) (ie. they are simple numbers, except arithmetic is all done modulo some prime number) \(\bf G_2\) is an elliptic curve, where points satisfy the same equation as \(G_1\), except where the coordinates are elements of \((F_p)^\) (ie. they are the supercharged complex numbers we talked about above; we define a new "magic number" \(w\), which is defined by a \(12\)th degree polynomial like \(w^ - 18 \cdot w^6 + 82 = 0\)) \(\bf G_t\) is the type of object that the result of the elliptic curve goes into. In the curves that we look at, \(G_t\) is \(\bf (F_p)^\) (the same supercharged complex number as used in \(G_2\)) The main property that it must satisfy is bilinearity, which in this context means that:\(e(P, Q + R) = e(P, Q) \cdot e(P, R)\) \(e(P + Q, R) = e(P, R) \cdot e(Q, R)\) There are two other important criteria:Efficient computability (eg. we can make an easy pairing by simply taking the discrete logarithms of all points and multiplying them together, but this is as computationally hard as breaking elliptic curve cryptography in the first place, so it doesn't count) Non-degeneracy (sure, you could just define \(e(P, Q) = 1\), but that's not a particularly useful pairing) So how do we do this?The math behind why pairing functions work is quite tricky and involves quite a bit of advanced algebra going even beyond what we've seen so far, but I'll provide an outline. First of all, we need to define the concept of a divisor, basically an alternative way of representing functions on elliptic curve points. A divisor of a function basically counts the zeroes and the infinities of the function. To see what this means, let's go through a few examples. Let us fix some point \(P = (P_x, P_y)\), and consider the following function:\(f(x, y) = x - P_x\)The divisor is \([P] + [-P] - 2 \cdot [O]\) (the square brackets are used to represent the fact that we are referring to the presence of the point \(P\) in the set of zeroes and infinities of the function, not the point P itself; \([P] + [Q]\) is not the same thing as \([P + Q]\)). The reasoning is as follows:The function is equal to zero at \(P\), since \(x\) is \(P_x\), so \(x - P_x = 0\) The function is equal to zero at \(-P\), since \(-P\) and \(P\) share the same \(x\) coordinate The function goes to infinity as \(x\) goes to infinity, so we say the function is equal to infinity at \(O\). There's a technical reason why this infinity needs to be counted twice, so \(O\) gets added with a "multiplicity" of \(-2\) (negative because it's an infinity and not a zero, two because of this double counting). The technical reason is roughly this: because the equation of the curve is \(x^3 = y^2 + b, y\) goes to infinity "\(1.5\) times faster" than \(x\) does in order for \(y^2\) to keep up with \(x^3\); hence, if a linear function includes only \(x\) then it is represented as an infinity of multiplicity \(2\), but if it includes \(y\) then it is represented as an infinity of multiplicity \(3\).Now, consider a "line function":\(ax + by + c = 0\)Where \(a\), \(b\) and \(c\) are carefully chosen so that the line passes through points \(P\) and \(Q\). Because of how elliptic curve addition works (see the diagram at the top), this also means that it passes through \(-P-Q\). And it goes up to infinity dependent on both \(x\) and \(y\), so the divisor becomes \([P]+ [Q] + [-P-Q] - 3 \cdot [O]\). We know that every "rational function" (ie. a function defined only using a finite number of \(+, -, \cdot\) and \(/\) operations on the coordinates of the point) uniquely corresponds to some divisor, up to multiplication by a constant (ie. if two functions \(F\) and \(G\) have the same divisor, then \(F = G \cdot k\) for some constant \(k\)).For any two functions \(F\) and \(G\), the divisor of \(F \cdot G\) is equal to the divisor of \(F\) plus the divisor of \(G\) (in math textbooks, you'll see \((F \cdot G) = (F) + (G)\)), so for example if \(f(x, y) = P_x - x\), then \((f^3) = 3 \cdot [P] + 3 \cdot [-P] - 6 \cdot [O]\); \(P\) and \(-P\) are "triple-counted" to account for the fact that \(f^3\) approaches \(0\) at those points "three times as quickly" in a certain mathematical sense.Note that there is a theorem that states that if you "remove the square brackets" from a divisor of a function, the points must add up to \(O ([P] + [Q] + [-P-Q] - 3 \cdot [O]\) clearly fits, as \(P + Q - P - Q - 3 \cdot O = O)\), and any divisor that has this property is the divisor of a function.Now, we're ready to look at Tate pairings. Consider the following functions, defined via their divisors:\((F_P) = n \cdot [P] - n \cdot [O]\), where \(n\) is the order of \(G_1\), ie. \(n \cdot P = O\) for any \(P\) \((F_Q) = n \cdot [Q] - n \cdot [O]\) \((g) = [P + Q] - [P] - [Q] + [O]\) Now, let's look at the product \(F_P \cdot F_Q \cdot g^n\). The divisor is:\(n \cdot [P] - n \cdot [O] + n \cdot [Q] - n \cdot [O] + n \cdot [P + Q] - n \cdot [P] - n \cdot [Q] + n \cdot [O]\)Which simplifies neatly to:\(n \cdot [P + Q] - n \cdot [O]\)Notice that this divisor is of exactly the same format as the divisor for \(F_P\) and \(F_Q\) above. Hence, \(F_P \cdot F_Q \cdot g^n = F_\).Now, we introduce a procedure called the "final exponentiation" step, where we take the result of our functions above (\(F_P, F_Q\), etc.) and raise it to the power \(z = (p^ - 1) / n\), where \(p^ - 1\) is the order of the multiplicative group in \((F_p)^\) (ie. for any \(x \in (F_p)^, x^ - 1)} = 1\)). Notice that if you apply this exponentiation to any result that has already been raised to the power of \(n\), you get an exponentiation to the power of \(p^ - 1\), so the result turns into \(1\). Hence, after final exponentiation, \(g^n\) cancels out and we get \(F_P^z \cdot F_Q^z = (F_)^z\). There's some bilinearity for you.Now, if you want to make a function that's bilinear in both arguments, you need to go into spookier math, where instead of taking \(F_P\) of a value directly, you take \(F_P\) of a divisor, and that's where the full "Tate pairing" comes from. To prove some more results you have to deal with notions like "linear equivalence" and "Weil reciprocity", and the rabbit hole goes on from there. You can find more reading material on all of this here and here.For an implementation of a modified version of the Tate pairing, called the optimal Ate paring, see here. The code implements Miller's algorithm, which is needed to actually compute \(F_P\).Note that the fact pairings like this are possible is somewhat of a mixed blessing: on the one hand, it means that all the protocols we can do with pairings become possible, but is also means that we have to be more careful about what elliptic curves we use.Every elliptic curve has a value called an embedding degree; essentially, the smallest \(k\) such that \(p^k - 1\) is a multiple of \(n\) (where \(p\) is the prime used for the field and \(n\) is the curve order). In the fields above, \(k = 12\), and in the fields used for traditional ECC (ie. where we don't care about pairings), the embedding degree is often extremely large, to the point that pairings are computationally infeasible to compute; however, if we are not careful then we can generate fields where \(k = 4\) or even \(1\).If \(k = 1\), then the "discrete logarithm" problem for elliptic curves (essentially, recovering \(p\) knowing only the point \(P = G \cdot p\), the problem that you have to solve to "crack" an elliptic curve private key) can be reduced into a similar math problem over \(F_p\), where the problem becomes much easier (this is called the MOV attack); using curves with an embedding degree of \(12\) or higher ensures that this reduction is either unavailable, or that solving the discrete log problem over pairing results is at least as hard as recovering a private key from a public key "the normal way" (ie. computationally infeasible). Do not worry; all standard curve parameters have been thoroughly checked for this issue.Stay tuned for a mathematical explanation of how zk-SNARKs work, coming soon.Special thanks to Christian Reitwiessner, Ariel Gabizon (from Zcash) and Alfred Menezes for reviewing and making corrections.
[Mirror] Exploring Elliptic Curve Pairings [Mirror] Exploring Elliptic Curve Pairings2017 Jan 14 See all posts [Mirror] Exploring Elliptic Curve Pairings This is a mirror of the post at https://medium.com/@VitalikButerin/exploring-elliptic-curve-pairings-c73c1864e627Trigger warning: math.One of the key cryptographic primitives behind various constructions, including deterministic threshold signatures, zk-SNARKs and other simpler forms of zero-knowledge proofs is the elliptic curve pairing. Elliptic curve pairings (or "bilinear maps") are a recent addition to a 30-year-long history of using elliptic curves for cryptographic applications including encryption and digital signatures; pairings introduce a form of "encrypted multiplication", greatly expanding what elliptic curve-based protocols can do. The purpose of this article will be to go into elliptic curve pairings in detail, and explain a general outline of how they work.You're not expected to understand everything here the first time you read it, or even the tenth time; this stuff is genuinely hard. But hopefully this article will give you at least a bit of an idea as to what is going on under the hood.Elliptic curves themselves are very much a nontrivial topic to understand, and this article will generally assume that you know how they work; if you do not, I recommend this article here as a primer: https://blog.cloudflare.com/a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/. As a quick summary, elliptic curve cryptography involves mathematical objects called "points" (these are literal two-dimensional points with \((x, y)\) coordinates), with special formulas for adding and subtracting them (ie. for calculating the coordinates of \(R = P + Q\)), and you can also multiply a point by an integer (ie. \(P \cdot n = P + P + ... + P\), though there's a much faster way to compute it if \(n\) is big). Here's how point addition looks like graphically.There exists a special point called the "point at infinity" (\(O\)), the equivalent of zero in point arithmetic; it's always the case that \(P + O = P\). Also, a curve has an "order"; there exists a number \(n\) such that \(P \cdot n = O\) for any \(P\) (and of course, \(P \cdot (n+1) = P, P \cdot (7 \cdot n + 5) = P \cdot 5\), and so on). There is also some commonly agreed upon "generator point" \(G\), which is understood to in some sense represent the number \(1\). Theoretically, any point on a curve (except \(O\)) can be \(G\); all that matters is that \(G\) is standardized.Pairings go a step further in that they allow you to check certain kinds of more complicated equations on elliptic curve points — for example, if \(P = G \cdot p, Q = G \cdot q\) and \(R = G \cdot r\), you can check whether or not \(p \cdot q = r\), having just \(P, Q\) and \(R\) as inputs. This might seem like the fundamental security guarantees of elliptic curves are being broken, as information about \(p\) is leaking from just knowing P, but it turns out that the leakage is highly contained — specifically, the decisional Diffie Hellman problem is easy, but the computational Diffie Hellman problem (knowing \(P\) and \(Q\) in the above example, computing \(R = G \cdot p \cdot q\)) and the discrete logarithm problem (recovering \(p\) from \(P\)) remain computationally infeasible (at least, if they were before).A third way to look at what pairings do, and one that is perhaps most illuminating for most of the use cases that we are about, is that if you view elliptic curve points as one-way encrypted numbers (that is, \(encrypt(p) = p \cdot G = P\)), then whereas traditional elliptic curve math lets you check linear constraints on the numbers (eg. if \(P = G \cdot p, Q = G \cdot q\) and \(R = G \cdot r\), checking \(5 \cdot P + 7 \cdot Q = 11 \cdot R\) is really checking that \(5 \cdot p + 7 \cdot q = 11 \cdot r\)), pairings let you check quadratic constraints (eg. checking \(e(P, Q) \cdot e(G, G \cdot 5) = 1\) is really checking that \(p \cdot q + 5 = 0\)). And going up to quadratic is enough to let us work with deterministic threshold signatures, quadratic arithmetic programs and all that other good stuff.Now, what is this funny \(e(P, Q)\) operator that we introduced above? This is the pairing. Mathematicians also sometimes call it a bilinear map; the word "bilinear" here basically means that it satisfies the constraints:\(e(P, Q + R) = e(P, Q) \cdot e(P, R)\)\(e(P + S, Q) = e(P, Q) \cdot e(S, Q)\)Note that \(+\) and \(\cdot\) can be arbitrary operators; when you're creating fancy new kinds of mathematical objects, abstract algebra doesn't care how \(+\) and \(\cdot\) are defined, as long as they are consistent in the usual ways, eg. \(a + b = b + a, (a \cdot b) \cdot c = a \cdot (b \cdot c)\) and \((a \cdot c) + (b \cdot c) = (a + b) \cdot c\).If \(P\), \(Q\), \(R\) and \(S\) were simple numbers, then making a simple pairing is easy: we can do \(e(x, y) = 2^\). Then, we can see:\(e(3, 4+ 5) = 2^ = 2^\)\(e(3, 4) \cdot e(3, 5) = 2^ \cdot 2^ = 2^ \cdot 2^ = 2^\)It's bilinear!However, such simple pairings are not suitable for cryptography because the objects that they work on are simple integers and are too easy to analyze; integers make it easy to divide, compute logarithms, and make various other computations; simple integers have no concept of a "public key" or a "one-way function". Additionally, with the pairing described above you can go backwards - knowing \(x\), and knowing \(e(x, y)\), you can simply compute a division and a logarithm to determine \(y\). We want mathematical objects that are as close as possible to "black boxes", where you can add, subtract, multiply and divide, but do nothing else. This is where elliptic curves and elliptic curve pairings come in.It turns out that it is possible to make a bilinear map over elliptic curve points — that is, come up with a function \(e(P, Q)\) where the inputs \(P\) and \(Q\) are elliptic curve points, and where the output is what's called an \((F_p)^\) element (at least in the specific case we will cover here; the specifics differ depending on the details of the curve, more on this later), but the math behind doing so is quite complex.First, let's cover prime fields and extension fields. The pretty elliptic curve in the picture earlier in this post only looks that way if you assume that the curve equation is defined using regular real numbers. However, if we actually use regular real numbers in cryptography, then you can use logarithms to "go backwards", and everything breaks; additionally, the amount of space needed to actually store and represent the numbers may grow arbitrarily. Hence, we instead use numbers in a prime field.A prime field consists of the set of numbers \(0, 1, 2... p-1\), where \(p\) is prime, and the various operations are defined as follows:\(a + b: (a + b)\) % \(p\)\(a \cdot b: (a \cdot b)\) % \(p\)\(a - b: (a - b)\) % \(p\)\(a / b: (a \cdot b^)\) % \(p\)Basically, all math is done modulo \(p\) (see here for an introduction to modular math). Division is a special case; normally, \(\frac\) is not an integer, and here we want to deal only with integers, so we instead try to find the number \(x\) such that \(x \cdot 2 = 3\), where \(\cdot\) of course refers to modular multiplication as defined above. Thanks to Fermat's little theorem, the exponentiation trick shown above does the job, but there is also a faster way to do it, using the Extended Euclidean Algorithm. Suppose \(p = 7\); here are a few examples:\(2 + 3 = 5\) % \(7 = 5\)\(4 + 6 = 10\) % \(7 = 3\)\(2 - 5 = -3\) % \(7 = 4\)\(6 \cdot 3 = 18\) % \(7 = 4\)\(3 / 2 = (3 \cdot 2^5)\) % \(7 = 5\)\(5 \cdot 2 = 10\) % \(7 = 3\)If you play around with this kind of math, you'll notice that it's perfectly consistent and satisfies all of the usual rules. The last two examples above show how \((a / b) \cdot b = a\); you can also see that \((a + b) + c = a + (b + c), (a + b) \cdot c = a \cdot c + b \cdot c\), and all the other high school algebraic identities you know and love continue to hold true as well. In elliptic curves in reality, the points and equations are usually computed in prime fields.Now, let's talk about extension fields. You have probably already seen an extension field before; the most common example that you encounter in math textbooks is the field of complex numbers, where the field of real numbers is "extended" with the additional element \(\sqrt = i\). Basically, extension fields work by taking an existing field, then "inventing" a new element and defining the relationship between that element and existing elements (in this case, \(i^2 + 1 = 0\)), making sure that this equation does not hold true for any number that is in the original field, and looking at the set of all linear combinations of elements of the original field and the new element that you have just created. We can do extensions of prime fields too; for example, we can extend the prime field \(\bmod 7\) that we described above with \(i\), and then we can do:\((2 + 3i) + (4 + 2i) = 6 + 5i\)\((5 + 2i) + 3 = 1 + 2i\)\((6 + 2i) \cdot 2 = 5 + 4i\)\(4i \cdot (2 + i) = 3 + i\)That last result may be a bit hard to figure out; what happened there was that we first decompose the product into \(4i \cdot 2 + 4i \cdot i\), which gives \(8i - 4\), and then because we are working in \(\bmod 7\) math that becomes \(i + 3\). To divide, we do:\(a / b: (a \cdot b^)\) % \(p\)Note that the exponent for Fermat's little theorem is now \(p^2\) instead of \(p\), though once again if we want to be more efficient we can also instead extend the Extended Euclidean Algorithm to do the job. Note that \(x^ = 1\) for any \(x\) in this field, so we call \(p^2 - 1\) the "order of the multiplicative group in the field".With real numbers, the Fundamental Theorem of Algebra ensures that the quadratic extension that we call the complex numbers is "complete" — you cannot extend it further, because for any mathematical relationship (at least, any mathematical relationship defined by an algebraic formula) that you can come up with between some new element \(j\) and the existing complex numbers, it's possible to come up with at least one complex number that already satisfies that relationship. With prime fields, however, we do not have this issue, and so we can go further and make cubic extensions (where the mathematical relationship between some new element \(w\) and existing field elements is a cubic equation, so \(1, w\) and \(w^2\) are all linearly independent of each other), higher-order extensions, extensions of extensions, etc. And it is these kinds of supercharged modular complex numbers that elliptic curve pairings are built on.For those interested in seeing the exact math involved in making all of these operations written out in code, prime fields and field extensions are implemented here: https://github.com/ethereum/py_pairing/blob/master/py_ecc/bn128/bn128_field_elements.pyNow, on to elliptic curve pairings. An elliptic curve pairing (or rather, the specific form of pairing we'll explore here; there are also other types of pairings, though their logic is fairly similar) is a map \(G_2 \times G_1 \rightarrow G_t\), where:\(\bf G_1\) is an elliptic curve, where points satisfy an equation of the form \(y^2 = x^3 + b\), and where both coordinates are elements of \(F_p\) (ie. they are simple numbers, except arithmetic is all done modulo some prime number) \(\bf G_2\) is an elliptic curve, where points satisfy the same equation as \(G_1\), except where the coordinates are elements of \((F_p)^\) (ie. they are the supercharged complex numbers we talked about above; we define a new "magic number" \(w\), which is defined by a \(12\)th degree polynomial like \(w^ - 18 \cdot w^6 + 82 = 0\)) \(\bf G_t\) is the type of object that the result of the elliptic curve goes into. In the curves that we look at, \(G_t\) is \(\bf (F_p)^\) (the same supercharged complex number as used in \(G_2\)) The main property that it must satisfy is bilinearity, which in this context means that:\(e(P, Q + R) = e(P, Q) \cdot e(P, R)\) \(e(P + Q, R) = e(P, R) \cdot e(Q, R)\) There are two other important criteria:Efficient computability (eg. we can make an easy pairing by simply taking the discrete logarithms of all points and multiplying them together, but this is as computationally hard as breaking elliptic curve cryptography in the first place, so it doesn't count) Non-degeneracy (sure, you could just define \(e(P, Q) = 1\), but that's not a particularly useful pairing) So how do we do this?The math behind why pairing functions work is quite tricky and involves quite a bit of advanced algebra going even beyond what we've seen so far, but I'll provide an outline. First of all, we need to define the concept of a divisor, basically an alternative way of representing functions on elliptic curve points. A divisor of a function basically counts the zeroes and the infinities of the function. To see what this means, let's go through a few examples. Let us fix some point \(P = (P_x, P_y)\), and consider the following function:\(f(x, y) = x - P_x\)The divisor is \([P] + [-P] - 2 \cdot [O]\) (the square brackets are used to represent the fact that we are referring to the presence of the point \(P\) in the set of zeroes and infinities of the function, not the point P itself; \([P] + [Q]\) is not the same thing as \([P + Q]\)). The reasoning is as follows:The function is equal to zero at \(P\), since \(x\) is \(P_x\), so \(x - P_x = 0\) The function is equal to zero at \(-P\), since \(-P\) and \(P\) share the same \(x\) coordinate The function goes to infinity as \(x\) goes to infinity, so we say the function is equal to infinity at \(O\). There's a technical reason why this infinity needs to be counted twice, so \(O\) gets added with a "multiplicity" of \(-2\) (negative because it's an infinity and not a zero, two because of this double counting). The technical reason is roughly this: because the equation of the curve is \(x^3 = y^2 + b, y\) goes to infinity "\(1.5\) times faster" than \(x\) does in order for \(y^2\) to keep up with \(x^3\); hence, if a linear function includes only \(x\) then it is represented as an infinity of multiplicity \(2\), but if it includes \(y\) then it is represented as an infinity of multiplicity \(3\).Now, consider a "line function":\(ax + by + c = 0\)Where \(a\), \(b\) and \(c\) are carefully chosen so that the line passes through points \(P\) and \(Q\). Because of how elliptic curve addition works (see the diagram at the top), this also means that it passes through \(-P-Q\). And it goes up to infinity dependent on both \(x\) and \(y\), so the divisor becomes \([P]+ [Q] + [-P-Q] - 3 \cdot [O]\). We know that every "rational function" (ie. a function defined only using a finite number of \(+, -, \cdot\) and \(/\) operations on the coordinates of the point) uniquely corresponds to some divisor, up to multiplication by a constant (ie. if two functions \(F\) and \(G\) have the same divisor, then \(F = G \cdot k\) for some constant \(k\)).For any two functions \(F\) and \(G\), the divisor of \(F \cdot G\) is equal to the divisor of \(F\) plus the divisor of \(G\) (in math textbooks, you'll see \((F \cdot G) = (F) + (G)\)), so for example if \(f(x, y) = P_x - x\), then \((f^3) = 3 \cdot [P] + 3 \cdot [-P] - 6 \cdot [O]\); \(P\) and \(-P\) are "triple-counted" to account for the fact that \(f^3\) approaches \(0\) at those points "three times as quickly" in a certain mathematical sense.Note that there is a theorem that states that if you "remove the square brackets" from a divisor of a function, the points must add up to \(O ([P] + [Q] + [-P-Q] - 3 \cdot [O]\) clearly fits, as \(P + Q - P - Q - 3 \cdot O = O)\), and any divisor that has this property is the divisor of a function.Now, we're ready to look at Tate pairings. Consider the following functions, defined via their divisors:\((F_P) = n \cdot [P] - n \cdot [O]\), where \(n\) is the order of \(G_1\), ie. \(n \cdot P = O\) for any \(P\) \((F_Q) = n \cdot [Q] - n \cdot [O]\) \((g) = [P + Q] - [P] - [Q] + [O]\) Now, let's look at the product \(F_P \cdot F_Q \cdot g^n\). The divisor is:\(n \cdot [P] - n \cdot [O] + n \cdot [Q] - n \cdot [O] + n \cdot [P + Q] - n \cdot [P] - n \cdot [Q] + n \cdot [O]\)Which simplifies neatly to:\(n \cdot [P + Q] - n \cdot [O]\)Notice that this divisor is of exactly the same format as the divisor for \(F_P\) and \(F_Q\) above. Hence, \(F_P \cdot F_Q \cdot g^n = F_\).Now, we introduce a procedure called the "final exponentiation" step, where we take the result of our functions above (\(F_P, F_Q\), etc.) and raise it to the power \(z = (p^ - 1) / n\), where \(p^ - 1\) is the order of the multiplicative group in \((F_p)^\) (ie. for any \(x \in (F_p)^, x^ - 1)} = 1\)). Notice that if you apply this exponentiation to any result that has already been raised to the power of \(n\), you get an exponentiation to the power of \(p^ - 1\), so the result turns into \(1\). Hence, after final exponentiation, \(g^n\) cancels out and we get \(F_P^z \cdot F_Q^z = (F_)^z\). There's some bilinearity for you.Now, if you want to make a function that's bilinear in both arguments, you need to go into spookier math, where instead of taking \(F_P\) of a value directly, you take \(F_P\) of a divisor, and that's where the full "Tate pairing" comes from. To prove some more results you have to deal with notions like "linear equivalence" and "Weil reciprocity", and the rabbit hole goes on from there. You can find more reading material on all of this here and here.For an implementation of a modified version of the Tate pairing, called the optimal Ate paring, see here. The code implements Miller's algorithm, which is needed to actually compute \(F_P\).Note that the fact pairings like this are possible is somewhat of a mixed blessing: on the one hand, it means that all the protocols we can do with pairings become possible, but is also means that we have to be more careful about what elliptic curves we use.Every elliptic curve has a value called an embedding degree; essentially, the smallest \(k\) such that \(p^k - 1\) is a multiple of \(n\) (where \(p\) is the prime used for the field and \(n\) is the curve order). In the fields above, \(k = 12\), and in the fields used for traditional ECC (ie. where we don't care about pairings), the embedding degree is often extremely large, to the point that pairings are computationally infeasible to compute; however, if we are not careful then we can generate fields where \(k = 4\) or even \(1\).If \(k = 1\), then the "discrete logarithm" problem for elliptic curves (essentially, recovering \(p\) knowing only the point \(P = G \cdot p\), the problem that you have to solve to "crack" an elliptic curve private key) can be reduced into a similar math problem over \(F_p\), where the problem becomes much easier (this is called the MOV attack); using curves with an embedding degree of \(12\) or higher ensures that this reduction is either unavailable, or that solving the discrete log problem over pairing results is at least as hard as recovering a private key from a public key "the normal way" (ie. computationally infeasible). Do not worry; all standard curve parameters have been thoroughly checked for this issue.Stay tuned for a mathematical explanation of how zk-SNARKs work, coming soon.Special thanks to Christian Reitwiessner, Ariel Gabizon (from Zcash) and Alfred Menezes for reviewing and making corrections. -
![[Mirror] Quadratic Arithmetic Programs: from Zero to Hero](https://fastly.jsdelivr.net/npm/typecho-joe-next@6.0.0/assets/img/lazyload.jpg) [Mirror] Quadratic Arithmetic Programs: from Zero to Hero [Mirror] Quadratic Arithmetic Programs: from Zero to Hero2016 Dec 10 See all posts [Mirror] Quadratic Arithmetic Programs: from Zero to Hero This is a mirror of the post at https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649There has been a lot of interest lately in the technology behind zk-SNARKs, and people are increasingly trying to demystify something that many have come to call "moon math" due to its perceived sheer indecipherable complexity. zk-SNARKs are indeed quite challenging to grasp, especially due to the sheer number of moving parts that need to come together for the whole thing to work, but if we break the technology down piece by piece then comprehending it becomes simpler.The purpose of this post is not to serve as a full introduction to zk-SNARKs; it assumes as background knowledge that (i) you know what zk-SNARKs are and what they do, and (ii) know enough math to be able to reason about things like polynomials (if the statement \(P(x) + Q(x) = (P + Q)(x)\) , where \(P\) and \(Q\) are polynomials, seems natural and obvious to you, then you're at the right level). Rather, the post digs deeper into the machinery behind the technology, and tries to explain as well as possible the first half of the pipeline, as drawn by zk-SNARK researcher Eran Tromer here:The steps here can be broken up into two halves. First, zk-SNARKs cannot be applied to any computational problem directly; rather, you have to convert the problem into the right "form" for the problem to operate on. The form is called a "quadratic arithmetic program" (QAP), and transforming the code of a function into one of these is itself highly nontrivial. Along with the process for converting the code of a function into a QAP is another process that can be run alongside so that if you have an input to the code you can create a corresponding solution (sometimes called "witness" to the QAP). After this, there is another fairly intricate process for creating the actual "zero knowledge proof" for this witness, and a separate process for verifying a proof that someone else passes along to you, but these are details that are out of scope for this post.The example that we will choose is a simple one: proving that you know the solution to a cubic equation: \(x^3 + x + 5 = 35\) (hint: the answer is \(3\)). This problem is simple enough that the resulting QAP will not be so large as to be intimidating, but nontrivial enough that you can see all of the machinery come into play.Let us write out our function as follows:def qeval(x): y = x**3 return x + y + 5The simple special-purpose programming language that we are using here supports basic arithmetic (\(+\), \(-\), \(\cdot\), \(/\)), constant-power exponentiation (\(x^7\) but not \(x^y\)) and variable assignment, which is powerful enough that you can theoretically do any computation inside of it (as long as the number of computational steps is bounded; no loops allowed). Note that modulo (%) and comparison operators (\(\), \(\leq\), \(\geq\)) are NOT supported, as there is no efficient way to do modulo or comparison directly in finite cyclic group arithmetic (be thankful for this; if there was a way to do either one, then elliptic curve cryptography would be broken faster than you can say "binary search" and "Chinese remainder theorem").You can extend the language to modulo and comparisons by providing bit decompositions (eg. \(13 = 2^3 + 2^2 + 1\)) as auxiliary inputs, proving correctness of those decompositions and doing the math in binary circuits; in finite field arithmetic, doing equality (==) checks is also doable and in fact a bit easier, but these are both details we won't get into right now. We can extend the language to support conditionals (eg. if \(x < 5: y = 7;\) else: \(y = 9\)) by converting them to an arithmetic form: \(y = 7 \cdot (x < 5) + 9 \cdot (x \geq 5)\) though note that both "paths" of the conditional would need to be executed, and if you have many nested conditionals then this can lead to a large amount of overhead.Let us now go through this process step by step. If you want to do this yourself for any piece of code, I implemented a compiler here (for educational purposes only; not ready for making QAPs for real-world zk-SNARKs quite yet!).FlatteningThe first step is a "flattening" procedure, where we convert the original code, which may contain arbitrarily complex statements and expressions, into a sequence of statements that are of two forms: \(x = y\) (where \(y\) can be a variable or a number) and \(x = y\) \((op)\) \(z\) (where \(op\) can be \(+\), \(-\), \(\cdot\), \(/\) and \(y\) and \(z\) can be variables, numbers or themselves sub-expressions). You can think of each of these statements as being kind of like logic gates in a circuit. The result of the flattening process for the above code is as follows:sym_1 = x * x y = sym_1 * x sym_2 = y + x ~out = sym_2 + 5If you read the original code and the code here, you can fairly easily see that the two are equivalent.Gates to R1CSNow, we convert this into something called a rank-1 constraint system (R1CS). An R1CS is a sequence of groups of three vectors (\(a\), \(b\), \(c\)), and the solution to an R1CS is a vector \(s\), where \(s\) must satisfy the equation \(s . a \cdot s . b - s . c = 0\), where \(.\) represents the dot product - in simpler terms, if we "zip together" \(a\) and \(s\), multiplying the two values in the same positions, and then take the sum of these products, then do the same to \(b\) and \(s\) and then \(c\) and \(s\), then the third result equals the product of the first two results. For example, this is a satisfied R1CS: But instead of having just one constraint, we are going to have many constraints: one for each logic gate. There is a standard way of converting a logic gate into a \((a, b, c)\) triple depending on what the operation is (\(+\), \(-\), \(\cdot\) or \(/\)) and whether the arguments are variables or numbers. The length of each vector is equal to the total number of variables in the system, including a dummy variable ~one at the first index representing the number \(1\), the input variables, a dummy variable ~out representing the output, and then all of the intermediate variables (\(sym_1\) and \(sym_2\) above); the vectors are generally going to be very sparse, only filling in the slots corresponding to the variables that are affected by some particular logic gate.First, we'll provide the variable mapping that we'll use:'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'The solution vector will consist of assignments for all of these variables, in that order.Now, we'll give the \((a, b, c)\) triple for the first gate:a = [0, 1, 0, 0, 0, 0] b = [0, 1, 0, 0, 0, 0] c = [0, 0, 0, 1, 0, 0]You can see that if the solution vector contains \(3\) in the second position, and \(9\) in the fourth position, then regardless of the rest of the contents of the solution vector, the dot product check will boil down to \(3 \cdot 3 = 9\), and so it will pass. If the solution vector has \(-3\) in the second position and \(9\) in the fourth position, the check will also pass; in fact, if the solution vector has \(7\) in the second position and \(49\) in the fourth position then that check will still pass — the purpose of this first check is to verify the consistency of the inputs and outputs of the first gate only.Now, let's go on to the second gate:a = [0, 0, 0, 1, 0, 0] b = [0, 1, 0, 0, 0, 0] c = [0, 0, 0, 0, 1, 0]In a similar style to the first dot product check, here we're checking that \(sym_1 \cdot x = y\).Now, the third gate:a = [0, 1, 0, 0, 1, 0] b = [1, 0, 0, 0, 0, 0] c = [0, 0, 0, 0, 0, 1]Here, the pattern is somewhat different: it's multiplying the first element in the solution vector by the second element, then by the fifth element, adding the two results, and checking if the sum equals the sixth element. Because the first element in the solution vector is always one, this is just an addition check, checking that the output equals the sum of the two inputs.Finally, the fourth gate:a = [5, 0, 0, 0, 0, 1] b = [1, 0, 0, 0, 0, 0] c = [0, 0, 1, 0, 0, 0]Here, we're evaluating the last check, ~out \(= sym_2 + 5\). The dot product check works by taking the sixth element in the solution vector, adding five times the first element (reminder: the first element is \(1\), so this effectively means adding \(5\)), and checking it against the third element, which is where we store the output variable.And there we have our R1CS with four constraints. The witness is simply the assignment to all the variables, including input, output and internal variables:[1, 3, 35, 9, 27, 30]You can compute this for yourself by simply "executing" the flattened code above, starting off with the input variable assignment \(x=3\), and putting in the values of all the intermediate variables and the output as you compute them.The complete R1CS put together is:A [0, 1, 0, 0, 0, 0] [0, 0, 0, 1, 0, 0] [0, 1, 0, 0, 1, 0] [5, 0, 0, 0, 0, 1] B [0, 1, 0, 0, 0, 0] [0, 1, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0] C [0, 0, 0, 1, 0, 0] [0, 0, 0, 0, 1, 0] [0, 0, 0, 0, 0, 1] [0, 0, 1, 0, 0, 0]R1CS to QAPThe next step is taking this R1CS and converting it into QAP form, which implements the exact same logic except using polynomials instead of dot products. We do this as follows. We go 3from four groups of three vectors of length six to six groups of three degree-3 polynomials, where evaluating the polynomials at each x coordinate represents one of the constraints. That is, if we evaluate the polynomials at \(x=1\), then we get our first set of vectors, if we evaluate the polynomials at \(x=2\), then we get our second set of vectors, and so on.We can make this transformation using something called a Lagrange interpolation. The problem that a Lagrange interpolation solves is this: if you have a set of points (ie. \((x, y)\) coordinate pairs), then doing a Lagrange interpolation on those points gives you a polynomial that passes through all of those points. We do this by decomposing the problem: for each \(x\) coordinate, we create a polynomial that has the desired \(y\) coordinate at that \(x\) coordinate and a \(y\) coordinate of \(0\) at all the other \(x\) coordinates we are interested in, and then to get the final result we add all of the polynomials together.Let's do an example. Suppose that we want a polynomial that passes through \((1, 3), (2, 2)\) and \((3, 4)\). We start off by making a polynomial that passes through \((1, 3), (2, 0)\) and \((3, 0)\). As it turns out, making a polynomial that "sticks out" at \(x=1\) and is zero at the other points of interest is easy; we simply do:(x - 2) * (x - 3)Which looks like this: Now, we just need to "rescale" it so that the height at x=1 is right:(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))This gives us:1.5 * x**2 - 7.5 * x + 9 We then do the same with the other two points, and get two other similar-looking polynomials, except that they "stick out" at \(x=2\) and \(x=3\) instead of \(x=1\). We add all three together and get:1.5 * x**2 - 5.5 * x + 7 With exactly the coordinates that we want. The algorithm as described above takes \(O(n^3)\) time, as there are \(n\) points and each point requires \(O(n^2)\) time to multiply the polynomials together; with a little thinking, this can be reduced to \(O(n^2)\) time, and with a lot more thinking, using fast Fourier transform algorithms and the like, it can be reduced even further — a crucial optimization when functions that get used in zk-SNARKs in practice often have many thousands of gates.Now, let's use Lagrange interpolation to transform our R1CS. What we are going to do is take the first value out of every \(a\) vector, use Lagrange interpolation to make a polynomial out of that (where evaluating the polynomial at \(i\) gets you the first value of the \(i\)th \(a\) vector), repeat the process for the first value of every \(b\) and \(c\) vector, and then repeat that process for the second values, the third, values, and so on. For convenience I'll provide the answers right now:A polynomials [-5.0, 9.166, -5.0, 0.833] [8.0, -11.333, 5.0, -0.666] [0.0, 0.0, 0.0, 0.0] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5] [-1.0, 1.833, -1.0, 0.166] B polynomials [3.0, -5.166, 2.5, -0.333] [-2.0, 5.166, -2.5, 0.333] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] C polynomials [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [-1.0, 1.833, -1.0, 0.166] [4.0, -4.333, 1.5, -0.166] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5]Coefficients are in ascending order, so the first polynomial above is actually \(0.833 \cdot x^3 — 5 \cdot x^2 + 9.166 \cdot x - 5\). This set of polynomials (plus a Z polynomial that I will explain later) makes up the parameters for this particular QAP instance. Note that all of the work up until this point needs to be done only once for every function that you are trying to use zk-SNARKs to verify; once the QAP parameters are generated, they can be reused.Let's try evaluating all of these polynomials at \(x=1\). Evaluating a polynomial at \(x=1\) simply means adding up all the coefficients (as \(1^k = 1\) for all \(k\)), so it's not difficult. We get:A results at x=1 0 1 0 0 0 0 B results at x=1 0 1 0 0 0 0 C results at x=1 0 0 0 1 0 0And lo and behold, what we have here is exactly the same as the set of three vectors for the first logic gate that we created above.Checking the QAPNow what's the point of this crazy transformation? The answer is that instead of checking the constraints in the R1CS individually, we can now check all of the constraints at the same time by doing the dot product check on the polynomials. Because in this case the dot product check is a series of additions and multiplications of polynomials, the result is itself going to be a polynomial. If the resulting polynomial, evaluated at every \(x\) coordinate that we used above to represent a logic gate, is equal to zero, then that means that all of the checks pass; if the resulting polynomial evaluated at at least one of the \(x\) coordinate representing a logic gate gives a nonzero value, then that means that the values going into and out of that logic gate are inconsistent (ie. the gate is \(y = x \cdot sym_1\) but the provided values might be \(x = 2,sym_1 = 2\) and \(y = 5\)).Note that the resulting polynomial does not itself have to be zero, and in fact in most cases won't be; it could have any behavior at the points that don't correspond to any logic gates, as long as the result is zero at all the points that do correspond to some gate. To check correctness, we don't actually evaluate the polynomial \(t = A . s \cdot B . s - C . s\) at every point corresponding to a gate; instead, we divide \(t\) by another polynomial, \(Z\), and check that \(Z\) evenly divides \(t\) - that is, the division \(t / Z\) leaves no remainder.\(Z\) is defined as \((x - 1) \cdot (x - 2) \cdot (x - 3) ...\) - the simplest polynomial that is equal to zero at all points that correspond to logic gates. It is an elementary fact of algebra that any polynomial that is equal to zero at all of these points has to be a multiple of this minimal polynomial, and if a polynomial is a multiple of \(Z\) then its evaluation at any of those points will be zero; this equivalence makes our job much easier.Now, let's actually do the dot product check with the polynomials above. First, the intermediate polynomials:A . s = [43.0, -73.333, 38.5, -5.166] B . s = [-3.0, 10.333, -5.0, 0.666] C . s = [-41.0, 71.666, -24.5, 2.833]Now, \(A . s \cdot B . s — C . s\):t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Now, the minimal polynomial \(Z = (x - 1) \cdot (x - 2) \cdot (x - 3) \cdot (x - 4)\):Z = [24, -50, 35, -10, 1]And if we divide the result above by \(Z\), we get:h = t / Z = [-3.666, 17.055, -3.444]With no remainder.And so we have the solution for the QAP. If we try to falsify any of the variables in the R1CS solution that we are deriving this QAP solution from — say, set the last one to \(31\) instead of \(30\), then we get a \(t\) polynomial that fails one of the checks (in that particular case, the result at \(x=3\) would equal \(-1\) instead of \(0\)), and furthermore \(t\) would not be a multiple of \(Z\); rather, dividing \(t / Z\) would give a remainder of \([-5.0, 8.833, -4.5, 0.666]\).Note that the above is a simplification; "in the real world", the addition, multiplication, subtraction and division will happen not with regular numbers, but rather with finite field elements — a spooky kind of arithmetic which is self-consistent, so all the algebraic laws we know and love still hold true, but where all answers are elements of some finite-sized set, usually integers within the range from \(0\) to \(n-1\) for some \(n\). For example, if \(n = 13\), then \(1 / 2 = 7\) (and \(7 \cdot 2 = 1), 3 \cdot 5 = 2\), and so forth. Using finite field arithmetic removes the need to worry about rounding errors and allows the system to work nicely with elliptic curves, which end up being necessary for the rest of the zk-SNARK machinery that makes the zk-SNARK protocol actually secure.Special thanks to Eran Tromer for helping to explain many details about the inner workings of zk-SNARKs to me.
[Mirror] Quadratic Arithmetic Programs: from Zero to Hero [Mirror] Quadratic Arithmetic Programs: from Zero to Hero2016 Dec 10 See all posts [Mirror] Quadratic Arithmetic Programs: from Zero to Hero This is a mirror of the post at https://medium.com/@VitalikButerin/quadratic-arithmetic-programs-from-zero-to-hero-f6d558cea649There has been a lot of interest lately in the technology behind zk-SNARKs, and people are increasingly trying to demystify something that many have come to call "moon math" due to its perceived sheer indecipherable complexity. zk-SNARKs are indeed quite challenging to grasp, especially due to the sheer number of moving parts that need to come together for the whole thing to work, but if we break the technology down piece by piece then comprehending it becomes simpler.The purpose of this post is not to serve as a full introduction to zk-SNARKs; it assumes as background knowledge that (i) you know what zk-SNARKs are and what they do, and (ii) know enough math to be able to reason about things like polynomials (if the statement \(P(x) + Q(x) = (P + Q)(x)\) , where \(P\) and \(Q\) are polynomials, seems natural and obvious to you, then you're at the right level). Rather, the post digs deeper into the machinery behind the technology, and tries to explain as well as possible the first half of the pipeline, as drawn by zk-SNARK researcher Eran Tromer here:The steps here can be broken up into two halves. First, zk-SNARKs cannot be applied to any computational problem directly; rather, you have to convert the problem into the right "form" for the problem to operate on. The form is called a "quadratic arithmetic program" (QAP), and transforming the code of a function into one of these is itself highly nontrivial. Along with the process for converting the code of a function into a QAP is another process that can be run alongside so that if you have an input to the code you can create a corresponding solution (sometimes called "witness" to the QAP). After this, there is another fairly intricate process for creating the actual "zero knowledge proof" for this witness, and a separate process for verifying a proof that someone else passes along to you, but these are details that are out of scope for this post.The example that we will choose is a simple one: proving that you know the solution to a cubic equation: \(x^3 + x + 5 = 35\) (hint: the answer is \(3\)). This problem is simple enough that the resulting QAP will not be so large as to be intimidating, but nontrivial enough that you can see all of the machinery come into play.Let us write out our function as follows:def qeval(x): y = x**3 return x + y + 5The simple special-purpose programming language that we are using here supports basic arithmetic (\(+\), \(-\), \(\cdot\), \(/\)), constant-power exponentiation (\(x^7\) but not \(x^y\)) and variable assignment, which is powerful enough that you can theoretically do any computation inside of it (as long as the number of computational steps is bounded; no loops allowed). Note that modulo (%) and comparison operators (\(\), \(\leq\), \(\geq\)) are NOT supported, as there is no efficient way to do modulo or comparison directly in finite cyclic group arithmetic (be thankful for this; if there was a way to do either one, then elliptic curve cryptography would be broken faster than you can say "binary search" and "Chinese remainder theorem").You can extend the language to modulo and comparisons by providing bit decompositions (eg. \(13 = 2^3 + 2^2 + 1\)) as auxiliary inputs, proving correctness of those decompositions and doing the math in binary circuits; in finite field arithmetic, doing equality (==) checks is also doable and in fact a bit easier, but these are both details we won't get into right now. We can extend the language to support conditionals (eg. if \(x < 5: y = 7;\) else: \(y = 9\)) by converting them to an arithmetic form: \(y = 7 \cdot (x < 5) + 9 \cdot (x \geq 5)\) though note that both "paths" of the conditional would need to be executed, and if you have many nested conditionals then this can lead to a large amount of overhead.Let us now go through this process step by step. If you want to do this yourself for any piece of code, I implemented a compiler here (for educational purposes only; not ready for making QAPs for real-world zk-SNARKs quite yet!).FlatteningThe first step is a "flattening" procedure, where we convert the original code, which may contain arbitrarily complex statements and expressions, into a sequence of statements that are of two forms: \(x = y\) (where \(y\) can be a variable or a number) and \(x = y\) \((op)\) \(z\) (where \(op\) can be \(+\), \(-\), \(\cdot\), \(/\) and \(y\) and \(z\) can be variables, numbers or themselves sub-expressions). You can think of each of these statements as being kind of like logic gates in a circuit. The result of the flattening process for the above code is as follows:sym_1 = x * x y = sym_1 * x sym_2 = y + x ~out = sym_2 + 5If you read the original code and the code here, you can fairly easily see that the two are equivalent.Gates to R1CSNow, we convert this into something called a rank-1 constraint system (R1CS). An R1CS is a sequence of groups of three vectors (\(a\), \(b\), \(c\)), and the solution to an R1CS is a vector \(s\), where \(s\) must satisfy the equation \(s . a \cdot s . b - s . c = 0\), where \(.\) represents the dot product - in simpler terms, if we "zip together" \(a\) and \(s\), multiplying the two values in the same positions, and then take the sum of these products, then do the same to \(b\) and \(s\) and then \(c\) and \(s\), then the third result equals the product of the first two results. For example, this is a satisfied R1CS: But instead of having just one constraint, we are going to have many constraints: one for each logic gate. There is a standard way of converting a logic gate into a \((a, b, c)\) triple depending on what the operation is (\(+\), \(-\), \(\cdot\) or \(/\)) and whether the arguments are variables or numbers. The length of each vector is equal to the total number of variables in the system, including a dummy variable ~one at the first index representing the number \(1\), the input variables, a dummy variable ~out representing the output, and then all of the intermediate variables (\(sym_1\) and \(sym_2\) above); the vectors are generally going to be very sparse, only filling in the slots corresponding to the variables that are affected by some particular logic gate.First, we'll provide the variable mapping that we'll use:'~one', 'x', '~out', 'sym_1', 'y', 'sym_2'The solution vector will consist of assignments for all of these variables, in that order.Now, we'll give the \((a, b, c)\) triple for the first gate:a = [0, 1, 0, 0, 0, 0] b = [0, 1, 0, 0, 0, 0] c = [0, 0, 0, 1, 0, 0]You can see that if the solution vector contains \(3\) in the second position, and \(9\) in the fourth position, then regardless of the rest of the contents of the solution vector, the dot product check will boil down to \(3 \cdot 3 = 9\), and so it will pass. If the solution vector has \(-3\) in the second position and \(9\) in the fourth position, the check will also pass; in fact, if the solution vector has \(7\) in the second position and \(49\) in the fourth position then that check will still pass — the purpose of this first check is to verify the consistency of the inputs and outputs of the first gate only.Now, let's go on to the second gate:a = [0, 0, 0, 1, 0, 0] b = [0, 1, 0, 0, 0, 0] c = [0, 0, 0, 0, 1, 0]In a similar style to the first dot product check, here we're checking that \(sym_1 \cdot x = y\).Now, the third gate:a = [0, 1, 0, 0, 1, 0] b = [1, 0, 0, 0, 0, 0] c = [0, 0, 0, 0, 0, 1]Here, the pattern is somewhat different: it's multiplying the first element in the solution vector by the second element, then by the fifth element, adding the two results, and checking if the sum equals the sixth element. Because the first element in the solution vector is always one, this is just an addition check, checking that the output equals the sum of the two inputs.Finally, the fourth gate:a = [5, 0, 0, 0, 0, 1] b = [1, 0, 0, 0, 0, 0] c = [0, 0, 1, 0, 0, 0]Here, we're evaluating the last check, ~out \(= sym_2 + 5\). The dot product check works by taking the sixth element in the solution vector, adding five times the first element (reminder: the first element is \(1\), so this effectively means adding \(5\)), and checking it against the third element, which is where we store the output variable.And there we have our R1CS with four constraints. The witness is simply the assignment to all the variables, including input, output and internal variables:[1, 3, 35, 9, 27, 30]You can compute this for yourself by simply "executing" the flattened code above, starting off with the input variable assignment \(x=3\), and putting in the values of all the intermediate variables and the output as you compute them.The complete R1CS put together is:A [0, 1, 0, 0, 0, 0] [0, 0, 0, 1, 0, 0] [0, 1, 0, 0, 1, 0] [5, 0, 0, 0, 0, 1] B [0, 1, 0, 0, 0, 0] [0, 1, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0] [1, 0, 0, 0, 0, 0] C [0, 0, 0, 1, 0, 0] [0, 0, 0, 0, 1, 0] [0, 0, 0, 0, 0, 1] [0, 0, 1, 0, 0, 0]R1CS to QAPThe next step is taking this R1CS and converting it into QAP form, which implements the exact same logic except using polynomials instead of dot products. We do this as follows. We go 3from four groups of three vectors of length six to six groups of three degree-3 polynomials, where evaluating the polynomials at each x coordinate represents one of the constraints. That is, if we evaluate the polynomials at \(x=1\), then we get our first set of vectors, if we evaluate the polynomials at \(x=2\), then we get our second set of vectors, and so on.We can make this transformation using something called a Lagrange interpolation. The problem that a Lagrange interpolation solves is this: if you have a set of points (ie. \((x, y)\) coordinate pairs), then doing a Lagrange interpolation on those points gives you a polynomial that passes through all of those points. We do this by decomposing the problem: for each \(x\) coordinate, we create a polynomial that has the desired \(y\) coordinate at that \(x\) coordinate and a \(y\) coordinate of \(0\) at all the other \(x\) coordinates we are interested in, and then to get the final result we add all of the polynomials together.Let's do an example. Suppose that we want a polynomial that passes through \((1, 3), (2, 2)\) and \((3, 4)\). We start off by making a polynomial that passes through \((1, 3), (2, 0)\) and \((3, 0)\). As it turns out, making a polynomial that "sticks out" at \(x=1\) and is zero at the other points of interest is easy; we simply do:(x - 2) * (x - 3)Which looks like this: Now, we just need to "rescale" it so that the height at x=1 is right:(x - 2) * (x - 3) * 3 / ((1 - 2) * (1 - 3))This gives us:1.5 * x**2 - 7.5 * x + 9 We then do the same with the other two points, and get two other similar-looking polynomials, except that they "stick out" at \(x=2\) and \(x=3\) instead of \(x=1\). We add all three together and get:1.5 * x**2 - 5.5 * x + 7 With exactly the coordinates that we want. The algorithm as described above takes \(O(n^3)\) time, as there are \(n\) points and each point requires \(O(n^2)\) time to multiply the polynomials together; with a little thinking, this can be reduced to \(O(n^2)\) time, and with a lot more thinking, using fast Fourier transform algorithms and the like, it can be reduced even further — a crucial optimization when functions that get used in zk-SNARKs in practice often have many thousands of gates.Now, let's use Lagrange interpolation to transform our R1CS. What we are going to do is take the first value out of every \(a\) vector, use Lagrange interpolation to make a polynomial out of that (where evaluating the polynomial at \(i\) gets you the first value of the \(i\)th \(a\) vector), repeat the process for the first value of every \(b\) and \(c\) vector, and then repeat that process for the second values, the third, values, and so on. For convenience I'll provide the answers right now:A polynomials [-5.0, 9.166, -5.0, 0.833] [8.0, -11.333, 5.0, -0.666] [0.0, 0.0, 0.0, 0.0] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5] [-1.0, 1.833, -1.0, 0.166] B polynomials [3.0, -5.166, 2.5, -0.333] [-2.0, 5.166, -2.5, 0.333] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] C polynomials [0.0, 0.0, 0.0, 0.0] [0.0, 0.0, 0.0, 0.0] [-1.0, 1.833, -1.0, 0.166] [4.0, -4.333, 1.5, -0.166] [-6.0, 9.5, -4.0, 0.5] [4.0, -7.0, 3.5, -0.5]Coefficients are in ascending order, so the first polynomial above is actually \(0.833 \cdot x^3 — 5 \cdot x^2 + 9.166 \cdot x - 5\). This set of polynomials (plus a Z polynomial that I will explain later) makes up the parameters for this particular QAP instance. Note that all of the work up until this point needs to be done only once for every function that you are trying to use zk-SNARKs to verify; once the QAP parameters are generated, they can be reused.Let's try evaluating all of these polynomials at \(x=1\). Evaluating a polynomial at \(x=1\) simply means adding up all the coefficients (as \(1^k = 1\) for all \(k\)), so it's not difficult. We get:A results at x=1 0 1 0 0 0 0 B results at x=1 0 1 0 0 0 0 C results at x=1 0 0 0 1 0 0And lo and behold, what we have here is exactly the same as the set of three vectors for the first logic gate that we created above.Checking the QAPNow what's the point of this crazy transformation? The answer is that instead of checking the constraints in the R1CS individually, we can now check all of the constraints at the same time by doing the dot product check on the polynomials. Because in this case the dot product check is a series of additions and multiplications of polynomials, the result is itself going to be a polynomial. If the resulting polynomial, evaluated at every \(x\) coordinate that we used above to represent a logic gate, is equal to zero, then that means that all of the checks pass; if the resulting polynomial evaluated at at least one of the \(x\) coordinate representing a logic gate gives a nonzero value, then that means that the values going into and out of that logic gate are inconsistent (ie. the gate is \(y = x \cdot sym_1\) but the provided values might be \(x = 2,sym_1 = 2\) and \(y = 5\)).Note that the resulting polynomial does not itself have to be zero, and in fact in most cases won't be; it could have any behavior at the points that don't correspond to any logic gates, as long as the result is zero at all the points that do correspond to some gate. To check correctness, we don't actually evaluate the polynomial \(t = A . s \cdot B . s - C . s\) at every point corresponding to a gate; instead, we divide \(t\) by another polynomial, \(Z\), and check that \(Z\) evenly divides \(t\) - that is, the division \(t / Z\) leaves no remainder.\(Z\) is defined as \((x - 1) \cdot (x - 2) \cdot (x - 3) ...\) - the simplest polynomial that is equal to zero at all points that correspond to logic gates. It is an elementary fact of algebra that any polynomial that is equal to zero at all of these points has to be a multiple of this minimal polynomial, and if a polynomial is a multiple of \(Z\) then its evaluation at any of those points will be zero; this equivalence makes our job much easier.Now, let's actually do the dot product check with the polynomials above. First, the intermediate polynomials:A . s = [43.0, -73.333, 38.5, -5.166] B . s = [-3.0, 10.333, -5.0, 0.666] C . s = [-41.0, 71.666, -24.5, 2.833]Now, \(A . s \cdot B . s — C . s\):t = [-88.0, 592.666, -1063.777, 805.833, -294.777, 51.5, -3.444]Now, the minimal polynomial \(Z = (x - 1) \cdot (x - 2) \cdot (x - 3) \cdot (x - 4)\):Z = [24, -50, 35, -10, 1]And if we divide the result above by \(Z\), we get:h = t / Z = [-3.666, 17.055, -3.444]With no remainder.And so we have the solution for the QAP. If we try to falsify any of the variables in the R1CS solution that we are deriving this QAP solution from — say, set the last one to \(31\) instead of \(30\), then we get a \(t\) polynomial that fails one of the checks (in that particular case, the result at \(x=3\) would equal \(-1\) instead of \(0\)), and furthermore \(t\) would not be a multiple of \(Z\); rather, dividing \(t / Z\) would give a remainder of \([-5.0, 8.833, -4.5, 0.666]\).Note that the above is a simplification; "in the real world", the addition, multiplication, subtraction and division will happen not with regular numbers, but rather with finite field elements — a spooky kind of arithmetic which is self-consistent, so all the algebraic laws we know and love still hold true, but where all answers are elements of some finite-sized set, usually integers within the range from \(0\) to \(n-1\) for some \(n\). For example, if \(n = 13\), then \(1 / 2 = 7\) (and \(7 \cdot 2 = 1), 3 \cdot 5 = 2\), and so forth. Using finite field arithmetic removes the need to worry about rounding errors and allows the system to work nicely with elliptic curves, which end up being necessary for the rest of the zk-SNARK machinery that makes the zk-SNARK protocol actually secure.Special thanks to Eran Tromer for helping to explain many details about the inner workings of zk-SNARKs to me. -
![[Mirror] A Proof of Stake Design Philosophy](https://fastly.jsdelivr.net/npm/typecho-joe-next@6.0.0/assets/img/lazyload.jpg) [Mirror] A Proof of Stake Design Philosophy [Mirror] A Proof of Stake Design Philosophy2016 Dec 29 See all posts [Mirror] A Proof of Stake Design Philosophy This is a mirror of the post at https://medium.com/@VitalikButerin/a-proof-of-stake-design-philosophy-506585978d51Systems like Ethereum (and Bitcoin, and NXT, and Bitshares, etc) are a fundamentally new class of cryptoeconomic organisms — decentralized, jurisdictionless entities that exist entirely in cyberspace, maintained by a combination of cryptography, economics and social consensus. They are kind of like BitTorrent, but they are also not like BitTorrent, as BitTorrent has no concept of state — a distinction that turns out to be crucially important. They are sometimes described as decentralized autonomous corporations, but they are also not quite corporations — you can't hard fork Microsoft. They are kind of like open source software projects, but they are not quite that either — you can fork a blockchain, but not quite as easily as you can fork OpenOffice.These cryptoeconomic networks come in many flavors — ASIC-based PoW, GPU-based PoW, naive PoS, delegated PoS, hopefully soon Casper PoS — and each of these flavors inevitably comes with its own underlying philosophy. One well-known example is the maximalist vision of proof of work, where "the" correct blockchain, singular, is defined as the chain that miners have burned the largest amount of economic capital to create. Originally a mere in-protocol fork choice rule, this mechanism has in many cases been elevated to a sacred tenet — see this Twitter discussion between myself and Chris DeRose for an example of someone seriously trying to defend the idea in a pure form, even in the face of hash-algorithm-changing protocol hard forks. Bitshares' delegated proof of stake presents another coherent philosophy, where everything once again flows from a single tenet, but one that can be described even more simply: shareholders vote.Each of these philosophies; Nakamoto consensus, social consensus, shareholder voting consensus, leads to its own set of conclusions and leads to a system of values that makes quite a bit of sense when viewed on its own terms — though they can certainly be criticized when compared against each other. Casper consensus has a philosophical underpinning too, though one that has so far not been as succinctly articulated.Myself, Vlad, Dominic, Jae and others all have their own views on why proof of stake protocols exist and how to design them, but here I intend to explain where I personally am coming from.I'll proceed to listing observations and then conclusions directly.Cryptography is truly special in the 21st century because cryptography is one of the very few fields where adversarial conflict continues to heavily favor the defender. Castles are far easier to destroy than build, islands are defendable but can still be attacked, but an average person's ECC keys are secure enough to resist even state-level actors. Cypherpunk philosophy is fundamentally about leveraging this precious asymmetry to create a world that better preserves the autonomy of the individual, and cryptoeconomics is to some extent an extension of that, except this time protecting the safety and liveness of complex systems of coordination and collaboration, rather than simply the integrity and confidentiality of private messages. Systems that consider themselves ideological heirs to the cypherpunk spirit should maintain this basic property, and be much more expensive to destroy or disrupt than they are to use and maintain. The "cypherpunk spirit" isn't just about idealism; making systems that are easier to defend than they are to attack is also simply sound engineering. On medium to long time scales, humans are quite good at consensus. Even if an adversary had access to unlimited hashing power, and came out with a 51% attack of any major blockchain that reverted even the last month of history, convincing the community that this chain is legitimate is much harder than just outrunning the main chain's hashpower. They would need to subvert block explorers, every trusted member in the community, the New York Times, archive.org, and many other sources on the internet; all in all, convincing the world that the new attack chain is the one that came first in the information technology-dense 21st century is about as hard as convincing the world that the US moon landings never happened. These social considerations are what ultimately protect any blockchain in the long term, regardless of whether or not the blockchain's community admits it (note that Bitcoin Core does admit this primacy of the social layer). However, a blockchain protected by social consensus alone would be far too inefficient and slow, and too easy for disagreements to continue without end (though despite all difficulties, it has happened); hence, economic consensus serves an extremely important role in protecting liveness and safety properties in the short term. Because proof of work security can only come from block rewards (in Dominic Williams' terms, it lacks two of the three Es), and incentives to miners can only come from the risk of them losing their future block rewards, proof of work necessarily operates on a logic of massive power incentivized into existence by massive rewards. Recovery from attacks in PoW is very hard: the first time it happens, you can hard fork to change the PoW and thereby render the attacker's ASICs useless, but the second time you no longer have that option, and so the attacker can attack again and again. Hence, the size of the mining network has to be so large that attacks are inconceivable. Attackers of size less than X are discouraged from appearing by having the network constantly spend X every single day. I reject this logic because (i) it kills trees, and (ii) it fails to realize the cypherpunk spirit — cost of attack and cost of defense are at a 1:1 ratio, so there is no defender's advantage. Proof of stake breaks this symmetry by relying not on rewards for security, but rather penalties. Validators put money ("deposits") at stake, are rewarded slightly to compensate them for locking up their capital and maintaining nodes and taking extra precaution to ensure their private key safety, but the bulk of the cost of reverting transactions comes from penalties that are hundreds or thousands of times larger than the rewards that they got in the meantime. The "one-sentence philosophy" of proof of stake is thus not "security comes from burning energy", but rather "security comes from putting up economic value-at-loss". A given block or state has $X security if you can prove that achieving an equal level of finalization for any conflicting block or state cannot be accomplished unless malicious nodes complicit in an attempt to make the switch pay $X worth of in-protocol penalties. Theoretically, a majority collusion of validators may take over a proof of stake chain, and start acting maliciously. However, (i) through clever protocol design, their ability to earn extra profits through such manipulation can be limited as much as possible, and more importantly (ii) if they try to prevent new validators from joining, or execute 51% attacks, then the community can simply coordinate a hard fork and delete the offending validators' deposits. A successful attack may cost $50 million, but the process of cleaning up the consequences will not be that much more onerous than the geth/parity consensus failure of 2016.11.25. Two days later, the blockchain and community are back on track, attackers are $50 million poorer, and the rest of the community is likely richer since the attack will have caused the value of the token to go up due to the ensuing supply crunch. That's attack/defense asymmetry for you. The above should not be taken to mean that unscheduled hard forks will become a regular occurrence; if desired, the cost of a single 51% attack on proof of stake can certainly be set to be as high as the cost of a permanent 51% attack on proof of work, and the sheer cost and ineffectiveness of an attack should ensure that it is almost never attempted in practice. Economics is not everything. Individual actors may be motivated by extra-protocol motives, they may get hacked, they may get kidnapped, or they may simply get drunk and decide to wreck the blockchain one day and to hell with the cost. Furthermore, on the bright side, individuals' moral forbearances and communication inefficiencies will often raise the cost of an attack to levels much higher than the nominal protocol-defined value-at-loss. This is an advantage that we cannot rely on, but at the same time it is an advantage that we should not needlessly throw away. Hence, the best protocols are protocols that work well under a variety of models and assumptions— economic rationality with coordinated choice, economic rationality with individual choice, simple fault tolerance, Byzantine fault tolerance (ideally both the adaptive and non-adaptive adversary variants), Ariely/Kahneman-inspired behavioral economic models ("we all cheat just a little") and ideally any other model that's realistic and practical to reason about. It is important to have both layers of defense: economic incentives to discourage centralized cartels from acting anti-socially, and anti-centralization incentives to discourage cartels from forming in the first place. Consensus protocols that work as-fast-as-possible have risks and should be approached very carefully if at all, because if the possibility to be very fast is tied to incentives to do so, the combination will reward very high and systemic-risk-inducing levels of network-level centralization (eg. all validators running from the same hosting provider). Consensus protocols that don't care too much how fast a validator sends a message, as long as they do so within some acceptably long time interval (eg. 4–8 seconds, as we empirically know that latency in ethereum is usually ~500ms-1s) do not have these concerns. A possible middle ground is creating protocols that can work very quickly, but where mechanics similar to Ethereum's uncle mechanism ensure that the marginal reward for a node increasing its degree of network connectivity beyond some easily attainable point is fairly low. From here, there are of course many details and many ways to diverge on the details, but the above are the core principles that at least my version of Casper is based on. From here, we can certainly debate tradeoffs between competing values . Do we give ETH a 1% annual issuance rate and get an $50 million cost of forcing a remedial hard fork, or a zero annual issuance rate and get a $5 million cost of forcing a remedial hard fork? When do we increase a protocol's security under the economic model in exchange for decreasing its security under a fault tolerance model? Do we care more about having a predictable level of security or a predictable level of issuance? These are all questions for another post, and the various ways of implementing the different tradeoffs between these values are questions for yet more posts. But we'll get to it :)
[Mirror] A Proof of Stake Design Philosophy [Mirror] A Proof of Stake Design Philosophy2016 Dec 29 See all posts [Mirror] A Proof of Stake Design Philosophy This is a mirror of the post at https://medium.com/@VitalikButerin/a-proof-of-stake-design-philosophy-506585978d51Systems like Ethereum (and Bitcoin, and NXT, and Bitshares, etc) are a fundamentally new class of cryptoeconomic organisms — decentralized, jurisdictionless entities that exist entirely in cyberspace, maintained by a combination of cryptography, economics and social consensus. They are kind of like BitTorrent, but they are also not like BitTorrent, as BitTorrent has no concept of state — a distinction that turns out to be crucially important. They are sometimes described as decentralized autonomous corporations, but they are also not quite corporations — you can't hard fork Microsoft. They are kind of like open source software projects, but they are not quite that either — you can fork a blockchain, but not quite as easily as you can fork OpenOffice.These cryptoeconomic networks come in many flavors — ASIC-based PoW, GPU-based PoW, naive PoS, delegated PoS, hopefully soon Casper PoS — and each of these flavors inevitably comes with its own underlying philosophy. One well-known example is the maximalist vision of proof of work, where "the" correct blockchain, singular, is defined as the chain that miners have burned the largest amount of economic capital to create. Originally a mere in-protocol fork choice rule, this mechanism has in many cases been elevated to a sacred tenet — see this Twitter discussion between myself and Chris DeRose for an example of someone seriously trying to defend the idea in a pure form, even in the face of hash-algorithm-changing protocol hard forks. Bitshares' delegated proof of stake presents another coherent philosophy, where everything once again flows from a single tenet, but one that can be described even more simply: shareholders vote.Each of these philosophies; Nakamoto consensus, social consensus, shareholder voting consensus, leads to its own set of conclusions and leads to a system of values that makes quite a bit of sense when viewed on its own terms — though they can certainly be criticized when compared against each other. Casper consensus has a philosophical underpinning too, though one that has so far not been as succinctly articulated.Myself, Vlad, Dominic, Jae and others all have their own views on why proof of stake protocols exist and how to design them, but here I intend to explain where I personally am coming from.I'll proceed to listing observations and then conclusions directly.Cryptography is truly special in the 21st century because cryptography is one of the very few fields where adversarial conflict continues to heavily favor the defender. Castles are far easier to destroy than build, islands are defendable but can still be attacked, but an average person's ECC keys are secure enough to resist even state-level actors. Cypherpunk philosophy is fundamentally about leveraging this precious asymmetry to create a world that better preserves the autonomy of the individual, and cryptoeconomics is to some extent an extension of that, except this time protecting the safety and liveness of complex systems of coordination and collaboration, rather than simply the integrity and confidentiality of private messages. Systems that consider themselves ideological heirs to the cypherpunk spirit should maintain this basic property, and be much more expensive to destroy or disrupt than they are to use and maintain. The "cypherpunk spirit" isn't just about idealism; making systems that are easier to defend than they are to attack is also simply sound engineering. On medium to long time scales, humans are quite good at consensus. Even if an adversary had access to unlimited hashing power, and came out with a 51% attack of any major blockchain that reverted even the last month of history, convincing the community that this chain is legitimate is much harder than just outrunning the main chain's hashpower. They would need to subvert block explorers, every trusted member in the community, the New York Times, archive.org, and many other sources on the internet; all in all, convincing the world that the new attack chain is the one that came first in the information technology-dense 21st century is about as hard as convincing the world that the US moon landings never happened. These social considerations are what ultimately protect any blockchain in the long term, regardless of whether or not the blockchain's community admits it (note that Bitcoin Core does admit this primacy of the social layer). However, a blockchain protected by social consensus alone would be far too inefficient and slow, and too easy for disagreements to continue without end (though despite all difficulties, it has happened); hence, economic consensus serves an extremely important role in protecting liveness and safety properties in the short term. Because proof of work security can only come from block rewards (in Dominic Williams' terms, it lacks two of the three Es), and incentives to miners can only come from the risk of them losing their future block rewards, proof of work necessarily operates on a logic of massive power incentivized into existence by massive rewards. Recovery from attacks in PoW is very hard: the first time it happens, you can hard fork to change the PoW and thereby render the attacker's ASICs useless, but the second time you no longer have that option, and so the attacker can attack again and again. Hence, the size of the mining network has to be so large that attacks are inconceivable. Attackers of size less than X are discouraged from appearing by having the network constantly spend X every single day. I reject this logic because (i) it kills trees, and (ii) it fails to realize the cypherpunk spirit — cost of attack and cost of defense are at a 1:1 ratio, so there is no defender's advantage. Proof of stake breaks this symmetry by relying not on rewards for security, but rather penalties. Validators put money ("deposits") at stake, are rewarded slightly to compensate them for locking up their capital and maintaining nodes and taking extra precaution to ensure their private key safety, but the bulk of the cost of reverting transactions comes from penalties that are hundreds or thousands of times larger than the rewards that they got in the meantime. The "one-sentence philosophy" of proof of stake is thus not "security comes from burning energy", but rather "security comes from putting up economic value-at-loss". A given block or state has $X security if you can prove that achieving an equal level of finalization for any conflicting block or state cannot be accomplished unless malicious nodes complicit in an attempt to make the switch pay $X worth of in-protocol penalties. Theoretically, a majority collusion of validators may take over a proof of stake chain, and start acting maliciously. However, (i) through clever protocol design, their ability to earn extra profits through such manipulation can be limited as much as possible, and more importantly (ii) if they try to prevent new validators from joining, or execute 51% attacks, then the community can simply coordinate a hard fork and delete the offending validators' deposits. A successful attack may cost $50 million, but the process of cleaning up the consequences will not be that much more onerous than the geth/parity consensus failure of 2016.11.25. Two days later, the blockchain and community are back on track, attackers are $50 million poorer, and the rest of the community is likely richer since the attack will have caused the value of the token to go up due to the ensuing supply crunch. That's attack/defense asymmetry for you. The above should not be taken to mean that unscheduled hard forks will become a regular occurrence; if desired, the cost of a single 51% attack on proof of stake can certainly be set to be as high as the cost of a permanent 51% attack on proof of work, and the sheer cost and ineffectiveness of an attack should ensure that it is almost never attempted in practice. Economics is not everything. Individual actors may be motivated by extra-protocol motives, they may get hacked, they may get kidnapped, or they may simply get drunk and decide to wreck the blockchain one day and to hell with the cost. Furthermore, on the bright side, individuals' moral forbearances and communication inefficiencies will often raise the cost of an attack to levels much higher than the nominal protocol-defined value-at-loss. This is an advantage that we cannot rely on, but at the same time it is an advantage that we should not needlessly throw away. Hence, the best protocols are protocols that work well under a variety of models and assumptions— economic rationality with coordinated choice, economic rationality with individual choice, simple fault tolerance, Byzantine fault tolerance (ideally both the adaptive and non-adaptive adversary variants), Ariely/Kahneman-inspired behavioral economic models ("we all cheat just a little") and ideally any other model that's realistic and practical to reason about. It is important to have both layers of defense: economic incentives to discourage centralized cartels from acting anti-socially, and anti-centralization incentives to discourage cartels from forming in the first place. Consensus protocols that work as-fast-as-possible have risks and should be approached very carefully if at all, because if the possibility to be very fast is tied to incentives to do so, the combination will reward very high and systemic-risk-inducing levels of network-level centralization (eg. all validators running from the same hosting provider). Consensus protocols that don't care too much how fast a validator sends a message, as long as they do so within some acceptably long time interval (eg. 4–8 seconds, as we empirically know that latency in ethereum is usually ~500ms-1s) do not have these concerns. A possible middle ground is creating protocols that can work very quickly, but where mechanics similar to Ethereum's uncle mechanism ensure that the marginal reward for a node increasing its degree of network connectivity beyond some easily attainable point is fairly low. From here, there are of course many details and many ways to diverge on the details, but the above are the core principles that at least my version of Casper is based on. From here, we can certainly debate tradeoffs between competing values . Do we give ETH a 1% annual issuance rate and get an $50 million cost of forcing a remedial hard fork, or a zero annual issuance rate and get a $5 million cost of forcing a remedial hard fork? When do we increase a protocol's security under the economic model in exchange for decreasing its security under a fault tolerance model? Do we care more about having a predictable level of security or a predictable level of issuance? These are all questions for another post, and the various ways of implementing the different tradeoffs between these values are questions for yet more posts. But we'll get to it :) -
 白话区块链入门062 | 中本聪是如何完全匿名的?全世界人肉搜索都无可奈何 白话区块链从入门到精通,看我就够了!「白话区块链入门」系列让零基础的小伙伴也能轻松入门,欢迎大家在文末点赞留言,说说你最想了解的区块链小知识,参与有奖哦!作者 | 郭立芳出品|白话区块链(ID:hellobtc)区块链世界里最神秘的人,非比特币发明者中本聪莫属。一直以来,关于他的江湖传说不断,就像秦始皇陵园,只知道存在过,不知道是怎样的一个存在。现在唯一可以确定的是,中本聪是比特币的第一个矿工,据估计,中本聪拥有近100万个比特币。在网络如此发达的今天,中本聪是如何做到“隐身”的呢? 01 中本聪可查的轨迹白话区块链(ID: hellobtc)先带大家回顾一下,中本聪从出现到消失的行动轨迹:2008年11月1日,中本聪发表了题为《比特币:一种点对点式的电子现金系统》的论文,第一次昭告天下,他发明了比特币。2009年1月3日,中本聪挖出了第一个比特币区块,也称创世区块,并获得了50个比特币的系统奖励。2009年2月11日,中本聪注册了P2P Foundation,资料显示,中本聪是一个43岁的日本男性,至于该信息是真实的,还是中本聪的障眼法,不得而知。当天,中本聪在上面声称,他开发了一个叫比特币的电子现金系统,并给出了开源代码。2010年12月5日,在维基解密泄露美国外交电报事件期间,比特币社区呼吁维基解密接受比特币捐款,以打破封锁。为保护襁褓中的比特币,中本聪义无反顾地站出来,坚决反对捐款,他的理由是:比特币还很弱小,经不起冲击和争议。2010年12月12日,中本聪在比特币论坛中发表了最后一篇文章,提及了最新版本软件中的一些小问题。此后,仅通过电子邮件与比特币核心开发团队的少数人保持联系,不再公开发表任何言论。2011年4月26日,中本聪在一封电子邮件中写道:“我已转移到其他事物上去了。”从此,中本聪的电子邮件关闭了。2014年,Newsweek发布新闻,表示自己找到了中本聪本人——多利安·中本聪;9月13日,中本聪突然发帖否认此事,随后,多利安·中本聪也表示,自己并不是比特币创始人中本聪。▲ 多利安·中本聪2018年11月29日,时隔多年的“中本聪”账号发布了仅有一词的状态“Nour”,引起比特币社区热议,但不知是黑客入侵还是真的中本聪在操作。 02 中本聪是如何“隐身”的呢?令人费解的是,现在互联网如此发达,政府、媒体、比特币爱好者、黑客等各路人马都在想尽办法“人肉搜索”中本聪,但到目前为止依然一无所获。“中本聪到底是谁”,这一问题成了币圈最大的迷案。那么,问题来了,中本聪是怎么做到成功“隐身”的呢?答案是,因为他行事缜密细致,且隐藏能力高超。他在2008年8月18号就注册了「http://bitcoin.org」的域名,并保护性注册了「http://bitcoin.net」。中本聪选择的那家域名注册商,能为用户的域名注册提供匿名性保证,确保不被人肉搜索到,也不会遭到政府的检索,而事实证明,他们做到了,中本聪没有看错。为了隐藏自己,中本聪使用Tor浏览器(一种加密浏览器)发送邮件,与任何人交流都使用PGP加密和Tor网络,哪怕与最亲密的合作伙伴交流也加密,而且从不透露个人信息。他还用上了伪装英式拼读、 使用日本名字、模仿别人的写作风格等等障眼法,效果不错。现在,虽然有无数研究者、情报人员调查过他的真实身份,但至今未得到核实。 03中本聪的各种“版本”坊间流传的“中本聪”版本,主要有这么5种:1、外星人有人大胆猜想,是不是像科幻电影里常见的剧情,一个月黑星高的夜晚,外星人中本聪乘坐飞碟,悄无声息地来到地球,把比特币的开源代码传到互联网上。当他的光荣使命完成后,又选择了默默地离开,不带走一片云彩。2、未来穿越者有人开脑洞地认为,中本聪可能是未来人,为了平衡目前经济社会的资本,穿越到了这个时代,创造了比特币。3、已离世有人猜想,中本聪有可能得了重病或者遭遇意外,在2011年便去世了,因此中本聪掌握的比特币私钥也一起消失了,100多万个比特币将永久沉睡。4、一个团队有人研究了比特币的代码,认为太精妙了,不像单个人所为,更像一个团队写的。可能这个团队都是顶尖人才,创造比特币是一个长久以来的计划,酝酿了几年时间,最后才慢慢成型的。5、英国人理由是,他会用很溜的英式英语,他的活动时差显示他主要生活在美国,加上他取了一个日本名字,所以说,他是披着日本外衣在美国生活的英国人。但这些特征,也可能是中本聪用的障眼法。最后,你可能会好奇地问,有了这么伟大的成就,有了巨大的财富,为什么中本聪还要隐藏自己呀?其中一个猜测是,可能中本聪对去中心化的理念非常执着,他觉得只有自己消失,比特币的系统才会是安全的去中心化。试想一下,中本聪若仍在,比特币基金会必然仍由其领导,如果政府批捕中本聪,将会给比特币社区带来毁灭性的打击。不管中本聪是“他”,是“他们”,还是“它”,中本聪已经改变了这个世界,每一个为比特币做过贡献的或者正在做贡献的人,其实都是中本聪!以上5种猜测(外星人、未来穿越者、已离世、一个团队、英国人),你最认可哪种猜测?为什么?欢迎在留言区留言。「白话区块链入门系列」互动有奖本文发布2小时内的第1位精选留言,奖励8.8元红包;指出本文事例、逻辑等重大错误、并提出优秀建议的留言,一经采纳,奖励50元;本系列接受读者投稿,录用稿件每篇奖励300元。后台回复「投稿」获取详细信息。往期内容精选♢006 比特币的矿工和挖矿是什么意思?♢014 虚拟货币价值的本质是什么?♢015 神奇而有趣的比特币♢018 被称为“区块链2.0”的以太坊是什么?♢021 被称为“区块链3.0”的EOS是什么?★后台回复「入门」获取完整目录!★——End——『声明:本文为作者独立观点,不代表白话区块链立场,亦不构成任何投资意见或建议。』亲,给「白话区块链」加个“星标” ???? 不错过重要推送哦 ????亲,据说99.9%有品位的人都点了「好看」????
白话区块链入门062 | 中本聪是如何完全匿名的?全世界人肉搜索都无可奈何 白话区块链从入门到精通,看我就够了!「白话区块链入门」系列让零基础的小伙伴也能轻松入门,欢迎大家在文末点赞留言,说说你最想了解的区块链小知识,参与有奖哦!作者 | 郭立芳出品|白话区块链(ID:hellobtc)区块链世界里最神秘的人,非比特币发明者中本聪莫属。一直以来,关于他的江湖传说不断,就像秦始皇陵园,只知道存在过,不知道是怎样的一个存在。现在唯一可以确定的是,中本聪是比特币的第一个矿工,据估计,中本聪拥有近100万个比特币。在网络如此发达的今天,中本聪是如何做到“隐身”的呢? 01 中本聪可查的轨迹白话区块链(ID: hellobtc)先带大家回顾一下,中本聪从出现到消失的行动轨迹:2008年11月1日,中本聪发表了题为《比特币:一种点对点式的电子现金系统》的论文,第一次昭告天下,他发明了比特币。2009年1月3日,中本聪挖出了第一个比特币区块,也称创世区块,并获得了50个比特币的系统奖励。2009年2月11日,中本聪注册了P2P Foundation,资料显示,中本聪是一个43岁的日本男性,至于该信息是真实的,还是中本聪的障眼法,不得而知。当天,中本聪在上面声称,他开发了一个叫比特币的电子现金系统,并给出了开源代码。2010年12月5日,在维基解密泄露美国外交电报事件期间,比特币社区呼吁维基解密接受比特币捐款,以打破封锁。为保护襁褓中的比特币,中本聪义无反顾地站出来,坚决反对捐款,他的理由是:比特币还很弱小,经不起冲击和争议。2010年12月12日,中本聪在比特币论坛中发表了最后一篇文章,提及了最新版本软件中的一些小问题。此后,仅通过电子邮件与比特币核心开发团队的少数人保持联系,不再公开发表任何言论。2011年4月26日,中本聪在一封电子邮件中写道:“我已转移到其他事物上去了。”从此,中本聪的电子邮件关闭了。2014年,Newsweek发布新闻,表示自己找到了中本聪本人——多利安·中本聪;9月13日,中本聪突然发帖否认此事,随后,多利安·中本聪也表示,自己并不是比特币创始人中本聪。▲ 多利安·中本聪2018年11月29日,时隔多年的“中本聪”账号发布了仅有一词的状态“Nour”,引起比特币社区热议,但不知是黑客入侵还是真的中本聪在操作。 02 中本聪是如何“隐身”的呢?令人费解的是,现在互联网如此发达,政府、媒体、比特币爱好者、黑客等各路人马都在想尽办法“人肉搜索”中本聪,但到目前为止依然一无所获。“中本聪到底是谁”,这一问题成了币圈最大的迷案。那么,问题来了,中本聪是怎么做到成功“隐身”的呢?答案是,因为他行事缜密细致,且隐藏能力高超。他在2008年8月18号就注册了「http://bitcoin.org」的域名,并保护性注册了「http://bitcoin.net」。中本聪选择的那家域名注册商,能为用户的域名注册提供匿名性保证,确保不被人肉搜索到,也不会遭到政府的检索,而事实证明,他们做到了,中本聪没有看错。为了隐藏自己,中本聪使用Tor浏览器(一种加密浏览器)发送邮件,与任何人交流都使用PGP加密和Tor网络,哪怕与最亲密的合作伙伴交流也加密,而且从不透露个人信息。他还用上了伪装英式拼读、 使用日本名字、模仿别人的写作风格等等障眼法,效果不错。现在,虽然有无数研究者、情报人员调查过他的真实身份,但至今未得到核实。 03中本聪的各种“版本”坊间流传的“中本聪”版本,主要有这么5种:1、外星人有人大胆猜想,是不是像科幻电影里常见的剧情,一个月黑星高的夜晚,外星人中本聪乘坐飞碟,悄无声息地来到地球,把比特币的开源代码传到互联网上。当他的光荣使命完成后,又选择了默默地离开,不带走一片云彩。2、未来穿越者有人开脑洞地认为,中本聪可能是未来人,为了平衡目前经济社会的资本,穿越到了这个时代,创造了比特币。3、已离世有人猜想,中本聪有可能得了重病或者遭遇意外,在2011年便去世了,因此中本聪掌握的比特币私钥也一起消失了,100多万个比特币将永久沉睡。4、一个团队有人研究了比特币的代码,认为太精妙了,不像单个人所为,更像一个团队写的。可能这个团队都是顶尖人才,创造比特币是一个长久以来的计划,酝酿了几年时间,最后才慢慢成型的。5、英国人理由是,他会用很溜的英式英语,他的活动时差显示他主要生活在美国,加上他取了一个日本名字,所以说,他是披着日本外衣在美国生活的英国人。但这些特征,也可能是中本聪用的障眼法。最后,你可能会好奇地问,有了这么伟大的成就,有了巨大的财富,为什么中本聪还要隐藏自己呀?其中一个猜测是,可能中本聪对去中心化的理念非常执着,他觉得只有自己消失,比特币的系统才会是安全的去中心化。试想一下,中本聪若仍在,比特币基金会必然仍由其领导,如果政府批捕中本聪,将会给比特币社区带来毁灭性的打击。不管中本聪是“他”,是“他们”,还是“它”,中本聪已经改变了这个世界,每一个为比特币做过贡献的或者正在做贡献的人,其实都是中本聪!以上5种猜测(外星人、未来穿越者、已离世、一个团队、英国人),你最认可哪种猜测?为什么?欢迎在留言区留言。「白话区块链入门系列」互动有奖本文发布2小时内的第1位精选留言,奖励8.8元红包;指出本文事例、逻辑等重大错误、并提出优秀建议的留言,一经采纳,奖励50元;本系列接受读者投稿,录用稿件每篇奖励300元。后台回复「投稿」获取详细信息。往期内容精选♢006 比特币的矿工和挖矿是什么意思?♢014 虚拟货币价值的本质是什么?♢015 神奇而有趣的比特币♢018 被称为“区块链2.0”的以太坊是什么?♢021 被称为“区块链3.0”的EOS是什么?★后台回复「入门」获取完整目录!★——End——『声明:本文为作者独立观点,不代表白话区块链立场,亦不构成任何投资意见或建议。』亲,给「白话区块链」加个“星标” ???? 不错过重要推送哦 ????亲,据说99.9%有品位的人都点了「好看」???? -
 017:Solidity语法之数组|《ETH原理与智能合约开发》笔记 待字闺中开发了一门区块链方面的课程:《深入浅出ETH原理与智能合约开发》,马良老师讲授。此简书文集记录我的学习笔记。课程共8节课。其中,前四课讲ETH原理,后四课讲智能合约。第六课分为三部分:Solidity语法之数组 Solidity语法之合约 Truffle简介与使用 这篇文章是第六课第一部分的学习笔记:Solidity语法之数组。上一小节简要介绍了 Solidity 的基础语法。还有两部分重要的内容要重点讲解一下,分别是数组和合约。这节课主要讲解 Solidity 数组相关知识,并有若干实例辅助理解。1、动态数组,bytes,string数组知识点在Solidity语法中,数组中主要有两种。一种是动态数组,主要是storage类型;另一种是定长数组,一般是memory类型。在这两个类型之外,还有两种特殊的类型,一是字节数组(bytes),一个是字符串(string),通常字符串可以转换成字节数组。1.1 动态数组length 在声明后可以改变,从而调整数组大小(静态数组不可以)。 push 向数组尾部附加一个元素,返回新的 length 。 bytes 数组指的是原始的字节串。其它类型(例如byte)的动态数组一个元素会占32字节,但是bytes每一个元素就是一个字节(更为紧凑,节省GAS)。可以把String 转换为 bytes 。对于定长的bytes,index 操作是只读!这里要特别注意。而对动态数组,index操作是可读写! delete 只是 reset 该元素(重置为0),并不是通常意义的删除。【例子②】 1.2 字符串UTF-8 编码的结果。没有length 的概念。 UTF-8 是变长的编码方式,1-4个字节表示一个符号。对于英文和ASCII码是相同的。中文常见是3个字节。 所以String的长度一般是通过转化为 bytes 数组后,只能得到 bytes 数组的长度。 缺乏缺省的各类 string 操作,需要库支持(比如strcmp,strlen)。 bytes 无法直接转换到string,需要库支持。后面这两条是不完善的地方,不方便编程。 后面通过例子来理解这些知识点。2、实例讲解2.0 概览对于动态数组,讲解四个知识点:uint 动态数组【例子①】 bytes 定长数组【例子①】 string转换bytes【例子③】 手动的删除【例子②⑤】 对于字符串,讲解两个知识点:字符串的长度。根据 UTF-8 编码的规定来计算字符长度。【例子③】 字符串的比较。Keccak256 取巧的办法。【例子④】 演示代码在老师的代码托管网站上,获取方法见第二课第3小节。2.1 例子①拉取代码后,用 Remix 打开 example_1.sol 文件。在 settings 设置 Solidity version 为0.4.17,不要太高。本课的例子操作:点 Deploy 部署。 点 TestArray 执行。再看控制台,可以看到 TestArray 函数的返回值:bts1的长度变成了5。 点控制台上的debug,调试。 点击行号可以设置断点,此处演示把57行和69行设置为断点。右边可以在 solidity state 和 solidity locals 看到各变量的值。 点击调试按钮,最后一个:跳到下一个断点。执行结果1 点击调试按钮(第一行最后一个按钮),使走完一个循环。执行结果2 可以看到:ex_1的第0个元素发生了变化,bts2 变成了0x09020304。再点击几次“跳到下一个断点”按钮。使跳出循环。执行结果3 可以看到:bts1 变成了0x0506070809,bts2 变成了0x09020304。点击memory,可以看到变量在内存中的存储情况。 变量的存储ex_1,见代码第48行,byte 就是bytes1 ,ex_1是字节数组(见47行注释)。它的每一个元素都是32字节。如图上半部分四个小框。而bts1,是原始字节串,整个元素占一个字节。它不能按偏移量修改,能整体修改。如图下半部分。点击停止按钮。结束调试。 2.2 例子② 删除操作:修改代码。取消注释82行,注释掉84行,先演示默认删除的效果。 重新部署代码。Deploy 点击TestDelete,观察到返回值为4,意思是并没有删除,只是清零了。默认删除效果 取消注释84行,注释掉82行。再观察手动删除效果。这里使用了137行的自定义函数。实现方法是:把待删除位置之后的元素都向前移动一位,把最后一个元素置0,再把长度减少1。调试结果如图。手动删除效果返回值为长度3,88被删除了。 2.3 例子③ 字符串长度如果返回值是第38行,返回6;如果返回返回值是40行,则是2。后者符合期望值。实现方法在代码的第114行。(对UTF-8不懂,先放下不看)2.4 例子④ 字符串比较通过计算 Keccak256 ,如果这个值相等,则字符串是相等的。(演示略)2.5 例子⑤ 映射的删除默认的删除操作也是只清零,并没有真的删除(演示略)。编程时要注意。小结一下,本节通过例子介绍了solidity数组和字符串的使用。不足之处,请批评指正。
017:Solidity语法之数组|《ETH原理与智能合约开发》笔记 待字闺中开发了一门区块链方面的课程:《深入浅出ETH原理与智能合约开发》,马良老师讲授。此简书文集记录我的学习笔记。课程共8节课。其中,前四课讲ETH原理,后四课讲智能合约。第六课分为三部分:Solidity语法之数组 Solidity语法之合约 Truffle简介与使用 这篇文章是第六课第一部分的学习笔记:Solidity语法之数组。上一小节简要介绍了 Solidity 的基础语法。还有两部分重要的内容要重点讲解一下,分别是数组和合约。这节课主要讲解 Solidity 数组相关知识,并有若干实例辅助理解。1、动态数组,bytes,string数组知识点在Solidity语法中,数组中主要有两种。一种是动态数组,主要是storage类型;另一种是定长数组,一般是memory类型。在这两个类型之外,还有两种特殊的类型,一是字节数组(bytes),一个是字符串(string),通常字符串可以转换成字节数组。1.1 动态数组length 在声明后可以改变,从而调整数组大小(静态数组不可以)。 push 向数组尾部附加一个元素,返回新的 length 。 bytes 数组指的是原始的字节串。其它类型(例如byte)的动态数组一个元素会占32字节,但是bytes每一个元素就是一个字节(更为紧凑,节省GAS)。可以把String 转换为 bytes 。对于定长的bytes,index 操作是只读!这里要特别注意。而对动态数组,index操作是可读写! delete 只是 reset 该元素(重置为0),并不是通常意义的删除。【例子②】 1.2 字符串UTF-8 编码的结果。没有length 的概念。 UTF-8 是变长的编码方式,1-4个字节表示一个符号。对于英文和ASCII码是相同的。中文常见是3个字节。 所以String的长度一般是通过转化为 bytes 数组后,只能得到 bytes 数组的长度。 缺乏缺省的各类 string 操作,需要库支持(比如strcmp,strlen)。 bytes 无法直接转换到string,需要库支持。后面这两条是不完善的地方,不方便编程。 后面通过例子来理解这些知识点。2、实例讲解2.0 概览对于动态数组,讲解四个知识点:uint 动态数组【例子①】 bytes 定长数组【例子①】 string转换bytes【例子③】 手动的删除【例子②⑤】 对于字符串,讲解两个知识点:字符串的长度。根据 UTF-8 编码的规定来计算字符长度。【例子③】 字符串的比较。Keccak256 取巧的办法。【例子④】 演示代码在老师的代码托管网站上,获取方法见第二课第3小节。2.1 例子①拉取代码后,用 Remix 打开 example_1.sol 文件。在 settings 设置 Solidity version 为0.4.17,不要太高。本课的例子操作:点 Deploy 部署。 点 TestArray 执行。再看控制台,可以看到 TestArray 函数的返回值:bts1的长度变成了5。 点控制台上的debug,调试。 点击行号可以设置断点,此处演示把57行和69行设置为断点。右边可以在 solidity state 和 solidity locals 看到各变量的值。 点击调试按钮,最后一个:跳到下一个断点。执行结果1 点击调试按钮(第一行最后一个按钮),使走完一个循环。执行结果2 可以看到:ex_1的第0个元素发生了变化,bts2 变成了0x09020304。再点击几次“跳到下一个断点”按钮。使跳出循环。执行结果3 可以看到:bts1 变成了0x0506070809,bts2 变成了0x09020304。点击memory,可以看到变量在内存中的存储情况。 变量的存储ex_1,见代码第48行,byte 就是bytes1 ,ex_1是字节数组(见47行注释)。它的每一个元素都是32字节。如图上半部分四个小框。而bts1,是原始字节串,整个元素占一个字节。它不能按偏移量修改,能整体修改。如图下半部分。点击停止按钮。结束调试。 2.2 例子② 删除操作:修改代码。取消注释82行,注释掉84行,先演示默认删除的效果。 重新部署代码。Deploy 点击TestDelete,观察到返回值为4,意思是并没有删除,只是清零了。默认删除效果 取消注释84行,注释掉82行。再观察手动删除效果。这里使用了137行的自定义函数。实现方法是:把待删除位置之后的元素都向前移动一位,把最后一个元素置0,再把长度减少1。调试结果如图。手动删除效果返回值为长度3,88被删除了。 2.3 例子③ 字符串长度如果返回值是第38行,返回6;如果返回返回值是40行,则是2。后者符合期望值。实现方法在代码的第114行。(对UTF-8不懂,先放下不看)2.4 例子④ 字符串比较通过计算 Keccak256 ,如果这个值相等,则字符串是相等的。(演示略)2.5 例子⑤ 映射的删除默认的删除操作也是只清零,并没有真的删除(演示略)。编程时要注意。小结一下,本节通过例子介绍了solidity数组和字符串的使用。不足之处,请批评指正。 -
 018:Solidity语法之合约|《ETH原理与智能合约开发》笔记 待字闺中开发了一门区块链方面的课程:《深入浅出ETH原理与智能合约开发》,马良老师讲授。此简书文集记录我的学习笔记。课程共8节课。其中,前四课讲ETH原理,后四课讲智能合约。第六课分为三部分:Solidity语法之数组 Solidity语法之合约 Truffle简介与使用 这篇文章是第六课第二部分的学习笔记:Solidity语法之合约。第5课第3小节简要介绍了 Solidity 的基础语法。还有两部分重要的内容要重点讲解一下,分别是数组和合约。这节课主要讲解Solidity合约相关知识,并有若干实例辅助理解。1、合约相关知识点合约相关知识点1.1 合约调用合约间接口相互调用□ address.function(para)□ address.call(func_signature, para) 合约之间转账□ address.transfer()□ address.send()□ address.call()□ - address.call.gas(num).value(num)() 缺省的是使用所有可用的Gas 调用深度是1024。一般正常情况不会这么多,除非发生递归。 delegatecode(),主要是调用库函数,但还是在当前函数的上下文环境。(第四课出现过) 1.1 转账需要注意的问题可以收钱的接口需要payable。 转账会触发接收账户的fallback函数(payable)。fallback函数,一个匿名函数。 transfer 仅仅转发2300 gas, 失败会抛出异常。fallback 要非常简单。 send 仅仅转发2300 gas, 失败只会返回false。fallback 要非常简单。 call.value(amount)() 会转发全部的可用的gas,失败只会返回false,容易引起重入型攻击。 2、合约相关实例1、合约间接口调用实例代码见git仓库,或见下图。合约间接口调用实例打开文件 example_2.sol ,编译。 在 run 页面,选择 B_caller ,点击 Deploy 。下面出现三个接口。B合约的三个接口 在调用合约前,先显示一下A的状态值,点 Getstate_A,显示为0。 显式调用,点击Invocate_A,再点击 Getstate_A,结果为15,正确。 call调用。点击 Call_A ,返回值为真。再点击 Getstate_A,结果为23,正确。 特别注意:代码第45行。keccak256在计算签名时,函数的参数要写全称uint256,不要写简称uint,否则会出现问题。因为签名算法是根据字符串算的,它不会自动把简称替换成全称。1、合约间接口调用实例合约转账实例关闭example_2.sol,打开example_3.sol,(有时需要刷新一下浏览器) 编译,或勾上自动编译。 在 run 页面,选择 B_caller ,点击 Deploy 。下面出现四个接口。B合约的三个接口 在调用合约前,先显示一下A的状态值,点 Getbalance_A,显示为0。 Value值输入6666,点击 Transfer_A,再点击 Getbalance_A,结果为6666,正确。 Value值输入8888,点击 Sender_A ,返回值为真。再点击 Getbalance_A,结果为15554,正确。 Value值输入1,点击Call_A,返回值为真。再点击 Getbalance_A,结果为15555,正确。 以上是将9~11行注释掉的情况。现在去掉这三行的注释,再操作一遍。Transfer_A、Sender_A 操作均失败, Call_A 成功。而把49行代码换成第48行代码时,又会转账失败。其中,9~11的三行代码会消耗6万个Gas 。transfer、send 仅仅转发2300个Gas,所以会失败。而Call调用方法,缺省是支付所有Gas,在本例中若限制5万个Gas,则转账失败。小结一下,本小节主要讲解了 Solidity 合约相关知识,并有两个实例辅助理解。不足之处,请批评指正。
018:Solidity语法之合约|《ETH原理与智能合约开发》笔记 待字闺中开发了一门区块链方面的课程:《深入浅出ETH原理与智能合约开发》,马良老师讲授。此简书文集记录我的学习笔记。课程共8节课。其中,前四课讲ETH原理,后四课讲智能合约。第六课分为三部分:Solidity语法之数组 Solidity语法之合约 Truffle简介与使用 这篇文章是第六课第二部分的学习笔记:Solidity语法之合约。第5课第3小节简要介绍了 Solidity 的基础语法。还有两部分重要的内容要重点讲解一下,分别是数组和合约。这节课主要讲解Solidity合约相关知识,并有若干实例辅助理解。1、合约相关知识点合约相关知识点1.1 合约调用合约间接口相互调用□ address.function(para)□ address.call(func_signature, para) 合约之间转账□ address.transfer()□ address.send()□ address.call()□ - address.call.gas(num).value(num)() 缺省的是使用所有可用的Gas 调用深度是1024。一般正常情况不会这么多,除非发生递归。 delegatecode(),主要是调用库函数,但还是在当前函数的上下文环境。(第四课出现过) 1.1 转账需要注意的问题可以收钱的接口需要payable。 转账会触发接收账户的fallback函数(payable)。fallback函数,一个匿名函数。 transfer 仅仅转发2300 gas, 失败会抛出异常。fallback 要非常简单。 send 仅仅转发2300 gas, 失败只会返回false。fallback 要非常简单。 call.value(amount)() 会转发全部的可用的gas,失败只会返回false,容易引起重入型攻击。 2、合约相关实例1、合约间接口调用实例代码见git仓库,或见下图。合约间接口调用实例打开文件 example_2.sol ,编译。 在 run 页面,选择 B_caller ,点击 Deploy 。下面出现三个接口。B合约的三个接口 在调用合约前,先显示一下A的状态值,点 Getstate_A,显示为0。 显式调用,点击Invocate_A,再点击 Getstate_A,结果为15,正确。 call调用。点击 Call_A ,返回值为真。再点击 Getstate_A,结果为23,正确。 特别注意:代码第45行。keccak256在计算签名时,函数的参数要写全称uint256,不要写简称uint,否则会出现问题。因为签名算法是根据字符串算的,它不会自动把简称替换成全称。1、合约间接口调用实例合约转账实例关闭example_2.sol,打开example_3.sol,(有时需要刷新一下浏览器) 编译,或勾上自动编译。 在 run 页面,选择 B_caller ,点击 Deploy 。下面出现四个接口。B合约的三个接口 在调用合约前,先显示一下A的状态值,点 Getbalance_A,显示为0。 Value值输入6666,点击 Transfer_A,再点击 Getbalance_A,结果为6666,正确。 Value值输入8888,点击 Sender_A ,返回值为真。再点击 Getbalance_A,结果为15554,正确。 Value值输入1,点击Call_A,返回值为真。再点击 Getbalance_A,结果为15555,正确。 以上是将9~11行注释掉的情况。现在去掉这三行的注释,再操作一遍。Transfer_A、Sender_A 操作均失败, Call_A 成功。而把49行代码换成第48行代码时,又会转账失败。其中,9~11的三行代码会消耗6万个Gas 。transfer、send 仅仅转发2300个Gas,所以会失败。而Call调用方法,缺省是支付所有Gas,在本例中若限制5万个Gas,则转账失败。小结一下,本小节主要讲解了 Solidity 合约相关知识,并有两个实例辅助理解。不足之处,请批评指正。 -
 019:Truffle简介与使用|《ETH原理与智能合约开发》笔记 待字闺中开发了一门区块链方面的课程:《深入浅出ETH原理与智能合约开发》,马良老师讲授。此简书文集记录我的学习笔记。课程共8节课。其中,前四课讲ETH原理,后四课讲智能合约。第六课分为三部分:Solidity语法之数组 Solidity语法之合约 Truffle简介与使用 这篇文章是第六课第三部分的学习笔记:Truffle简介与使用。这节课主要讲解了 Truffle 的技术特性,并演示了 Truffle 的安装和一个小例子。1、Truffle 简介前面介绍的 Remix 作为学习工具来用是比较好的,但是不能满足生产环境。因为 Remix 不支持 web 前端、自动化程度不是很高,不方便进行自动化测试。实际工作中用到的是Truffle框架。1.1 技术特性Consensys 出品,智能合约开发测试框架 内置的编译 / 链接 / 部署 快速开发自动合约测试 可以部署到 TESTRPC/ 测试网络 / 主网(TESTRPC现在更名为ganache) 直接可与合约通信的交互 Console 调试合约 集成了 web / javascript 组件,可以直接运行 App web 前端 1.2 安装要求ubuntu 16.04 Nodejs LTS 8.11 ganache-cli 为测试网络(速度快,不需要挖矿。) 2、Truffle 开发演示马老师把演示的步骤放在了代码仓库:lesson_6/truffle_setup.txt 。下面是我的操作记录。2.1 Truffle 安装安装NVM。Truffle 是基于 Node.js 开发的,使用时需要node的版本在 8.0 以上,管理版本用的工具是Nvm。安装命令如下: curl -o- https://raw.githubusercontent.com/creationix/nvm/v0.33.9/install.sh | bash 确认各个软件都已安装齐。我这步出了点问题,重启了一下终端,好了。 sudo apt install build-essential python -y 退出终端exit,使安装的 nvm 生效。也可以不退出,使用如下命令,生成一个子进程。 exec bash 安装 node.js 的长期稳定版。我安装之后是8.11.2版。 nvm install --lts 再把 npm 更新一下。更新后版本是6.0 npm install -g npm 安装 Truffle 和 ganache,另外还要安装webpack并指定版本4.0 。我这步安装了20多分钟,电脑发热的厉害。最后安装成功,Truffle 的版本是4.1.9 npm install -g truffle ganache-cli webpack@4.0.0 2.2 Truffle 实例在工作目录新建一个文件夹。我的工作目录是ETHljx,新建文件夹是hello_world 。再进入到文件夹。 cd ~/ETHljx mkdir hello_world cd hello_world 用Truffle 生成一个自带的例子。这是一个很简单的例子,并不是ERC20的代币,仅作练习使用。 truffle unbox webpack 编译 truffle compile 编译后可以看到有三个 .sol 文件。主要是 MetaCoin.sol 文件。查看文件 vim contracts/MetaCoin.sol MetaCoin.sol代码查看完代码后,在命令模式下按 :q! 退出vim 。使用 tmux 再开一个窗口,启动ganache测试网络(右边窗口)。 ganache-cli -h 0.0.0.0 上面的命令是老师的,用的是两台机器,一个远程服务器。我的是在同一台电脑上练习,用下面的命令,即不加后面的参数:ganache-cli 启动后,可以看到10个账号,和对应的私钥。复制下来一个账号。端口号8545要记下来。部署合约(左边窗口) truffle migrate 修改 truffle.js 改端口号到 8545, ip 到本机对应的外部IP(非 127.0.0.1)。注意:前面这句是马老师的情况(使用两台机器),我用的一台机器,所以,IP还得写127.0.0.1 。(老师的是192.168.1.12) 修改 package.json,第8行的端口号8008 。 修改 app/javascript/app.js 修改ip地址和端口号 否则不能正常运行 vim app/javascript/app.js window.web3 = new Web3(new Web3.providers.HttpProvider("http://192.168.1.12:8545"));//这是老师的,IP和第13步一样;端口号改成8545。 window.web3 = new Web3(new Web3.providers.HttpProvider("http://127.0.0.1:8545"));//这是我的。 启动 npm run dev 在浏览器地址栏输入127.0.0.1:8008,打开web前端。可以看到当前有10000个Meta币。给刚才复制的账号转88个币,输入88,粘贴地址,点击Send MetaCoin。之后,余额少了88个币。再回到测试网络,可以看到,区块号增加了1。 演示结束。 Ctrl + Z:停止左边的 web 服务,Ctrl + B,→:切换到右边窗口,Ctrl + C:停止测试网络。exit:关闭一个tmux窗口,退出 tmux,退出默认的终端,都是这个命令。小结一下,本节简要介绍了Truffle的技术特性,演示了Truffle的安装过程,并运行了一个简单的实例。不足之处,请批评指正。
019:Truffle简介与使用|《ETH原理与智能合约开发》笔记 待字闺中开发了一门区块链方面的课程:《深入浅出ETH原理与智能合约开发》,马良老师讲授。此简书文集记录我的学习笔记。课程共8节课。其中,前四课讲ETH原理,后四课讲智能合约。第六课分为三部分:Solidity语法之数组 Solidity语法之合约 Truffle简介与使用 这篇文章是第六课第三部分的学习笔记:Truffle简介与使用。这节课主要讲解了 Truffle 的技术特性,并演示了 Truffle 的安装和一个小例子。1、Truffle 简介前面介绍的 Remix 作为学习工具来用是比较好的,但是不能满足生产环境。因为 Remix 不支持 web 前端、自动化程度不是很高,不方便进行自动化测试。实际工作中用到的是Truffle框架。1.1 技术特性Consensys 出品,智能合约开发测试框架 内置的编译 / 链接 / 部署 快速开发自动合约测试 可以部署到 TESTRPC/ 测试网络 / 主网(TESTRPC现在更名为ganache) 直接可与合约通信的交互 Console 调试合约 集成了 web / javascript 组件,可以直接运行 App web 前端 1.2 安装要求ubuntu 16.04 Nodejs LTS 8.11 ganache-cli 为测试网络(速度快,不需要挖矿。) 2、Truffle 开发演示马老师把演示的步骤放在了代码仓库:lesson_6/truffle_setup.txt 。下面是我的操作记录。2.1 Truffle 安装安装NVM。Truffle 是基于 Node.js 开发的,使用时需要node的版本在 8.0 以上,管理版本用的工具是Nvm。安装命令如下: curl -o- https://raw.githubusercontent.com/creationix/nvm/v0.33.9/install.sh | bash 确认各个软件都已安装齐。我这步出了点问题,重启了一下终端,好了。 sudo apt install build-essential python -y 退出终端exit,使安装的 nvm 生效。也可以不退出,使用如下命令,生成一个子进程。 exec bash 安装 node.js 的长期稳定版。我安装之后是8.11.2版。 nvm install --lts 再把 npm 更新一下。更新后版本是6.0 npm install -g npm 安装 Truffle 和 ganache,另外还要安装webpack并指定版本4.0 。我这步安装了20多分钟,电脑发热的厉害。最后安装成功,Truffle 的版本是4.1.9 npm install -g truffle ganache-cli webpack@4.0.0 2.2 Truffle 实例在工作目录新建一个文件夹。我的工作目录是ETHljx,新建文件夹是hello_world 。再进入到文件夹。 cd ~/ETHljx mkdir hello_world cd hello_world 用Truffle 生成一个自带的例子。这是一个很简单的例子,并不是ERC20的代币,仅作练习使用。 truffle unbox webpack 编译 truffle compile 编译后可以看到有三个 .sol 文件。主要是 MetaCoin.sol 文件。查看文件 vim contracts/MetaCoin.sol MetaCoin.sol代码查看完代码后,在命令模式下按 :q! 退出vim 。使用 tmux 再开一个窗口,启动ganache测试网络(右边窗口)。 ganache-cli -h 0.0.0.0 上面的命令是老师的,用的是两台机器,一个远程服务器。我的是在同一台电脑上练习,用下面的命令,即不加后面的参数:ganache-cli 启动后,可以看到10个账号,和对应的私钥。复制下来一个账号。端口号8545要记下来。部署合约(左边窗口) truffle migrate 修改 truffle.js 改端口号到 8545, ip 到本机对应的外部IP(非 127.0.0.1)。注意:前面这句是马老师的情况(使用两台机器),我用的一台机器,所以,IP还得写127.0.0.1 。(老师的是192.168.1.12) 修改 package.json,第8行的端口号8008 。 修改 app/javascript/app.js 修改ip地址和端口号 否则不能正常运行 vim app/javascript/app.js window.web3 = new Web3(new Web3.providers.HttpProvider("http://192.168.1.12:8545"));//这是老师的,IP和第13步一样;端口号改成8545。 window.web3 = new Web3(new Web3.providers.HttpProvider("http://127.0.0.1:8545"));//这是我的。 启动 npm run dev 在浏览器地址栏输入127.0.0.1:8008,打开web前端。可以看到当前有10000个Meta币。给刚才复制的账号转88个币,输入88,粘贴地址,点击Send MetaCoin。之后,余额少了88个币。再回到测试网络,可以看到,区块号增加了1。 演示结束。 Ctrl + Z:停止左边的 web 服务,Ctrl + B,→:切换到右边窗口,Ctrl + C:停止测试网络。exit:关闭一个tmux窗口,退出 tmux,退出默认的终端,都是这个命令。小结一下,本节简要介绍了Truffle的技术特性,演示了Truffle的安装过程,并运行了一个简单的实例。不足之处,请批评指正。


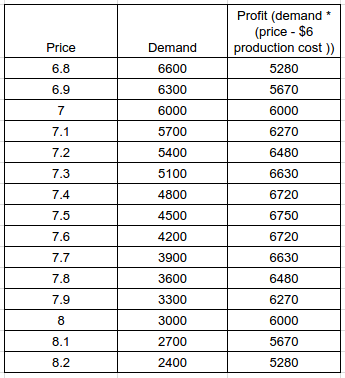
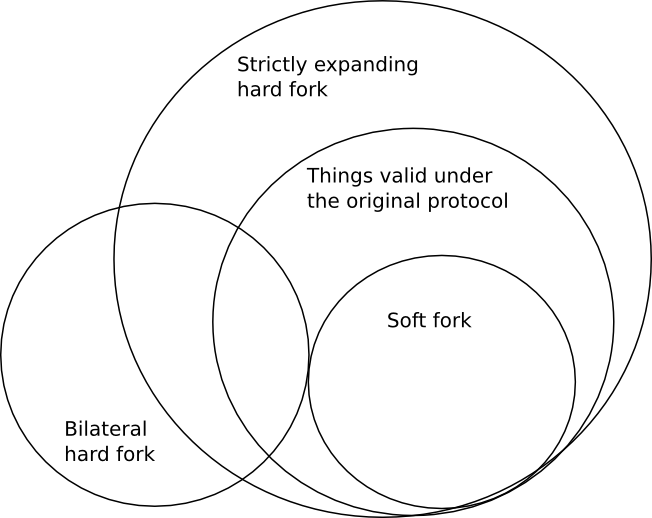
![[Mirror] Zk-SNARKs: Under the Hood](https://cdn-images-1.medium.com/max/2000/1*xX1YSBNSFjmkNKR2kP-TFA.png)
![[Mirror] Exploring Elliptic Curve Pairings](https://cdn-images-1.medium.com/max/2000/1*2PxXNwMceh1XC_waAP9NiA.jpeg)
![[Mirror] Quadratic Arithmetic Programs: from Zero to Hero](https://cdn-images-1.medium.com/max/2000/1*YD-ckgBfmmmRBCyVlhp8YQ.png)

