heyuan 发布的文章 - 六币之门

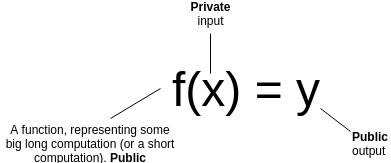
STARKs, Part I: Proofs with Polynomials STARKs, Part I: Proofs with Polynomials2017 Nov 09 See all posts STARKs, Part I: Proofs with Polynomials Special thanks to Eli Ben-Sasson for ongoing help, explanations and review, coming up with some of the examples used in this post, and most crucially of all inventing a lot of this stuff; thanks to Hsiao-wei Wang for reviewingHopefully many people by now have heard of ZK-SNARKs, the general-purpose succinct zero knowledge proof technology that can be used for all sorts of usecases ranging from verifiable computation to privacy-preserving cryptocurrency. What you might not know is that ZK-SNARKs have a newer, shinier cousin: ZK-STARKs. With the T standing for "transparent", ZK-STARKs resolve one of the primary weaknesses of ZK-SNARKs, its reliance on a "trusted setup". They also come with much simpler cryptographic assumptions, avoiding the need for elliptic curves, pairings and the knowledge-of-exponent assumption and instead relying purely on hashes and information theory; this also means that they are secure even against attackers with quantum computers.However, this comes at a cost: the size of a proof goes up from 288 bytes to a few hundred kilobytes. Sometimes the cost will not be worth it, but at other times, particularly in the context of public blockchain applications where the need for trust minimization is high, it may well be. And if elliptic curves break or quantum computers do come around, it definitely will be.So how does this other kind of zero knowledge proof work? First of all, let us review what a general-purpose succinct ZKP does. Suppose that you have a (public) function \(f\), a (private) input \(x\) and a (public) output \(y\). You want to prove that you know an \(x\) such that \(f(x) = y\), without revealing what \(x\) is. Furthermore, for the proof to be succinct, you want it to be verifiable much more quickly than computing \(f\) itself. Let's go through a few examples:\(f\) is a computation that takes two weeks to run on a regular computer, but two hours on a data center. You send the data center the computation (ie. the code to run \(f\) ), the data center runs it, and gives back the answer \(y\) with a proof. You verify the proof in a few milliseconds, and are convinced that \(y\) actually is the answer. You have an encrypted transaction, of the form "\(X_1\) was my old balance. \(X_2\) was your old balance. \(X_3\) is my new balance. \(X_4\) is your new balance". You want to create a proof that this transaction is valid (specifically, old and new balances are non-negative, and the decrease in my balance cancels out the increase in your balance). \(x\) can be the pair of encryption keys, and \(f\) can be a function which contains as a built-in public input the transaction, takes as input the keys, decrypts the transaction, performs the check, and returns 1 if it passes and 0 if it does not. \(y\) would of course be 1. You have a blockchain like Ethereum, and you download the most recent block. You want a proof that this block is valid, and that this block is at the tip of a chain where every block in the chain is valid. You ask an existing full node to provide such a proof. \(x\) is the entire blockchain (yes, all ?? gigabytes of it), \(f\) is a function that processes it block by block, verifies the validity and outputs the hash of the last block, and \(y\) is the hash of the block you just downloaded. So what's so hard about all this? As it turns out, the zero knowledge (ie. privacy) guarantee is (relatively!) easy to provide; there are a bunch of ways to convert any computation into an instance of something like the three color graph problem, where a three-coloring of the graph corresponds to a solution of the original problem, and then use a traditional zero knowledge proof protocol to prove that you have a valid graph coloring without revealing what it is. This excellent post by Matthew Green from 2014 describes this in some detail.The much harder thing to provide is succinctness. Intuitively speaking, proving things about computation succinctly is hard because computation is incredibly fragile. If you have a long and complex computation, and you as an evil genie have the ability to flip a 0 to a 1 anywhere in the middle of the computation, then in many cases even one flipped bit will be enough to make the computation give a completely different result. Hence, it's hard to see how you can do something like randomly sampling a computation trace in order to gauge its correctness, as it's just too easy to miss that "one evil bit". However, with some fancy math, it turns out that you can.The general very high level intuition is that the protocols that accomplish this use similar math to what is used in erasure coding, which is frequently used to make data fault-tolerant. If you have a piece of data, and you encode the data as a line, then you can pick out four points on the line. Any two of those four points are enough to reconstruct the original line, and therefore also give you the other two points. Furthermore, if you make even the slightest change to the data, then it is guaranteed at least three of those four points. You can also encode the data as a degree-1,000,000 polynomial, and pick out 2,000,000 points on the polynomial; any 1,000,001 of those points will recover the original data and therefore the other points, and any deviation in the original data will change at least 1,000,000 points. The algorithms shown here will make heavy use of polynomials in this way for error amplification. Changing even one point in the original data will lead to large changes in a polynomial's trajectoryA Somewhat Simple ExampleSuppose that you want to prove that you have a polynomial \(P\) such that \(P(x)\) is an integer with \(0 \leq P(x) \leq 9\) for all \(x\) from 1 to 1 million. This is a simple instance of the fairly common task of "range checking"; you might imagine this kind of check being used to verify, for example, that a set of account balances is still positive after applying some set of transactions. If it were \(1 \leq P(x) \leq 9\), this could be part of checking that the values form a correct Sudoku solution.The "traditional" way to prove this would be to just show all 1,000,000 points, and verify it by checking the values. However, we want to see if we can make a proof that can be verified in less than 1,000,000 steps. Simply randomly checking evaluations of \(P\) won't do; there's always the possibility that a malicious prover came up with a \(P\) which satisfies the constraint in 999,999 places but does not satisfy it in the last one, and random sampling only a few values will almost always miss that value. So what can we do? Let's mathematically transform the problem somewhat. Let \(C(x)\) be a constraint checking polynomial; \(C(x) = 0\) if \(0 \leq x \leq 9\) and is nonzero otherwise. There's a simple way to construct \(C(x)\): \(x \cdot (x-1) \cdot (x-2) \cdot \ldots(x-9)\) (we'll assume all of our polynomials and other values use exclusively integers, so we don't need to worry about numbers in between). Now, the problem becomes: prove that you know \(P\) such that \(C(P(x)) = 0\) for all \(x\) from 1 to 1,000,000. Let \(Z(x) = (x-1) \cdot (x-2) \cdot \ldots (x-1000000)\). It's a known mathematical fact that any polynomial which equals zero at all \(x\) from 1 to 1,000,000 is a multiple of \(Z(x)\). Hence, the problem can now be transformed again: prove that you know \(P\) and \(D\) such that \(C(P(x)) = Z(x) \cdot D(x)\) for all \(x\) (note that if you know a suitable \(C(P(x))\) then dividing it by \(Z(x)\) to compute \(D(x)\) is not too difficult; you can use long polynomial division or more realistically a faster algorithm based on FFTs). Now, we've converted our original statement into something that looks mathematically clean and possibly quite provable.So how does one prove this claim? We can imagine the proof process as a three-step communication between a prover and a verifier: the prover sends some information, then the verifier sends some requests, then the prover sends some more information. First, the prover commits to (ie. makes a Merkle tree and sends the verifier the root hash of) the evaluations of \(P(x)\) and \(D(x)\) for all \(x\) from 1 to 1 billion (yes, billion). This includes the 1 million points where \(0 \leq P(x) \leq 9\) as well as the 999 million points where that (probably) is not the case. We assume the verifier already knows the evaluation of \(Z(x)\) at all of these points; the \(Z(x)\) is like a "public verification key" for this scheme that everyone must know ahead of time (clients that do not have the space to store \(Z(x)\) in its entirety can simply store the Merkle root of \(Z(x)\) and require the prover to also provide branches for every \(Z(x)\) value that the verifier needs to query; alternatively, there are some number fields over which \(Z(x)\) for certain \(x\) is very easy to calculate). After receiving the commitment (ie. Merkle root) the verifier then selects a random 16 \(x\) values between 1 and 1 billion, and asks the prover to provide the Merkle branches for \(P(x)\) and \(D(x)\) there. The prover provides these values, and the verifier checks that (i) the branches match the Merkle root that was provided earlier, and (ii) \(C(P(x))\) actually equals \(Z(x) \cdot D(x)\) in all 16 cases. We know that this proof perfect completeness - if you actually know a suitable \(P(x)\), then if you calculate \(D(x)\) and construct the proof correctly it will always pass all 16 checks. But what about soundness - that is, if a malicious prover provides a bad \(P(x)\), what is the minimum probability that they will get caught? We can analyze as follows. Because \(C(P(x))\) is a degree-10 polynomial composed with a degree-1,000,000 polynomial, its degree will be at most 10,000,000. In general, we know that two different degree-\(N\) polynomials agree on at most \(N\) points; hence, a degree-10,000,000 polynomial which is not equal to any polynomial which always equals \(Z(x) \cdot D(x)\) for some \(x\) will necessarily disagree with them all at at least 990,000,000 points. Hence, the probability that a bad \(P(x)\) will get caught in even one round is already 99%; with 16 checks, the probability of getting caught goes up to \(1 - 10^\); that is to say, the scheme is about as hard to spoof as it is to compute a hash collision.So... what did we just do? We used polynomials to "boost" the error in any bad solution, so that any incorrect solution to the original problem, which would have required a million checks to find directly, turns into a solution to the verification protocol that can get flagged as erroneous at 99% of the time with even a single check.We can convert this three-step mechanism into a non-interactive proof, which can be broadcasted by a single prover once and then verified by anyone, using the Fiat-Shamir heuristic. The prover first builds up a Merkle tree of the \(P(x)\) and \(D(x)\) values, and computes the root hash of the tree. The root itself is then used as the source of entropy that determines what branches of the tree the prover needs to provide. The prover then broadcasts the Merkle root and the branches together as the proof. The computation is all done on the prover side; the process of computing the Merkle root from the data, and then using that to select the branches that get audited, effectively substitutes the need for an interactive verifier.The only thing a malicious prover without a valid \(P(x)\) can do is try to make a valid proof over and over again until eventually they get extremely lucky with the branches that a Merkle root that they compute selects, but with a soundness of \(1 - 10^\) (ie. probability of at least \(1 - 10^\) that a given attempted fake proof will fail the check) it would take a malicious prover billions of years to make a passable proof. Going FurtherTo illustrate the power of this technique, let's use it to do something a little less trivial: prove that you know the millionth Fibonacci number. To accomplish this, we'll prove that you have knowledge of a polynomial which represents a computation tape, with \(P(x)\) representing the \(x\)th Fibonacci number. The constraint checking polynomial will now hop across three x-coordinates: \(C(x_1, x_2, x_3) = x_3-x_2-x_1\) (notice how if \(C(P(x), P(x+1), P(x+2)) = 0\) for all \(x\) then \(P(x)\) represents a Fibonacci sequence). The translated problem becomes: prove that you know \(P\) and \(D\) such that \(C(P(x), P(x+1), P(x+2)) = Z(x) \cdot D(x)\). For each of the 16 indices that the proof audits, the prover will need to provide Merkle branches for \(P(x)\), \(P(x+1)\), \(P(x+2)\) and \(D(x)\). The prover will additionally need to provide Merkle branches to show that \(P(0) = P(1) = 1\). Otherwise, the entire process is the same.Now, to accomplish this in reality there are two problems that need to be resolved. The first problem is that if we actually try to work with regular numbers the solution would not be efficient in practice, because the numbers themselves very easily get extremely large. The millionth Fibonacci number, for example, has 208988 digits. If we actually want to achieve succinctness in practice, instead of doing these polynomials with regular numbers, we need to use finite fields - number systems that still follow the same arithmetic laws we know and love, like \(a \cdot (b+c) = (a\cdot b) + (a\cdot c)\) and \((a^2 - b^2) = (a-b) \cdot (a+b)\), but where each number is guaranteed to take up a constant amount of space. Proving claims about the millionth Fibonacci number would then require a more complicated design that implements big-number arithmetic on top of this finite field math.The simplest possible finite field is modular arithmetic; that is, replace every instance of \(a + b\) with \(a + b \mod\) for some prime \(N\), do the same for subtraction and multiplication, and for division use modular inverses (eg. if \(N = 7\), then \(3 + 4 = 0\), \(2 + 6 = 1\), \(3 \cdot 4 = 5\), \(4 / 2 = 2\) and \(5 / 2 = 6\)). You can learn more about these kinds of number systems from my description on prime fields here (search "prime field" in the page) or this Wikipedia article on modular arithmetic (the articles that you'll find by searching directly for "finite fields" and "prime fields" unfortunately tend to be very complicated and go straight into abstract algebra, don't bother with those).Second, you might have noticed that in my above proof sketch for soundness I neglected to cover one kind of attack: what if, instead of a plausible degree-1,000,000 \(P(x)\) and degree-9,000,000 \(D(x)\), the attacker commits to some values that are not on any such relatively-low-degree polynomial? Then, the argument that an invalid \(C(P(x))\) must differ from any valid \(C(P(x))\) on at least 990 million points does not apply, and so different and much more effective kinds of attacks are possible. For example, an attacker could generate a random value \(p\) for every \(x\), then compute \(d = C(p) / Z(x)\) and commit to these values in place of \(P(x)\) and \(D(x)\). These values would not be on any kind of low-degree polynomial, but they would pass the test.It turns out that this possibility can be effectively defended against, though the tools for doing so are fairly complex, and so you can quite legitimately say that they make up the bulk of the mathematical innovation in STARKs. Also, the solution has a limitation: you can weed out commitments to data that are very far from any degree-1,000,000 polynomial (eg. you would need to change 20% of all the values to make it a degree-1,000,000 polynomial), but you cannot weed out commitments to data that only differ from a polynomial in only one or two coordinates. Hence, what these tools will provide is proof of proximity - proof that most of the points on \(P\) and \(D\) correspond to the right kind of polynomial.As it turns out, this is sufficient to make a proof, though there are two "catches". First, the verifier needs to check a few more indices to make up for the additional room for error that this limitation introduces. Second, if we are doing "boundary constraint checking" (eg. verifying \(P(0) = P(1) = 1\) in the Fibonacci example above), then we need to extend the proof of proximity to not only prove that most points are on the same polynomial, but also prove that those two specific points (or whatever other number of specific points you want to check) are on that polynomial.In the next part of this series, I will describe the solution to proximity checking in much more detail, and in the third part I will describe how more complex constraint functions can be constructed to check not just Fibonacci numbers and ranges, but also arbitrary computation.

On Medium-of-Exchange Token Valuations On Medium-of-Exchange Token Valuations2017 Oct 17 See all posts On Medium-of-Exchange Token Valuations One kind of token model that has become popular among many recent token sale projects is the "network medium of exchange token". The general pitch for this kind of token goes as follows. We, the developers, build a network, and this network allows you to do new cool stuff. This network is a sharing-economy-style system: it consists purely of a set of sellers, that provide resources within some protocol, and buyers that purchase the services, where both buyers and sellers come from the community. But the purchase and sale of things within this network must be done with the new token that we're selling, and this is why the token will have value.If it were the developers themselves that were acting as the seller, then this would be a very reasonable and normal arrangement, very similar in nature to a Kickstarter-style product sale. The token actually would, in a meaningful economic sense, be backed by the services that are provided by the developers.We can see this in more detail by describing what is going on in a simple economic model. Suppose that \(N\) people value a product that a developer wants to release at \(\$x\), and believe the developer will give them the product. The developer does a sale, and raises \(N\) units for \(\$w < x\) each, thus raising a total revenue of \(\$Nw\). The developer builds the product, and gives it to each of the buyers. At the end of the day, the buyers are happy, and the developer is happy. Nobody feels like they made an avoidable mistake in participating, and everyone's expectations have been met. This kind of economic model is clearly stable.Now, let's look at the story with a "medium of exchange" token. \(N\) people value a product that will exist in a decentralized network at \(\$x\); the product will be sold at a price of \(\$w < x\). They each buy \(\$w\) of tokens in the sale. The developer builds the network. Some sellers come in, and offer the product inside the network for \(\$w\). The buyers use their tokens to purchase this product, spending \(\$w\) of tokens and getting \(\$x\) of value. The sellers spend \(\$v < w\) of resources and effort producing this product, and they now have \(\$w\) worth of tokens.Notice that here, the cycle is not complete, and in fact it never will be; there needs to be an ongoing stream of buyers and sellers for the token to continue having its value. The stream does not strictly speaking have to be endless; if in every round there is a chance of at least \(\frac\) that there will be a next round, then the model still works, as even though someone will eventually be cheated, the risk of any individual participant becoming that person is lower than the benefit that they get from participating. It's also totally possible that the token would depreciate in each round, with its value multiplying by some factor \(f\) where \(\frac < f < 1\), until it eventually reaches a price of zero, and it would still be on net in everyone's interest to participate. Hence, the model is theoretically feasible, but you can see how this model is more complex and more tenuous than the simple "developers as seller" model.Traditional macroeconomics has a simple equation to try to value a medium of exchange:\(MV = PT\)Here:\(M\) is the total money supply; that is, the total number of coins \(V\) is the "velocity of money"; that is, the number of times that an average coin changes hands every day \(P\) is the "price level". This is the price of goods and services in terms of the token; so it is actually the inverse of the currency's price \(T\) is the transaction volume: the economic value of transactions per day The proof for this is a trivial equality: if there are \(N\) coins, and each changes hands \(M\) times per day, then this is \(M \cdot N\) coins' worth of economic value transacted per day. If this represents \(\$T\) worth of economic value, then the price of each coin is \(\frac\), so the "price level" is the inverse of this, \(\frac\).For easier analysis, we can recast two variables:We refer to \(\frac\) with \(H\), the time that a user holds a coin before using it to make a transaction We refer to \(\frac\) with \(C\), the price of the currency (think \(C = cost\)) Now, we have:\(\frac = \frac\)\(MC = TH\)The left term is quite simply the market cap. The right term is the economic value transacted per day, multiplied by the amount of time that a user holds a coin before using it to transact.This is a steady-state model, assuming that the same quantity of users will also be there. In reality, however, the quantity of users may change, and so the price may change. The time that users hold a coin may change, and this may cause the price to change as well.Let us now look once again at the economic effect on the users. What do users lose by using an application with a built-in appcoin rather than plain old ether (or bitcoin, or USD)? The simplest way to express this is as follows: the "implicit cost" imposed by such a system on users the cost to the user of holding those coins for that period of time, instead of holding that value in the currency that they would otherwise have preferred to hold.There are many factors involved in this cost: cognitive costs, exchange costs and spreads, transaction fees, and many smaller items. One particular significant factor of this implicit cost is expected return. If a user expects the appcoin to only grow in value by 1% per year, while their other available alternatives grow 3% per year, and they hold $20 of the currency for five days, then that is an expected loss of roughly \(\$20 \cdot 2% \cdot 5 / 365 = \$0.0054\).One immediate conclusion from this particular insight is that appcoins are very much a multi-equilibrium game. If the appcoin grows at 2% per year, then the fee drops to $0.0027, and this essentially makes the "de-facto fee" of the application (or at least a large component of it) 2x cheaper, attracting more users and growing its value more. If the appcoin starts falling at 10% per year, however, then the "de-facto fee" grows to $0.035, driving many users away and accelerating its growth.This leads to increased opportunities for market manipulation, as a manipulator would not just be wasting their money fighting against a single equilibrium, but may in fact successfully nudge a given currency from one equilibrium into another, and profit from successfully "predicting" (ie. causing) this shift. It also means there is a large amount of path dependency, and established brands matter a lot; witness the epic battles over which fork of the bitcoin blockchain can be called Bitcoin for one particular high-profile example.Another, and perhaps even more important, conclusion is that the market cap of an appcoin depends crucially on the holding time \(H\). If someone creates a very efficient exchange, which allows users to purchase an appcoin in real time and then immediately use it in the application, then allowing sellers to immediately cash out, then the market cap would drop precipitously. If a currency is stable or prospects are looking optimistic, then this may not matter because users actually see no disadvantage from holding the token instead of holding something else (ie. zero "de-facto fee"), but if prospects start to turn sour then such a well-functioning exchange can acelerate its demise.You might think that exchanges are inherently inefficient, requiring users to create an account, login, deposit coins, wait for 36 confirmations, trade and logout, but in fact hyper-efficient exchanges are around the corner. Here is a thread discussing designs for fully autonomous synchronous on-chain transactions, which can convert token A into token B, and possibly even then use token B to do something, within a single transaction. Many other platforms are being developed as well.What this all serves to show is that relying purely on the medium-of-exchange argument to support a token value, while attractive because of its seeming ability to print money out of thin air, is ultimately quite brittle. Protocol tokens using this model may well be sustained for some time due to irrationality and temporary equilibria where the implicit cost of holding the token is zero, but it is a kind of model which always has an unavoidable risk of collapsing at any time.So what is the alternative? One simple alternative is the etherdelta approach, where an application simply collects fees in the interface. One common criticism is: but can't someone fork the interface to take out the fees? A counter-retort is: someone can also fork the interface to replace your protocol token with ETH, BTC, DOGE or whatever else users would prefer to use. One can make a more sophisticated argument that this is hard because the "pirate" version would have to compete with the "official" version for network effect, but one can just as easily create an official fee-paying client that refuses to interact with non-fee-paying clients as well; this kind of network effect-based enforcement is similar to how value-added-taxes are typically enforced in Europe and other places. Official-client buyers would not interact with non-official-client sellers, and official-client sellers would not interact with non-official-client buyers, so a large group of users would need to switch to the "pirate" client at the same time to successfully dodge fees. This is not perfectly robust, but it is certainly as good as the approach of creating a new protocol token.If developers want to front-load revenue to fund initial development, then they can sell a token, with the property that all fees paid are used to buy back some of the token and burn it; this would make the token backed by the future expected value of upcoming fees spent inside the system. One can transform this design into a more direct utility token by requiring users to use the utility token to pay fees, and having the interface use an exchange to automatically purchase tokens if the user does not have tokens already.The important thing is that for the token to have a stable value, it is highly beneficial for the token supply to have sinks - places where tokens actually disappear and so the total token quantity decreases over time. This way, there is a more transparent and explicit fee paid by users, instead of the highly variable and difficult to calculate "de-facto fee", and there is also a more transparent and explicit way to figure out what the value of protocol tokens should be.

A Prehistory of the Ethereum Protocol A Prehistory of the Ethereum Protocol2017 Sep 14 See all posts A Prehistory of the Ethereum Protocol Although the ideas behind the current Ethereum protocol have largely been stable for two years, Ethereum did not emerge all at once, in its current conception and fully formed. Before the blockchain has launched, the protocol went through a number of significant evolutions and design decisions. The purpose of this article will be to go through the various evolutions that the protocol went through from start to launch; the countless work that was done on the implementations of the protocol such as Geth, cppethereum, pyethereum, and EthereumJ, as well as the history of applications and businesses in the Ethereum ecosystem, is deliberately out of scope.Also out of scope is the history of Casper and sharding research. While we can certainly make more blog posts talking about all of the various ideas Vlad, Gavin, myself and others came up with, and discarded, including "proof of proof of work", hub-and-spoke chains, "hypercubes", shadow chains (arguably a precursor to Plasma), chain fibers, and various iterations of Casper, as well as Vlad's rapidly evolving thoughts on reasoning about incentives of actors in consensus protocols and properties thereof, this would also be far too complex a story to go through in one post, so we will leave it out for now.Let us first begin with the very earliest version of what would eventually become Ethereum, back when it was not even called Ethereum. When I was visiting Israel in October 2013, I spent quite a bit of time with the Mastercoin team, and even suggested a few features for them. After spending a couple of times thinking about what they were doing, I sent the team a proposal to make their protocol more generalized and support more types of contracts without adding an equally large and complex set of features:https://web.archive.org/web/20150627031414/http://vbuterin.com/ultimatescripting.htmlNotice that this is very far from the later and more expansive vision of Ethereum: it specialized purely in what Mastercoin was trying to specialize in already, namely two-party contracts where parties A and B would both put in money, and then they would later get money out according to some formula specified in the contract (eg. a bet would say "if X happens then give all the money to A, otherwise give all the money to B"). The scripting language was not Turing-complete.The Mastercoin team was impressed, but they were not interested in dropping everything they were doing to go in this direction, which I was increasingly convinced is the correct choice. So here comes version 2, circa December:https://web.archive.org/web/20131219030753/http://vitalik.ca/ethereum.htmlHere you can see the results of a substantial rearchitecting, largely a result of a long walk through San Francisco I took in November once I realized that smart contracts could potentially be fully generalized. Instead of the scripting language being simply a way of describing the terms of relations between two parties, contracts were themselves fully-fledged accounts, and had the ability to hold, send and receive assets, and even maintain a permanent storage (back then, the permanent storage was called "memory", and the only temporary "memory" was the 256 registers). The language switched from being a stack-based machine to being a register-based one on my own volition; I had little argument for this other than that it seemed more sophisticated.Additionally, notice that there is now a built-in fee mechanism:At this point, ether literally was gas; after every single computational step, the balance of the contract that a transaction was calling would drop a little bit, and if the contract ran out of money execution would halt. Note that this "receiver pays" mechanism meant that the contract itself had to require the sender to pay the contract a fee, and immediately exit if this fee is not present; the protocol allocated an allowance of 16 free execution steps to allow contracts to reject non-fee-paying transactions.This was the time when the Ethereum protocol was entirely my own creation. From here on, however, new participants started to join the fold. By far the most prominent on the protocol side was Gavin Wood, who reached out to me in an about.me message in December 2013:Jeffrey Wilcke, lead developer of the Go client (back then called "ethereal") also reached out and started coding around the same time, though his contributions were much more on the side of client development rather than protocol research. "Hey Jeremy, glad to see you're interested in Ethereum..." Gavin's initial contributions were two-fold. First, you might notice that the contract calling model in the initial design was an asynchronous one: although contract A could create an "internal transaction" to contract B ("internal transaction" is Etherscan's lingo; initially they were just called "transactions" and then later "message calls" or "calls"), the internal transaction's execution would not start until the execution of the first transaction completely finished. This meant that transactions could not use internal transactions as a way of getting information from other contracts; the only way to do that was the EXTRO opcode (kind of like an SLOAD that you could use to read other contracts' storage), and this too was later removed with the support of Gavin and others.When implementing my initial spec, Gavin naturally implemented internal transactions synchronously without even realizing that the intent was different - that is to say, in Gavin's implementation, when a contract calls another contract, the internal transaction gets executed immediately, and once that execution finishes, the VM returns back to the contract that created the internal transaction and proceeds to the next opcode. This approach seemed to both of us to be superior, so we decided to make it part of the spec.Second, a discussion between him and myself (during a walk in San Francisco, so the exact details will be forever lost to the winds of history and possibly a copy or two in the deep archives of the NSA) led to a re-factoring of the transaction fee model, moving away from the "contract pays" approach to a "sender pays" approach, and also switching to the "gas" architecture. Instead of each individual transaction step immediately taking away a bit of ether, the transaction sender pays for and is allocated some "gas" (roughly, a counter of computational steps), and computational steps drew from this allowance of gas. If a transaction runs out of gas, the gas would still be forfeit, but the entire execution would be reverted; this seemed like the safest thing to do, as it removed an entire class of "partial execution" attacks that contracts previously had to worry about. When a transaction execution finishes, the fee for any unused gas is refunded.Gavin can also be largely credited for the subtle change in vision from viewing Ethereum as a platform for building programmable money, with blockchain-based contracts that can hold digital assets and transfer them according to pre-set rules, to a general-purpose computing platform. This started with subtle changes in emphasis and terminology, and later this influence became stronger with the increasing emphasis on the "Web 3" ensemble, which saw Ethereum as being one piece of a suite of decentralized technologies, the other two being Whisper and Swarm.There were also changes made around the start of 2014 that were suggested by others. We ended up moving back to a stack-based architecture after the idea was suggested by Andrew Miller and others.Charles Hoskinson suggested the switch from Bitcoin's SHA256 to the newer SHA3 (or, more accurately, keccak256). Although there was some controversy for a while, discussions with Gavin, Andrew and others led to establishing that the size of values on the stack should be limited to 32 bytes; the other alternative being considered, unlimited-size integers, had the problem that it was too difficult to figure out how much gas to charge for additions, multiplications and other operations.The initial mining algorithm that we had in mind, back in January 2014, was a contraption called Dagger:https://github.com/ethereum/wiki/blob/master/Dagger.mdDagger was named after the "directed acyclic graph" (DAG), the mathematical structure that is used in the algorithm. The idea is that every N blocks, a new DAG would be pseudorandomly generated from a seed, and the bottom layer of the DAG would be a collection of nodes that takes several gigabytes to store. However, generating any individual value in the DAG would require calculating only a few thousand entries. A "Dagger computation" involved getting some number of values in random positions in this bottom-level dataset and hashing them together. This meant that there was a fast way to make a Dagger calculation - already having the data in memory, and a slow, but not memory intensive way - regenerating each value from the DAG that you need to get from scratch.The intention of this algorithm was to have the same "memory-hardness" properties as algorithms that were popular at the time, like Scrypt, but still be light-client friendly. Miners would use the fast way, and so their mining would be constrained by memory bandwidth (the theory is that consumer-grade RAM is already very heavily optimized, and so it would be hard to further optimize it with ASICs), but light clients could use the memory-free but slower version for verification. The fast way might take a few microseconds and the slow but memory-free way a few milliseconds, so it would still be very viable for light clients.From here, the algorithm would change several times over the course of Ethereum development. The next idea that we went through is "adaptive proof of work"; here, the proof of work would involve executing randomly selected Ethereum contracts, and there is a clever reason why this is expected to be ASIC-resistant: if an ASIC was developed, competing miners would have the incentive to create and publish many contracts that that ASIC was not good at executing. There is no such thing as an ASIC for general computation, the story goes, as that is just a CPU, so we could instead use this kind of adversarial incentive mechanism to make a proof of work that essentially was executing general computation.This fell apart for one simple reason: long-range attacks. An attacker could start a chain from block 1, fill it up with only simple contracts that they can create specialized hardware for, and rapidly overtake the main chain. So... back to the drawing board.The next algorithm was something called Random Circuit, described in this google doc here, proposed by myself and Vlad Zamfir, and analyzed by Matthew Wampler-Doty and others. The idea here was also to simulate general-purpose computation inside a mining algorithm, this time by executing randomly generated circuits. There's no hard proof that something based on these principles could not work, but the computer hardware experts that we reached out to in 2014 tended to be fairly pessimistic on it. Matthew Wampler-Doty himself suggested a proof of work based on SAT solving, but this too was ultimately rejected.Finally, we came full circle with an algorithm called "Dagger Hashimoto". "Dashimoto", as it was sometimes called in short, borrowed many ideas from Hashimoto, a proof of work algorithm by Thaddeus Dryja that pioneered the notion of "I/O bound proof of work", where the dominant limiting factor in mining speed was not hashes per second, but rather megabytes per second of RAM access. However, it combined this with Dagger's notion of light-client-friendly DAG-generated datasets. After many rounds of tweaking by myself, Matthew, Tim and others, the ideas finally converged into the algorithm we now call Ethash.By the summer of 2014, the protocol had considerably stabilized, with the major exception of the proof of work algorithm which would not reach the Ethash phase until around the beginning of 2015, and a semi-formal specification existed in the form of Gavin's yellow paper.In August 2014, I developed and introduced the uncle mechanism, which allows Ethereum's blockchain to have a shorter block time and higher capacity while mitigating centralization risks. This was introduced as part of PoC6.Discussions with the Bitshares team led us to consider adding heaps as a first-class data structure, though we ended up not doing this due to lack of time, and later security audits and DoS attacks will show that it is actually much harder than we had thought at the time to do this safely.In September, Gavin and I planned out the next two major changes to the protocol design. First, alongside the state tree and transaction tree, every block would also contain a "receipt tree". The receipt tree would include hashes of the logs created by a transaction, along with intermediate state roots. Logs would allow transactions to create "outputs" that are saved in the blockchain, and are accessible to light clients, but that are not accessible to future state calculations. This could be used to allow decentralized applications to easily query for events, such as token transfers, purchases, exchange orders being created and filled, auctions being started, and so forth.There were other ideas that were considered, like making a Merkle tree out of the entire execution trace of a transaction to allow anything to be proven; logs were chosen because they were a compromise between simplicity and completeness.The second was the idea of "precompiles", solving the problem of allowing complex cryptographic computations to be usable in the EVM without having to deal with EVM overhead. We had also gone through many more ambitious ideas about "native contracts", where if miners have an optimized implementation of some contracts they could "vote" the gasprice of those contracts down, so contracts that most miners could execute much more quickly would naturally have a lower gas price; however, all of these ideas were rejected because we could not come up with a cryptoeconomically safe way to implement such a thing. An attacker could always create a contract which executes some trapdoored cryptographic operation, distribute the trapdoor to themselves and their friends to allow them to execute this contract much faster, then vote the gasprice down and use this to DoS the network. Instead we opted for the much less ambitious approach of having a smaller number of precompiles that are simply specified in the protocol, for common operations such as hashes and signature schemes.Gavin was also a key initial voice in developing the idea of "protocol abstraction" - moving as many parts of the protocol such as ether balances, transaction signing algorithms, nonces, etc into the protocol itself as contracts, with a theoretical final goal of reaching a situation where the entire ethereum protocol could be described as making a function call into a virtual machine that has some pre-initialized state. There was not enough time for these ideas to get into the initial Frontier release, but the principles are expected to start slowly getting integrated through some of the Constantinople changes, the Casper contract and the sharding specification.This was all implemented in PoC7; after PoC7, the protocol did not really change much, with the exception of minor, though in some cases important, details that would come out through security audits...In early 2015, came the pre-launch security audits organized by Jutta Steiner and others, which included both software code audits and academic audits. The software audits were primarily on the C++ and Go implementations, which were led by Gavin Wood and Jeffrey Wilcke, respectively, though there was also a smaller audit on my pyethereum implementation. Of the two academic audits, one was performed by Ittay Eyal (of "selfish mining" fame), and the other by Andrew Miller and others from Least Authority. The Eyal audit led to a minor protocol change: the total difficulty of a chain would not include uncles. The Least Authority audit was more focused on smart contract and gas economics, as well as the Patricia tree. This audit led to several protocol changes. One small one is the use of sha3(addr) and sha3(key) as trie keys instead of the address and key directly; this would make it harder to perform a worst-case attack on the trie. And a warning that was perhaps a bit too far ahead of its time... Another significant thing that we discussed was the gas limit voting mechanism. At the time, we were already concerned by perceived lack of progress in the bitcoin block size debate, and wanted to have a more flexible design in Ethereum that could adjust over time as needed. But the challenge is: what is the optimal limit? My initial thought had been to make a dynamic limit, targeting \(1.5 \cdot\) the long-term exponential moving average of the actual gas usage, so that in the long run on average blocks would be \(\frac\) full. However, Andrew showed that this was exploitable in some ways - specifically, miners who wanted to raise the limit would simply include transactions in their own blocks that consume a very large amount of gas, but take very little time to process, and thereby always create full blocks at no cost to themselves. The security model was thus, at least in the upward direction, equivalent to simply having miners vote on the gas limit.We did not manage to come up with a gas limit strategy that was less likely to break, and so Andrew's recommended solution was to simply have miners vote on the gas limit explicitly, and have the default strategy for voting be the \(1.5\cdot\) EMA rule. The reasoning was that we were still very far from knowing the right approach for setting maximum gas limits, and the risk of any specific approach failing seemed greater than the risk of miners abusing their voting power. Hence, we might as well simply let miners vote on the gas limit, and accept the risk that the limit will go too high or too low, in exchange for the benefit of flexibility, and the ability for miners to work together to very quickly adjust the limit upwards or downwards as needed.After a mini-hackathon between Gavin, Jeff and myself, PoC9 was launched in March, and was intended to be the final proof of concept release. A testnet, Olympic, ran for four months, using the protocol that was intended to be used in the livenet, and Ethereum's long-term plan was established. Vinay Gupta wrote a blog post, "The Ethereum Launch Process", that described the four expected stages of Ethereum livenet development, and gave them their current names: Frontier, Homestead, Metropolis and Serenity.Olympic ran for four months. In the first two months, many bugs were found in the various implementations, consensus failures happened, among other issues, but around June the network noticeably stabilized. In July a decision was made to make a code-freeze, followed by a release, and on July 30 the release took place.

A Note on Metcalfe's Law, Externalities and Ecosystem Splits A Note on Metcalfe's Law, Externalities and Ecosystem Splits2017 Jul 27 See all posts A Note on Metcalfe's Law, Externalities and Ecosystem Splits Looks like it's blockchain split season again. For background of various people discussing the topic, and whether such splits are good or bad:Power laws and network effects (arguing the BTC/BCC split may destroy value due to network effect loss): https://medium.com/crypto-fundamental/power-laws-and-network-effects-why-bitcoincash-is-not-a-free-lunch-5adb579972aa Brian Armstrong on the Ethereum Hard Fork (last year): https://blog.coinbase.com/on-the-ethereum-hard-fork-780f1577e986 Phil Daian on the ETH/ETC split: http://pdaian.com/blog/stop-worrying-love-etc/ Given that ecosystem splits are not going away, and we may well see more of them in the crypto industry over the next decade, it seems useful to inform the discussion with some simple economic modeling. With that in mind, let's get right to it.Suppose that there exist two projects A and B, and a set of users of total size \(N\), where A has \(N_a\) users and B has \(N_b\) users. Both projects benefit from network effects, so they have a utility that increases with the number of users. However, users also have their own differing taste preferences, and this may lead them to choose the smaller platform over the bigger platform if it suits them better.We can model each individual's private utility in one of four ways:1. \(U(A) = p + N_a\) \(U(B) = q + N_b\) 2. \(U(A) = p \cdot N_a\) \(U(B) = q \cdot N_b\) 3. \(U(A) = p + \ln\) \(U(B) = q + \ln\) 4. \(U(A) = p \cdot \ln\)        \(U(B) = q \cdot \ln\) \(p\) and \(q\) are private per-user parameters that you can think of as corresponding to users' distinct preferences. The difference between the first two approaches and the last two reflects differences between interpretations of Metcalfe's law, or more broadly the idea that the per-user value of a system grows with the number of users. The original formulation suggested a per-user value of \(N\) (that is, a total network value of \(N^\)), but other analysis (see here) suggests that above very small scales \(N\log\) usually dominates; there is a controversy over which model is correct. The difference between the first and second (and between the third and fourth) is the extent to which utility from a system's intrinsic quality and utility from network effects are complementary - that is, are the two things good in completely separate ways that do not interact with each other, like social media and coconuts, or are network effects an important part of letting the intrinsic quality of a system shine?We can now analyze each case in turn by looking at a situation where \(N_a\) users choose A and \(N_b\) users choose B, and analyze each individual's decision to choose one or the other from the perspective of economic externalities - that is, does a user's choice to switch from A to B have a positive net effect on others' utility or a negative one? If switching has a positive externality, then it is virtuous and should be socially nudged or encouraged, and if it has a negative externality then it should be discouraged. We model an "ecosystem split" as a game where to start off \(N_a = N\) and \(N_b = 0\) and users are deciding for themselves whether or not to join the split, that is, to move from A to B, possibly causing \(N_a\) to fall and \(N_b\) to rise.Switching (or not switching) from A to B has externalties because A and B both have network effects; switching from A to B has the negative externality of reducing A's network effect, and so hurting all remaining A users, but it also has the positive externality of increasing B's network effect, and so benefiting all B users.Case 1Switching from A to B gives \(N_a\) users a negative externality of one, so a total loss of \(N_a\), and it gives \(N_b\) users a positive externality of one, so a total gain of \(N_b\). Hence, the total externality is of size \(N_b - N_a\); that is, switching from the smaller to the larger platform has positive externalities, and switching from the larger platform to the smaller platform has negative externalities.Case 2Suppose \(P_a\) is the sum of \(p\) values of \(N_a\) users, and \(Q_b\) is the sum of \(q\) values of \(N_b\) users. The total negative externality is \(P_a\) and the total positive externality is \(Q_b\). Hence, switching from the smaller platform to the larger has positive social externalities if the two platforms have equal intrinsic quality to their users (ie. users of A intrinsically enjoy A as much as users of B intrinsically enjoy B, so \(p\) and \(q\) values are evenly distributed), but if it is the case that A is bigger but B is better, then there are positive externalities in switching to B.Furthermore, notice that if a user is making a switch from a larger A to a smaller B, then this itself is revealed-preference evidence that, for that user, and for all existing users of B, \(\frac > \frac\). However, if the split stays as a split, and does not proceed to become a full-scale migration, then that means that users of A hold different views, though this could be for two reasons: (i) they intrinsically dislike A but not by enough to justify the switch, (ii) they intrinsically like A more than B. This could arise because (a) A users have a higher opinion of A than B users, or (b) A users have a lower opinion of B than B users. In general, we see that moving from a system that makes its average user less happy to a system that makes its average user more happy has positive externalities, and in other situations it's difficult to say.Case 3The derivative of \(\ln\) is \(\frac\). Hence, switching from A to B gives \(N_a\) users a negative externality of \(\frac\), and it gives \(N_b\) users a positive externality of \(\frac\). Hence, the negative and positive externalities are both of total size one, and thus cancel out. Hence, switching from one platform to the other imposes no social externalities, and it is socially optimal if all users switch from A to B if and only if they think that it is a good idea for them personally to do so.Case 4Let \(P_a\) and \(Q_b\) are before. The negative externality is of total size \(\frac\) and the positive externality is of total size \(\frac\). Hence, if the two systems have equal intrinsic quality, the externality is of size zero, but if one system has higher intrinsic quality, then it is virtuous to switch to it. Note that as in case 2, if users are switching from a larger system to a smaller system, then that means that they find the smaller system to have higher intrinsic quality, although, also as in case 2, if the split remains a split and does not become a full-scale migration, then that means other users see the intrinsic quality of the larger system as higher, or at least not lower by enough to be worth the network effects.The existence of users switching to B suggests that for them, \(\frac \geq \frac}}\), so for the \(\frac > \frac\) condition to not hold (ie. for a move from a larger system to a smaller system not to have positive externalities) it would need to be the case that users of A have similarly high values of \(p\) - an approximate heuristic is, the users of A would need to love A so much that if they were the ones in the minority that would be willing to split off and move to (or stay with) the smaller system. In general, it thus seems that moves from larger systems to smaller systems that actually do happen will have positive externalities, but it is far from ironclad that this is the case.Hence, if the first model is true, then to maximize social welfare we should be trying to nudge people to switch to (or stay with) larger systems over smaller systems, and splits should be discouraged. If the fourth model is true, then we should be at least slightly trying to nudge people to switch to smaller systems over larger systems, and splits should be slightly encouraged. If the third model is true, then people will choose the socially optimal thing all by themselves, and if the second model is true, it's a toss-up.It is my personal view that the truth lies somewhere between the third and fourth models, and the first and second greatly overstate network effects above small scales. The first and second model (the \(N^\) form of Metcalfe's law) essentially state that a system growing from 990 million to 1 billion users gives the same increase in per-user utility as growing from 100,000 to 10.1 million users, which seems very unrealistic, whereas the \(N\log\) model (growing from 100 million to 1 billion users gives the same increase in per-user utility as growing from 100,000 to 10 million users) intuitively seems much more correct.And the third model says: if you see people splitting off from a larger system to create a smaller system because they want something that more closely matches their personal values, then the fact that these people have already shown that they value this switch enough to give up the comforts of the original system's network effects is by itself enough evidence to show that the split is socially beneficial. Hence, unless I can be convinced that the first model is true, or that the second model is true and the specific distributions of \(p\) and \(q\) values make splits make negative negative externalities, I maintain my existing view that those splits that actually do happen (though likely not hypothetical splits that end up not happening due to lack of interest) are in the long term socially beneficial, value-generating events.

The Triangle of Harm The Triangle of Harm2017 Jul 16 See all posts The Triangle of Harm The following is a diagram from a slide that I made in one of my presentations at Cornell this week: If there was one diagram that could capture the core principle of Casper's incentivization philosophy, this might be it. Hence, it warrants some further explanation.The diagram shows three constituencies - the minority, the majority and the protocol (ie. users), and four arrows representing possible adversarial actions: the minority attacking the protocol, the minority attacking the majority, the majority attacking the protocol, and the majority attacking the minority. Examples of each include:Minority attacking the protocol - Finney attacks (an attack done by a miner on a proof of work blockchain where the miner double-spends unconfirmed, or possibly single-confirmed, transactions) Minority attacking the majority - feather forking (a minority in a proof of work chain attempting to revert any block that contains some undesired transactions, though giving up if the block gets two confirmations) Majority attacking the protocol - traditional 51% attacks Majority attacking the minority - a 51% censorship attack, where a cartel refuses to accept any blocks from miners (or validators) outside the cartel The essence of Casper's philosophy is this: for all four categories of attack, we want to put an upper bound on the ratio between the amount of harm suffered by the victims of the attack and the cost to the attacker. In some ways, every design decision in Casper flows out of this principle.This differs greatly from the usual proof of work incentivization school of thought in that in the proof of work view, the last two attacks are left undefended against. The first two attacks, Finney attacks and feather forking, are costly because the attacker risks their blocks not getting included into the chain and so loses revenue. If the attacker is a majority, however, the attack is costless, because the attacker can always guarantee that their chain will be the main chain. In the long run, difficulty adjustment ensures that the total revenue of all miners is exactly the same no matter what, and this further means that if an attack causes some victims to lose money, then the attacker gains money.This property of proof of work arises because traditional Nakamoto proof of work fundamentally punishes dissent - if you as a miner make a block that aligns with the consensus, you get rewarded, and if you make a block that does not align with the consensus you get penalized (the penalty is not in the protocol; rather, it comes from the fact that such a miner expends electricity and capital to produce the block and gets no reward).Casper, on the other hand, works primarily bypunishing equivocation- if you send two messages that conflict with each other, then you get very heavily penalized, even if one of those messages aligns with the consensus (read more on this in the blog post on "minimal slashing conditions"). Hence, in the event of a finality reversion attack, those who caused the reversion event are penalized, and everyone else is left untouched; the majority can attack the protocol only at heavy cost, and the majority cannot cause the minority to lose money.It gets more challenging when we move to talking about two other kinds of attacks - liveness faults, and censorship. A liveness fault is one where a large portion of Casper validators go offline, preventing the consensus from reaching finality, and a censorship fault is one where a majority of Casper validators refuse to accept some transactions, or refuse to accept consensus messages from other Casper validators (the victims) in order to deprive them of rewards.This touches on a fundamental dichotomy: speaker/listener fault equivalence. Suppose that person B says that they did not receive a message from person A. There are two possible explanations: (i) person A did not send the message, (ii) person B pretended not to hear the message. Given just the evidence of B's claim, there is no way to tell which of the two explanations is correct. The relation to blockchain protocol incentivization is this: if you see a protocol execution where 70% of validators' messages are included in the chain and 30% are not, and see nothing else (and this is what the blockchain sees), then there is no way to tell whether the problem is that 30% are offline or 70% are censoring. If we want to make both kinds of attacks expensive, there is only one thing that we can do: penalize both sides.Penalizing both sides allows either side to "grief" the other, by going offline if they are a minority and censoring if they are a majority. However, we can establish bounds on how easy this griefing is, through the technique of griefing factor analysis. The griefing factor of a strategy is essentially the amount of money lost by the victims divided by the amount of money lost by the attackers, and the griefing factor of a protocol is the highest griefing factor that it allows. For example, if a protocol allows me to cause you to lose $3 at a cost of $1 to myself, then the griefing factor is 3. If there are no ways to cause others to lose money, the griefing factor is zero, and if you can cause others to lose money at no cost to yourself (or at a benefit to yourself), the griefing factor is infinity.In general, wherever a speaker/listener dichotomy exists, the griefing factor cannot be globally bounded above by any value below 1. The reason is simple: either side can grief the other, so if side \(A\) can grief side \(B\) with a factor of \(x\) then side \(B\) can grief side \(A\) with a factor of \(\frac\); \(x\) and \(\frac\) cannot both be below 1 simultaneously. We can play around with the factors; for example, it may be considered okay to allow griefing factors of 2 for majority attackers in exchange for keeping the griefing factor at 0.5 for minorities, with the reasoning that minority attackers are more likely. We can also allow griefing factors of 1 for small-scale attacks, but specifically for large-scale attacks force a chain split where on one chain one side is penalized and on another chain another side is penalized, trusting the market to pick the chain where attackers are not favored. Hence there is a lot of room for compromise and making tradeoffs between different concerns within this framework.Penalizing both sides has another benefit: it ensures that if the protocol is harmed, the attacker is penalized. This ensures that whoever the attacker is, they have an incentive to avoid attacking that is commensurate with the amount of harm done to the protocol. However, if we want to bound the ratio of harm to the protocol over cost to attackers, we need a formalized way of measuring how much harm to the protocol was done.This introduces the concept of the protocol utility function - a formula that tells us how well the protocol is doing, that should ideally be calculable from inside the blockchain. In the case of a proof of work chain, this could be the percentage of all blocks produced that are in the main chain. In Casper, protocol utility is zero for a perfect execution where every epoch is finalized and no safety failures ever take place, with some penalty for every epoch that is not finalized, and a very large penalty for every safety failure. If a protocol utility function can be formalized, then penalties for faults can be set as close to the loss of protocol utility resulting from those faults as possible.

On Path Independence On Path Independence2017 Jun 22 See all posts On Path Independence Suppose that someone walks up to you and starts exclaiming to you that he thinks he has figured out how to create a source of unlimited free energy. His scheme looks as follows. First, you get a spaceship up to low Earth orbit. There, Earth's gravity is fairly high, and so the spaceship will start to accelerate heavily toward the earth. The spaceship puts itself into a trajectory so that it barely brushes past the Earth's atmosphere, and then keeps hurtling far into space. Further in space, the gravity is lower, and so the spaceship can go higher before it starts once again coming down. When it comes down, it takes a curved path toward the Earth, so as to maximize its time in low orbit, maximizing the acceleration it gets from the high gravity there, so that after it passes by the Earth it goes even higher. After it goes high enough, it flies through the Earth's atmosphere, slowing itself down but using the waste heat to power a thermal reactor. Then, it would go back to step one and keep going.Something like this: Now, if you know anything about Newtonian dynamics, chances are you'll immediately recognize that this scheme is total bollocks. But how do you know? You could make an appeal to symmetry, saying "look, for every slice of the orbital path where you say gravity gives you high acceleration, there's a corresponding slice of the orbital path where gravity gives you just as high deceleration, so I don't see where the net gains are coming from". But then, suppose the man presses you. "Ah," he says, "but in that slice where there is high acceleration your initial velocity is low, and so you spend a lot of time inside of it, whereas in the corresponding slice, your incoming velocity is high, and so you have less time to decelerate". How do you really, conclusively, prove him wrong?One approach is to dig deeply into the math, calculate the integrals, and show that the supposed net gains are in fact exactly equal to zero. But there is also a simple approach: recognize that energy is path-independent. That is, when the spaceship moves from point \(A\) to point \(B\), where point \(B\) is closer to the earth, its kinetic energy certainly goes up because its speed increases. But because total energy (kinetic plus potential) is conserved, and potential energy is only dependent on the spaceship's position, and not how it got there, we know that regardless of what path from point \(A\) to point \(B\) the spaceship takes, once it gets to point \(B\) the total change in kinetic energy will be exactly the same. Different paths, same change in energyFurthermore, we know that the kinetic energy gain from going from point \(A\) to point \(A\) is also independent of the path you take along the way: in all cases it's exactly zero.One concern sometimes cited against on-chain market makers (that is, fully automated on-chain mechanisms that act as always-available counterparties for people who wish to trade one type of token for another) is that they are invariably easy to exploit.As an example, let me quote a recent post discussing this issue in the context of Bancor:The prices that Bancor offers for tokens have nothing to do with the actual market equilibrium. Bancor will always trail the market, and in doing so, will bleed its reserves. A simple thought experiment suffices to illustrate the problem. Suppose that market panic sets around X. Unfounded news about your system overtake social media. Let's suppose that people got convinced that your CEO has absconded to a remote island with no extradition treaty, that your CFO has been embezzling money, and your CTO was buying drugs from the darknet markets and shipping them to his work address to make a Scarface-like mound of white powder on his desk. Worse, let's suppose that you know these allegations to be false. They were spread by a troll army wielded by a company with no products, whose business plan is to block everyone's coin stream. Bancor would offer ever decreasing prices for X coins during a bank run, until it has no reserves left. You'd watch the market panic take hold and eat away your reserves. Recall that people are convinced that the true value of X is 0 in this scenario, and the Bancor formula is guaranteed to offer a price above that. So your entire reserve would be gone.The post discusses many issues around the Bancor protocol, including details such as code quality, and I will not touch on any of those; instead, I will focus purely on the topic of on-chain market maker efficiency and exploitability, using Bancor (along with MKR) purely as examples and not seeing to make any judgements on the quality of either project as a whole.For many classes of naively designed on-chain market makers, the comment above about exploitability and trailing markets applies verbatim, and quite seriously so. However, there are also classes of on-chain market makers that are definitely not suspect to their entire reserve being drained due to some kind of money-pumping attack. To take a simple example, consider the market maker selling MKR for ETH whose internal state consists of a current price, \(p\), and which is willing to buy or sell an infinitesimal amount of MKR at each price level. For example, suppose that \(p = 5\), and you wanted to buy 2 MKR. The market would sell you:0.00...01 MKR at a price of 5 ETH/MKR 0.00...01 MKR at a price of 5.00...01 ETH/MKR 0.00...01 MKR at a price of 5.00...02 ETH/MKR .... 0.00...01 MKR at a price of 6.99...98 ETH/MKR 0.00...01 MKR at a price of 6.99...99 ETH/MKR Altogether, it's selling you 2 MKR at an average price of 6 ETH/MKR (ie. total cost 12 ETH), and at the end of the operation \(p\) has increased to 7. If someone then wanted to sell 1 MKR, they would be spending 6.5 ETH, and at the end of that operation \(p\) would drop back down to 6.Now, suppose that I told you that such a market maker started off at a price of \(p = 5\), and after an unspecified series of events \(p\) is now 4. Two questions:How much MKR did the market maker gain or lose? How much ETH did the market maker gain or lose? The answers are: it gained 1 MKR, and lost 4.5 ETH. Notice that this result is totally independent of the path that \(p\) took. Those answers are correct if \(p\) went from 5 to 4 directly with one buyer, they're correct if there was first one buyer that took \(p\) from 5 to 4.7 and a second buyer that took \(p\) the rest of the way to 4, and they're even correct if \(p\) first dropped to 2, then increased to 9.818, then dropped again to 0.53, then finally rose again to 4.Why is this the case? The simplest way to see this is to see that if \(p\) drops below 4 and then comes back up to 4, the sells on the way down are exactly counterbalanced by buys on the way up; each sell has a corresponding buy of the same magnitude at the exact same price. But we can also see this by viewing the market maker's core mechanism differently. Define the market maker as having a single-dimensional internal state \(p\), and having MKR and ETH balances defined by the following formulas:\(mkr\_balance(p) = 10 - p\)\(eth\_balance(p) = p^2/2\)Anyone has the power to "edit" \(p\) (though only to values between 0 and 10), but they can only do so by supplying the right amount of MKR or ETH, and getting the right amount of MKR and ETH back, so that the balances still match up; that is, so that the amount of MKR and ETH held by the market maker after the operation is the amount that they are supposed to hold according to the above formulas, with the new value for \(p\) that was set. Any edit to \(p\) that does not come with MKR and ETH transactions that make the balances match up automatically fails.Now, the fact that any series of events that drops \(p\) from 5 to 4 also raises the market maker's MKR balance by 1 and drops its ETH balance by 4.5, regardless of what series of events it was, should look elementary: \(mkr\_balance(4) - mkr\_balance(5) = 1\) and \(eth\_balance(4) - eth\_balance(5) = -4.5\).What this means is that a "reserve bleeding" attack on a market maker that preserves this kind of path independence property is impossible. Even if some trolls successfully create a market panic that drops prices to near-zero, when the panic subsides, and prices return to their original levels, the market maker's position will be unchanged - even if both the price, and the market maker's balances, made a bunch of crazy moves in the meantime.Now, this does not mean that market makers cannot lose money, compared to other holding strategies. If, when you start off, 1 MKR = 5 ETH, and then the MKR price moves, and we compare the performance of holding 5 MKR and 12.5 ETH in the market maker versus the performance of just holding the assets, the result looks like this: Holding a balanced portfolio always wins, except in the case where prices stay exactly the same, in which case the returns of the market maker and the balanced portfolio are equal. Hence, the purpose of a market maker of this type is to subsidize guaranteed liquidity as a public good for users, serving as trader of last resort, and not to earn revenue. However, we certainly can modify the market maker to earn revenue, and quite simply: we have it charge a spread. That is, the market maker might charge \(1.005\cdot p\) for buys and offer only \(0.995\cdot p\) for sells. Now, being the beneficiary of a market maker becomes a bet: if, in the long run, prices tend to move in one direction, then the market maker loses, at least relative to what they could have gained if they had a balanced portfolio. If, on the other hand, prices tend to bounce around wildly but ultimately come back to the same point, then the market maker can earn a nice profit. This sacrifices the "path independence" property, but in such a way that any deviations from path independence are always in the market maker's favor.There are many designs that path-independent market makers could take; if you are willing to create a token that can issue an unlimited quantity of units, then the "constant reserve ratio" mechanism (where for some constant ratio \(0 \leq r \leq 1\), the token supply is \(p^\) and the reserve size is \(r \cdot p^\) also counts as one, provided that it is implemented correctly and path independence is not compromised by bounds and rounding errors.If you want to make a market maker for existing tokens without a price cap, my favorite (credit to Martin Koppelmann) mechanism is that which maintains the invariant \(tokenA\_balance(p) \cdot tokenB\_balance(p) = k\) for some constant \(k\). So the formulas would be:\(tokenA\_balance(p) = \sqrt\)\(tokenB\_balance(p) = \sqrt\) Where \(p\) is the price of \(tokenB\) denominated in \(tokenA\). In general, you can make a path-independent market maker by defining any (monotonic) relation between \(tokenA\_balance\) and \(tokenB\_balance\) and calculating its derivative at any point to give the price.The above only discusses the role of path independence in preventing one particular type of issue: that where an attacker somehow makes a series of transactions in the context of a series of price movements in order to repeatedly drain the market maker of money. With a path independent market maker, such "money pump" vulnerabilities are impossible. However, there certainly are other kinds of inefficiencies that may exist. If the price of MKR drops from 5 ETH to 1 ETH, then the market maker used in the example above will have lost 28 ETH worth of value, whereas a balanced portfolio would only have lost 20 ETH. Where did that 8 ETH go?In the best case, the price (that is to say, the "real" price, the price level where supply and demand among all users and traders matches up) drops quickly, and some lucky trader snaps up the deal, claiming an 8 ETH profit minus negligible transaction fees. But what if there are multiple traders? Then, if the price between block \(n\) and block \(n+1\) differs, the fact that traders can bid against each other by setting transaction fees creates an all-pay auction, with revenues going to the miner. As a consequence of the revenue equivalence theorem, we can deduce that we can expect that the transaction fees that traders send into this mechanism will keep going up until they are roughly equal to the size of the profit earned (at least initially; the real equilibrium is for miners to just snap up the money themselves). Hence, either way schemes like this are ultimately a gift to the miners.One way to increase social welfare in such a design is to make it possible to create purchase transactions that are only worthwhile for miners to include if they actually make the purchase. That is, if the "real" price of MKR falls from 5 to 4.9, and there are 50 traders racing to arbitrage the market maker, and only the first one of those 50 will make the trade, then only that one should pay the miner a transaction fee. This way, the other 49 failed trades will not clog up the blockchain. EIP 86, slated for Metropolis, opens up a path toward standardizing such a conditional transaction fee mechanism (another good side effect is that this can also make token sales more unobtrusive, as similar all-pay-auction mechanics apply in many token sales).Additionally, there are other inefficiencies if the market maker is the only available trading venue for tokens. For example, if two traders want to exchange a large amount, then they would need to do so via a long series of small buy and sell transactions, needlessly clogging up the blockchain. To mitigate such efficiencies, an on-chain market maker should only be one of the trading venues available, and not the only one. However, this is arguably not a large concern for protocol developers; if there ends up being a demand for a venue for facilitating large-scale trades, then someone else will likely provide it.Furthermore, the arguments here only talk about path independence of the market maker assuming a given starting price and ending price. However, because of various psychological effects, as well as multi-equilibrium effects, the ending price is plausibly a function not just of the starting price and recent events that affect the "fundamental" value of the asset, but also of the pattern of trades that happens in response to those events. If a price-dropping event takes place, and because of poor liquidity the price of the asset drops quickly, it may end up recovering to a lower point than if more liquidity had been present in the first place. That said, this may actually be an argument in favor of subsidied market makers: if such multiplier effects exist, then they will have a positive impact on price stability that goes beyond the first-order effect of the liquidity that the market maker itself provides.There is likely a lot of research to be done in determining exactly which path-independent market maker is optimal. There is also the possibility of hybrid semi-automated market makers that have the same guaranteed-liquidity properties, but which include some element of asynchrony, as well as the ability for the operator to "cut in line" and collect the profits in cases where large amounts of capital would otherwise be lost to miners. There is also not yet a coherent theory of just how much (if any) on-chain automated guaranteed liquidity is optimal for various objectives, and to what extent, and by whom, these market makers should be subsidized. All in all, the on-chain mechanism design space is still in its early days, and it's certainly worth much more broadly researching and exploring various options.

Analyzing Token Sale Models Analyzing Token Sale Models2017 Jun 09 See all posts Analyzing Token Sale Models Note: I mention the names of various projects below only to compare and contrast their token sale mechanisms; this should NOT be taken as an endorsement or criticism of any specific project as a whole. It's entirely possible for any given project to be total trash as a whole and yet still have an awesome token sale model.The last few months have seen an increasing amount of innovation in token sale models. Two years ago, the space was simple: there were capped sales, which sold a fixed number of tokens at a fixed price and hence fixed valuation and would often quickly sell out, and there were uncapped sales, which sold as many tokens as people were willing to buy. Now, we have been seeing a surge of interest, both in terms of theoretical investigation and in many cases real-world implementation, of hybrid capped sales, reverse dutch auctions, Vickrey auctions, proportional refunds, and many other mechanisms.Many of these mechanisms have arisen as responses to perceived failures in previous designs. Nearly every significant sale, including Brave's Basic Attention Tokens, Gnosis, upcoming sales such as Bancor, and older ones such as Maidsafe and even the Ethereum sale itself, has been met with a substantial amount of criticism, all of which points to a simple fact: so far, we have still not yet discovered a mechanism that has all, or even most, of the properties that we would like.Let us review a few examples.Maidsafe The decentralized internet platform raised $7m in five hours. However, they made the mistake of accepting payment in two currencies (BTC and MSC), and giving a favorable rate to MSC buyers. This led to a temporary ~2x appreciation in the MSC price, as users rushed in to buy MSC to participate in the sale at the more favorable rate, but then the price saw a similarly steep drop after the sale ended. Many users converted their BTC to MSC to participate in the sale, but then the sale closed too quickly for them, leading to them being stuck with a ~30% loss.This sale, and several others after it (cough cough WeTrust, TokenCard), showed a lesson that should hopefully by now be uncontroversial: running a sale that accepts multiple currencies at a fixed exchange rate is dangerous and bad. Don't do it.EthereumThe Ethereum sale was uncapped, and ran for 42 days. The sale price was 2000 ETH for 1 BTC for the first 14 days, and then started increasing linearly, finishing at 1337 ETH for 1 BTC. Nearly every uncapped sale is criticized for being "greedy" (a criticism I have significant reservations about, but we'll get back to this later), though there is also another more interesting criticism of these sales: they give participants high uncertainty about the valuation that they are buying at. To use a not-yet-started sale as a example, there are likely many people who would be willing to pay $10,000 for a pile of Bancor tokens if they knew for a fact that this pile represented 1% of all Bancor tokens in existence, but many of them would become quite apprehensive if they were buying a pile of, say, 5000 Bancor tokens, and they had no idea whether the total supply would be 50000, 500000 or 500 million.In the Ethereum sale, buyers who really cared about predictability of valuation generally bought on the 14th day, reasoning that this was the last day of the full discount period and so on this day they had maximum predictability together with the full discount, but the pattern above is hardly economically optimal behavior; the equilibrium would be something like everyone buying in on the last hour of the 14th day, making a private tradeoff between certainty of valuation and taking the 1.5% hit (or, if certainty was really important, purchases could spill over into the 15th, 16th and later days). Hence, the model certainly has some rather weird economic properties that we would really like to avoid if there is a convenient way to do so.BATThroughout 2016 and early 2017, the capped sale design was most popular. Capped sales have the property that it is very likely that interest is oversubscribed, and so there is a large incentive to getting in first. Initially, sales took a few hours to finish. However, soon the speed began to accelerate. First Blood made a lot of news by finishing their $5.5m sale in two minutes - while active denial-of-service attacks on the Ethereum blockchain were taking place. However, the apotheosis of this race-to-the-Nash-equilibrium did not come until the BAT sale last month, when a $35m sale was completed within 30 seconds due to the large amount of interest in the project. Not only did the sale finish within two blocks, but also:The total transaction fees paid were 70.15 ETH (>$15,000), with the highest single fee being ~$6,600 185 purchases were successful, and over 10,000 failed The Ethereum blockchain's capacity was full for 3 hours after the sale started Thus, we are starting to see capped sales approach their natural equilibrium: people trying to outbid each other's transaction fees, to the point where potentially millions of dollars of surplus would be burned into the hands of miners. And that's before the next stage starts: large mining pools butting into the start of the line and just buying up all of the tokens themselves before anyone else can.GnosisThe Gnosis sale attempted to alleviate these issues with a novel mechanism: the reverse dutch auction. The terms, in simplified form, are as follows. There was a capped sale, with a cap of $12.5 million USD. However, the portion of tokens that would actually be given to purchasers depended on how long the sale took to finish. If it finished on the first day, then only ~5% of tokens would be distributed among purchasers, and the rest held by the Gnosis team; if it finished on the second day, it would be ~10%, and so forth.The purpose of this is to create a scheme where, if you buy at time \(T\), then you are guaranteed to buy in at a valuation which is at most \(\frac\). The goal is to create a mechanism where the optimal strategy is simple. First, you personally decide what is the highest valuation you would be willing to buy at (call it V). Then, when the sale starts, you don't buy in immediately; rather, you wait until the valuation drops to below that level, and then send your transaction.There are two possible outcomes:The sale closes before the valuation drops to below V. Then, you are happy because you stayed out of what you thought is a bad deal. The sale closes after the valuation drops to below V. Then, you sent your transaction, and you are happy because you got into what you thought is a good deal. However, many people predicted that because of "fear of missing out" (FOMO), many people would just "irrationally" buy in at the first day, without even looking at the valuation. And this is exactly what happened: the sale finished in a few hours, with the result that the sale reached its cap of $12.5 million when it was only selling about 5% of all tokens that would be in existence - an implied valuation of over $300 million.All of this would of course be an excellent piece of confirming evidence for the narrative that markets are totally irrational, people don't think clearly before throwing in large quantities of money (and often, as a subtext, that the entire space needs to be somehow suppressed to prevent further exuberance) if it weren't for one inconvenient fact: the traders who bought into the sale were right. Even in ETH terms, despite the massive ETH price rise, the price of 1 GNO has increased from ~0.6 ETH to ~0.8 ETH.What happened? A couple of weeks before the sale started, facing public criticism that if they end up holding the majority of the coins they would act like a central bank with the ability to heavily manipulate GNO prices, the Gnosis team agreed to hold 90% of the coins that were not sold for a year. From a trader's point of view, coins that are locked up for a long time are coins that cannot affect the market, and so in a short term analysis, might as well not exist. This is what initially propped up Steem to such a high valuation last year in July, as well as Zcash in the very early moments when the price of each coin was over $1,000.Now, one year is not that long a time, and locking up coins for a year is nowhere close to the same thing as locking them up forever. However, the reasoning goes further. Even after the one year holding period expires, you can argue that it is in the Gnosis team's interest to only release the locked coins if they believe that doing so will make the price go up, and so if you trust the Gnosis team's judgement this means that they are going to do something which is at least as good for the GNO price as simply locking up the coins forever. Hence, in reality, the GNO sale was really much more like a capped sale with a cap of $12.5 million and a valuation of $37.5 million. And the traders who participated in the sale reacted exactly as they should have, leaving scores of internet commentators wondering what just happened.There is certainly a weird bubbliness about crypto-assets, with various no-name assets attaining market caps of $1-100 million (including BitBean as of the time of this writing at $12m, PotCoin at $22m, PepeCash at $13m and SmileyCoin at $14.7m) just because. However, there's a strong case to be made that the participants at the sale stage are in many cases doing nothing wrong, at least for themselves; rather, traders who buy in sales are simply (correctly) predicting the existence of an ongoing bubble has been brewing since the start of 2015 (and arguably, since the start of 2010).More importantly though, bubble behavior aside, there is another legitimate criticism of the Gnosis sale: despite their 1-year no-selling promise, eventually they will have access to the entirety of their coins, and they will to a limited extent be able to act like a central bank with the ability to heavily manipulate GNO prices, and traders will have to deal with all of the monetary policy uncertainty that that entails.Specifying the problemSo what would a good token sale mechanism look like? One way that we can start off is by looking through the criticisms of existing sale models that we have seen and coming up with a list of desired properties.Let's do that. Some natural properties include:Certainty of valuation - if you participate in a sale, you should have certainty over at least a ceiling on the valuation (or, in other words, a floor on the percentage of all tokens you are getting). Certainty of participation - if you try to participate in a sale, you should be able to generally count on succeeding. Capping the amount raised - to avoid being perceived as greedy (or possibly to mitigate risk of regulatory attention), the sale should have a limit on the amount of money it is collecting. No central banking - the token sale issuer should not be able to end up with an unexpectedly very large percentage of the tokens that would give them control over the market. Efficiency - the sale should not lead to substantial economic inefficiencies or deadweight losses. Sounds reasonable?Well, here's the not-so-fun part.(1) and (2) cannot be fully satisfied simultaneously. At least without resorting to very clever tricks, (3), (4) and (5) cannot be satisfied simultaneously. These can be cited as "the first token sale dilemma" and "the second token sale trilemma".The proof for the first dilemma is easy: suppose you have a sale where you provide users with certainty of a $100 million valuation. Now, suppose that users try to throw $101 million into the sale. At least some will fail. The proof for the second trilemma is a simple supply-and-demand argument. If you satisfy (4), then you are selling all, or some fixed large percentage, of the tokens, and so the valuation you are selling at is proportional to the price you are selling at. If you satisfy (3), then you are putting a cap on the price. However, this implies the possibility that the equilibrium price at the quantity you are selling exceeds the price cap that you set, and so you get a shortage, which inevitably leads to either (i) the digital equivalent of standing in line for 4 hours at a very popular restaurant, or (ii) the digital equivalent of ticket scalping - both large deadwight losses, contradicting (5).The first dilemma cannot be overcome; some valuation uncertainty or participation uncertainty is inescapable, though when the choice exists it seems better to try to choose participation uncertainty rather than valuation uncertainty. The closest that we can come is compromising on full participation to guarantee partial participation. This can be done with a proportional refund (eg. if $101 million buy in at a $100 million valuation, then everyone gets a 1% refund). We can also think of this mechanism as being an uncapped sale where part of the payment comes in the form of locking up capital rather than spending it; from this viewpoint, however, it becomes clear that the requirement to lock up capital is an efficiency loss, and so such a mechanism fails to satisfy (5). If ether holdings are not well-distributed then it arguably harms fairness by favoring wealthy stakeholders.The second dilemma is difficult to overcome, and many attempts to overcome it can easily fail or backfire. For example, the Bancor sale is considering limiting the transaction gas price for purchases to 50 shannon (~12x the normal gasprice). However, this now means that the optimal strategy for a buyer is to set up a large number of accounts, and from each of those accounts send a transaction that triggers a contract, which then attempts to buy in (the indirection is there to make it impossible for the buyer to accidentally buy in more than they wanted, and to reduce capital requirements). The more accounts a buyer sets up, the more likely they are to get in. Hence, in equilibrium, this could lead to even more clogging of the Ethereum blockchain than a BAT-style sale, where at least the $6600 fees were spent on a single transaction and not an entire denial-of-service attack on the network. Furthermore, any kind of on-chain transaction spam contest severely harms fairness, because the cost of participating in the contest is constant, whereas the reward is proportional to how much money you have, and so the result disproportionately favors wealthy stakeholders.Moving forwardThere are three more clever things that you can do. First, you can do a reverse dutch auction just like Gnosis, but with one change: instead of holding the unsold tokens, put them toward some kind of public good. Simple examples include: (i) airdrop (ie. redistributing to all ETH holders), (ii) donating to the Ethereum Foundation, (iii) donating to Parity, Brainbot, Smartpool or other companies and individuals independently building infrastructure for the Ethereum space, or (iv) some combination of all three, possibly with the ratios somehow being voted on by the token buyers.Second, you can keep the unsold tokens, but solve the "central banking" problem by committing to a fully automated plan for how they would be spent. The reasoning here is similar to that for why many economists are interested in rules-based monetary policy: even if a centralized entity has a large amount of control over a powerful resource, much of the political uncertainty that results can be mitigated if the entity credibly commits to following a set of programmatic rules for how they apply it. For example, the unsold tokens can be put into a market maker that is tasked with preserving the tokens' price stability.Third, you can do a capped sale, where you limit the amount that can be bought by each person. Doing this effectively requires a KYC process, but the nice thing is a KYC entity can do this once, whitelisting users' addresses after they verify that the address represents a unique individual, and this can then be reused for every token sale, alongside other applications that can benefit from per-person sybil resistance like Akasha's quadratic voting. There is still deadweight loss (ie. inefficiency) here, because this will lead to individuals with no personal interest in tokens participating in sales because they know they will be able to quickly flip them on the market for a profit. However, this is arguably not that bad: it creates a kind of crypto universal basic income, and if behavioral economics assumptions like the endowment effect are even slightly true it will also succeed at the goal of ensuring widely distributed ownership.Are single round sales even good?Let us get back to the topic of "greed". I would claim that not many people are, in principle, opposed to the idea of development teams that are capable of spending $500 million to create a really great project getting $500 million. Rather, what people are opposed to is (i) the idea of completely new and untested development teams getting $50 million all at once, and (ii) even more importantly, the time mismatch between developers' rewards and token buyers' interests. In a single-round sale, the developers have only one chance to get money to build the project, and that is near the start of the development process. There is no feedback mechanism where teams are first given a small amount of money to prove themselves, and then given access to more and more capital over time as they prove themselves to be reliable and successful. During the sale, there is comparatively little information to filter between good development teams and bad ones, and once the sale is completed, the incentive to developers to keep working is relatively low compared to traditional companies. The "greed" isn't about getting lots of money, it's about getting lots of money without working hard to show you're capable of spending it wisely.If we want to strike at the heart of this problem, how would we solve it? I would say the answer is simple: start moving to mechanisms other than single round sales.I can offer several examples as inspiration:Angelshares - this project ran a sale in 2014 where it sold off a fixed percentage of all AGS every day for a period of several months. During each day, people could contribute an unlimited amount to the crowdsale, and the AGS allocation for that day would be split among all contributors. Basically, this is like having a hundred "micro-rounds" of uncapped sales over the course of most of a year; I would claim that the duration of the sales could be stretched even further. Mysterium, which held a little-noticed micro-sale six months before the big one. Bancor, which recently agreed to put all funds raised over a cap into a market maker which will maintain price stability along with maintaining a price floor of 0.01 ETH. These funds cannot be removed from the market maker for two years. It seems hard to see the relationship between Bancor's strategy and solving time mismatch incentives, but an element of a solution is there. To see why, consider two scenarios. As a first case, suppose the sale raises $30 million, the cap is $10 million, but then after one year everyone agrees that the project is a flop. In this case, the price would try to drop below 0.01 ETH, and the market maker would lose all of its money trying to maintain the price floor, and so the team would only have $10 million to work with. As a second case, suppose the sale raises $30 million, the cap is $10 million, and after two years everyone is happy with the project. In this case, the market maker will not have been triggered, and the team would have access to the entire $30 million.A related proposal is Vlad Zamfir's "safe token sale mechanism". The concept is a very broad one that could be parametrized in many ways, but one way to parametrize it is to sell coins at a price ceiling and then have a price floor slightly below that ceiling, and then allow the two to diverge over time, freeing up capital for development over time if the price maintains itself.Arguably, none of the above three are sufficient; we want sales that are spread out over an even longer period of time, giving us much more time to see which development teams are the most worthwhile before giving them the bulk of their capital. But nevertheless, this seems like the most productive direction to explore in.Coming out of the DilemmasFrom the above, it should hopefully be clear that while there is no way to counteract the dilemma and trilemma head on, there are ways to chip away at the edges by thinking outside the box and compromising on variables that are not apparent from a simplistic view of the problem. We can compromise on guarantee of participation slightly, mitigating the impact by using time as a third dimension: if you don't get in during round \(N\), you can just wait until round \(N+1\) which will be in a week and where the price probably will not be that different.We can have a sale which is uncapped as a whole, but which consists of a variable number of periods, where the sale within each period is capped; this way teams would not be asking for very large amounts of money without proving their ability to handle smaller rounds first. We can sell small portions of the token supply at a time, removing the political uncertainty that this entails by putting the remaining supply into a contract that continues to sell it automatically according to a prespecified formula.Here are a few possible mechanisms that follow some of the spirit of the above ideas:Host a Gnosis-style reverse dutch auction with a low cap (say, $1 million). If the auction sells less than 100% of the token supply, automatically put the remaining funds into another auction two months later with a 30% higher cap. Repeat until the entire token supply is sold. Sell an unlimited number of tokens at a price of \(\$X\) and put 90% of the proceeds into a smart contract that guarantees a price floor of \(\$0.9 \cdot X\). Have the price ceiling go up hyperbolically toward infinity, and the price floor go down linearly toward zero, over a five-year period. Do the exact same thing AngelShares did, though stretch it out over 5 years instead of a few months. Host a Gnosis-style reverse dutch auction. If the auction sells less than 100% of the token supply, put the remaining funds into an automated market maker that attempts to ensure the token's price stability (note that if the price continues going up anyway, then the market maker would be selling tokens, and some of these earnings could be given to the development team). Immediately put all tokens into a market maker with parameters+variables \(X\) (minimum price), \(s\) (fraction of all tokens already sold), \(t\) (time since sale started), \(T\) (intended duration of sale, say 5 years), that sells tokens at a price of \(\dfrac)}\) (this one is weird and may need to be economically studied more). Note that there are other mechanisms that should be tried to solve other problems with token sales; for example, revenues going into a multisig of curators, which only hand out funds if milestones are being met, is one very interesting idea that should be done more. However, the design space is highly multidimensional, and there are a lot more things that could be tried.

Engineering Security Through Coordination Problems Engineering Security Through Coordination Problems2017 May 08 See all posts Engineering Security Through Coordination Problems Recently, there was a small spat between the Core and Unlimited factions of the Bitcoin community, a spat which represents perhaps the fiftieth time the same theme was debated, but which is nonetheless interesting because of how it highlights a very subtle philosophical point about how blockchains work.ViaBTC, a mining pool that favors Unlimited, tweeted "hashpower is law", a usual talking point for the Unlimited side, which believes that miners have, and should have, a very large role in the governance of Bitcoin, the usual argument for this being that miners are the one category of users that has a large and illiquid financial incentive in Bitcoin's success. Greg Maxwell (from the Core side) replied that "Bitcoin's security works precisely because hash power is NOT law".The Core argument is that miners only have a limited role in the Bitcoin system, to secure the ordering of transactions, and they should NOT have the power to determine anything else, including block size limits and other block validity rules. These constraints are enforced by full nodes run by users - if miners start producing blocks according to a set of rules different than the rules that users' nodes enforce, then the users' nodes will simply reject the blocks, regardless of whether 10% or 60% or 99% of the hashpower is behind them. To this, Unlimited often replies with something like "if 90% of the hashpower is behind a new chain that increases the block limit, and the old chain with 10% hashpower is now ten times slower for five months until difficulty readjusts, would youreallynot update your client to accept the new chain?"Many people often argue against the use of public blockchains for applications that involve real-world assets or anything with counterparty risk. The critiques are either total, saying that there is no point in implementing such use cases on public blockchains, or partial, saying that while there may be advantages to storing the data on a public chain, the business logic should be executed off chain.The argument usually used is that in such applications, points of trust exist already - there is someone who owns the physical assets that back the on-chain permissioned assets, and that someone could always choose to run away with the assets or be compelled to freeze them by a government or bank, and so managing the digital representations of these assets on a blockchain is like paying for a reinforced steel door for one's house when the window is open. Instead, such systems should use private chains, or even traditional server-based solutions, perhaps adding bits and pieces of cryptography to improve auditability, and thereby save on the inefficiencies and costs of putting everything on a blockchain.The arguments above are both flawed in their pure forms, and they are flawed in a similar way. While it is theoretically possible for miners to switch 99% of their hashpower to a chain with new rules (to make an example where this is uncontroversially bad, suppose that they are increasing the block reward), and even spawn-camp the old chain to make it permanently useless, and it is also theoretically possible for a centralized manager of an asset-backed currency to cease honoring one digital token, make a new digital token with the same balances as the old token except with one particular account's balance reduced to zero, and start honoring the new token, in practice those things are both quite hard to do.In the first case, users will have to realize that something is wrong with the existing chain, agree that they should go to the new chain that the miners are now mining on, and download the software that accepts the new rules. In the second case, all clients and applications that depend on the original digital token will break, users will need to update their clients to switch to the new digital token, and smart contracts with no capacity to look to the outside world and see that they need to update will break entirely. In the middle of all this, opponents of the switch can create a fear-uncertainty-and-doubt campaign to try to convince people that maybe they shouldn't update their clients after all, or update their client to some third set of rules (eg. changing proof of work), and this makes implementing the switch even more difficult.Hence, we can say that in both cases, even though there theoretically are centralized or quasi-centralized parties that could force a transition from state A to state B, where state B is disagreeable to users but preferable to the centralized parties, doing so requires breaking through a hard coordination problem. Coordination problems are everywhere in society and are often a bad thing - while it would be better for most people if the English language got rid of its highly complex and irregular spelling system and made a phonetic one, or if the United States switched to metric, or if we could immediately drop all prices and wages by ten percent in the event of a recession, in practice this requires everyone to agree on the switch at the same time, and this is often very very hard.With blockchain applications, however, we are doing something different: we are using coordination problems to our advantage, using the friction that coordination problems create as a bulwark against malfeasance by centralized actors. We can build systems that have property X, and we can guarantee that they will preserve property X to a high degree because changing the rules from X to not-X would require a whole bunch of people to agree to update their software at the same time. Even if there is an actor that could force the change, doing so would be hard. This is the kind of security that you gain from client-side validation of blockchain consensus rules.Note that this kind of security relies on the decentralization of users specifically. Even if there is only one miner in the world, there is still a difference between a cryptocurrency mined by that miner and a PayPal-like centralized system. In the latter case, the operator can choose to arbitrarily change the rules, freeze people's money, offer bad service, jack up their fees or do a whole host of other things, and the coordination problems are in the operator's favor, as such systems have substantial network effects and so very many users would have to agree at the same time to switch to a better system. In the former case, client-side validation means that many attempts at mischief that the miner might want to engage in are by default rejected, and the coordination problem now works in the users' favor.Note that the arguments above do NOT, by themselves, imply that it is a bad idea for miners to be the principal actors coordinating and deciding the block size (or in Ethereum's case, the gas limit). It may well be the case that, in the specific case of the block size/gas limit, "government by coordinated miners with aligned incentives" is the optimal approach for deciding this one particular policy parameter, perhaps because the risk of miners abusing their power is lower than the risk that any specific chosen hard limit will prove wildly inappropriate for market conditions a decade after the limit is set. However, there is nothing unreasonable about saying that government-by-miners is the best way to decide one policy parameter, and at the same saying that for other parameters (eg. block reward) we want to rely on client-side validation to ensure that miners are constrained. This is the essence of engineering decentralized instutitions: it is about strategically using coordination problems to ensure that systems continue to satisfy certain desired properties.The arguments above also do not imply that it is always optimal to try to put everything onto a blockchain even for services that are trust-requiring. There generally are at least some gains to be made by running more business logic on a blockchain, but they are often much smaller than the losses to efficiency or privacy. And this ok; the blockchain is not the best tool for every task. What the arguments abovedoimply, though, is that if you are building a blockchain-based application that contains many centralized components out of necessity, then you can make substantial further gains in trust-minimization by giving users a way to access your application through a regular blockchain client (eg. in the case of Ethereum, this might be Mist, Parity, Metamask or Status), instead of getting them to use a web interface that you personally control.Theoretically, the benefits of user-side validation are optimized if literally every user runs an independent "ideal full node" - a node that accepts all blocks that follow the protocol rules that everyone agreed to when creating the system, and rejects all blocks that do not. In practice, however, this involves asking every user to process every transaction run by everyone in the network, which is clearly untenable, especially keeping in mind the rapid growth of smartphone users in the developing world.There are two ways out here. The first is that we can realize that while it is optimal from the point of view of the above arguments that everyone runs a full node, it is certainly not required. Arguably, any major blockchain running at full capacity will have already reached the point where it will not make sense for "the common people" to expend a fifth of their hard drive space to run a full node, and so the remaining users are hobbyists and businesses. As long as there is a fairly large number of them, and they come from diverse backgrounds, the coordination problem of getting these users to collude will still be very hard.Second, we can rely on strong light client technology.There are two levels of "light clients" that are generally possible in blockchain systems. The first, weaker, kind of light client simply convinces the user, with some degree of economic assurance, that they are on the chain that is supported by the majority of the network. This can be done much more cheaply than verifying the entire chain, as all clients need to do is in proof of work schemes verify nonces or in proof stake schemes verify signed certificates that state "either the root hash of the state is what I say it is, or you can publish this certificate into the main chain to delete a large amount of my money". Once the light client verifies a root hash, they can use Merkle trees to verify any specific piece of data that they might want to verify. Look, it's a Merkle tree! The second level is a "nearly fully verifying" light client. This kind of client doesn't just try to follow the chain that the majority follows; rather, it also tries to follow only chains that follow all the rules. This is done by a combination of strategies; the simplest to explain is that a light client can work together with specialized nodes (credit to Gavin Wood for coming up with the name "fishermen") whose purpose is to look for blocks that are invalid and generate "fraud proofs", short messages that essentially say "Look! This block has a flaw over here!". Light clients can then verify that specific part of a block and check if it's actually invalid.If a block is found to be invalid, it is discarded; if a light client does not hear any fraud proofs for a given block for a few minutes, then it assumes that the block is probably legitimate. There's a bit more complexity involved in handling the case where the problem is not data that is bad, but rather data that is missing, but in general it is possible to get quite close to catching all possible ways that miners or validators can violate the rules of the protocol.Note that in order for a light client to be able to efficiently validate a set of application rules, those rules must be executed inside of consensus - that is, they must be either part of the protocol or part of a mechanism executing inside the protocol (like a smart contract). This is a key argument in favor of using the blockchain for both data storage and business logic execution, as opposed to just data storage.These light client techniques are imperfect, in that they do rely on assumptions about network connectivity and the number of other light clients and fishermen that are in the network. But it is actually not crucial for them to work 100% of the time for 100% of validators. Rather, all that we want is to create a situation where any attempt by a hostile cartel of miners/validators to push invalid blocks without user consent will cause a large amount of headaches for lots of people and ultimately require everyone to update their software if they want to continue to synchronize with the invalid chain. As long as this is satisfied, we have achieved the goal of security through coordination frictions.

Hard Forks, Soft Forks, Defaults and Coercion Hard Forks, Soft Forks, Defaults and Coercion2017 Mar 14 See all posts Hard Forks, Soft Forks, Defaults and Coercion One of the important arguments in the blockchain space is that of whether hard forks or soft forks are the preferred protocol upgrade mechanism. The basic difference between the two is that soft forks change the rules of a protocol by strictly reducing the set of transactions that is valid, so nodes following the old rules will still get on the new chain (provided that the majority of miners/validators implements the fork), whereas hard forks allow previously invalid transactions and blocks to become valid, so clients must upgrade their clients in order to stay on the hard-forked chain. There are also two sub-types of hard forks: strictly expanding hard forks, which strictly expand the set of transactions that is valid, and so effectively the old rules are a soft fork with respect to the new rules, and bilateral hard forks, where the two rulesets are incompatible both ways.Here is a Venn diagram to illustrate the fork types: The benefits commonly cited for the two are as follows.Hard forks allow the developers much more flexibility in making the protocol upgrade, as they do not have to take care to make sure that the new rules "fit into" the old rules Soft forks are more convenient for users, as users do not need to upgrade to stay on the chain Soft forks are less likely to lead to a chain split Soft forks only really require consent from miners/validators (as even if users still use the old rules, if the nodes making the chain use the new rules then only things valid under the new rules will get into the chain in any case); hard forks require opt-in consent from users Aside from this, one major criticism often given for hard forks is that hard forks are "coercive". The kind of coercion implied here is not physical force; rather, it's coercion through network effect. That is, if the network changes rules from A to B, then even if you personally like A, if most other users like B and switch to B then you have to switch to B despite your personal disapproval of the change in order to be on the same network as everyone else.Proponents of hard forks are often derided as trying to effect a "hostile take over" of a network, and "force" users to go along with them. Additionally, the risk of chain splits is often used to bill hard forks as "unsafe".It is my personal viewpoint that these criticisms are wrong, and furthermore in many cases completely backwards. This viewpoint is not specific to Ethereum, or Bitcoin, or any other blockchain; it arises out of general properties of these systems, and is applicable to any of them. Furthermore, the arguments below only apply to controversial changes, where a large portion of at least one constituency (miners/validators and users) disapprove of them; if a change is non-contentious, then it can generally be done safely no matter what the format of the fork is.First of all, let us discuss the question of coercion. Hard forks and soft forks both change the protocol in ways that some users may not like; any protocol change will do this if it has less than exactly 100% support. Furthermore, it is almost inevitable that at least some of the dissenters, in any scenario, value the network effect of sticking with the larger group more than they value their own preferences regarding the protocol rules. Hence, both fork types are coercive, in the network-effect sense of the word.However, there is an essential difference between hard forks and soft forks: hard forks are opt-in, whereas soft forks allow users no "opting" at all. In order for a user to join a hard forked chain, they must personally install the software package that implements the fork rules, and the set of users that disagrees with a rule change even more strongly than they value network effects can theoretically simply stay on the old chain - and, practically speaking, such an event has already happened.This is true in the case of both strictly expanding hard forks and bilateral hard forks. In the case of soft forks, however, if the fork succeeds the unforked chain does not exist. Hence, soft forks clearly institutionally favor coercion over secession, whereas hard forks have the opposite bias. My own moral views lead me to favor secession over coercion, though others may differ (the most common argument raised is that network effects are really really important and it is essential that "one coin rule them all", though more moderate versions of this also exist).If I had to guess why, despite these arguments, soft forks are often billed as "less coercive" than hard forks, I would say that it is because it feels like a hard fork "forces" the user into installing a software update, whereas with a soft fork users do not "have" to do anything at all. However, this intuition is misguided: what matters is not whether or not individual users have to perform the simple bureaucratic step of clicking a "download" button, but rather whether or not the user is coerced into accepting a change in protocol rules that they would rather not accept. And by this metric, as mentioned above, both kinds of forks are ultimately coercive, and it is hard forks that come out as being somewhat better at preserving user freedom.Now, let's look at highly controversial forks, particularly forks where miner/validator preferences and user preferences conflict. There are three cases here: (i) bilateral hard forks, (ii) strictly expanding hard forks, and (iii) so-called "user-activated soft forks" (UASF). A fourth category is where miners activate a soft fork without user consent; we will get to this later.First, bilateral hard forks. In the best case, the situation is simple. The two coins trade on the market, and traders decide the relative value of the two. From the ETC/ETH case, we have overwhelming evidence that miners are overwhelmingly likely to simply assign their hashrate to coins based on the ratio of prices in order to maximize their profit, regardless of their own ideological views. Even if some miners profess ideological preferences toward one side or the other, it is overwhemingly likely that there will be enough miners that are willing to arbitrage any mismatch between price ratio and hashpower ratio, and bring the two into alignment. If a cartel of miners tries to form to not mine on one chain, there are overwheming incentives to defect.There are two edge cases here. The first is the possibilty that, because of an inefficient difficulty adjustment algorithm, the value of mining the coin goes down becase price drops but difficulty does not go down to compensate, making mining very unprofitable, and there are no miners willing to mine at a loss to keep pushing the chain forward until its difficulty comes back into balance. This was not the case with Ethereum, but may well be the case with Bitcoin. Hence, the minority chain may well simply never get off the ground, and so it will die. Note that the normative question of whether or not this is a good thing depends on your views on coercion versus secession; as you can imagine from what I wrote above I personally believe that such minority-chain-hostile difficulty adjustment algorithms are bad.The second edge case is that if the disparity is very large, the large chain can 51% attack the smaller chain. Even in the case of an ETH/ETC split with a 10:1 ratio, this has not happened; so it is certainly not a given. However, it is always a possibility if miners on the dominant chain prefer coercion to allowing secession and act on these values.Next, let's look at strictly expanding hard forks. In an SEHF, there is the property that the non-forked chain is valid under the forked rules, and so if the fork has a lower price than the non-forked chain, it will have less hashpower than the non-forked chain, and so the non-forked chain will end up being accepted as the longest chain by both original-client and forked-client rules - and so the forked chain "will be annihilated".There is an argument that there is thus a strong inherent bias against such a fork succeeding, as the possibility that the forked chain will get annihiliated will be baked into the price, pushing the price lower, making it even more likely that the chain will be annihilated... This argument to me seems strong, and so it is a very good reason to make any contentious hard fork bilateral rather than strictly expanding.Bitcoin Unlimited developers suggest dealing with this problem by making the hard fork bilateral manually after it happens, but a better choice would be to make the bilaterality built-in; for example, in the bitcoin case, one can add a rule to ban some unused opcode, and then make a transaction containing that opcode on the non-forked chain, so that under the forked rules the non-forked chain will from then on be considered forever invalid. In the Ethereum case, because of various details about how state calculation works, nearly all hard forks are bilateral almost automatically. Other chains may have different properties depending on their architecture.The last type of fork that was mentioned above is the user-activated soft fork. In a UASF, users turn on the soft fork rules without bothering to get consensus from miners; miners are expected to simply fall in line out of economic interest. If many users do not go along with the UASF, then there will be a coin split, and this will lead to a scenario identical to the strictly expanding hard fork, except - and this is the really clever and devious part of the concept - the same "risk of annihilation" pressure that strongly disfavors the forked chain in a strictly expanding hard fork instead strongly favors the forked chain in a UASF. Even though a UASF is opt-in, it uses economic asymmetry in order to bias itself toward success (though the bias is not absolute; if a UASF is decidedly unpopular then it will not succeed and will simply lead to a chain split).However, UASFs are a dangerous game. For example, let us suppose that the developers of a project want to make a UASF patch that converts an unused opcode that previously accepted all transactions into an opcode that only accepts transactions that comply with the rules of some cool new feature, though one that is politically or technically controversial and miners dislike. Miners have a clever and devious way to fight back: they can unilaterally implement a miner-activated soft fork that makes all transactions using the feature created by the soft fork always fail.Now, we have three rulesets:The original rules where opcode X is always valid. The rules where opcode X is only valid if the rest of the transaction complies with the new rules The rules where opcode X is always invalid. Note that (2) is a soft-fork with respect to (1), and (3) is a soft-fork with respect to (2). Now, there is strong economic pressure in favor of (3), and so the soft-fork fails to accomplish its objective.The conclusion is this. Soft forks are a dangerous game, and they become even more dangerous if they are contentious and miners start fighting back. Strictly expanding hard forks are also a dangerous game. Miner-activated soft forks are coercive; user-activated soft forks are less coercive, though still quite coercive because of the economic pressure, and they also have their dangers. If you really want to make a contentious change, and have decided that the high social costs of doing so are worth it, just do a clean bilateral hard fork, spend some time to add some proper replay protection, and let the market sort it out.

A Note On Charity Through Marginal Price Discrimination A Note On Charity Through Marginal Price Discrimination2017 Mar 11 See all posts A Note On Charity Through Marginal Price Discrimination Updated 2018-07-28. See end note.The following is an interesting idea that I had two years ago that I personally believe has promise and could be easily implemented in the context of a blockchain ecosystem, though if desired it could certainly also be implemented with more traditional technologies (blockchains would help get the scheme network effects by putting the core logic on a more neutral platform).Suppose that you are a restaurant selling sandwiches, and you ordinarily sell sandwiches for $7.50. Why did you choose to sell them for $7.50, and not $7.75 or $7.25? It clearly can't be the case that the cost of production is exactly $7.49999, as in that case you would be making no profit, and would not be able to cover fixed costs; hence, in most normal situations you would still be able to make some profit if you sold at $7.25 or $7.75, though less. Why less at $7.25? Because the price is lower. Why less at $7.75? Because you get fewer customers. It just so happens that $7.50 is the point at which the balance between those two factors is optimal for you. Notice one consequence of this: if you make a slight distortion to the optimal price, then even compared to the magnitude of the distortion the losses that you face are minimal. If you raise prices by 1%, from $7.50 to $7.575, then your profit declines from $6750 to $6733.12 - a tiny 0.25% reduction. And that's profit - if you had instead donated 1% of the price of each sandwich, it would have reduced your profit by 5%. The smaller the distortion the more favorable the ratio: raising prices by 0.2% only cuts your profits down by 0.01%.Now, you could argue that stores are not perfectly rational, and not perfectly informed, and so they may not actually be charging at optimal prices, all factors considered. However, if you don't know what direction the deviation is in for any given store, then even still, in expectation, the scheme works the same way - except instead of losing $17 it's more like flipping a coin where half the time you gain $50 and half the time you lose $84. Furthermore, in the more complex scheme that we will describe later, we'll be adjusting prices in both directions simultaneously, and so there will not even be any extra risk - no matter how correct or incorrect the original price was, the scheme will give you a predictable small net loss.Also, the above example was one where marginal costs are high, and customers are picky about prices - in the above model, charging $9 would have netted you no customers at all. In a situation where marginal costs are much lower, and customers are less price-sensitive, the losses from raising or lowering prices would be even lower.So what is the point of all this? Well, suppose that our sandwich shop changes its policy: it sells sandwiches for $7.55 to the general public, but lowers the prices to $7.35 for people who volunteered in some charity that maintains some local park (say, this is 25% of the population). The store's new profit is \(\$6682.5 \cdot 0.25+\$6742.5 \cdot 0.75=\$6727.5\) (that's a $22.5 loss), but the result is that you are now paying all 4500 of your customers 20 cents each to volunteer at that charity - an incentive size of $900 (if you just count the customers who actually do volunteer, $225). So the store loses a bit, but gets a huge amount of leverage, de-facto contributing at least $225 depending on how you measure it for a cost of only $22.5. Now, what we can start to do is build up an ecosystem of "stickers", which are non-transferable digital "tokens" that organizations hand out to people who they think are contributing to worthy causes. Tokens could be organized by category (eg. poverty relief, science research, environmental, local community projects, open source software development, writing good blogs), and merchants would be free to charge marginally lower prices to holders of the tokens that represent whatever causes they personally approve of.The next stage is to make the scheme recursive - being or working for a merchant that offers lower prices to holders of green stickers is itself enough to merit you a green sticker, albeit one that is of lower potency and gives you a lower discount. This way, if an entire community approves of a particular cause, it may actually be profit-maximizing to start offering discounts for the associated sticker, and so economic and social pressure will maintain a certain level of spending and participation toward the cause in a stable equilibrium.As far as implementation goes, this requires:A standard for stickers, including wallets where people can hold stickers Payment systems that have support for charging lower prices to sticker holders included At least a few sticker-issuing organizations (the lowest overhead is likely to be issuing stickers for charity donations, and for easily verifiable online content, eg. open source software and blogs) So this is something that can certainly be bootstrapped within a small community and user base and then let to grow over time.Update 2017.03.14: here is an economic model/simulation showing the above implemented as a Python script.Update 2018.07.28: after discussions with others (Glen Weyl and several Reddit commenters), I realized a few extra things about this mechanism, some encouraging and some worrying:The above mechanism could be used not just by charities, but also by centralized corporate actors. For example, a large corporation could offer a bribe of $40 to any store that offers the 20-cent discount to customers of its products, gaining additional revenue much higher than $40. So it's empowering but potentially dangerous in the wrong hands... (I have not researched it but I'm sure this kind of technique is used in various kinds of loyalty programs already) The above mechanism has the property that a merchant can "donate" \(\$x\) to charity at a cost of \(\$x^\) (note: \(x^