heyuan 发布的文章 - 六币之门

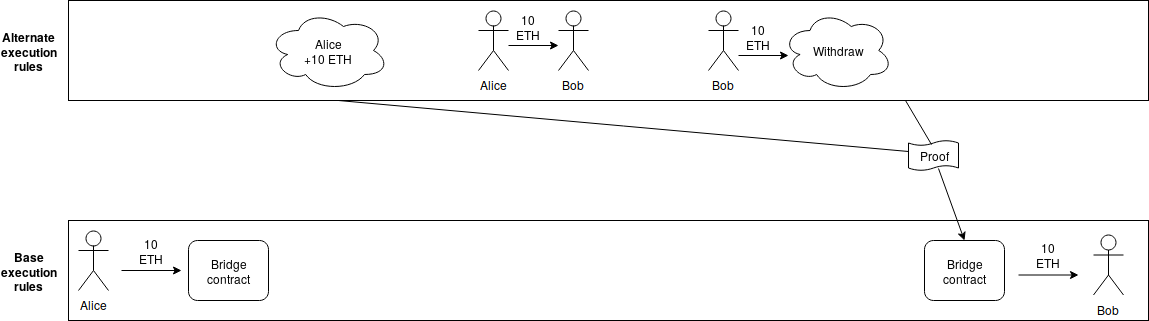
Layer 1 Should Be Innovative in the Short Term but Less in the Long Term Layer 1 Should Be Innovative in the Short Term but Less in the Long Term2018 Aug 26 See all posts Layer 1 Should Be Innovative in the Short Term but Less in the Long Term See update 2018-08-29One of the key tradeoffs in blockchain design is whether to build more functionality into base-layer blockchains themselves ("layer 1"), or to build it into protocols that live on top of the blockchain, and can be created and modified without changing the blockchain itself ("layer 2"). The tradeoff has so far shown itself most in the scaling debates, with block size increases (and sharding) on one side and layer-2 solutions like Plasma and channels on the other, and to some extent blockchain governance, with loss and theft recovery being solvable by either the DAO fork or generalizations thereof such as EIP 867, or by layer-2 solutions such as Reversible Ether (RETH). So which approach is ultimately better? Those who know me well, or have seen me out myself as a dirty centrist, know that I will inevitably say "some of both". However, in the longer term, I do think that as blockchains become more and more mature, layer 1 will necessarily stabilize, and layer 2 will take on more and more of the burden of ongoing innovation and change.There are several reasons why. The first is that layer 1 solutions require ongoing protocol change to happen at the base protocol layer, base layer protocol change requires governance, and it has still not been shown that, in the long term, highly "activist" blockchain governance can continue without causing ongoing political uncertainty or collapsing into centralization.To take an example from another sphere, consider Moxie Marlinspike's defense of Signal's centralized and non-federated nature. A document by a company defending its right to maintain control over an ecosystem it depends on for its key business should of course be viewed with massive grains of salt, but one can still benefit from the arguments. Quoting:One of the controversial things we did with Signal early on was to build it as an unfederated service. Nothing about any of the protocols we've developed requires centralization; it's entirely possible to build a federated Signal Protocol-based messenger, but I no longer believe that it is possible to build a competitive federated messenger at all.And:Their retort was "that's dumb, how far would the internet have gotten without interoperable protocols defined by 3rd parties?" I thought about it. We got to the first production version of IP, and have been trying for the past 20 years to switch to a second production version of IP with limited success. We got to HTTP version 1.1 in 1997, and have been stuck there until now. Likewise, SMTP, IRC, DNS, XMPP, are all similarly frozen in time circa the late 1990s. To answer his question, that's how far the internet got. It got to the late 90s. That has taken us pretty far, but it's undeniable that once you federate your protocol, it becomes very difficult to make changes. And right now, at the application level, things that stand still don't fare very well in a world where the ecosystem is moving ... So long as federation means stasis while centralization means movement, federated protocols are going to have trouble existing in a software climate that demands movement as it does today.At this point in time, and in the medium term going forward, it seems clear that decentralized application platforms, cryptocurrency payments, identity systems, reputation systems, decentralized exchange mechanisms, auctions, privacy solutions, programming languages that support privacy solutions, and most other interesting things that can be done on blockchains are spheres where there will continue to be significant and ongoing innovation. Decentralized application platforms often need continued reductions in confirmation time, payments need fast confirmations, low transaction costs, privacy, and many other built-in features, exchanges are appearing in many shapes and sizes including on-chain automated market makers, frequent batch auctions, combinatorial auctions and more. Hence, "building in" any of these into a base layer blockchain would be a bad idea, as it would create a high level of governance overhead as the platform would have to continually discuss, implement and coordinate newly discovered technical improvements. For the same reason federated messengers have a hard time getting off the ground without re-centralizing, blockchains would also need to choose between adopting activist governance, with the perils that entails, and falling behind newly appearing alternatives.Even Ethereum's limited level of application-specific functionality, precompiles, has seen some of this effect. Less than a year ago, Ethereum adopted the Byzantium hard fork, including operations to facilitate elliptic curve operations needed for ring signatures, ZK-SNARKs and other applications, using the alt-bn128 curve. Now, Zcash and other blockchains are moving toward BLS-12-381, and Ethereum would need to fork again to catch up. In part to avoid having similar problems in the future, the Ethereum community is looking to upgrade the EVM to E-WASM, a virtual machine that is sufficiently more efficient that there is far less need to incorporate application-specific precompiles.But there is also a second argument in favor of layer 2 solutions, one that does not depend on speed of anticipated technical development: sometimes there are inevitable tradeoffs, with no single globally optimal solution. This is less easily visible in Ethereum 1.0-style blockchains, where there are certain models that are reasonably universal (eg. Ethereum's account-based model is one). In sharded blockchains, however, one type of question that does not exist in Ethereum today crops up: how to do cross-shard transactions? That is, suppose that the blockchain state has regions A and B, where few or no nodes are processing both A and B. How does the system handle transactions that affect both A and B?The current answer involves asynchronous cross-shard communication, which is sufficient for transferring assets and some other applications, but insufficient for many others. Synchronous operations (eg. to solve the train and hotel problem) can be bolted on top with cross-shard yanking, but this requires multiple rounds of cross-shard interaction, leading to significant delays. We can solve these problems with a synchronous execution scheme, but this comes with several tradeoffs:The system cannot process more than one transaction for the same account per block Transactions must declare in advance what shards and addresses they affect There is a high risk of any given transaction failing (and still being required to pay fees!) if the transaction is only accepted in some of the shards that it affects but not others It seems very likely that a better scheme can be developed, but it would be more complex, and may well have limitations that this scheme does not. There are known results preventing perfection; at the very least, Amdahl's law puts a hard limit on the ability of some applications and some types of interaction to process more transactions per second through parallelization.So how do we create an environment where better schemes can be tested and deployed? The answer is an idea that can be credited to Justin Drake: layer 2 execution engines. Users would be able to send assets into a "bridge contract", which would calculate (using some indirect technique such as interactive verification or ZK-SNARKs) state roots using some alternative set of rules for processing the blockchain (think of this as equivalent to layer-two "meta-protocols" like Mastercoin/OMNI and Counterparty on top of Bitcoin, except because of the bridge contract these protocols would be able to handle assets whose "base ledger" is defined on the underlying protocol), and which would process withdrawals if and only if the alternative ruleset generates a withdrawal request. Note that anyone can create a layer 2 execution engine at any time, different users can use different execution engines, and one can switch from one execution engine to any other, or to the base protocol, fairly quickly. The base blockchain no longer has to worry about being an optimal smart contract processing engine; it need only be a data availability layer with execution rules that are quasi-Turing-complete so that any layer 2 bridge contract can be built on top, and that allow basic operations to carry state between shards (in fact, only ETH transfers being fungible across shards is sufficient, but it takes very little effort to also allow cross-shard calls, so we may as well support them), but does not require complexity beyond that. Note also that layer 2 execution engines can have different state management rules than layer 1, eg. not having storage rent; anything goes, as it's the responsibility of the users of that specific execution engine to make sure that it is sustainable, and if they fail to do so the consequences are contained to within the users of that particular execution engine.In the long run, layer 1 would not be actively competing on all of these improvements; it would simply provide a stable platform for the layer 2 innovation to happen on top. Does this mean that, say, sharding is a bad idea, and we should keep the blockchain size and state small so that even 10 year old computers can process everyone's transactions? Absolutely not. Even if execution engines are something that gets partially or fully moved to layer 2, consensus on data ordering and availability is still a highly generalizable and necessary function; to see how difficult layer 2 execution engines are without layer 1 scalable data availability consensus, see the difficulties in Plasma research, and its difficulty of naturally extending to fully general purpose blockchains, for an example. And if people want to throw a hundred megabytes per second of data into a system where they need consensus on availability, then we need a hundred megabytes per second of data availability consensus.Additionally, layer 1 can still improve on reducing latency; if layer 1 is slow, the only strategy for achieving very low latency is state channels, which often have high capital requirements and can be difficult to generalize. State channels will always beat layer 1 blockchains in latency as state channels require only a single network message, but in those cases where state channels do not work well, layer 1 blockchains can still come closer than they do today.Hence, the other extreme position, that blockchain base layers can be truly absolutely minimal, and not bother with either a quasi-Turing-complete execution engine or scalability to beyond the capacity of a single node, is also clearly false; there is a certain minimal level of complexity that is required for base layers to be powerful enough for applications to build on top of them, and we have not yet reached that level. Additional complexity is needed, though it should be chosen very carefully to make sure that it is maximally general purpose, and not targeted toward specific applications or technologies that will go out of fashion in two years due to loss of interest or better alternatives.And even in the future base layers will need to continue to make some upgrades, especially if new technologies (eg. STARKs reaching higher levels of maturity) allow them to achieve stronger properties than they could before, though developers today can take care to make base layer platforms maximally forward-compatible with such potential improvements. So it will continue to be true that a balance between layer 1 and layer 2 improvements is needed to continue improving scalability, privacy and versatility, though layer 2 will continue to take up a larger and larger share of the innovation over time.Update 2018.08.29: Justin Drake pointed out to me another good reason why some features may be best implemented on layer 1: those features are public goods, and so could not be efficiently or reliably funded with feature-specific use fees, and hence are best paid for by subsidies paid out of issuance or burned transaction fees. One possible example of this is secure random number generation, and another is generation of zero knowledge proofs for more efficient client validation of correctness of various claims about blockchain contents or state.

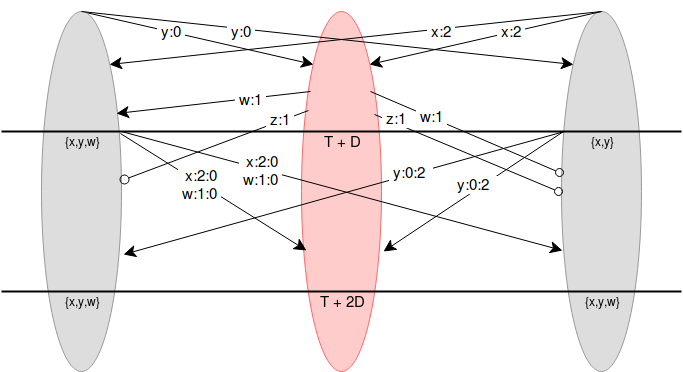
A Guide to 99% Fault Tolerant Consensus A Guide to 99% Fault Tolerant Consensus2018 Aug 07 See all posts A Guide to 99% Fault Tolerant Consensus Special thanks to Emin Gun Sirer for reviewWe've heard for a long time that it's possible to achieve consensus with 50% fault tolerance in a synchronous network where messages broadcasted by any honest node are guaranteed to be received by all other honest nodes within some known time period (if an attacker has more than 50%, they can perform a "51% attack", and there's an analogue of this for any algorithm of this type). We've also heard for a long time that if you want to relax the synchrony assumption, and have an algorithm that's "safe under asynchrony", the maximum achievable fault tolerance drops to 33% (PBFT, Casper FFG, etc all fall into this category). But did you know that if you add even more assumptions (specifically, you require observers, ie. users that are not actively participating in the consensus but care about its output, to also be actively watching the consensus, and not just downloading its output after the fact), you can increase fault tolerance all the way to 99%?This has in fact been known for a long time; Leslie Lamport's famous 1982 paper "The Byzantine Generals Problem" (link here) contains a description of the algorithm. The following will be my attempt to describe and reformulate the algorithm in a simplified form.Suppose that there are \(N\) consensus-participating nodes, and everyone agrees who these nodes are ahead of time (depending on context, they could have been selected by a trusted party or, if stronger decentralization is desired, by some proof of work or proof of stake scheme). We label these nodes \(0 ...N-1\). Suppose also that there is a known bound \(D\) on network latency plus clock disparity (eg. \(D\) = 8 seconds). Each node has the ability to publish a value at time \(T\) (a malicious node can of course propose values earlier or later than \(T\)). All nodes wait \((N-1) \cdot D\) seconds, running the following process. Define \(x : i\) as "the value \(x\) signed by node \(i\)", \(x : i : j\) as "the value \(x\) signed by \(i\), and that value and signature together signed by \(j\)", etc. The proposals published in the first stage will be of the form \(v: i\) for some \(v\) and \(i\), containing the signature of the node that proposed it.If a validator \(i\) receives some message \(v : i[1] : ... : i[k]\), where \(i[1] ... i[k]\) is a list of indices that have (sequentially) signed the message already (just \(v\) by itself would count as \(k=0\), and \(v:i\) as \(k=1\)), then the validator checks that (i) the time is less than \(T + k \cdot D\), and (ii) they have not yet seen a valid message containing \(v\); if both checks pass, they publish \(v : i[1] : ... : i[k] : i\).At time \(T + (N-1) \cdot D\), nodes stop listening. At this point, there is a guarantee that honest nodes have all "validly seen" the same set of values. Node 1 (red) is malicious, and nodes 0 and 2 (grey) are honest. At the start, the two honest nodes make their proposals \(y\) and \(x\), and the attacker proposes both \(w\) and \(z\) late. \(w\) reaches node 0 on time but not node 2, and \(z\) reaches neither node on time. At time \(T + D\), nodes 0 and 2 rebroadcast all values they've seen that they have not yet broadcasted, but add their signatures on (\(x\) and \(w\) for node 0, \(y\) for node 2). Both honest nodes saw \(\).If the problem demands choosing one value, they can use some "choice" function to pick a single value out of the values they have seen (eg. they take the one with the lowest hash). The nodes can then agree on this value.Now, let's explore why this works. What we need to prove is that if one honest node has seen a particular value (validly), then every other honest node has also seen that value (and if we prove this, then we know that all honest nodes have seen the same set of values, and so if all honest nodes are running the same choice function, they will choose the same value). Suppose that any honest node receives a message \(v : i[1] : ... : i[k]\) that they perceive to be valid (ie. it arrives before time \(T + k \cdot D\)). Suppose \(x\) is the index of a single other honest node. Either \(x\) is part of \(\) or it is not.In the first case (say \(x = i[j]\) for this message), we know that the honest node \(x\) had already broadcasted that message, and they did so in response to a message with \(j-1\) signatures that they received before time \(T + (j-1) \cdot D\), so they broadcast their message at that time, and so the message must have been received by all honest nodes before time \(T + j \cdot D\). In the second case, since the honest node sees the message before time \(T + k \cdot D\), then they will broadcast the message with their signature and guarantee that everyone, including \(x\), will see it before time \(T + (k+1) \cdot D\). Notice that the algorithm uses the act of adding one's own signature as a kind of "bump" on the timeout of a message, and it's this ability that guarantees that if one honest node saw a message on time, they can ensure that everyone else sees the message on time as well, as the definition of "on time" increments by more than network latency with every added signature.In the case where one node is honest, can we guarantee that passive observers (ie. non-consensus-participating nodes that care about knowing the outcome) can also see the outcome, even if we require them to be watching the process the whole time? With the scheme as written, there's a problem. Suppose that a commander and some subset of \(k\) (malicious) validators produce a message \(v : i[1] : .... : i[k]\), and broadcast it directly to some "victims" just before time \(T + k \cdot D\). The victims see the message as being "on time", but when they rebroadcast it, it only reaches all honest consensus-participating nodes after \(T + k \cdot D\), and so all honest consensus-participating nodes reject it. But we can plug this hole. We require \(D\) to be a bound on two times network latency plus clock disparity. We then put a different timeout on observers: an observer accepts \(v : i[1] : .... : i[k]\) before time \(T + (k - 0.5) \cdot D\). Now, suppose an observer sees a message an accepts it. They will be able to broadcast it to an honest node before time \(T + k \cdot D\), and the honest node will issue the message with their signature attached, which will reach all other observers before time \(T + (k + 0.5) \cdot D\), the timeout for messages with \(k+1\) signatures. Retrofitting onto other consensus algorithmsThe above could theoretically be used as a standalone consensus algorithm, and could even be used to run a proof-of-stake blockchain. The validator set of round \(N+1\) of the consensus could itself be decided during round \(N\) of the consensus (eg. each round of a consensus could also accept "deposit" and "withdraw" transactions, which if accepted and correctly signed would add or remove validators into the next round). The main additional ingredient that would need to be added is a mechanism for deciding who is allowed to propose blocks (eg. each round could have one designated proposer). It could also be modified to be usable as a proof-of-work blockchain, by allowing consensus-participating nodes to "declare themselves" in real time by publishing a proof of work solution on top of their public key at th same time as signing a message with it.However, the synchrony assumption is very strong, and so we would like to be able to work without it in the case where we don't need more than 33% or 50% fault tolerance. There is a way to accomplish this. Suppose that we have some other consensus algorithm (eg. PBFT, Casper FFG, chain-based PoS) whose output can be seen by occasionally-online observers (we'll call this the threshold-dependent consensus algorithm, as opposed to the algorithm above, which we'll call the latency-dependent consensus algorithm). Suppose that the threshold-dependent consensus algorithm runs continuously, in a mode where it is constantly "finalizing" new blocks onto a chain (ie. each finalized value points to some previous finalized value as a "parent"; if there's a sequence of pointers \(A \rightarrow ... \rightarrow B\), we'll call \(A\) a descendant of \(B\)).We can retrofit the latency-dependent algorithm onto this structure, giving always-online observers access to a kind of "strong finality" on checkpoints, with fault tolerance ~95% (you can push this arbitrarily close to 100% by adding more validators and requiring the process to take longer).Every time the time reaches some multiple of 4096 seconds, we run the latency-dependent algorithm, choosing 512 random nodes to participate in the algorithm. A valid proposal is any valid chain of values that were finalized by the threshold-dependent algorithm. If a node sees some finalized value before time \(T + k \cdot D\) (\(D\) = 8 seconds) with \(k\) signatures, it accepts the chain into its set of known chains and rebroadcasts it with its own signature added; observers use a threshold of \(T + (k - 0.5) \cdot D\) as before.The "choice" function used at the end is simple:Finalized values that are not descendants of what was already agreed to be a finalized value in the previous round are ignored Finalized values that are invalid are ignored To choose between two valid finalized values, pick the one with the lower hash If 5% of validators are honest, there is only a roughly 1 in 1 trillion chance that none of the 512 randomly selected nodes will be honest, and so as long as the network latency plus clock disparity is less than \(\frac\) the above algorithm will work, correctly coordinating nodes on some single finalized value, even if multiple conflicting finalized values are presented because the fault tolerance of the threshold-dependent algorithm is broken.If the fault tolerance of the threshold-dependent consensus algorithm is met (usually 50% or 67% honest), then the threshold-dependent consensus algorithm will either not finalize any new checkpoints, or it will finalize new checkpoints that are compatible with each other (eg. a series of checkpoints where each points to the previous as a parent), so even if network latency exceeds \(\frac\) (or even \(D\)), and as a result nodes participating in the latency-dependent algorithm disagree on which value they accept, the values they accept are still guaranteed to be part of the same chain and so there is no actual disagreement. Once latency recovers back to normal in some future round, the latency-dependent consensus will get back "in sync".If the assumptions of both the threshold-dependent and latency-dependent consensus algorithms are broken at the same time (or in consecutive rounds), then the algorithm can break down. For example, suppose in one round, the threshold-dependent consensus finalizes \(Z \rightarrow Y \rightarrow X\) and the latency-dependent consensus disagrees between \(Y\) and \(X\), and in the next round the threshold-dependent consensus finalizes a descendant \(W\) of \(X\) which is not a descendant of \(Y\); in the latency-dependent consensus, the nodes who agreed \(Y\) will not accept \(W\), but the nodes that agreed \(X\) will. However, this is unavoidable; the impossibility of safe-under-asynchrony consensus with more than \(\frac\) fault tolerance is a well known result in Byzantine fault tolerance theory, as is the impossibility of more than \(\frac\) fault tolerance even allowing synchrony assumptions but assuming offline observers.

STARKs, Part 3: Into the Weeds STARKs, Part 3: Into the Weeds2018 Jul 21 See all posts STARKs, Part 3: Into the Weeds Special thanks to Eli ben Sasson for his kind assistance, as usual. Special thanks to Chih-Cheng Liang and Justin Drake for review, and to Ben Fisch for suggesting the reverse MIMC technique for a VDF (paper here)Trigger warning: math and lots of pythonAs a followup to Part 1 and Part 2 of this series, this post will cover what it looks like to actually implement a STARK, complete with an implementation in python. STARKs ("Scalable Transparent ARgument of Knowledge" are a technique for creating a proof that \(f(x)=y\) where \(f\) may potentially take a very long time to calculate, but where the proof can be verified very quickly. A STARK is "doubly scalable": for a computation with \(t\) steps, it takes roughly \(O(t \cdot \log)\) steps to produce a proof, which is likely optimal, and it takes ~\(O(\log^2)\) steps to verify, which for even moderately large values of \(t\) is much faster than the original computation. STARKs can also have a privacy-preserving "zero knowledge" property, though the use case we will apply them to here, making verifiable delay functions, does not require this property, so we do not need to worry about it.First, some disclaimers:This code has not been thoroughly audited; soundness in production use cases is not guaranteed This code is very suboptimal (it's written in Python, what did you expect) STARKs "in real life" (ie. as implemented in Eli and co's production implementations) tend to use binary fields and not prime fields for application-specific efficiency reasons; however, they do stress in their writings the prime field-based approach to STARKs described here is legitimate and can be used There is no "one true way" to do a STARK. It's a broad category of cryptographic and mathematical constructs, with different setups optimal for different applications and constant ongoing research to reduce prover and verifier complexity and improve soundness. This article absolutely expects you to know how modular arithmetic and prime fields work, and be comfortable with the concepts of polynomials, interpolation and evaluation. If you don't, go back to Part 2, and also this earlier post on quadratic arithmetic programs Now, let's get to it.MIMCHere is the function we'll be doing a STARK of:def mimc(inp, steps, round_constants): start_time = time.time() for i in range(steps-1): inp = (inp**3 + round_constants[i % len(round_constants)]) % modulus print("MIMC computed in%.4fsec" % (time.time() - start_time)) return inpWe choose MIMC (see paper) as the example because it is both (i) simple to understand and (ii) interesting enough to be useful in real life. The function can be viewed visually as follows: Note: in many discussions of MIMC, you will typically see XOR used instead of +; this is because MIMC is typically done over binary fields, where addition is XOR; here we are doing it over prime fields.In our example, the round constants will be a relatively small list (eg. 64 items) that gets cycled through over and over again (that is, after k[64] it loops back to using k[1]).MIMC with a very large number of rounds, as we're doing here, is useful as a verifiable delay function - a function which is difficult to compute, and particularly non-parallelizable to compute, but relatively easy to verify. MIMC by itself achieves this property to some extent because MIMC can be computed "backward" (recovering the "input" from its corresponding "output"), but computing it backward takes about 100 times longer to compute than the forward direction (and neither direction can be significantly sped up by parallelization). So you can think of computing the function in the backward direction as being the act of "computing" the non-parallelizable proof of work, and computing the function in the forward direction as being the process of "verifying" it. \(x \rightarrow x^\) gives the inverse of \(x \rightarrow x^3\); this is true because of Fermat's Little Theorem, a theorem that despite its supposed littleness is arguably much more important to mathematics than Fermat's more famous "Last Theorem".What we will try to achieve here is to make verification much more efficient by using a STARK - instead of the verifier having to run MIMC in the forward direction themselves, the prover, after completing the computation in the "backward direction", would compute a STARK of the computation in the "forward direction", and the verifier would simply verify the STARK. The hope is that the overhead of computing a STARK can be less than the difference in speed running MIMC forwards relative to backwards, so a prover's time would still be dominated by the initial "backward" computation, and not the (highly parallelizable) STARK computation. Verification of a STARK can be relatively fast (in our python implementation, ~0.05-0.3 seconds), no matter how long the original computation is.All calculations are done modulo \(2^ - 351 \cdot 2^ + 1\); we are using this prime field modulus because it is the largest prime below \(2^\) whose multiplicative group contains an order \(2^\) subgroup (that is, there's a number \(g\) such that successive powers of \(g\) modulo this prime loop around back to \(1\) after exactly \(2^\) cycles), and which is of the form \(6k+5\). The first property is necessary to make sure that our efficient versions of the FFT and FRI algorithms can work, and the second ensures that MIMC actually can be computed "backwards" (see the use of \(x \rightarrow x^\) above).Prime field operationsWe start off by building a convenience class that does prime field operations, as well as operations with polynomials over prime fields. The code is here. First some trivial bits:class PrimeField(): def __init__(self, modulus): # Quick primality test assert pow(2, modulus, modulus) == 2 self.modulus = modulus def add(self, x, y): return (x+y) % self.modulus def sub(self, x, y): return (x-y) % self.modulus def mul(self, x, y): return (x*y) % self.modulusAnd the Extended Euclidean Algorithm for computing modular inverses (the equivalent of computing \(\frac\) in a prime field):# Modular inverse using the extended Euclidean algorithm def inv(self, a): if a == 0: return 0 lm, hm = 1, 0 low, high = a % self.modulus, self.modulus while low > 1: r = high//low nm, new = hm-lm*r, high-low*r lm, low, hm, high = nm, new, lm, low return lm % self.modulusThe above algorithm is relatively expensive; fortunately, for the special case where we need to do many modular inverses, there's a simple mathematical trick that allows us to compute many inverses, called Montgomery batch inversion: Using Montgomery batch inversion to compute modular inverses. Inputs purple, outputs green, multiplication gates black; the red square is the only modular inversion.The code below implements this algorithm, with some slightly ugly special case logic so that if there are zeroes in the set of what we are inverting, it sets their inverse to 0 and moves along.def multi_inv(self, values): partials = [1] for i in range(len(values)): partials.append(self.mul(partials[-1], values[i] or 1)) inv = self.inv(partials[-1]) outputs = [0] * len(values) for i in range(len(values), 0, -1): outputs[i-1] = self.mul(partials[i-1], inv) if values[i-1] else 0 inv = self.mul(inv, values[i-1] or 1) return outputsThis batch inverse algorithm will prove important later on, when we start dealing with dividing sets of evaluations of polynomials.Now we move on to some polynomial operations. We treat a polynomial as an array, where element \(i\) is the \(i\)th degree term (eg. \(x^ + 2x + 1\) becomes [1, 2, 0, 1]). Here's the operation of evaluating a polynomial at one point:# Evaluate a polynomial at a point def eval_poly_at(self, p, x): y = 0 power_of_x = 1 for i, p_coeff in enumerate(p): y += power_of_x * p_coeff power_of_x = (power_of_x * x) % self.modulus return y % self.modulusChallengeWhat is the output of f.eval_poly_at([4, 5, 6], 2) if the modulus is 31?Mouseover below for answer\(6 \cdot 2^ + 5 \cdot 2 + 4 = 38, 38 \bmod 31 = 7\).There is also code for adding, subtracting, multiplying and dividing polynomials; this is textbook long addition/subtraction/multiplication/division. The one non-trivial thing is Lagrange interpolation, which takes as input a set of x and y coordinates, and returns the minimal polynomial that passes through all of those points (you can think of it as being the inverse of polynomial evaluation):# Build a polynomial that returns 0 at all specified xs def zpoly(self, xs): root = [1] for x in xs: root.insert(0, 0) for j in range(len(root)-1): root[j] -= root[j+1] * x return [x % self.modulus for x in root] def lagrange_interp(self, xs, ys): # Generate master numerator polynomial, eg. (x - x1) * (x - x2) * ... * (x - xn) root = self.zpoly(xs) # Generate per-value numerator polynomials, eg. for x=x2, # (x - x1) * (x - x3) * ... * (x - xn), by dividing the master # polynomial back by each x coordinate nums = [self.div_polys(root, [-x, 1]) for x in xs] # Generate denominators by evaluating numerator polys at each x denoms = [self.eval_poly_at(nums[i], xs[i]) for i in range(len(xs))] invdenoms = self.multi_inv(denoms) # Generate output polynomial, which is the sum of the per-value numerator # polynomials rescaled to have the right y values b = [0 for y in ys] for i in range(len(xs)): yslice = self.mul(ys[i], invdenoms[i]) for j in range(len(ys)): if nums[i][j] and ys[i]: b[j] += nums[i][j] * yslice return [x % self.modulus for x in b]See the "M of N" section of this article for a description of the math. Note that we also have special-case methods lagrange_interp_4 and lagrange_interp_2 to speed up the very frequent operations of Lagrange interpolation of degree \(< 2\) and degree \(< 4\) polynomials.Fast Fourier TransformsIf you read the above algorithms carefully, you might notice that Lagrange interpolation and multi-point evaluation (that is, evaluating a degree \(< N\) polynomial at \(N\) points) both take quadratic time to execute, so for example doing a Lagrange interpolation of one thousand points takes a few million steps to execute, and a Lagrange interpolation of one million points takes a few trillion. This is an unacceptably high level of inefficiency, so we will use a more efficient algorithm, the Fast Fourier Transform.The FFT only takes \(O(n \cdot log(n))\) time (ie. ~10,000 steps for 1,000 points, ~20 million steps for 1 million points), though it is more restricted in scope; the x coordinates must be a complete set of roots of unity of some order \(N = 2^\). That is, if there are \(N\) points, the x coordinates must be successive powers \(1, p, p^, p^\)... of some \(p\) where \(p^ = 1\). The algorithm can, surprisingly enough, be used for multi-point evaluation or interpolation, with one small parameter tweak.Challenge Find a 16th root of unity mod 337 that is not an 8th root of unity.Mouseover below for answer59, 146, 30, 297, 278, 191, 307, 40You could have gotten this list by doing something like [print(x) for x in range(337) if pow(x, 16, 337) == 1 and pow(x, 8, 337) != 1], though there is a smarter way that works for much larger moduluses: first, identify a single primitive root mod 337 (that is, not a perfect square), by looking for a value x such that pow(x, 336 // 2, 337) != 1 (these are easy to find; one answer is 5), and then taking the (336 / 16)'th power of it.Here's the algorithm (in a slightly simplified form; see code here for something slightly more optimized):def fft(vals, modulus, root_of_unity): if len(vals) == 1: return vals L = fft(vals[::2], modulus, pow(root_of_unity, 2, modulus)) R = fft(vals[1::2], modulus, pow(root_of_unity, 2, modulus)) o = [0 for i in vals] for i, (x, y) in enumerate(zip(L, R)): y_times_root = y*pow(root_of_unity, i, modulus) o[i] = (x+y_times_root) % modulus o[i+len(L)] = (x-y_times_root) % modulus return o def inv_fft(vals, modulus, root_of_unity): f = PrimeField(modulus) # Inverse FFT invlen = f.inv(len(vals)) return [(x*invlen) % modulus for x in fft(vals, modulus, f.inv(root_of_unity))]You can try running it on a few inputs yourself and check that it gives results that, when you use eval_poly_at on them, give you the answers you expect to get. For example:>>> fft.fft([3,1,4,1,5,9,2,6], 337, 85, inv=True) [46, 169, 29, 149, 126, 262, 140, 93] >>> f = poly_utils.PrimeField(337) >>> [f.eval_poly_at([46, 169, 29, 149, 126, 262, 140, 93], f.exp(85, i)) for i in range(8)] [3, 1, 4, 1, 5, 9, 2, 6]A Fourier transform takes as input [x[0] .... x[n-1]], and its goal is to output x[0] + x[1] + ... + x[n-1] as the first element, x[0] + x[1] * 2 + ... + x[n-1] * w**(n-1) as the second element, etc etc; a fast Fourier transform accomplishes this by splitting the data in half, doing an FFT on both halves, and then gluing the result back together. A diagram of how information flows through the FFT computation. Notice how the FFT consists of a "gluing" step followed by two copies of the FFT on two halves of the data, and so on recursively until you're down to one element.I recommend this for more intuition on how or why the FFT works and polynomial math in general, and this thread for some more specifics on DFT vs FFT, though be warned that most literature on Fourier transforms talks about Fourier transforms over real and complex numbers, not prime fields. If you find this too hard and don't want to understand it, just treat it as weird spooky voodoo that just works because you ran the code a few times and verified that it works, and you'll be fine too.Thank Goodness It's FRI-day (that's "Fast Reed-Solomon Interactive Oracle Proofs of Proximity")Reminder: now may be a good time to review and re-read Part 2Now, we'll get into the code for making a low-degree proof. To review, a low-degree proof is a (probabilistic) proof that at least some high percentage (eg. 80%) of a given set of values represent the evaluations of some specific polynomial whose degree is much lower than the number of values given. Intuitively, just think of it as a proof that "some Merkle root that we claim represents a polynomial actually does represent a polynomial, possibly with a few errors". As input, we have:A set of values that we claim are the evaluation of a low-degree polynomial A root of unity; the x coordinates at which the polynomial is evaluated are successive powers of this root of unity A value \(N\) such that we are proving the degree of the polynomial is strictly less than \(N\) The modulus Our approach is a recursive one, with two cases. First, if the degree is low enough, we just provide the entire list of values as a proof; this is the "base case". Verification of the base case is trivial: do an FFT or Lagrange interpolation or whatever else to interpolate the polynomial representing those values, and verify that its degree is \(< N\). Otherwise, if the degree is higher than some set minimum, we do the vertical-and-diagonal trick described at the bottom of Part 2.We start off by putting the values into a Merkle tree and using the Merkle root to select a pseudo-random x coordinate (special_x). We then calculate the "column":# Calculate the set of x coordinates xs = get_power_cycle(root_of_unity, modulus) column = [] for i in range(len(xs)//4): x_poly = f.lagrange_interp_4( [xs[i+len(xs)*j//4] for j in range(4)], [values[i+len(values)*j//4] for j in range(4)], ) column.append(f.eval_poly_at(x_poly, special_x))This packs a lot into a few lines of code. The broad idea is to re-interpret the polynomial \(P(x)\) as a polynomial \(Q(x, y)\), where \(P(x) = Q(x, x^4)\). If \(P\) has degree \(< N\), then \(P'(y) = Q(special\_x, y)\) will have degree \(< \frac\). Since we don't want to take the effort to actually compute \(Q\) in coefficient form (that would take a still-relatively-nasty-and-expensive FFT!), we instead use another trick. For any given value of \(x^\), there are 4 corresponding values of \(x\): \(x\), \(modulus - x\), and \(x\) multiplied by the two modular square roots of \(-1\). So we already have four values of \(Q(?, x^4)\), which we can use to interpolate the polynomial \(R(x) = Q(x, x^4)\), and from there calculate \(R(special\_x) = Q(special\_x, x^4) = P'(x^4)\). There are \(\frac\) possible values of \(x^\), and this lets us easily calculate all of them. A diagram from part 2; it helps to keep this in mind when understanding what's going on hereOur proof consists of some number (eg. 40) of random queries from the list of values of \(x^\) (using the Merkle root of the column as a seed), and for each query we provide Merkle branches of the five values of \(Q(?, x^4)\):m2 = merkelize(column) # Pseudo-randomly select y indices to sample # (m2[1] is the Merkle root of the column) ys = get_pseudorandom_indices(m2[1], len(column), 40) # Compute the Merkle branches for the values in the polynomial and the column branches = [] for y in ys: branches.append([mk_branch(m2, y)] + [mk_branch(m, y + (len(xs) // 4) * j) for j in range(4)])The verifier's job will be to verify that these five values actually do lie on the same degree \(< 4\) polynomial. From there, we recurse and do an FRI on the column, verifying that the column actually does have degree \(< \frac\). That really is all there is to FRI.As a challenge exercise, you could try creating low-degree proofs of polynomial evaluations that have errors in them, and see how many errors you can get away passing the verifier with (hint, you'll need to modify the prove_low_degree function; with the default prover, even one error will balloon up and cause verification to fail).The STARKReminder: now may be a good time to review and re-read Part 1Now, we get to the actual meat that puts all of these pieces together: def mk_mimc_proof(inp, steps, round_constants) (code here), which generates a proof of the execution result of running the MIMC function with the given input for some number of steps. First, some asserts:assert steps

On Radical Markets On Radical Markets2018 Apr 20 See all posts On Radical Markets Recently I had the fortune to have received an advance copy of Eric Posner and Glen Weyl's new book, Radical Markets, which could be best described as an interesting new way of looking at the subject that is sometimes called "political economy" - tackling the big questions of how markets and politics and society intersect. The general philosophy of the book, as I interpret it, can be expressed as follows. Markets are great, and price mechanisms are an awesome way of guiding the use of resources in society and bringing together many participants' objectives and information into a coherent whole. However, markets are socially constructed because they depend on property rights that are socially constructed, and there are many different ways that markets and property rights can be constructed, some of which are unexplored and potentially far better than what we have today. Contra doctrinaire libertarians, freedom is a high-dimensional design space.The book interests me for multiple reasons. First, although I spend most of my time in the blockchain/crypto space heading up the Ethereum project and in some cases providing various kinds of support to projects in the space, I do also have broader interests, of which the use of economics and mechanism design to make more open, free, egalitarian and efficient systems for human cooperation, including improving or replacing present-day corporations and governments, is a major one. The intersection of interests between the Ethereum community and Posner and Weyl's work is multifaceted and plentiful; Radical Markets dedicates an entire chapter to the idea of "markets for personal data", redefining the economic relationship between ourselves and services like Facebook, and well, look what the Ethereum community is working on: markets for personal data.Second, blockchains may well be used as a technical backbone for some of the solutions described in the book, and Ethereum-style smart contracts are ideal for the kinds of complex systems of property rights that the book explores. Third, the economic ideas and challenges that the book brings up are ideas that have also been explored, and will be continue to be explored, at great length by the blockchain community for its own purposes. Posner and Weyl's ideas often have the feature that they allow economic incentive alignment to serve as a substitute for subjective ad-hoc bureaucracy (eg. Harberger taxes can essentially replace eminent domain), and given that blockchains lack access to trusted human-controlled courts, these kinds of solutions may prove to be be even more ideal for blockchain-based markets than they are for "real life".I will warn that readers are not at all guaranteed to find the book's proposals acceptable; at least the first three have already been highly controversial and they do contravene many people's moral preconceptions about how property should and should work and where money and markets can and can't be used. The authors are no strangers to controversy; Posner has on previous occasions even proven willing to argue against such notions as human rights law. That said, the book does go to considerable lengths to explain why each proposal improves efficiency if it could be done, and offer multiple versions of each proposal in the hopes that there is at least one (even if partial) implementation of each idea that any given reader can find agreeable.What do Posner and Weyl talk about?The book is split into five major sections, each arguing for a particular reform: self-assessed property taxes, quadratic voting, a new kind of immigration program, breaking up big financial conglomerates that currently make banks and other industries act like monopolies even if they appear at first glance to be competitive, and markets for selling personal data. Properly summarizing all five sections and doing them justice would take too long, so I will focus on a deep summary of one specific section, dealing with a new kind of property taxation, to give the reader a feel for the kinds of ideas that the book is about.Harberger taxesSee also: "Property Is Only Another Name for Monopoly", Posner and WeylMarkets and private property are two ideas that are often considered together, and it is difficult in modern discourse to imagine one without (or even with much less of) the other. In the 19th century, however, many economists in Europe were both libertarian and egalitarian, and it was quite common to appreciate markets while maintaining skepticism toward the excesses of private property. A rather interesting example of this is the Bastiat-Proudhon debate from 1849-1850 where the two dispute the legitimacy of charging interest on loans, with one side focusing on the mutual gains from voluntary contracts and the other focusing on their suspicion of the potential for people with capital to get even richer without working, leading to unbalanced capital accumulation.As it turns out, it is absolutely possible to have a system that contains markets but not property rights: at the end of every year, collect every piece of property, and at the start of the next year have the government auction every piece out to the highest bidder. This kind of system is intuitively quite unrealistic and impractical, but it has the benefit that it achieves perfect allocative efficiency: every year, every object goes to the person who can derive the most value from it (ie. the highest bidder). It also gives the government a large amount of revenue that could be used to completely substitute income and sales taxes or fund a basic income.Now you might ask: doesn't the existing property system also achieve allocative efficiency? After all, if I have an apple, and I value it at $2, and you value it at $3, then you could offer me $2.50 and I would accept. However, this fails to take into account imperfect information: how do you know that I value it at $2, and not $2.70? You could offer to buy it for $2.99 so that you can be sure that you'll get it if you really are the one who values the apple more, but then you would be gaining practically nothing from the transaction. And if you ask me to set the price, how do I know that you value it at $3, and not $2.30? And if I set the price to $2.01 to be sure, I would be gaining practically nothing from the transaction. Unfortunately, there is a result known as the Myerson-Satterthwaite Theorem which means that no solution is efficient; that is, any bargaining algorithm in such a situation must at least sometimes lead to inefficiency from mutually beneficial deals falling through.If there are many buyers you have to negotiate with, things get even harder. If a developer (in the real estate sense) is trying to make a large project that requires buying 100 existing properties, and 99 have already agreed, the remaining one has a strong incentive to charge a very high price, much higher than their actual personal valuation of the property, hoping that the developer will have no choice but to pay up. Well, not necessarily no choice. But a very inconvenient and both privately and socially wasteful choice.Re-auctioning everything once a year completely solves this problem of allocative efficiency, but at a very high cost to investment efficiency: there's no point in building a house in the first place if six months later it will get taken away from you and re-sold in an auction. All property taxes have this problem; if building a house costs you $90 and brings you $100 of benefit, but then you have to pay $15 more property tax if you build the house, then you will not build the house and that $10 gain is lost to society.One of the more interesting ideas from the 19th century economists, and specifically Henry George, was a kind of property tax that did not have this problem: the land value tax. The idea is to charge tax on the value of land, but not the improvements to the land; if you own a $100,000 plot of dirt you would have to pay $5,000 per year taxes on it regardless of whether you used the land to build a condominium or simply as a place to walk your pet doge. A doge.Weyl and Posner are not convinced that Georgian land taxes are viable in practice:Consider, for example, the Empire State Building. What is the pure value of the land beneath it? One could try to infer its value by comparing it to the value of adjoining land. But the building itself defines the neighborhood around it; removing the building would almost certainly change the value of its surrounding land. The land and the building, even the neighborhood, are so tied together, it would be hard to figure out a separate value for each of them.Arguably this does not exclude the possibility of a different kind of Georgian-style land tax: a tax based on the average of property values across a sufficiently large area. That would preserve the property that improving a single piece of land would not (greatly) perversely increase the taxes that they have to pay, without having to find a way to distinguish land from improvements in an absolute sense. But in any case, Posner and Weyl move on to their main proposal: self-assessed property taxes.Consider a system where property owners themselves specify what the value of their property is, and pay a tax rate of, say, 2% of that value per year. But here is the twist: whatever value they specify for their property, they have to be willing to sell it to anyone at that price.If the tax rate is equal to the chance per year that the property gets sold, then this achieves optimal allocative efficiency: raising your self-assessed property value by $1 increases the tax you pay by $0.02, but it also means there is a 2% chance that someone will buy the property and pay $1 more, so there is no incentive to cheat in either direction. It does harm investment efficiency, but vastly less so than all property being re-auctioned every year.Posner and Weyl then point out that if more investment efficiency is desired, a hybrid solution with a lower property tax is possible:When the tax is reduced incrementally to improve investment efficiency, the loss in allocative efficiency is less than the gain in investment efficiency. The reason is that the most valuable sales are ones where the buyer is willing to pay significantly more than the seller is willing to accept. These transactions are the first ones enabled by a reduction in the price as even a small price reduction will avoid blocking these most valuable transactions. In fact, it can be shown that the size of the social loss from monopoly power grows quadratically in the extent of this power. Thus, reducing the markup by a third eliminates close to \(\frac = (3^2-2^2)/(3^2\)) of the allocative harm from private ownership.This concept of quadratic deadweight loss is a truly important insight in economics, and is arguably the deep reason why "moderation in all things" is such an attractive principle: the first step you take away from an extreme will generally be the most valuable. The book then proceeds to give a series of side benefits that this tax would have, as well as some downsides. One interesting side benefit is that it removes an information asymmetry flaw that exists with property sales today, where owners have the incentive to expend effort on making their property look good even in potentially misleading ways. With a properly set Harberger tax, if you somehow mange to trick the world into thinking your house is 5% more valuable, you'll get 5% more when you sell it but until that point you'll have to pay 5% more in taxes, or else someone will much more quickly snap it up from you at the original price.The downsides are smaller than they seem; for example, one natural disadvantage is that it exposes property owners to uncertainty due to the possibility that someone will snap up their property at any time, but that is hardly an unknown as it's a risk that renters already face every day. But Weyl and Posner do propose more moderate ways of introducing the tax that don't have these issues. First, the tax can be applied to types of property that are currently government owned; it's a potentially superior alternative to both continued government ownership and traditional full-on privatization. Second, the tax can be applied to forms of property that are already "industrial" in usage: radio spectrum licenses, domain names, intellectual property, etc.The Rest of the BookThe remaining chapters bring up similar ideas that are similar in spirit to the discussion on Harberger taxes in their use of modern game-theoretic principles to make mathematically optimized versions of existing social institutions. One of the proposals is for something called quadratic voting, which I summarize as follows.Suppose that you can vote as many times as you want, but voting costs "voting tokens" (say each citizen is assigned \(N\) voting tokens per year), and it costs tokens in a nonlinear way: your first vote costs one token, your second vote costs two tokens, and so forth. If someone feels more strongly about something, the argument goes, they would be willing to pay more for a single vote; quadratic voting takes advantage of this by perfectly aligning quantity of votes with cost of votes: if you're willing to pay up to 15 tokens for a vote, then you will keep buying votes until your last one costs 15 tokens, and so you will cast 15 votes in total. If you're willing to pay up to 30 tokens for a vote, then you will keep buying votes until you can't buy any more for a price less than or equal to 30 tokens, and so you will end up casting 30 votes. The voting is "quadratic" because the total amount you pay for \(N\) votes goes up proportionately to \(N^2\). After this, the book describes a market for immigration visas that could greatly expand the number of immigrants admitted while making sure local residents benefit and at the same time aligning incentives to encourage visa sponsors to choose immigrants that are more ikely to succeed in the country and less likely to commit crimes, then an enhancement to antitrust law, and finally the idea of setting up markets for personal data.Markets in EverythingThere are plenty of ways that one could respond to each individual proposal made in the book. I personally, for example, find the immigration visa scheme that Posner and Weyl propose well-intentioned and see how it could improve on the status quo, but also overcomplicated, and it seems simpler to me to have a scheme where visas are auctioned or sold every year, with an additional requirement for migrants to obtain liability insurance. Robin Hanson recently proposed greatly expanding liability insurance mandates as an alternative to many kinds of regulation, and while imposing new mandates on an entire society seems unrealistic, a new expanded immigration program seems like the perfect place to start considering them. Paying people for personal data is interesting, but there are concerns about adverse selection: to put it politely, the kinds of people that are willing to sit around submitting lots of data to Facebook all year to earn $16.92 (Facebook's current annualized revenue per user) are not the kinds of people that advertisers are willing to burn hundreds of dollars per person trying to market rolexes and Lambos to. However, what I find more interesting is the general principle that the book tries to promote.Over the last hundred years, there truly has been a large amount of research into designing economic mechanisms that have desirable properties and that outperform simple two-sided buy-and-sell markets. Some of this research has been put into use in some specific industries; for example, combinatorial auctions are used in airports, radio spectrum auctions and several other industrial use cases, but it hasn't really seeped into any kind of broader policy design; the political systems and property rights that we have are still largely the same as we had two centuries ago. So can we use modern economic insights to reform base-layer markets and politics in such a deep way, and if so, should we?Normally, I love markets and clean incentive alignment, and dislike politics and bureaucrats and ugly hacks, and I love economics, and I so love the idea of using economic insights to design markets that work better so that we can reduce the role of politics and bureaucrats and ugly hacks in society. Hence, naturally, I love this vision. So let me be a good intellectual citizen and do my best to try to make a case against it.There is a limit to how complex economic incentive structures and markets can be because there is a limit to users' ability to think and re-evaluate and give ongoing precise measurements for their valuations of things, and people value reliability and certainty. Quoting Steve Waldman criticizing Uber surge pricing:Finally, we need to consider questions of economic calculation. In macroeconomics, we sometimes face tradeoffs between an increasing and unpredictably variable price-level and full employment. Wisely or not, our current policy is to stabilize the price level, even at short-term cost to output and employment, because stable prices enable longer-term economic calculation. That vague good, not visible on a supply/demand diagram, is deemed worth very large sacrifices. The same concern exists in a microeconomic context. If the "ride-sharing revolution" really takes hold, a lot of us will have decisions to make about whether to own a car or rely upon the Sidecars, Lyfts, and Ubers of the world to take us to work every day. To make those calculations, we will need something like predictable pricing. Commuting to our minimum wage jobs (average is over!) by Uber may be OK at standard pricing, but not so OK on a surge. In the desperate utopia of the "free-market economist", there is always a solution to this problem. We can define futures markets on Uber trips, and so hedge our exposure to price volatility! In practice that is not so likely...And:It's clear that in a lot of contexts, people have a strong preference for price-predictability over immediate access. The vast majority of services that we purchase and consume are not price-rationed in any fine-grained way. If your hairdresser or auto mechanic is busy, you get penciled in for next week...Strong property rights are valuable for the same reason: beyond the arguments about allocative and investment efficiency, they provide the mental convenience and planning benefits of predictability.It's worth noting that even Uber itself doesn't do surge pricing in the "market-based" way that economists would recommend. Uber is not a market where drivers can set their own prices, riders can see what prices are available, and themselves choose their tradeoff between price and waiting time. Why does Uber not do this? One argument is that, as Steve Waldman says, "Uber itself is a cartel", and wants to have the power to adjust market prices not just for efficiency but also reasons such as profit maximization, strategically setting prices to drive out competing platforms (and taxis and public transit), and public relations. As Waldman further points out, one Uber competitor, Sidecar, does have the ability for drivers to set prices, and I would add that I have seen ride-sharing apps in China where passengers can offer drivers higher prices to try to coax them to get a car faster.A possible counter-argument that Uber might give is that drivers themselves are actually less good at setting optimal prices than Uber's own algorithms, and in general people value the convenience of one-click interfaces over the mental complexity of thinking about prices. If we assume that Uber won its market dominance over competitors like Sidecar fairly, then the market itself has decided that the economic gain from marketizing more things is not worth the mental transaction costs.Harberger taxes, at least to me, seem like they would lead to these exact kinds of issues multipled by ten; people are not experts at property valuation, and would have to spend a significant amount of time and mental effort figuring out what self-assessed value to put for their house, and they would complain much more if they accidentally put a value that's too low and suddenly find that their house is gone. If Harberger taxes were to be applied to smaller property items as well, people would need to juggle a large amount of mental valuations of everything. A similar critique could apply to many kinds of personal data markets, and possibly even to quadratic voting if implemented in its full form.I could challenge this by saying "ah, even if that's true, this is the 21st century, we could have companies that build AIs that make pricing decisions on your behalf, and people could choose the AI that seems to work best; there could even be a public option"; and Posner and Weyl themselves suggest that this is likely the way to go. And this is where the interesting conversation starts.Tales from Crypto LandOne reason why this discussion particularly interests me is that the cryptocurrency and blockchain space itself has, in some cases, run up against similar challenges. In the case of Harberger taxes, we actually did consider almost exactly that same proposal in the context of the Ethereum Name System (our decentralized alternative to DNS), but the proposal was ultimately rejected. I asked the ENS developers why it was rejected. Paraphrasing their reply, the challenge is as follows.Many ENS domain names are of a type that would only be interesting to precisely two classes of actors: (i) the "legitimate owner" of some given name, and (ii) scammers. Furthermore, in some particular cases, the legitimate owner is uniquely underfunded, and scammers are uniquely dangerous. One particular case is MyEtherWallet, an Ethereum wallet provider. MyEtherWallet provides an important public good to the Ethereum ecosystem, making Ethereum easier to use for many thousands of people, but is able to capture only a very small portion of the value that it provides; as a result, the budget that it has for outbidding others for the domain name is low. If a scammer gets their hands on the domain, users trusting MyEtherWallet could easily be tricked into sending all of their ether (or other Ethereum assets) to a scammer. Hence, because there is generally one clear "legitimate owner" for any domain name, a pure property rights regime presents little allocative efficiency loss, and there is a strong overriding public interest toward stability of reference (ie. a domain that's legitimate one day doesn't redirect to a scam the next day), so any level of Harberger taxation may well bring more harm than good.I suggested to the ENS developers the idea of applying Harberger taxes to short domains (eg. abc.eth), but not long ones; the reply was that it would be too complicated to have two classes of names. That said, perhaps there is some version of the proposal that could satisfy the specific constraints here; I would be interested to hear Posner and Weyl's feedback on this particular application.Another story from the blockchain and Ethereum space that has a more pro-radical-market conclusion is that of transaction fees. The notion of mental transaction costs, the idea that the inconvenience of even thinking about whether or not some small payment for a given digital good is worth it is enough of a burden to prevent "micro-markets" from working, is often used as an argument for why mass adoption of blockchain tech would be difficult: every transaction requires a small fee, and the mental expenditure of figuring out what fee to pay is itself a major usability barrier. These arguments increased further at the end of last year, when both Bitcoin and Ethereum transaction fees briefly spiked up by a factor of over 100 due to high usage (talk about surge pricing!), and those who accidentally did not pay high enough fees saw their transactions get stuck for days.That said, this is a problem that we have now, arguably, to a large extent overcome. After the spikes at the end of last year, Ethereum wallets developed more advanced algorithms for choosing what transaction fees to pay to ensure that one's transaction gets included in the chain, and today most users are happy to simply defer to them. In my own personal experience, the mental transaction costs of worrying about transaction fees do not really exist, much like a driver of a car does not worry about the gasoline consumed by every single turn, acceleration and braking made by their car. Personal price-setting AIs for interacting with open markets: already a reality in the Ethereum transaction fee marketA third kind of "radical market" that we are considering implementing in the context of Ethereum's consensus system is one for incentivizing deconcentration of validator nodes in proof of stake consensus. It's important for blockchains to be decentralized, a similar challenge to what antitrust law tries to solve, but the tools at our disposal are different. Posner and Weyl's solution to antitrust, banning institutional investment funds from owning shares in multiple competitors in the same industry, is far too subjective and human-judgement-dependent to work in a blockchain, but for our specific context we have a different solution: if a validator node commits an error, it gets penalized an amount proportional to the number of other nodes that have committed an error around the same time. This incentivizes nodes to set themselves up in such a way that their failure rate is maximally uncorrelated with everyone else's failure rate, reducing the chance that many nodes fail at the same time and threaten to the blockchain's integrity. I want to ask Posner and Weyl: though our exact approach is fairly application-specific, could a similarly elegant "market-based" solution be discovered to incentivize market deconcentration in general?All in all, I am optimistic that the various behavioral kinks around implementing "radical markets" in practice could be worked out with the help of good defaults and personal AIs, though I do think that if this vision is to be pushed forward, the greatest challenge will be finding progressively larger and more meaningful places to test it out and show that the model works. I particularly welcome the use of the blockchain and crypto space as a testing ground.Another Kind of Radical MarketThe book as a whole tends to focus on centralized reforms that could be implemented on an economy from the top down, even if their intended long-term effect is to push more decision-making power to individuals. The proposals involve large-scale restructurings of how property rights work, how voting works, how immigration and antitrust law works, and how individuals see their relationship with property, money, prices and society. But there is also the potential to use economics and game theory to come up with decentralized economic institutions that could be adopted by smaller groups of people at a time.Perhaps the most famous examples of decentralized institutions from game theory and economics land are (i) assurance contracts, and (ii) prediction markets. An assurance contract is a system where some public good is funded by giving anyone the opportunity to pledge money, and only collecting the pledges if the total amount pledged exceeds some threshold. This ensures that people can donate money knowing that either they will get their money back or there actually will be enough to achieve some objective. A possible extension of this concept is Alex Tabarrok's dominant assurance contracts, where an entrepreneur offers to refund participants more than 100% of their deposits if a given assurance contract does not raise enough money.Prediction markets allow people to bet on the probability that events will happen, potentially even conditional on some action being taken ("I bet $20 that unemployment will go down if candidate X wins the election"); there are techniques for people interested in the information to subsidize the markets. Any attempt to manipulate the probability that a prediction market shows simply creates an opportunity for people to earn free money (yes I know, risk aversion and capital efficiency etc etc; still close to free) by betting against the manipulator.Posner and Weyl do give one example of what I would call a decentralized institution: a game for choosing who gets an asset in the event of a divorce or a company splitting in half, where both sides provide their own valuation, the person with the higher valuation gets the item, but they must then give an amount equal to half the average of the two valuations to the loser. There's some economic reasoning by which this solution, while not perfect, is still close to mathematically optimal.One particular category of decentralized institutions I've been interested in is improving incentivization for content posting and content curation in social media. Some ideas that I have had include:Proof of stake conditional hashcash (when you send someone an email, you give them the opportunity to burn $0.5 of your money if they think it's spam) Prediction markets for content curation (use prediction markets to predict the results of a moderation vote on content, thereby encouraging a market of fast content pre-moderators while penalizing manipulative pre-moderation) Conditional payments for paywalled content (after you pay for a piece of downloadable content and view it, you can decide after the fact if payments should go to the author or to proportionately refund previous readers) And ideas I have had in other contexts:Call-out assurance contracts DAICOs (a more decentralized and safer alternative to ICOs) Twitter scammers: can prediction markets incentivize an autonomous swarm of human and AI-driven moderators to flag these posts and warn users not to send them ether within a few seconds of the post being made? And could such a system be generalized to the entire internet, where these is no single centralized moderator that can easily take posts down?Some ideas others have had for decentralized institutions in general include:TrustDavis (adding skin-in-the-game to e-commerce reputations by making e-commerce ratings be offers to insure others against the receiver of the rating committing fraud) Circles (decentralized basic income through locally fungible coin issuance) Markets for CAPTCHA services Digitized peer to peer rotating savings and credit associations Token curated registries Crowdsourced smart contract truth oracles Using blockchain-based smart contracts to coordinate unions I would be interested in hearing Posner and Weyl's opinion on these kinds of "radical markets", that groups of people can spin up and start using by themselves without requiring potentially contentious society-wide changes to political and property rights. Could decentralized institutions like these be used to solve the key defining challenges of the twenty first century: promoting beneficial scientific progress, developing informational public goods, reducing global wealth inequality, and the big meta-problem behind fake news, government-driven and corporate-driven social media censorship, and regulation of cryptocurrency products: how do we do quality assurance in an open society?All in all, I highly recommend Radical Markets (and by the way I also recommend Eliezer Yudkowsky's Inadequate Equilibria) to anyone interested in these kinds of issues, and look forward to seeing the discussion that the book generates.

Governance, Part 2: Plutocracy Is Still Bad Governance, Part 2: Plutocracy Is Still Bad2018 Mar 28 See all posts Governance, Part 2: Plutocracy Is Still Bad Coin holder voting, both for governance of technical features, and for more extensive use cases like deciding who runs validator nodes and who receives money from development bounty funds, is unfortunately continuing to be popular, and so it seems worthwhile for me to write another post explaining why I (and Vlad Zamfir and others) do not consider it wise for Ethereum (or really, any base-layer blockchain) to start adopting these kinds of mechanisms in a tightly coupled form in any significant way.I wrote about the issues with tightly coupled voting in a blog post last year, that focused on theoretical issues as well as focusing on some practical issues experienced by voting systems over the previous two years. Now, the latest scandal in DPOS land seems to be substantially worse. Because the delegate rewards in EOS are now so high (5% annual inflation, about $400m per year), the competition on who gets to run nodes has essentially become yet another frontier of US-China geopolitical economic warfare. And that's not my own interpretation; I quote from this article (original in Chinese):EOS supernode voting: multibillion-dollar profits leading to crypto community inter-country warfareLooking at community recognition, Chinese nodes feel much less represented in the community than US and Korea. Since the EOS.IO official Twitter account was founded, there has never been any interaction with the mainland Chinese EOS community. For a listing of the EOS officially promoted events and interactions with communities see the picture below. With no support from the developer community, facing competition from Korea, the Chinese EOS supernodes have invented a new strategy: buying votes.The article then continues to describe further strategies, like forming "alliances" that all vote (or buy votes) for each other.Of course, it does not matter at all who the specific actors are that are buying votes or forming cartels; this time it's some Chinese pools, last time it was "members located in the USA, Russia, India, Germany, Canada, Italy, Portugal and many other countries from around the globe", next time it could be totally anonymous, or run out of a smartphone snuck into Trendon Shavers's prison cell. What matters is that blockchains and cryptocurrency, originally founded in a vision of using technology to escape from the failures of human politics, have essentially all but replicated it. Crypto is a reflection of the world at large.The EOS New York community's response seems to be that they have issued a strongly worded letter to the world stating that buying votes will be against the constitution. Hmm, what other major political entity has made accepting bribes a violation of the constitution? And how has that been going for them lately?The second part of this article will involve me, an armchair economist, hopefully convincing you, the reader, that yes, bribery is, in fact, bad. There are actually people who dispute this claim; the usual argument has something to do with market efficiency, as in "isn't this good, because it means that the nodes that win will be the nodes that can be the cheapest, taking the least money for themselves and their expenses and giving the rest back to the community?" The answer is, kinda yes, but in a way that's centralizing and vulnerable to rent-seeking cartels and explicitly contradicts many of the explicit promises made by most DPOS proponents along the way.Let us create a toy economic model as follows. There are a number of people all of which are running to be delegates. The delegate slot gives a reward of $100 per period, and candidates promise to share some portion of that as a bribe, equally split among all of their voters. The actual \(N\) delegates (eg. \(N = 35\)) in any period are the \(N\) delegates that received the most votes; that is, during every period a threshold of votes emerges where if you get more votes than that threshold you are a delegate, if you get less you are not, and the threshold is set so that \(N\) delegates are above the threshold.We expect that voters vote for the candidate that gives them the highest expected bribe. Suppose that all candidates start off by sharing 1%; that is, equally splitting $1 among all of their voters. Then, if some candidate becomes a delegate with \(K\) voters, each voter gets a payment of \(\frac\). The candidate that it's most profitable to vote for is a candidate that's expected to be in the top \(N\), but is expected to earn the fewest votes within that set. Thus, we expect votes to be fairly evenly split among 35 delegates.Now, some candidates will want to secure their position by sharing more; by sharing 2%, you are likely to get twice as many votes as those that share 1%, as that's the equilibrium point where voting for you has the same payout as voting for anyone else. The extra guarantee of being elected that this gives is definitely worth losing an additional 1% of your revenue when you do get elected. We can expect delegates to bid up their bribes and eventually share something close to 100% of their revenue. So the outcome seems to be that the delegate payouts are largely simply returned to voters, making the delegate payout mechanism close to meaningless.But it gets worse. At this point, there's an incentive for delegates to form alliances (aka political parties, aka cartels) to coordinate their share percentages; this reduces losses to the cartel from chaotic competition that accidentally leads to some delegates not getting enough votes. Once a cartel is in place, it can start bringing its share percentages down, as dislodging it is a hard coordination problem: if a cartel offers 80%, then a new entrant offers 90%, then to a voter, seeking a share of that extra 10% is not worth the risk of either (i) voting for someone who gets insufficient votes and does not pay rewards, or (ii) voting for someone who gets too many votes and so pays out a reward that's excessively diluted. Sidenote: Bitshares DPOS used approval voting, where you can vote for as many candidates as you want; it should be pretty obvious that with even slight bribery, the equilibrium there is that everyone just votes for everyone.Furthermore, even if cartel mechanics don't come into play, there is a further issue. This equilibrium of coin holders voting for whoever gives them the most bribes, or a cartel that has become an entrenched rent seeker, contradicts explicit promises made by DPOS proponents.Quoting "Explain Delegated Proof of Stake Like I'm 5":If a Witness starts acting like an asshole, or stops doing a quality job securing the network, people in the community can remove their votes, essentially firing the bad actor. Voting is always ongoing.From "EOS: An Introduction":By custom, we suggest that the bulk of the value be returned to the community for the common good - software improvements, dispute resolution, and the like can be entertained. In the spirit of "eating our own dogfood," the design envisages that the community votes on a set of open entry contracts that act like "foundations" for the benefit of the community. Known as Community Benefit Contracts, the mechanism highlights the importance of DPOS as enabling direct on-chain governance by the community (below).The flaw in all of this, of course, is that the average voter has only a very small chance of impacting which delegates get selected, and so they only have a very small incentive to vote based on any of these high-minded and lofty goals; rather, their incentive is to vote for whoever offers the highest and most reliable bribe. Attacking is easy. If a cartel equilibrium does not form, then an attacker can simply offer a share percentage slightly higher than 100% (perhaps using fee sharing or some kind of "starter promotion" as justification), capture the majority of delegate positions, and then start an attack. If they get removed from the delegate position via a hard fork, they can simply restart the attack again with a different identity.The above is not intended purely as a criticism of DPOS consensus or its use in any specific blockchain. Rather, the critique reaches much further. There has been a large number of projects recently that extol the virtues of extensive on-chain governance, where on-chain coin holder voting can be used not just to vote on protocol features, but also to control a bounty fund. Quoting a blog post from last year:Anyone can submit a change to the governance structure in the form of a code update. An on-chain vote occurs, and if passed, the update makes its way on to a test network. After a period of time on the test network, a confirmation vote occurs, at which point the change goes live on the main network. They call this concept a "self-amending ledger". Such a system is interesting because it shifts power towards users and away from the more centralized group of developers and miners. On the developer side, anyone can submit a change, and most importantly, everyone has an economic incentive to do it. Contributions are rewarded by the community with newly minted tokens through inflation funding. This shifts from the current Bitcoin and Ethereum dynamics where a new developer has little incentive to evolve the protocol, thus power tends to concentrate amongst the existing developers, to one where everyone has equal earning power.In practice, of course, what this can easily lead to is funds that offer kickbacks to users who vote for them, leading to the exact scenario that we saw above with DPOS delegates. In the best case, the funds will simply be returned to voters, giving coin holders an interest rate that cancels out the inflation, and in the worst case, some portion of the inflation will get captured as economic rent by a cartel.Note also that the above is not a criticism of all on-chain voting; it does not rule out systems like futarchy. However, futarchy is untested, but coin voting is tested, and so far it seems to lead to a high risk of economic or political failure of some kind - far too high a risk for a platform that seeks to be an economic base layer for development of decentralized applications and institutions.So what's the alternative? The answer is what we've been saying all along: cryptoeconomics. Cryptoeconomics is fundamentally about the use of economic incentives together with cryptography to design and secure different kinds of systems and applications, including consensus protocols. The goal is simple: to be able to measure the security of a system (that is, the cost of breaking the system or causing it to violate certain guarantees) in dollars. Traditionally, the security of systems often depends on social trust assumptions: the system works if 2 of 3 of Alice, Bob and Charlie are honest, and we trust Alice, Bob and Charlie to be honest because I know Alice and she's a nice girl, Bob registered with FINCEN and has a money transmitter license, and Charlie has run a successful business for three years and wears a suit.Social trust assumptions can work well in many contexts, but they are difficult to universalize; what is trusted in one country or one company or one political tribe may not be trusted in others. They are also difficult to quantify; how much money does it take to manipulate social media to favor some particular delegate in a vote? Social trust assumptions seem secure and controllable, in the sense that "people" are in charge, but in reality they can be manipulated by economic incentives in all sorts of ways.Cryptoeconomics is about trying to reduce social trust assumptions by creating systems where we introduce explicit economic incentives for good behavior and economic penalties for bad behavior, and making mathematical proofs of the form "in order for guarantee \(X\) to be violated, at least these people need to misbehave in this way, which means the minimum amount of penalties or foregone revenue that the participants suffer is \(Y\)". Casper is designed to accomplish precisely this objective in the context of proof of stake consensus. Yes, this does mean that you can't create a "blockchain" by concentrating the consensus validation into 20 uber-powerful "supernodes" and you have to actually think to make a design that intelligently breaks through and navigates existing tradeoffs and achieves massive scalability in a still-decentralized network. But the reward is that you don't get a network that's constantly liable to breaking in half or becoming economically captured by unpredictable political forces.It has been brought to my attention that EOS may be reducing its delegate rewards from 5% per year to 1% per year. Needless to say, this doesn't really change the fundamental validity of any of the arguments; the only result of this would be 5x less rent extraction potential at the cost of a 5x reduction to the cost of attacking the system. Some have asked: but how can it be wrong for DPOS delegates to bribe voters, when it is perfectly legitimate for mining and stake pools to give 99% of their revenues back to their participants? The answer should be clear: in PoW and PoS, it's the protocol's role to determine the rewards that miners and validators get, based on the miners and validators' observed performance, and the fact that miners and validators that are pools pass along the rewards (and penalties!) to their participants gives the participants an incentive to participate in good pools. In DPOS, the reward is constant, and it's the voters' role to vote for pools that have good performance, but with the key flaw that there is no mechanism to actually encourage voters to vote in that way instead of just voting for whoever gives them the most money without taking performance into account. Penalties in DPOS do not exist, and are certainly not passed on to voters, so voters have no "skin in the game" (penalties in Casper pools, on the other hand, do get passed on to participants).

Proof of Stake FAQ Proof of Stake FAQ2017 Dec 31 See all posts Proof of Stake FAQ ContentsWhat is Proof of Stake What are the benefits of proof of stake as opposed to proof of work? How does proof of stake fit into traditional Byzantine fault tolerance research? What is the "nothing at stake" problem and how can it be fixed? That shows how chain-based algorithms solve nothing-at-stake. Now how do BFT-style proof of stake algorithms work? What is "economic finality" in general? So how does this relate to Byzantine fault tolerance theory? What is "weak subjectivity"? Can we try to automate the social authentication to reduce the load on users? Can one economically penalize censorship in proof of stake? How does validator selection work, and what is stake grinding? What would the equivalent of a 51% attack against Casper look like? That sounds like a lot of reliance on out-of-band social coordination; is that not dangerous? Doesn't MC

Sharding FAQ Sharding FAQ2017 Dec 31 See all posts Sharding FAQ Currently, in all blockchain protocols each node stores the entire state (account balances, contract code and storage, etc.) and processes all transactions. This provides a large amount of security, but greatly limits scalability: a blockchain cannot process more transactions than a single node can. In large part because of this, Bitcoin is limited to ~3–7 transactions per second, Ethereum to 7–15, etc.However, this poses a question: are there ways to create a new mechanism, where only a small subset of nodes verifies each transaction? As long as there are sufficiently many nodes verifying each transaction that the system is still highly secure, but a sufficiently small percentage of the total validator set so that the system can process many transactions in parallel, could we not split up transaction processing between smaller groups of nodes to greatly increase a blockchain's total throughput? ContentsWhat are some trivial but flawed ways of solving the problem? This sounds like there's some kind of scalability trilemma at play. What is this trilemma and can we break through it? What are some moderately simple but only partial ways of solving the scalability problem? What about approaches that do not try to "shard" anything? How does Plasma, state channels and other layer 2 technologies fit into the trilemma? State size, history, cryptoeconomics, oh my! Define some of these terms before we move further! What is the basic idea behind sharding? What might a basic design of a sharded blockchain look like? What are the challenges here? But doesn't the CAP theorem mean that fully secure distributed systems are impossible, and so sharding is futile? What are the security models that we are operating under? How can we solve the single-shard takeover attack in an uncoordinated majority model? How do you actually do this sampling in proof of work, and in proof of stake? How is the randomness for random sampling generated? What are the tradeoffs in making sampling more or less frequent? Can we force more of the state to be held user-side so that transactions can be validated without requiring validators to hold all state data? Can we split data and execution so that we get the security from rapid shuffling data validation without the overhead of shuffling the nodes that perform state execution? Can SNARKs and STARKs help? How can we facilitate cross-shard communication? What is the train-and-hotel problem? What are the concerns about sharding through random sampling in a bribing attacker or coordinated choice model? How can we improve on this? What is the data availability problem, and how can we use erasure codes to solve it? Can we remove the need to solve data availability with some kind of fancy cryptographic accumulator scheme? So this means that we can actually create scalable sharded blockchains where the cost of making anything bad happen is proportional to the size of the entire validator set? Let's walk back a bit. Do we actually need any of this complexity if we have instant shuffling? Doesn't instant shuffling basically mean that each shard directly pulls validators from the global validator pool so it operates just like a blockchain, and so sharding doesn't actually introduce any new complexities? You mentioned transparent sharding. I'm 12 years old and what is this? What are some advantages and disadvantages of this? How would synchronous cross-shard messages work? What about semi-asynchronous messages? What are guaranteed cross-shard calls? Wait, but what if an attacker sends a cross-shard call from every shard into shard X at the same time? Wouldn't it be mathematically impossible to include all of these calls in time? Congealed gas? This sounds interesting for not just cross-shard operations, but also reliable intra-shard scheduling Does guaranteed scheduling, both intra-shard and cross-shard, help against majority collusions trying to censor transactions? Could sharded blockchains do a better job of dealing with network partitions? What are the unique challenges of pushing scaling past n = O(c^2)? What about heterogeneous sharding? Footnotes What are some trivial but flawed ways of solving the problem?There are three main categories of "easy solutions". The first is to give up on scaling individual blockchains, and instead assume that applications will be split among many different chains. This greatly increases throughput, but at a cost of security: an N-factor increase in throughput using this method necessarily comes with an N-factor decrease in security, as a level of resources 1/N the size of the whole ecosystem will be sufficient to attack any individual chain. Hence, it is arguably non-viable for more than small values of N.The second is to simply increase the block size limit. This can work and in some situations may well be the correct prescription, as block sizes may well be constrained more by politics than by realistic technical considerations. But regardless of one's beliefs about any individual case such an approach inevitably has its limits: if one goes too far, then nodes running on consumer hardware will drop out, the network will start to rely exclusively on a very small number of supercomputers running the blockchain, which can lead to great centralization risk.The third is "merge mining", a technique where there are many chains, but all chains share the same mining power (or, in proof of stake systems, stake). Currently, Namecoin gets a large portion of its security from the Bitcoin blockchain by doing this. If all miners participate, this theoretically can increase throughput by a factor of N without compromising security. However, this also has the problem that it increases the computational and storage load on each miner by a factor of N, and so in fact this solution is simply a stealthy form of block size increase.This sounds like there's some kind of scalability trilemma at play. What is this trilemma and can we break through it?The trilemma claims that blockchain systems can only at most have two of the following three properties:Decentralization (defined as the system being able to run in a scenario where each participant only has access to O(c) resources, i.e. a regular laptop or small VPS) Scalability (defined as being able to process O(n) > O(c) transactions) Security (defined as being secure against attackers with up to O(n) resources) In the rest of this document, we'll continue using c to refer to the size of computational resources (including computation, bandwidth and storage) available to each node, and n to refer to the size of the ecosystem in some abstract sense; we assume that transaction load, state size, and the market cap of a cryptocurrency are all proportional to n. The key challenge of scalability is finding a way to achieve all three at the base layer.What are some moderately simple but only partial ways of solving the scalability problem?Many sharding proposals (e.g. this early BFT sharding proposal from Loi Luu et al at NUS, more recent application of similar ideas in Zilliqa, as well as this Merklix tree1 approach that has been suggested for Bitcoin) attempt to either only shard transaction processing or only shard state, without touching the other2. These efforts can lead to some gains in efficiency, but they run into the fundamental problem that they only solve one of the two bottlenecks. We want to be able to process 10,000+ transactions per second without either forcing every node to be a supercomputer or forcing every node to store a terabyte of state data, and this requires a comprehensive solution where the workloads of state storage, transaction processing and even transaction downloading and re-broadcasting at are all spread out across nodes. Particularly, the P2P network needs to also be modified to ensure that not every node receives all information from every other node.What about approaches that do not try to "shard" anything?Bitcoin-NG can increase scalability somewhat by means of an alternative blockchain design that makes it much safer for the network if nodes are spending large portions of their CPU time verifying blocks. In simple PoW blockchains, there are high centralization risks and the safety of consensus is weakened if capacity is increased to the point where more than about 5% of nodes' CPU time is spent verifying blocks; Bitcoin-NG's design alleviates this problem. However, this can only increase the scalability of transaction capacity by a constant factor of perhaps 5-50x3,4, and does not increase the scalability of state. That said, Bitcoin-NG-style approaches are not mutually exclusive with sharding, and the two can certainly be implemented at the same time.Channel-based strategies (lightning network, Raiden, etc) can scale transaction capacity by a constant factor but cannot scale state storage, and also come with their own unique sets of tradeoffs and limitations particularly involving denial-of-service attacks. On-chain scaling via sharding (plus other techniques) and off-chain scaling via channels are arguably both necessary and complementary.There exist approaches that use advanced cryptography, such as Mimblewimble and strategies based on ZK-SNARKs (eg. Coda), to solve one specific part of the scaling problem: initial full node synchronization. Instead of verifying the entire history from genesis, nodes could verify a cryptographic proof that the current state legitimately follows from the history. These approaches do solve a legitimate problem, but they are not a substitute for sharding, as they do not remove the need for nodes to download and verify very large amounts of data to stay on the chain in real time.How does Plasma, state channels and other layer 2 technologies fit into the trilemma?In the event of a large attack on Plasma subchains, all users of the Plasma subchains would need to withdraw back to the root chain. If Plasma has O(N) users, then this will require O(N) transactions, and so O(N / C) time to process all of the withdrawals. If withdrawal delays are fixed to some D (i.e. the naive implementation), then as soon as N > C * D, there will not be enough space in the blockchain to process all withdrawals in time, and so the system will be insecure; in this mode, Plasma should be viewed as increasing scalability only by a (possibly large) constant factor. If withdrawal delays are flexible, so they automatically extend if there are many withdrawals being made, then this means that as N increases further and further, the amount of time that an attacker can force everyone's funds to get locked up increases, and so the level of "security" of the system decreases further and further in a certain sense, as extended denial of access can be viewed as a security failure, albeit one milder than total loss of access. However, this is a different direction of tradeoff from other solutions, and arguably a much milder tradeoff, hence why Plasma subchains are nevertheless a large improvement on the status quo.Note that there is one design that states that: "Given a malicious operator (the worst case), the system degrades to an on-chain token. A malicious operator cannot steal funds and cannot deprive people of their funds for any meaningful amount of time."—https://ethresear.ch/t/roll-up-roll-back-snark-side-chain-17000-tps/3675. See also here for related information.State channels have similar properties, though with different tradeoffs between versatility and speed of finality. Other layer 2 technologies include TrueBit off-chain interactive verification of execution and Raiden, which is another organisation working on state channels. Proof of stake with Casper (which is layer 1) would also improve scaling—it is more decentralizable, not requiring a computer that is able to mine, which tends towards centralized mining farms and institutionalized mining pools as difficulty increases and the size of the state of the blockchain increases.Sharding is different to state channels and Plasma in that periodically notaries are pseudo-randomly assigned to vote on the validity of collations (analogous to blocks, but without an EVM state transition function in phase 1), then these collations are accepted into the main chain after the votes are verified by a committee on the main chain, via a sharding manager contract on the main chain. In phase 5 (see the roadmap for details), shards are tightly coupled to the main chain, so that if any shard or the main chain is invalid, the whole network is invalid. There are other differences between each mechanism, but at a high level, Plasma, state channels and Truebit are off-chain for an indefinite interval, connect to the main chain at the smart contract, layer 2 level, while they can draw back into and open up from the main chain, whereas shards are regularly linked to the main chain via consensus in-protocol.See also these tweets from Vlad.State size, history, cryptoeconomics, oh my! Define some of these terms before we move further!State: a set of information that represents the "current state" of a system; determining whether or not a transaction is valid, as well as the effect of a transaction, should in the simplest model depend only on state. Examples of state data include the UTXO set in bitcoin, balances + nonces + code + storage in ethereum, and domain name registry entries in Namecoin. History: an ordered list of all transactions that have taken place since genesis. In a simple model, the present state should be a deterministic function of the genesis state and the history. Transaction: an object that goes into the history. In practice, a transaction represents an operation that some user wants to make, and is cryptographically signed. In some systems transactions are called blobs, to emphasize the fact that in these systems these objects may contain arbitrary data and may not in all cases represent an attempt to perform some operation in the protocol. State transition function: a function that takes a state, applies a transaction and outputs a new state. The computation involved may involve adding and subtracting balances from accounts specified by the transaction, verifying digital signatures and running contract code. Merkle tree: a cryptographic hash tree structure that can store a very large amount of data, where authenticating each individual piece of data only takes O(log(n)) space and time. See here for details. In Ethereum, the transaction set of each block, as well as the state, is kept in a Merkle tree, where the roots of the trees are committed to in a block. Receipt: an object that represents an effect of a transaction that is not directly stored in the state, but which is still stored in a Merkle tree and committed to in a block header or in a special location in the state so that its existence can later be efficiently proven even to a node that does not have all of the data. Logs in Ethereum are receipts; in sharded models, receipts are used to facilitate asynchronous cross-shard communication. Light client: a way of interacting with a blockchain that only requires a very small amount (we'll say O(1), though O(log(c)) may also be accurate in some cases) of computational resources, keeping track of only the block headers of the chain by default and acquiring any needed information about transactions, state or receipts by asking for and verifying Merkle proofs of the relevant data on an as-needed basis. State root: the root hash of the Merkle tree representing the state5 The Ethereum 1.0 state tree, and how the state root fits into the block structure What is the basic idea behind sharding?We split the state and history up into K = O(n / c) partitions that we call "shards". For example, a sharding scheme on Ethereum might put all addresses starting with 0x00 into one shard, all addresses starting with 0x01 into another shard, etc. In the simplest form of sharding, each shard also has its own transaction history, and the effect of transactions in some shard k are limited to the state of shard k. One simple example would be a multi-asset blockchain, where there are K shards and each shard stores the balances and processes the transactions associated with one particular asset. In more advanced forms of sharding, some form of cross-shard communication capability, where transactions on one shard can trigger events on other shards, is also included.What might a basic design of a sharded blockchain look like?A simple approach is as follows. For simplicity, this design keeps track of data blobs only; it does not attempt to process a state transition function.There exists a set of validators (ie. proof of stake nodes), who randomly get assigned the right to create shard blocks. During each slot (eg. an 8-second period of time), for each k in [0...999] a random validator gets selected, and given the right to create a block on "shard k", which might contain up to, say, 32 kb of data. Also, for each k, a set of 100 validators get selected as attesters. The header of a block together with at least 67 of the attesting signatures can be published as an object that gets included in the "main chain" (also called a beacon chain).Note that there are now several "levels" of nodes that can exist in such a system:Super-full node - downloads the full data of the beacon chain and every shard block referenced in the beacon chain. Top-level node - processes the beacon chain blocks only, including the headers and signatures of the shard blocks, but does not download all the data of the shard blocks. Single-shard node - acts as a top-level node, but also fully downloads and verifies every collation on some specific shard that it cares more about. Light node - downloads and verifies the block headers of main chain blocks only; does not process any collation headers or transactions unless it needs to read some specific entry in the state of some specific shard, in which case it downloads the Merkle branch to the most recent collation header for that shard and from there downloads the Merkle proof of the desired value in the state. What are the challenges here?Single-shard takeover attacks - what if an attacker takes over the majority of the validators responsible for attesting to one particular block, either to (respectively) prevent any collations from getting enough signatures or, worse, to submit collations that are invalid? State transition execution - single-shard takeover attacks are typically prevented with random sampling schemes, but such schemes also make it more difficult for validators to compute state roots, as they cannot have up-to-date state information for every shard that they could be assigned to. How do we ensure that light clients can still get accurate information about the state? Fraud detection - if an invalid collation or state claim does get made, how can nodes (including light nodes) be reliably informed of this so that they can detect the fraud and reject the collation if it is truly fraudulent? Cross shard communication - the above design supports no cross-shard communication. How do we add cross-shard communication safely? The data availability problem - as a subset of fraud detection, what about the specific case where data is missing from a collation? Superquadratic sharding - in the special case where n > c^2, in the simple design given above there would be more than O(c) collation headers, and so an ordinary node would not be able to process even just the top-level blocks. Hence, more than two levels of indirection between transactions and top-level block headers are required (i.e. we need "shards of shards"). What is the simplest and best way to do this? However, the effect of a transaction may depend on events that earlier took place in other shards; a canonical example is transfer of money, where money can be moved from shard i to shard j by first creating a "debit" transaction that destroys coins in shard i, and then creating a "credit" transaction that creates coins in shard j, pointing to a receipt created by the debit transaction as proof that the credit is legitimate.But doesn't the CAP theorem mean that fully secure distributed systems are impossible, and so sharding is futile?The CAP theorem is a result that has to do with distributed consensus; a simple statement is: "in the cases that a network partition takes place, you have to choose either consistency or availability, you cannot have both". The intuitive argument is simple: if the network splits in half, and in one half I send a transaction "send my 10 coins to A" and in the other I send a transaction "send my 10 coins to B", then either the system is unavailable, as one or both transactions will not be processed, or it becomes inconsistent, as one half of the network will see the first transaction completed and the other half will see the second transaction completed. Note that the CAP theorem has nothing to do with scalability; it applies to any situation where multiple nodes need to agree on a value, regardless of the amount of data that they are agreeing on. All existing decentralized systems have found some compromise between availability and consistency; sharding does not make anything fundamentally harder in this respect.What are the security models that we are operating under?There are several competing models under which the safety of blockchain designs is evaluated:Honest majority (or honest supermajority): we assume that there is some set of validators and up to 50% (or 33% or 25%) of those validators are controlled by an attacker, and the remaining validators honestly follow the protocol. Honest majority models can have non-adaptive or adaptive adversaries; an adversary is adaptive if they can quickly choose which portion of the validator set to "corrupt", and non-adaptive if they can only make that choice far ahead of time. Note that the honest majority assumption may be higher for notary committees with a 61% honesty assumption. Uncoordinated majority: we assume that all validators are rational in a game-theoretic sense (except the attacker, who is motivated to make the network fail in some way), but no more than some fraction (often between 25% and 50%) are capable of coordinating their actions. Coordinated choice: we assume that most or all validators are controlled by the same actor, or are fully capable of coordinating on the economically optimal choice between themselves. We can talk about the cost to the coalition (or profit to the coalition) of achieving some undesirable outcome. Bribing attacker model: we take the uncoordinated majority model, but instead of making the attacker be one of the participants, the attacker sits outside the protocol, and has the ability to bribe any participants to change their behavior. Attackers are modeled as having a budget, which is the maximum that they are willing to pay, and we can talk about their cost, the amount that they end up paying to disrupt the protocol equilibrium. Bitcoin proof of work with Eyal and Sirer's selfish mining fix is robust up to 50% under the honest majority assumption, and up to ~23.21% under the uncoordinated majority assumption. Schellingcoin is robust up to 50% under the honest majority and uncoordinated majority assumptions, has ε (i.e. slightly more than zero) cost of attack in a coordinated choice model, and has a P + ε budget requirement and ε cost in a bribing attacker model due to P + epsilon attacks.Hybrid models also exist; for example, even in the coordinated choice and bribing attacker models, it is common to make an honest minority assumption that some portion (perhaps 1-15%) of validators will act altruistically regardless of incentives. We can also talk about coalitions consisting of between 50-99% of validators either trying to disrupt the protocol or harm other validators; for example, in proof of work, a 51%-sized coalition can double its revenue by refusing to include blocks from all other miners.The honest majority model is arguably highly unrealistic and has already been empirically disproven - see Bitcoin's SPV mining fork for a practical example. It proves too much: for example, an honest majority model would imply that honest miners are willing to voluntarily burn their own money if doing so punishes attackers in some way. The uncoordinated majority assumption may be realistic; there is also an intermediate model where the majority of nodes is honest but has a budget, so they shut down if they start to lose too much money.The bribing attacker model has in some cases been criticized as being unrealistically adversarial, although its proponents argue that if a protocol is designed with the bribing attacker model in mind then it should be able to massively reduce the cost of consensus, as 51% attacks become an event that could be recovered from. We will evaluate sharding in the context of both uncoordinated majority and bribing attacker models. Bribing attacker models are similar to maximally-adaptive adversary models, except that the adversary has the additional power that it can solicit private information from all nodes; this distinction can be crucial, for example Algorand is secure under adaptive adversary models but not bribing attacker models because of how it relies on private information for random selection.How can we solve the single-shard takeover attack in an uncoordinated majority model?In short, random sampling. Each shard is assigned a certain number of notaries (e.g. 150), and the notaries that approve collations on each shard are taken from the sample for that shard. Samples can be reshuffled either semi-frequently (e.g. once every 12 hours) or maximally frequently (i.e. there is no real independent sampling process, notaries are randomly selected for each shard from a global pool every block).Sampling can be explicit, as in protocols that choose specifically sized "committees" and ask them to vote on the validity and availability of specific collations, or it can be implicit, as in the case of "longest chain" protocols where nodes pseudorandomly assigned to build on specific collations and are expected to "windback verify" at least N ancestors of the collation they are building on.The result is that even though only a few nodes are verifying and creating blocks on each shard at any given time, the level of security is in fact not much lower, in an honest or uncoordinated majority model, than what it would be if every single node was verifying and creating blocks. The reason is simple statistics: if you assume a ~67% honest supermajority on the global set, and if the size of the sample is 150, then with 99.999% probability the honest majority condition will be satisfied on the sample. If you assume a 75% honest supermajority on the global set, then that probability increases to 99.999999998% (see here for calculation details).Hence, at least in the honest / uncoordinated majority setting, we have:Decentralization (each node stores only O(c) data, as it's a light client in O(c) shards and so stores O(1) * O(c) = O(c) data worth of block headers, as well as O(c) data corresponding to the recent history of one or several shards that it is assigned to at the present time) Scalability (with O(c) shards, each shard having O(c) capacity, the maximum capacity is n = O(c^2)) Security (attackers need to control at least ~33% of the entire O(n)-sized validator pool in order to stand a chance of taking over the network). In the bribing attacker model (or in the "very very adaptive adversary" model), things are not so easy, but we will get to this later. Note that because of the imperfections of sampling, the security threshold does decrease from 50% to ~30-40%, but this is still a surprisingly low loss of security for what may be a 100-1000x gain in scalability with no loss of decentralization.How do you actually do this sampling in proof of work, and in proof of stake?In proof of stake, it is easy. There already is an "active validator set" that is kept track of in the state, and one can simply sample from this set directly. Either an in-protocol algorithm runs and chooses 150 validators for each shard, or each validator independently runs an algorithm that uses a common source of randomness to (provably) determine which shard they are at any given time. Note that it is very important that the sampling assignment is "compulsory"; validators do not have a choice of what shard they go into. If validators could choose, then attackers with small total stake could concentrate their stake onto one shard and attack it, thereby eliminating the system's security.In proof of work, it is more difficult, as with "direct" proof of work schemes one cannot prevent miners from applying their work to a given shard. It may be possible to use proof-of-file-access forms of proof of work to lock individual miners to individual shards, but it is hard to ensure that miners cannot quickly download or generate data that can be used for other shards and thus circumvent such a mechanism. The best known approach is through a technique invented by Dominic Williams called "puzzle towers", where miners first perform proof of work on a common chain, which then inducts them into a proof of stake-style validator pool, and the validator pool is then sampled just as in the proof-of-stake case.One possible intermediate route might look as follows. Miners can spend a large (O(c)-sized) amount of work to create a new "cryptographic identity". The precise value of the proof of work solution then chooses which shard they have to make their next block on. They can then spend an O(1)-sized amount of work to create a block on that shard, and the value of that proof of work solution determines which shard they can work on next, and so on8. Note that all of these approaches make proof of work "stateful" in some way; the necessity of this is fundamental.How is the randomness for random sampling generated?First of all, it is important to note that even if random number generation is heavily exploitable, this is not a fatal flaw for the protocol; rather, it simply means that there is a medium to high centralization incentive. The reason is that because the randomness is picking fairly large samples, it is difficult to bias the randomness by more than a certain amount.The simplest way to show this is through the binomial distribution, as described above; if one wishes to avoid a sample of size N being more than 50% corrupted by an attacker, and an attacker has p% of the global stake pool, the chance of the attacker being able to get such a majority during one round is:Here's a table for what this probability would look like in practice for various values of N and p: N = 50 N = 100 N = 150 N = 250 p = 0.4 0.0978 0.0271 0.0082 0.0009 p = 0.33 0.0108 0.0004 1.83 * 10-5 3.98 * 10-8 p = 0.25 0.0001 6.63 * 10-8 4.11 * 10-11 1.81 * 10-17 < p = 0.2 2.09 * 10-6 2.14 * 10-11 2.50 * 10-16 3.96 * 10-26 Hence, for N >= 150, the chance that any given random seed will lead to a sample favoring the attacker is very small indeed11,12. What this means from the perspective of security of randomness is that the attacker needs to have a very large amount of freedom in choosing the random values order to break the sampling process outright. Most vulnerabilities in proof-of-stake randomness do not allow the attacker to simply choose a seed; at worst, they give the attacker many chances to select the most favorable seed out of many pseudorandomly generated options. If one is very worried about this, one can simply set N to a greater value, and add a moderately hard key-derivation function to the process of computing the randomness, so that it takes more than 2100 computational steps to find a way to bias the randomness sufficiently.Now, let's look at the risk of attacks being made that try to influence the randomness more marginally, for purposes of profit rather than outright takeover. For example, suppose that there is an algorithm which pseudorandomly selects 1000 validators out of some very large set (each validator getting a reward of $1), an attacker has 10% of the stake so the attacker's average "honest" revenue 100, and at a cost of $1 the attacker can manipulate the randomness to "re-roll the dice" (and the attacker can do this an unlimited number of times).Due to the central limit theorem, the standard deviation of the number of samples, and based on other known results in math the expected maximum of N random samples is slightly under M + S * sqrt(2 * log(N)) where M is the mean and S is the standard deviation. Hence the reward for manipulating the randomness and effectively re-rolling the dice (i.e. increasing N) drops off sharply, e.g. with 0 re-trials your expected reward is $100, with one re-trial it's $105.5, with two it's $108.5, with three it's $110.3, with four it's $111.6, with five it's $112.6 and with six it's $113.5. Hence, after five retrials it stops being worth it. As a result, an economically motivated attacker with ten percent of stake will (socially wastefully) spend $5 to get an additional revenue of $13, for a net surplus of $8.However, this kind of logic assumes that one single round of re-rolling the dice is expensive. Many older proof of stake algorithms have a "stake grinding" vulnerability where re-rolling the dice simply means making a computation locally on one's computer; algorithms with this vulnerability are certainly unacceptable in a sharding context. Newer algorithms (see the "validator selection" section in the proof of stake FAQ) have the property that re-rolling the dice can only be done by voluntarily giving up one's spot in the block creation process, which entails giving up rewards and fees. The best way to mitigate the impact of marginal economically motivated attacks on sample selection is to find ways to increase this cost. One method to increase the cost by a factor of sqrt(N) from N rounds of voting is the majority-bit method devised by Iddo Bentov.Another form of random number generation that is not exploitable by minority coalitions is the deterministic threshold signature approach most researched and advocated by Dominic Williams. The strategy here is to use a deterministic threshold signature to generate the random seed from which samples are selected. Deterministic threshold signatures have the property that the value is guaranteed to be the same regardless of which of a given set of participants provides their data to the algorithm, provided that at least ⅔ of participants do participate honestly. This approach is more obviously not economically exploitable and fully resistant to all forms of stake-grinding, but it has several weaknesses:It relies on more complex cryptography (specifically, elliptic curves and pairings). Other approaches rely on nothing but the random-oracle assumption for common hash algorithms. It fails when many validators are offline. A desired goal for public blockchains is to be able to survive very large portions of the network simultaneously disappearing, as long as a majority of the remaining nodes is honest; deterministic threshold signature schemes at this point cannot provide this property. It's not secure in a bribing attacker or coordinated majority model where more than 67% of validators are colluding. The other approaches described in the proof of stake FAQ above still make it expensive to manipulate the randomness, as data from all validators is mixed into the seed and making any manipulation requires either universal collusion or excluding other validators outright. One might argue that the deterministic threshold signature approach works better in consistency-favoring contexts and other approaches work better in availability-favoring contexts.What are the tradeoffs in making sampling more or less frequent?Selection frequency affects just how adaptive adversaries can be for the protocol to still be secure against them; for example, if you believe that an adaptive attack (e.g. dishonest validators who discover that they are part of the same sample banding together and colluding) can happen in 6 hours but not less, then you would be okay with a sampling time of 4 hours but not 12 hours. This is an argument in favor of making sampling happen as quickly as possible.The main challenge with sampling taking place every block is that reshuffling carries a very high amount of overhead. Specifically, verifying a block on a shard requires knowing the state of that shard, and so every time validators are reshuffled, validators need to download the entire state for the new shard(s) that they are in. This requires both a strong state size control policy (i.e. economically ensuring that the size of the state does not grow too large, whether by deleting old accounts, restricting the rate of creating new accounts or a combination of the two) and a fairly long reshuffling time to work well.Currently, the Parity client can download and verify a full Ethereum state snapshot via "warp-sync" in ~2-8 hours, suggesting that reshuffling periods of a few days but not less are safe; perhaps this could be reduced somewhat by shrinking the state size via storage rent but even still reshuffling periods would need to be long, potentially making the system vulnerable to adaptive adversaries.However, there are ways of completely avoiding the tradeoff, choosing the creator of the next collation in each shard with only a few minutes of warning but without adding impossibly high state downloading overhead. This is done by shifting responsibility for state storage, and possibly even state execution, away from collators entirely, and instead assigning the role to either users or an interactive verification protocol.Can we force more of the state to be held user-side so that transactions can be validated without requiring validators to hold all state data?See also: https://ethresear.ch/t/the-stateless-client-concept/172The techniques here tend to involve requiring users to store state data and provide Merkle proofs along with every transaction that they send. A transaction would be sent along with a Merkle proof-of-correct-execution (or "witness"), and this proof would allow a node that only has the state root to calculate the new state root. This proof-of-correct-execution would consist of the subset of objects in the trie that would need to be traversed to access and verify the state information that the transaction must verify; because Merkle proofs are O(log(n)) sized, the proof for a transaction that accesses a constant number of objects would also be O(log(n)) sized.The subset of objects in a Merkle tree that would need to be provided in a Merkle proof of a transaction that accesses several state objectsImplementing this scheme in its pure form has two flaws. First, it introduces O(log(n)) overhead (~10-30x in practice), although one could argue that this O(log(n)) overhead is not as bad as it seems because it ensures that the validator can always simply keep state data in memory and thus it never needs to deal with the overhead of accessing the hard drive9. Second, it can easily be applied if the addresses that are accessed by a transaction are static, but is more difficult to apply if the addresses in question are dynamic - that is, if the transaction execution has code of the form read(f(read(x))) where the address of some state read depends on the execution result of some other state read. In this case, the address that the transaction sender thinks the transaction will be reading at the time that they send the transaction may well differ from the address that is actually read when the transaction is included in a block, and so the Merkle proof may be insufficient10.This can be solved with access lists (think: a list of accounts and subsets of storage tries), which specify statically what data transactions can access, so when a miner receives a transaction with a witness they can determine that the witness contains all of the data the transaction could possibly access or modify. However, this harms censorship resistance, making attacks similar in form to the attempted DAO soft fork possible.Can we split data and execution so that we get the security from rapid shuffling data validation without the overhead of shuffling the nodes that perform state execution?Yes. We can create a protocol where we split up validators into three roles with different incentives (so that the incentives do not overlap): proposers or collators, a.k.a. prolators, notaries and executors. Prollators are responsible for simply building a chain of collations; while notaries verify that the data in the collations is available. Prolators do not need to verify anything state-dependent (e.g. whether or not someone trying to send ETH has enough money). Executors take the chain of collations agreed to by the prolators as given, and then execute the transactions in the collations sequentially and compute the state. If any transaction included in a collation is invalid, executors simply skip over it. This way, validators that verify availability could be reshuffled instantly, and executors could stay on one shard.There would be a light client protocol that allows light clients to determine what the state is based on claims signed by executors, but this protocol is NOT a simple majority-voting consensus. Rather, the protocol is an interactive game with some similarities to Truebit, where if there is great disagreement then light client simply execute specific collations or portions of collations themselves. Hence, light clients can get a correct view of the state even if 90% of the executors in the shard are corrupted, making it much safer to allow executors to be very infrequently reshuffled or even permanently shard-specific.Choosing what goes in to a collation does require knowing the state of that collation, as that is the most practical way to know what will actually pay transaction fees, but this can be solved by further separating the role of collators (who agree on the history) and proposers (who propose individual collations) and creating a market between the two classes of actors; see here for more discussion on this. However, this approach has since been found to be flawed as per this analysis.Can SNARKs and STARKs help?Yes! One can create a second-level protocol where a SNARK, STARK or similar succinct zero knowledge proof scheme is used to prove the state root of a shard chain, and proof creators can be rewarded for this. That said, shard chains to actually agree on what data gets included into the shard chains in the first place is still required.How can we facilitate cross-shard communication?The easiest scenario to satisfy is one where there are very many applications that individually do not have too many users, and which only very occasionally and loosely interact with each other; in this case, applications can live on separate shards and use cross-shard communication via receipts to talk to each other.This typically involves breaking up each transaction into a "debit" and a "credit". For example, suppose that we have a transaction where account A on shard M wishes to send 100 coins to account B on shard N. The steps would looks as follows:Send a transaction on shard M which (i) deducts the balance of A by 100 coins, and (ii) creates a receipt. A receipt is an object which is not saved in the state directly, but where the fact that the receipt was generated can be verified via a Merkle proof. Wait for the first transaction to be included (sometimes waiting for finalization is required; this depends on the system). Send a transaction on shard N which includes the Merkle proof of the receipt from (1). This transaction also checks in the state of shard N to make sure that this receipt is "unspent"; if it is, then it increases the balance of B by 100 coins, and saves in the state that the receipt is spent. Optionally, the transaction in (3) also saves a receipt, which can then be used to perform further actions on shard M that are contingent on the original operation succeeding. In more complex forms of sharding, transactions may in some cases have effects that spread out across several shards and may also synchronously ask for data from the state of multiple shards.What is the train-and-hotel problem?The following example is courtesy of Andrew Miller. Suppose that a user wants to purchase a train ticket and reserve a hotel, and wants to make sure that the operation is atomic - either both reservations succeed or neither do. If the train ticket and hotel booking applications are on the same shard, this is easy: create a transaction that attempts to make both reservations, and throws an exception and reverts everything unless both reservations succeed. If the two are on different shards, however, this is not so easy; even without cryptoeconomic / decentralization concerns, this is essentially the problem of atomic database transactions.With asynchronous messages only, the simplest solution is to first reserve the train, then reserve the hotel, then once both reservations succeed confirm both; the reservation mechanism would prevent anyone else from reserving (or at least would ensure that enough spots are open to allow all reservations to be confirmed) for some period of time. However, this means that the mechanism relies on an extra security assumptions: that cross-shard messages from one shard can get included in another shard within some fixed period of time.With cross-shard synchronous transactions, the problem is easier, but the challenge of creating a sharding solution capable of making cross-shard atomic synchronous transactions is itself decidedly nontrivial; see Vlad Zamfir's presentation which talks about merge blocks.Another solution involves making contracts themselves movable across shards; see the proposed cross-shard locking scheme as well as this proposal where contracts can be "yanked" from one shard to another, allowing two contracts that normally reside on different shards to be temporarily moved to the same shard at which point a synchronous operation between them can happen.What are the concerns about sharding through random sampling in a bribing attacker or coordinated choice model?In a bribing attacker or coordinated choice model, the fact that validators are randomly sampled doesn't matter: whatever the sample is, either the attacker can bribe the great majority of the sample to do as the attacker pleases, or the attacker controls a majority of the sample directly and can direct the sample to perform arbitrary actions at low cost (O(c) cost, to be precise).At that point, the attacker has the ability to conduct 51% attacks against that sample. The threat is further magnified because there is a risk of cross-shard contagion: if the attacker corrupts the state of a shard, the attacker can then start to send unlimited quantities of funds out to other shards and perform other cross-shard mischief. All in all, security in the bribing attacker or coordinated choice model is not much better than that of simply creating O(c) altcoins.How can we improve on this?In the context of state execution, we can use interactive verification protocols that are not randomly sampled majority votes, and that can give correct answers even if 90% of the participants are faulty; see Truebit for an example of how this can be done. For data availability, the problem is harder, though there are several strategies that can be used alongside majority votes to solve it.What is the data availability problem, and how can we use erasure codes to solve it?See https://github.com/ethereum/research/wiki/A-note-on-data-availability-and-erasure-codingCan we remove the need to solve data availability with some kind of fancy cryptographic accumulator scheme?No. Suppose there is a scheme where there exists an object S representing the state (S could possibly be a hash) possibly as well as auxiliary information ("witnesses") held by individual users that can prove the presence of existing state objects (e.g. S is a Merkle root, the witnesses are the branches, though other constructions like RSA accumulators do exist). There exists an updating protocol where some data is broadcasted, and this data changes S to change the contents of the state, and also possibly changes witnesses.Suppose some user has the witnesses for a set of N objects in the state, and M of the objects are updated. After receiving the update information, the user can check the new status of all N objects, and thereby see which M were updated. Hence, the update information itself encoded at least ~M * log(N) bits of information. Hence, the update information that everyone needs for receive to implement the effect of M transactions must necessarily be of size O(M). 14So this means that we can actually create scalable sharded blockchains where the cost of making anything bad happen is proportional to the size of the entire validator set?There is one trivial attack by which an attacker can always burn O(c) capital to temporarily reduce the quality of a shard: spam it by sending transactions with high transaction fees, forcing legitimate users to outbid you to get in. This attack is unavoidable; you could compensate with flexible gas limits, and you could even try "transparent sharding" schemes that try to automatically re-allocate nodes to shards based on usage, but if some particular application is non-parallelizable, Amdahl's law guarantees that there is nothing you can do. The attack that is opened up here (reminder: it only works in the Zamfir model, not honest/uncoordinated majority) is arguably not substantially worse than the transaction spam attack. Hence, we've reached the known limit for the security of a single shard, and there is no value in trying to go further.Let's walk back a bit. Do we actually need any of this complexity if we have instant shuffling? Doesn't instant shuffling basically mean that each shard directly pulls validators from the global validator pool so it operates just like a blockchain, and so sharding doesn't actually introduce any new complexities?Kind of. First of all, it's worth noting that proof of work and simple proof of stake, even without sharding, both have very low security in a bribing attacker model; a block is only truly "finalized" in the economic sense after O(n) time (as if only a few blocks have passed, then the economic cost of replacing the chain is simply the cost of starting a double-spend from before the block in question). Casper solves this problem by adding its finality mechanism, so that the economic security margin immediately increases to the maximum. In a sharded chain, if we want economic finality then we need to come up with a chain of reasoning for why a validator would be willing to make a very strong claim on a chain based solely on a random sample, when the validator itself is convinced that the bribing attacker and coordinated choice models may be true and so the random sample could potentially be corrupted.You mentioned transparent sharding. I'm 12 years old and what is this?Basically, we do not expose the concept of "shards" directly to developers, and do not permanently assign state objects to specific shards. Instead, the protocol has an ongoing built-in load-balancing process that shifts objects around between shards. If a shard gets too big or consumes too much gas it can be split in half; if two shards get too small and talk to each other very often they can be combined together; if all shards get too small one shard can be deleted and its contents moved to various other shards, etc.Imagine if Donald Trump realized that people travel between New York and London a lot, but there's an ocean in the way, so he could just take out his scissors, cut out the ocean, glue the US east coast and Western Europe together and put the Atlantic beside the South Pole - it's kind of like that.What are some advantages and disadvantages of this?Developers no longer need to think about shards There's the possibility for shards to adjust manually to changes in gas prices, rather than relying on market mechanics to increase gas prices in some shards more than others There is no longer a notion of reliable co-placement: if two contracts are put into the same shard so that they can interact with each other, shard changes may well end up separating them More protocol complexity The co-placement problem can be mitigated by introducing a notion of "sequential domains", where contracts may specify that they exist in the same sequential domain, in which case synchronous communication between them will always be possible. In this model a shard can be viewed as a set of sequential domains that are validated together, and where sequential domains can be rebalanced between shards if the protocol determines that it is efficient to do so.How would synchronous cross-shard messages work?The process becomes much easier if you view the transaction history as being already settled, and are simply trying to calculate the state transition function. There are several approaches; one fairly simple approach can be described as follows:A transaction may specify a set of shards that it can operate in In order for the transaction to be effective, it must be included at the same block height in all of these shards. Transactions within a block must be put in order of their hash (this ensures a canonical order of execution) A client on shard X, if it sees a transaction with shards (X, Y), requests a Merkle proof from shard Y verifying (i) the presence of that transaction on shard Y, and (ii) what the pre-state on shard Y is for those bits of data that the transaction will need to access. It then executes the transaction and commits to the execution result. Note that this process may be highly inefficient if there are many transactions with many different "block pairings" in each block; for this reason, it may be optimal to simply require blocks to specify sister shards, and then calculation can be done more efficiently at a per-block level. This is the basis for how such a scheme could work; one could imagine more complex designs. However, when making a new design, it's always important to make sure that low-cost denial of service attacks cannot arbitrarily slow state calculation down.What about semi-asynchronous messages?Vlad Zamfir created a scheme by which asynchronous messages could still solve the "book a train and hotel" problem. This works as follows. The state keeps track of all operations that have been recently made, as well as the graph of which operations were triggered by any given operation (including cross-shard operations). If an operation is reverted, then a receipt is created which can then be used to revert any effect of that operation on other shards; those reverts may then trigger their own reverts and so forth. The argument is that if one biases the system so that revert messages can propagate twice as fast as other kinds of messages, then a complex cross-shard transaction that finishes executing in K rounds can be fully reverted in another K rounds.The overhead that this scheme would introduce has arguably not been sufficiently studied; there may be worst-case scenarios that trigger quadratic execution vulnerabilities. It is clear that if transactions have effects that are more isolated from each other, the overhead of this mechanism is lower; perhaps isolated executions can be incentivized via favorable gas cost rules. All in all, this is one of the more promising research directions for advanced sharding.What are guaranteed cross-shard calls?One of the challenges in sharding is that when a call is made, there is by default no hard protocol-provided guarantee that any asynchronous operations created by that call will be made within any particular timeframe, or even made at all; rather, it is up to some party to send a transaction in the destination shard triggering the receipt. This is okay for many applications, but in some cases it may be problematic for several reasons:There may be no single party that is clearly incentivized to trigger a given receipt. If the sending of a transaction benefits many parties, then there could be tragedy-of-the-commons effects where the parties try to wait longer until someone else sends the transaction (i.e. play "chicken"), or simply decide that sending the transaction is not worth the transaction fees for them individually. Gas prices across shards may be volatile, and in some cases performing the first half of an operation compels the user to "follow through" on it, but the user may have to end up following through at a much higher gas price. This may be exacerbated by DoS attacks and related forms of griefing. Some applications rely on there being an upper bound on the "latency" of cross-shard messages (e.g. the train-and-hotel example). Lacking hard guarantees, such applications would have to have inefficiently large safety margins. One could try to come up with a system where asynchronous messages made in some shard automatically trigger effects in their destination shard after some number of blocks. However, this requires every client on each shard to actively inspect all other shards in the process of calculating the state transition function, which is arguably a source of inefficiency. The best known compromise approach is this: when a receipt from shard A at height height_a is included in shard B at height height_b, if the difference in block heights exceeds MAX_HEIGHT, then all validators in shard B that created blocks from height_a + MAX_HEIGHT + 1 to height_b - 1 are penalized, and this penalty increases exponentially. A portion of these penalties is given to the validator that finally includes the block as a reward. This keeps the state transition function simple, while still strongly incentivizing the correct behavior.Wait, but what if an attacker sends a cross-shard call from every shard into shard X at the same time? Wouldn't it be mathematically impossible to include all of these calls in time?Correct; this is a problem. Here is a proposed solution. In order to make a cross-shard call from shard A to shard B, the caller must pre-purchase "congealed shard B gas" (this is done via a transaction in shard B, and recorded in shard B). Congealed shard B gas has a fast demurrage rate: once ordered, it loses 1/k of its remaining potency every block. A transaction on shard A can then send the congealed shard B gas along with the receipt that it creates, and it can be used on shard B for free. Shard B blocks allocate extra gas space specifically for these kinds of transactions. Note that because of the demurrage rules, there can be at most GAS_LIMIT * k worth of congealed gas for a given shard available at any time, which can certainly be filled within k blocks (in fact, even faster due to demurrage, but we may need this slack space due to malicious validators). In case too many validators maliciously fail to include receipts, we can make the penalties fairer by exempting validators who fill up the "receipt space" of their blocks with as many receipts as possible, starting with the oldest ones.Under this pre-purchase mechanism, a user that wants to perform a cross-shard operation would first pre-purchase gas for all shards that the operation would go into, over-purchasing to take into account the demurrage. If the operation would create a receipt that triggers an operation that consumes 100000 gas in shard B, the user would pre-buy 100000 * e (i.e. 271818) shard-B congealed gas. If that operation would in turn spend 100000 gas in shard C (i.e. two levels of indirection), the user would need to pre-buy 100000 * e^2 (i.e. 738906) shard-C congealed gas. Notice how once the purchases are confirmed, and the user starts the main operation, the user can be confident that they will be insulated from changes in the gas price market, unless validators voluntarily lose large quantities of money from receipt non-inclusion penalties.Congealed gas? This sounds interesting for not just cross-shard operations, but also reliable intra-shard schedulingIndeed; you could buy congealed shard A gas inside of shard A, and send a guaranteed cross-shard call from shard A to itself. Though note that this scheme would only support scheduling at very short time intervals, and the scheduling would not be exact to the block; it would only be guaranteed to happen within some period of time.Does guaranteed scheduling, both intra-shard and cross-shard, help against majority collusions trying to censor transactions?Yes. If a user fails to get a transaction in because colluding validators are filtering the transaction and not accepting any blocks that include it, then the user could send a series of messages which trigger a chain of guaranteed scheduled messages, the last of which reconstructs the transaction inside of the EVM and executes it. Preventing such circumvention techniques is practically impossible without shutting down the guaranteed scheduling feature outright and greatly restricting the entire protocol, and so malicious validators would not be able to do it easily.Could sharded blockchains do a better job of dealing with network partitions?The schemes described in this document would offer no improvement over non-sharded blockchains; realistically, every shard would end up with some nodes on both sides of the partition. There have been calls (e.g. from IPFS's Juan Benet) for building scalable networks with the specific goal that networks can split up into shards as needed and thus continue operating as much as possible under network partition conditions, but there are nontrivial cryptoeconomic challenges in making this work well.One major challenge is that if we want to have location-based sharding so that geographic network partitions minimally hinder intra-shard cohesion (with the side effect of having very low intra-shard latencies and hence very fast intra-shard block times), then we need to have a way for validators to choose which shards they are participating in. This is dangerous, because it allows for much larger classes of attacks in the honest/uncoordinated majority model, and hence cheaper attacks with higher griefing factors in the Zamfir model. Sharding for geographic partition safety and sharding via random sampling for efficiency are two fundamentally different things.Second, more thinking would need to go into how applications are organized. A likely model in a sharded blockchain as described above is for each "app" to be on some shard (at least for small-scale apps); however, if we want the apps themselves to be partition-resistant, then it means that all apps would need to be cross-shard to some extent.One possible route to solving this is to create a platform that offers both kinds of shards - some shards would be higher-security "global" shards that are randomly sampled, and other shards would be lower-security "local" shards that could have properties such as ultra-fast block times and cheaper transaction fees. Very low-security shards could even be used for data-publishing and messaging.What are the unique challenges of pushing scaling past n = O(c^2)?There are several considerations. First, the algorithm would need to be converted from a two-layer algorithm to a stackable n-layer algorithm; this is possible, but is complex. Second, n / c (i.e. the ratio between the total computation load of the network and the capacity of one node) is a value that happens to be close to two constants: first, if measured in blocks, a timespan of several hours, which is an acceptable "maximum security confirmation time", and second, the ratio between rewards and deposits (an early computation suggests a 32 ETH deposit size and a 0.05 ETH block reward for Casper). The latter has the consequence that if rewards and penalties on a shard are escalated to be on the scale of validator deposits, the cost of continuing an attack on a shard will be O(n) in size.Going above c^2 would likely entail further weakening the kinds of security guarantees that a system can provide, and allowing attackers to attack individual shards in certain ways for extended periods of time at medium cost, although it should still be possible to prevent invalid state from being finalized and to prevent finalized state from being reverted unless attackers are willing to pay an O(n) cost. However, the rewards are large - a super-quadratically sharded blockchain could be used as a general-purpose tool for nearly all decentralized applications, and could sustain transaction fees that makes its use virtually free.What about heterogeneous sharding?Abstracting the execution engine or allowing multiple execution engines to exist results in being able to have a different execution engine for each shard. Due to Casper CBC being able to explore the full tradeoff triangle, it is possible to alter the parameters of the consensus engine for each shard to be at any point of the triangle. However, CBC Casper has not been implemented yet, and heterogeneous sharding is nothing more than an idea at this stage; the specifics of how it would work has not been designed nor implemented. Some shards could be optimized to have fast finality and high throughput, which is important for applications such as EFTPOS transactions, while maybe most could have a moderate or reasonable amount each of finality, throughput and decentralization (number of validating nodes), and applications that are prone to a high fault rate and thus require high security, such as torrent networks, privacy focused email like Proton mail, etc., could optimize for a high decentralization, low finality and high throughput, etc. See also https://twitter.com/VladZamfir/status/932320997021171712 and https://ethresear.ch/t/heterogeneous-sharding/1979/2.Footnotes Merklix tree == Merkle Patricia tree Later proposals from the NUS group do manage to shard state; they do this via the receipt and state-compacting techniques that I describe in later sections in this document. (This is Vitalik Buterin writing as the creator of this Wiki.) There are reasons to be conservative here. Particularly, note that if an attacker comes up with worst-case transactions whose ratio between processing time and block space expenditure (bytes, gas, etc) is much higher than usual, then the system will experience very low performance, and so a safety factor is necessary to account for this possibility. In traditional blockchains, the fact that block processing only takes ~1-5% of block time has the primary role of protecting against centralization risk but serves double duty of protecting against denial of service risk. In the specific case of Bitcoin, its current worst-case known quadratic execution vulnerability arguably limits any scaling at present to ~5-10x, and in the case of Ethereum, while all known vulnerabilities are being or have been removed after the denial-of-service attacks, there is still a risk of further discrepancies particularly on a smaller scale. In Bitcoin NG, the need for the former is removed, but the need for the latter is still there. A further reason to be cautious is that increased state size corresponds to reduced throughput, as nodes will find it harder and harder to keep state data in RAM and so need more and more disk accesses, and databases, which often have an O(log(n)) access time, will take longer and longer to access. This was an important lesson from the last Ethereum denial-of-service attack, which bloated the state by ~10 GB by creating empty accounts and thereby indirectly slowed processing down by forcing further state accesses to hit disk instead of RAM. In sharded blockchains, there may not necessarily be in-lockstep consensus on a single global state, and so the protocol never asks nodes to try to compute a global state root; in fact, in the protocols presented in later sections, each shard has its own state, and for each shard there is a mechanism for committing to the state root for that shard, which represents that shard's state #MEGA If a non-scalable blockchain upgrades into a scalable blockchain, the author's recommended path is that the old chain's state should simply become a single shard in the new chain. For this to be secure, some further conditions must be satisfied; particularly, the proof of work must be non-outsourceable in order to prevent the attacker from determining which other miners' identities are available for some given shard and mining on top of those. Recent Ethereum denial-of-service attacks have proven that hard drive access is a primary bottleneck to blockchain scalability. You could ask: well why don't validators fetch Merkle proofs just-in-time? Answer: because doing so is a ~100-1000ms roundtrip, and executing an entire complex transaction within that time could be prohibitive. One hybrid solution that combines the normal-case efficiency of small samples with the greater robustness of larger samples is a multi-layered sampling scheme: have a consensus between 50 nodes that requires 80% agreement to move forward, and then only if that consensus fails to be reached then fall back to a 250-node sample. N = 50 with an 80% threshold has only a 8.92 * 10-9 failure rate even against attackers with p = 0.4, so this does not harm security at all under an honest or uncoordinated majority model. The probabilities given are for one single shard; however, the random seed affects O(c) shards and the attacker could potentially take over any one of them. If we want to look at O(c) shards simultaneously, then there are two cases. First, if the grinding process is computationally bounded, then this fact does not change the calculus at all, as even though there are now O(c) chances of success per round, checking success takes O(c) times as much work. Second, if the grinding process is economically bounded, then this indeed calls for somewhat higher safety factors (increasing N by 10-20 should be sufficient) although it's important to note that the goal of an attacker in a profit-motivated manipulation attack is to increase their participation across all shards in any case, and so that is the case that we are already investigating. See Parity's Polkadotpaper for further description of how their "fishermen" concept works. For up-to-date info and code for Polkadot, see here. Thanks to Justin Drake for pointing me to cryptographic accumulators, as well as this paper that gives the argument for the impossibility of sublinear batching. See also this thread: https://ethresear.ch/t/accumulators-scalability-of-utxo-blockchains-and-data-availability/176 Further reading related to sharding, and more generally scalability and research, is available here and here.

Notes on Blockchain Governance Notes on Blockchain Governance2017 Dec 17 See all posts Notes on Blockchain Governance In which I argue that "tightly coupled" on-chain voting is overrated, the status quo of "informal governance" as practiced by Bitcoin, Bitcoin Cash, Ethereum, Zcash and similar systems is much less bad than commonly thought, that people who think that the purpose of blockchains is to completely expunge soft mushy human intuitions and feelings in favor of completely algorithmic governance (emphasis on "completely") are absolutely crazy, and loosely coupled voting as done by Carbonvotes and similar systems is underrated, as well as describe what framework should be used when thinking about blockchain governance in the first place.See also: https://medium.com/@Vlad_Zamfir/against-on-chain-governance-a4ceacd040caOne of the more interesting recent trends in blockchain governance is the resurgence of on-chain coin-holder voting as a multi-purpose decision mechanism. Votes by coin holders are sometimes used in order to decide who operates the super-nodes that run a network (eg. DPOS in EOS, NEO, Lisk and other systems), sometimes to vote on protocol parameters (eg. the Ethereum gas limit) and sometimes to vote on and directly implement protocol upgrades wholesale (eg. Tezos). In all of these cases, the votes are automatic - the protocol itself contains all of the logic needed to change the validator set or to update its own rules, and does this automatically in response to the result of votes.Explicit on-chain governance is typically touted as having several major advantages. First, unlike the highly conservative philosophy espoused by Bitcoin, it can evolve rapidly and accept needed technical improvements. Second, by creating an explicit decentralized framework, it avoids the perceived pitfalls of informal governance, which is viewed to either be too unstable and prone to chain splits, or prone to becoming too de-facto centralized - the latter being the same argument made in the famous 1972 essay "Tyranny of Structurelessness".Quoting Tezos documentation:While all blockchains offer financial incentives for maintaining consensus on their ledgers, no blockchain has a robust on-chain mechanism that seamlessly amends the rules governing its protocol and rewards protocol development. As a result, first-generation blockchains empower de facto, centralized core development teams or miners to formulate design choices.And:Yes, but why would you want to make [a minority chain split] easier? Splits destroy network effects.On-chain governance used to select validators also has the benefit that it allows for networks that impose high computational performance requirements on validators without introducing economic centralization risks and other traps of the kind that appear in public blockchains (eg. the validator's dilemma).So far, all in all, on-chain governance seems like a very good bargain.... so what's wrong with it?What is Blockchain Governance?To start off, we need to describe more clearly what the process of "blockchain governance" is. Generally speaking, there are two informal models of governance, that I will call the "decision function" view of governance and the "coordination" view of governance. The decision function view treats governance as a function \(f(x_1, x_2 ... x_n) \rightarrow y\), where the inputs are the wishes of various legitimate stakeholders (senators, the president, property owners, shareholders, voters, etc) and the output is the decision. The decision function view is often useful as an approximation, but it clearly frays very easily around the edges: people often can and do break the law and get away with it, sometimes rules are ambiguous, and sometimes revolutions happen - and all three of these possibilities are, at least sometimes, a good thing. And often even behavior inside the system is shaped by incentives created by the possibility of acting outside the system, and this once again is at least sometimes a good thing.The coordination model of governance, in contrast, sees governance as something that exists in layers. The bottom layer is, in the real world, the laws of physics themselves (as a geopolitical realist would say, guns and bombs), and in the blockchain space we can abstract a bit further and say that it is each individual's ability to run whatever software they want in their capacity as a user, miner, stakeholder, validator or whatever other kind of agent a blockchain protocol allows them to be. The bottom layer is always the ultimate deciding layer; if, for example, all Bitcoin users wake up one day and decides to edit their clients' source code and replace the entire code with an Ethereum client that listens to balances of a particular ERC20 token contract, then that means that that ERC20 token is bitcoin. The bottom layer's ultimate governing power cannot be stopped, but the actions that people take on this layer can be influenced by the layers above it.The second (and crucially important) layer is coordination institutions. The purpose of a coordination institution is to create focal points around how and when individuals should act in order to better coordinate behavior. There are many situations, both in blockchain governance and in real life, where if you act in a certain way alone, you are likely to get nowhere (or worse), but if everyone acts together a desired result can be achieved. An abstract coordination game. You benefit heavily from making the same move as everyone else.In these cases, it's in your interest to go if everyone else is going, and stop if everyone else is stopping. You can think of coordination institutions as putting up green or red flags in the air saying "go" or "stop", with an established culture that everyone watches these flags and (usually) does what they say. Why do people have the incentive to follow these flags? Because everyone else is already following these flags, and you have the incentive to do the same thing as what everyone else is doing. A Byzantine general rallying his troops forward. The purpose of this isn't just to make the soldiers feel brave and excited, but also to reassure them that everyone else feels brave and excited and will charge forward as well, so an individual soldier is not just committing suicide by charging forward alone.Strong claim: this concept of coordination flags encompasses all that we mean by "governance"; in scenarios where coordination games (or more generally, multi-equilibrium games) do not exist, the concept of governance is meaningless.In the real world, military orders from a general function as a flag, and in the blockchain world, the simplest example of such a flag is the mechanism that tells people whether or not a hard fork "is happening". Coordination institutions can be very formal, or they can be informal, and often give suggestions that are ambiguous. Flags would ideally always be either red or green, but sometimes a flag might be yellow, or even holographic, appearing green to some participants and yellow or red to others. Sometimes that are also multiple flags that conflict with each other.The key questions of governance thus become:What should layer 1 be? That is, what features should be set up in the initial protocol itself, and how does this influence the ability to make formulaic (ie. decision-function-like) protocol changes, as well as the level of power of different kinds of agents to act in different ways? What should layer 2 be? That is, what coordination institutions should people be encouraged to care about? The Role of Coin VotingEthereum also has a history with coin voting, including:DAO proposal votes: https://daostats.github.io/proposals.html The DAO Carbonvote: http://v1.carbonvote.com/ The EIP 186/649/669 Carbonvote: http://carbonvote.com/ These three are all examples of loosely coupled coin voting, or coin voting as a layer 2 coordination institution. Ethereum does not have any examples of tightly coupled coin voting (or, coin voting as a layer 1 in-protocol feature), though it does have an example of tightly coupled miner voting: miners' right to vote on the gas limit. Clearly, tightly coupled voting and loosely coupled voting are competitors in the governance mechanism space, so it's worth dissecting: what are the advantages and disadvantages of each one?Assuming zero transaction costs, and if used as a sole governance mechanism, the two are clearly equivalent. If a loosely coupled vote says that change X should be implemented, then that will serve as a "green flag" encouraging everyone to download the update; if a minority wants to rebel, they will simply not download the update. If a tightly coupled vote implements change X, then the change happens automatically, and if a minority wants to rebel they can install a hard fork update that cancels the change. However, there clearly are nonzero transaction costs associated with making a hard fork, and this leads to some very important differences.One very simple, and important, difference is that tightly coupled voting creates a default in favor of the blockchain adopting what the majority wants, requiring minorities to exert great effort to coordinate a hard fork to preserve a blockchain's existing properties, whereas loosely coupled voting is only a coordination tool, and still requires users to actually download and run the software that implements any given fork. But there are also many other differences. Now, let us go through some arguments against voting, and dissect how each argument applies to voting as layer 1 and voting as layer 2.Low Voter ParticipationOne of the main criticisms of coin voting mechanisms so far is that, no matter where they are tried, they tend to have very low voter participation. The DAO Carbonvote only had a voter participation rate of 4.5%: Additionally, wealth distribution is very unequal, and the results of these two factors together are best described by this image created by a critic of the DAO fork: The EIP 186 Carbonvote had ~2.7 million ETH voting. The DAO proposal votes did not fare better, with participation never reaching 10%. And outside of Ethereum things are not sunny either; even in Bitshares, a system where the core social contract is designed around voting, the top delegate in an approval vote only got 17% of the vote, and in Lisk it got up to 30%, though as we will discuss later these systems have other problems of their own.Low voter participation means two things. First, the vote has a harder time achieving a perception of legitimacy, because it only reflects the views of a small percentage of people. Second, an attacker with only a small percentage of all coins can sway the vote. These problems exist regardless of whether the vote is tightly coupled or loosely coupled.Game-Theoretic AttacksAside from "the big hack" that received the bulk of the media attention, the DAO also had a number of much smaller game-theoretic vulnerabilities; this article from HackingDistributed does a good job of summarizing them. But this is only the tip of the iceberg. Even if all of the finer details of a voting mechanism are implemented correctly, voting mechanisms in general have a large flaw: in any vote, the probability that any given voter will have an impact on the result is tiny, and so the personal incentive that each voter has to vote correctly is almost insignificant. And if each person's size of the stake is small, their incentive to vote correctly is insignificant squared. Hence, a relatively small bribe spread out across the participants may suffice to sway their decision, possibly in a way that they collectively might quite disapprove of.Now you might say, people are not evil selfish profit-maximizers that will accept a $0.5 bribe to vote to give twenty million dollars to Josh arza just because the above calculation says their individual chance of affecting anything is tiny; rather, they would altruistically refuse to do something that evil. There are two responses to this criticism.First, there are ways to make a "bribe" that are quite plausible; for example, an exchange can offer interest rates for deposits (or, even more ambiguously, use the exchange's own money to build a great interface and features), with the exchange operator using the large quantity of deposits to vote as they wish. Exchanges profit from chaos, so their incentives are clearly quite misaligned with users and coin holders.Second, and more damningly, in practice it seems like people, at least in their capacity as crypto token holders, are profit maximizers, and seem to see nothing evil or selfish about taking a bribe or two. As "Exhibit A", we can look at the situation with Lisk, where the delegate pool seems to have been successfully captured by two major "political parties" that explicitly bribe coin holders to vote for them, and also require each member in the pool to vote for all the others.Here's LiskElite, with 55 members (out of a total 101): Here's LiskGDT, with 33 members: And as "Exhibit B" some voter bribes being paid out in Ark: Here, note that there is a key difference between tightly coupled and loosely coupled votes. In a loosely coupled vote, direct or indirect vote bribing is also possible, but if the community agrees that some given proposal or set of votes constitutes a game-theoretic attack, they can simply socially agree to ignore it. And in fact this has kind of already happened - the Carbonvote contains a blacklist of addresses corresponding to known exchange addresses, and votes from these addresses are not counted. In a tightly coupled vote, there is no way to create such a blacklist at protocol level, because agreeing who is part of the blacklist is itself a blockchain governance decision. But since the blacklist is part of a community-created voting tool that only indirectly influences protocol changes, voting tools that contain bad blacklists can simply be rejected by the community.It's worth noting that this section is not a prediction that all tightly coupled voting systems will quickly succumb to bribe attacks. It's entirely possible that many will survive for one simple reason: all of these projects have founders or foundations with large premines, and these act as large centralized actors that are interested in their platforms' success that are not vulnerable to bribes, and hold enough coins to outweigh most bribe attacks. However, this kind of centralized trust model, while arguably useful in some contexts in a project's early stages, is clearly one that is not sustainable in the long term.Non-RepresentativenessAnother important objection to voting is that coin holders are only one class of user, and may have interests that collide with those of other users. In the case of pure cryptocurrencies like Bitcoin, store-of-value use ("hodling") and medium-of-exchange use ("buying coffees") are naturally in conflict, as the store-of-value prizes security much more than the medium-of-exchange use case, which more strongly values usability. With Ethereum, the conflict is worse, as there are many people who use Ethereum for reasons that have nothing to do with ether (see: cryptokitties), or even value-bearing digital assets in general (see: ENS).Additionally, even if coin holders are the only relevant class of user (one might imagine this to be the case in a cryptocurrency where there is an established social contract that its purpose is to be the next digital gold, and nothing else), there is still the challenge that a coin holder vote gives a much greater voice to wealthy coin holders than to everyone else, opening the door for centralization of holdings to lead to unencumbered centralization of decision making. Or, in other words... And if you want to see a review of a project that seems to combine all of these disadvantages at the same time, see this: https://btcgeek.com/bitshares-trying-memorycoin-year-ago-disastrous-ends/.This criticism applies to both tightly coupled and loosely coupled voting equally; however, loosely coupled voting is more amenable to compromises that mitigate its unrepresentativeness, and we will discuss this more later.CentralizationLet's look at the existing live experiment that we have in tightly coupled voting on Ethereum, the gas limit. Here's the gas limit evolution over the past two years: You might notice that the general feel of the curve is a bit like another chart that may be quite familiar to you: Basically, they both look like magic numbers that are created and repeatedly renegotiated by a fairly centralized group of guys sitting together in a room. What's happening in the first case? Miners are generally following the direction favored by the community, which is itself gauged via social consensus aids similar to those that drive hard forks (core developer support, Reddit upvotes, etc; in Ethereum, the gas limit has never gotten controversial enough to require anything as serious as a coin vote).Hence, it is not at all clear that voting will be able to deliver results that are actually decentralized, if voters are not technically knowledgeable and simply defer to a single dominant tribe of experts. This criticism once again applies to tightly coupled and loosely coupled voting equally.Update: since writing this, it seems like Ethereum miners managed to up the gas limit from 6.7 million to 8 million all without even discussing it with the core developers or the Ethereum Foundation. So there is hope; but it takes a lot of hard community building and other grueling non-technical work to get to that point.Digital ConstitutionsOne approach that has been suggested to mitigate the risk of runaway bad governance algorithms is "digital constitutions" that mathematically specify desired properties that the protocol should have, and require any new code changes to come with a computer-verifiable proof that they satisfy these properties. This seems like a good idea at first, but this too should, in my opinion, be viewed skeptically.In general, the idea of having norms about protocol properties, and having these norms serve the function of one of the coordination flags, is a very good one. This allows us to enshrine core properties of a protocol that we consider to be very important and valuable, and make them more difficult to change. However, this is exactly the sort of thing that should be enforced in loosely coupled (ie. layer two), rather than tightly coupled (layer one) form.Basically any meaningful norm is actually quite hard to express in its entirety; this is part of the complexity of value problem. This is true even for something as seemingly unambiguous as the 21 million coin limit. Sure, one can add a line of code saying assert total_supply

A Quick Gasprice Market Analysis A Quick Gasprice Market Analysis2017 Dec 14 See all posts A Quick Gasprice Market Analysis Here is a file that contains data, extracted from geth, about transaction fees in every block between 4710000 and 4730000. For each block, it contains an object of the form:{ "block":4710000, "coinbase":"0x829bd824b016326a401d083b33d092293333a830", "deciles":[40,40.1,44.100030001,44.100030001,44.100030001,44.100030001,44.100030001,44.100030001,50,66.150044,100] ,"free":10248, "timedelta":8 }The "deciles" variable contains 11 values, where the lowest is the lowest gasprice in each block, the next is the gasprice that only 10% of other transaction gasprices are lower than, and so forth; the last is the highest gasprice in each block. This gives us a convenient summary of the distribution of transaction fees that each block contains. We can use this data to perform some interesting analyses.First, a chart of the deciles, taking 50-block moving averages to smooth it out: What we see is a gasprice market that seems to actually stay reasonably stable over the course of more than three days. There are a few occasional spikes, most notably the one around block 4720000, but otherwise the deciles all stay within the same band all the way through. The only exception is the highest gasprice transaction (that red squiggle at the top left), which fluctuates wildly because it can be pushed upward by a single very-high-gasprice transaction.We can try to interpret the data in another way: by calculating, for each gasprice level, the average number of blocks that you need to wait until you see a block where the lowest gasprice included is lower than that gasprice. Assuming that miners are rational and all have the same view (implying that if the lowest gasprice in a block is X, then that means there are no more transactions with gasprices above X waiting to be included), this might be a good proxy for the average amount of time that a transaction sender needs to wait to get included if they use that gasprice. The stats are: There is clear clustering going on at the 4, 10 and 20 levels; it seems to be an underexploited strategy to send transactions with fees slightly above these levels, getting in before the crowd of transactions right at the level but only paying a little more.However, there is quite a bit of evidence that miners do not have the same view; that is, some miners see a very different set of transactions from other miners. First of all, we can filter blocks by miner address, and check what the deciles of each miner are. Here is the output of this data, splitting by 2000-block ranges so we can spot behavior that is consistent across the entire period, and filtering out miners that mine less than 10 blocks in any period, as well as filtering out blocks with more 21000 free gas (high levels of free gas may signify an abnormally high minimum gas price policy, like for example 0x6a7a43be33ba930fe58f34e07d0ad6ba7adb9b1f at ~40 gwei and 0xb75d1e62b10e4ba91315c4aa3facc536f8a922f5 at ~10 gwei). We get:0x829bd824b016326a401d083b33d092293333a830 [30, 28, 27, 21, 28, 34, 23, 24, 32, 32] 0xea674fdde714fd979de3edf0f56aa9716b898ec8 [17, 11, 10, 15, 17, 23, 17, 13, 16, 17] 0x5a0b54d5dc17e0aadc383d2db43b0a0d3e029c4c [31, 17, 20, 18, 16, 27, 21, 15, 21, 21] 0x52bc44d5378309ee2abf1539bf71de1b7d7be3b5 [20, 16, 19, 14, 17, 18, 17, 14, 15, 15] 0xb2930b35844a230f00e51431acae96fe543a0347 [21, 17, 19, 17, 17, 25, 17, 16, 19, 19] 0x180ba8f73897c0cb26d76265fc7868cfd936e617 [13, 13, 15, 18, 12, 26, 16, 13, 20, 20] 0xf3b9d2c81f2b24b0fa0acaaa865b7d9ced5fc2fb [26, 25, 23, 21, 22, 28, 25, 24, 26, 25] 0x4bb96091ee9d802ed039c4d1a5f6216f90f81b01 [17, 21, 17, 14, 21, 32, 14, 14, 19, 23] 0x2a65aca4d5fc5b5c859090a6c34d164135398226 [26, 24, 20, 16, 22, 33, 20, 18, 24, 24]The first miner is consistently higher than the others; the last is also higher than average, and the second is consistently among the lowest.Another thing we can look at is timestamp differences - the difference between a block's timestamp and its parent. There is a clear correlation between timestamp difference and lowest gasprice: This makes a lot of sense, as a block that comes right after another block should be cleaning up only the transactions that are too low in gasprice for the parent block to have included, and a block that comes a long time after its predecessor would have many more not-yet-included transactions to choose from. The differences are large, suggesting that a single block is enough to bite off a very substantial chunk of the unconfirmed transaction pool, adding to the evidence that most transactions are included quite quickly.However, if we look at the data in more detail, we see very many instances of blocks with low timestamp differences that contain many transactions with higher gasprices than their parents. Sometimes we do see blocks that actually look like they clean up what their parents could not, like this:, ,But sometimes we see this:, And sometimes we see miners suddenly including many 1-gwei transactions:, This strongly suggests that a miner including transactions with gasprice X should NOT be taken as evidence that there are not still many transactions with gasprice higher than X left to process. This is likely because of imperfections in network propagation.In general, however, what we see seems to be a rather well-functioning fee market, though there is still room to improve in fee estimation and, most importantly of all, continuing to work hard to improve base-chain scalability so that more transactions can get included in the first place.

STARKs, Part II: Thank Goodness It's FRI-day STARKs, Part II: Thank Goodness It's FRI-day2017 Nov 22 See all posts STARKs, Part II: Thank Goodness It's FRI-day Special thanks to Eli Ben-Sasson for ongoing help and explanations, and Justin Drake for reviewingIn the last part of this series, we talked about how you can make some pretty interesting succinct proofs of computation, such as proving that you have computed the millionth Fibonacci number, using a technique involving polynomial composition and division. However, it rested on one critical ingredient: the ability to prove that at least the great majority of a given large set of points are on the same low-degree polynomial. This problem, called "low-degree testing", is perhaps the single most complex part of the protocol.We'll start off by once again re-stating the problem. Suppose that you have a set of points, and you claim that they are all on the same polynomial, with degree less than \(D\) (ie. \(deg < 2\) means they're on the same line, \(deg < 3\) means they're on the same line or parabola, etc). You want to create a succinct probabilistic proof that this is actually true. Left: points all on the same \(deg < 3\) polynomial. Right: points not on the same \(deg < 3\) polynomialIf you want to verify that the points are all on the same degree \(< D\) polynomial, you would have to actually check every point, as if you fail to check even one point there is always some chance that that point will not be on the polynomial even if all the others are. But what you can do is probabilistically check that at least some fraction (eg. 90%) of all the points are on the same polynomial. Top left: possibly close enough to a polynomial. Top right: not close enough to a polynomial. Bottom left: somewhat close to two polynomials, but not close enough to either one. Bottom right: definitely not close enough to a polynomial.If you have the ability to look at every point on the polynomial, then the problem is easy. But what if you can only look at a few points - that is, you can ask for whatever specific point you want, and the prover is obligated to give you the data for that point as part of the protocol, but the total number of queries is limited? Then the question becomes, how many points do you need to check to be able to tell with some given degree of certainty?Clearly, \(D\) points is not enough. \(D\) points are exactly what you need to uniquely define a degree \(< D\) polynomial, so any set of points that you receive will correspond to some degree \(< D\) polynomial. As we see in the figure above, however, \(D+1\) points or more do give some indication.The algorithm to check if a given set of values is on the same degree \(< D\) polynomial with \(D+1\) queries is not too complex. First, select a random subset of \(D\) points, and use something like Lagrange interpolation (search for "Lagrange interpolation" here for a more detailed description) to recover the unique degree \(< D\) polynomial that passes through all of them. Then, randomly sample one more point, and check that it is on the same polynomial. Note that this is only a proximity test, because there's always the possibility that most points are on the same low-degree polynomial, but a few are not, and the \(D+1\) sample missed those points entirely. However, we can derive the result that if less than 90% of the points are on the same degree \(< D\) polynomial, then the test will fail with high probability. Specifically, if you make \(D+k\) queries, and if at least some portion \(p\) of the points are not on the same polynomial as the rest of the points, then the test will only pass with probability \((1 - p)^k\).But what if, as in the examples from the previous article, \(D\) is very high, and you want to verify a polynomial's degree with less than \(D\) queries? This is, of course, impossible to do directly, because of the simple argument made above (namely, that any \(k \leq D\) points are all on at least one degree \(< D\) polynomial). However, it's quite possible to do this indirectly by providing auxiliary data, and achieve massive efficiency gains by doing so. And this is exactly what new protocols like FRI ("Fast RS IOPP", RS = "Reed-Solomon", IOPP = "Interactive Oracle Proofs of Proximity"), and similar earlier designs called probabilistically checkable proofs of proximity (PCPPs), try to achieve.A First Look at SublinearityTo prove that this is at all possible, we'll start off with a relatively simple protocol, with fairly poor tradeoffs, but that still achieves the goal of sublinear verification complexity - that is, you can prove proximity to a degree \(< D\) polynomial with less than \(D\) queries (and, for that matter, less than \(O(D)\) computation to verify the proof).The idea is as follows. Suppose there are N points (we'll say \(N\) = 1 billion), and they are all on a degree \(