找到
1087
篇与
heyuan
相关的结果
-
 Understanding PLONK Understanding PLONK2019 Sep 22 See all posts Understanding PLONK Special thanks to Justin Drake, Karl Floersch, Hsiao-wei Wang, Barry Whitehat, Dankrad Feist, Kobi Gurkan and Zac Williamson for reviewVery recently, Ariel Gabizon, Zac Williamson and Oana Ciobotaru announced a new general-purpose zero-knowledge proof scheme called PLONK, standing for the unwieldy quasi-backronym "Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge". While improvements to general-purpose zero-knowledge proof protocols have been coming for years, what PLONK (and the earlier but more complex SONIC and the more recent Marlin) bring to the table is a series of enhancements that may greatly improve the usability and progress of these kinds of proofs in general.The first improvement is that while PLONK still requires a trusted setup procedure similar to that needed for the SNARKs in Zcash, it is a "universal and updateable" trusted setup. This means two things: first, instead of there being one separate trusted setup for every program you want to prove things about, there is one single trusted setup for the whole scheme after which you can use the scheme with any program (up to some maximum size chosen when making the setup). Second, there is a way for multiple parties to participate in the trusted setup such that it is secure as long as any one of them is honest, and this multi-party procedure is fully sequential: first one person participates, then the second, then the third... The full set of participants does not even need to be known ahead of time; new participants could just add themselves to the end. This makes it easy for the trusted setup to have a large number of participants, making it quite safe in practice.The second improvement is that the "fancy cryptography" it relies on is one single standardized component, called a "polynomial commitment". PLONK uses "Kate commitments", based on a trusted setup and elliptic curve pairings, but you can instead swap it out with other schemes, such as FRI (which would turn PLONK into a kind of STARK) or DARK (based on hidden-order groups). This means the scheme is theoretically compatible with any (achievable) tradeoff between proof size and security assumptions. What this means is that use cases that require different tradeoffs between proof size and security assumptions (or developers that have different ideological positions about this question) can still share the bulk of the same tooling for "arithmetization" - the process for converting a program into a set of polynomial equations that the polynomial commitments are then used to check. If this kind of scheme becomes widely adopted, we can thus expect rapid progress in improving shared arithmetization techniques.How PLONK worksLet us start with an explanation of how PLONK works, in a somewhat abstracted format that focuses on polynomial equations without immediately explaining how those equations are verified. A key ingredient in PLONK, as is the case in the QAPs used in SNARKs, is a procedure for converting a problem of the form "give me a value \(X\) such that a specific program \(P\) that I give you, when evaluated with \(X\) as an input, gives some specific result \(Y\)" into the problem "give me a set of values that satisfies a set of math equations". The program \(P\) can represent many things; for example the problem could be "give me a solution to this sudoku", which you would encode by setting \(P\) to be a sudoku verifier plus some initial values encoded and setting \(Y\) to \(1\) (ie. "yes, this solution is correct"), and a satisfying input \(X\) would be a valid solution to the sudoku. This is done by representing \(P\) as a circuit with logic gates for addition and multiplication, and converting it into a system of equations where the variables are the values on all the wires and there is one equation per gate (eg. \(x_6 = x_4 \cdot x_7\) for multiplication, \(x_8 = x_5 + x_9\) for addition).Here is an example of the problem of finding \(x\) such that \(P(x) = x^3 + x + 5 = 35\) (hint: \(x = 3\)): We can label the gates and wires as follows: On the gates and wires, we have two types of constraints: gate constraints (equations between wires attached to the same gate, eg. \(a_1 \cdot b_1 = c_1\)) and copy constraints (claims about equality of different wires anywhere in the circuit, eg. \(a_0 = a_1 = b_1 = b_2 = a_3\) or \(c_0 = a_1\)). We will need to create a structured system of equations, which will ultimately reduce to a very small number of polynomial equations, to represent both.In PLONK, the setup for these equations is as follows. Each equation is of the following form (think: \(L\) = left, \(R\) = right, \(O\) = output, \(M\) = multiplication, \(C\) = constant):\[ \left(Q_}\right) a_+\left(Q_}\right) b_+\left(Q_}\right) c_+\left(Q_}\right) a_ b_+Q_}=0 \]Each \(Q\) value is a constant; the constants in each equation (and the number of equations) will be different for each program. Each small-letter value is a variable, provided by the user: \(a_i\) is the left input wire of the \(i\)'th gate, \(b_i\) is the right input wire, and \(c_i\) is the output wire of the \(i\)'th gate. For an addition gate, we set:\[ Q_}=1, Q_}=1, Q_}=0, Q_}=-1, Q_}=0 \]Plugging these constants into the equation and simplifying gives us \(a_i + b_i - c_i = 0\), which is exactly the constraint that we want. For a multiplication gate, we set:\[ Q_}=0, Q_}=0, Q_}=1, Q_}=-1, Q_}=0 \]For a constant gate setting \(a_i\) to some constant \(x\), we set:\[ Q_=1, Q_=0, Q_=0, Q_=0, Q_=-x \]You may have noticed that each end of a wire, as well as each wire in a set of wires that clearly must have the same value (eg. \(x\)), corresponds to a distinct variable; there's nothing so far forcing the output of one gate to be the same as the input of another gate (what we call "copy constraints"). PLONK does of course have a way of enforcing copy constraints, but we'll get to this later. So now we have a problem where a prover wants to prove that they have a bunch of \(x_, x_\) and \(x_\) values that satisfy a bunch of equations that are of the same form. This is still a big problem, but unlike "find a satisfying input to this computer program" it's a very structured big problem, and we have mathematical tools to "compress" it.From linear systems to polynomialsIf you have read about STARKs or QAPs, the mechanism described in this next section will hopefully feel somewhat familiar, but if you have not that's okay too. The main ingredient here is to understand a polynomial as a mathematical tool for encapsulating a whole lot of values into a single object. Typically, we think of polynomials in "coefficient form", that is an expression like:\[ y=x^-5 x^+7 x-2 \]But we can also view polynomials in "evaluation form". For example, we can think of the above as being "the" degree \(< 4\) polynomial with evaluations \((-2, 1, 0, 1)\) at the coordinates \((0, 1, 2, 3)\) respectively. Now here's the next step. Systems of many equations of the same form can be re-interpreted as a single equation over polynomials. For example, suppose that we have the system:\[ \begin-x_+3 x_=8} \\ +4 x_-5 x_=5} \\ -x_-x_=-2}\end \]Let us define four polynomials in evaluation form: \(L(x)\) is the degree \(< 3\) polynomial that evaluates to \((2, 1, 8)\) at the coordinates \((0, 1, 2)\), and at those same coordinates \(M(x)\) evaluates to \((-1, 4, -1)\), \(R(x)\) to \((3, -5, -1)\) and \(O(x)\) to \((8, 5, -2)\) (it is okay to directly define polynomials in this way; you can use Lagrange interpolation to convert to coefficient form). Now, consider the equation:\[ L(x) \cdot x_+M(x) \cdot x_+R(x) \cdot x_-O(x)=Z(x) H(x) \]Here, \(Z(x)\) is shorthand for \((x-0) \cdot (x-1) \cdot (x-2)\) - the minimal (nontrivial) polynomial that returns zero over the evaluation domain \((0, 1, 2)\). A solution to this equation (\(x_1 = 1, x_2 = 6, x_3 = 4, H(x) = 0\)) is also a solution to the original system of equations, except the original system does not need \(H(x)\). Notice also that in this case, \(H(x)\) is conveniently zero, but in more complex cases \(H\) may need to be nonzero.So now we know that we can represent a large set of constraints within a small number of mathematical objects (the polynomials). But in the equations that we made above to represent the gate wire constraints, the \(x_1, x_2, x_3\) variables are different per equation. We can handle this by making the variables themselves polynomials rather than constants in the same way. And so we get:\[ Q_(x) a(x)+Q_(x) b(x)+Q_(x) c(x)+Q_(x) a(x) b(x)+Q_(x)=0 \]As before, each \(Q\) polynomial is a parameter that can be generated from the program that is being verified, and the \(a\), \(b\), \(c\) polynomials are the user-provided inputs.Copy constraintsNow, let us get back to "connecting" the wires. So far, all we have is a bunch of disjoint equations about disjoint values that are independently easy to satisfy: constant gates can be satisfied by setting the value to the constant and addition and multiplication gates can simply be satisfied by setting all wires to zero! To make the problem actually challenging (and actually represent the problem encoded in the original circuit), we need to add an equation that verifies "copy constraints": constraints such as \(a(5) = c(7)\), \(c(10) = c(12)\), etc. This requires some clever trickery.Our strategy will be to design a "coordinate pair accumulator", a polynomial \(p(x)\) which works as follows. First, let \(X(x)\) and \(Y(x)\) be two polynomials representing the \(x\) and \(y\) coordinates of a set of points (eg. to represent the set \(((0, -2), (1, 1), (2, 0), (3, 1))\) you might set \(X(x) = x\) and \(Y(x) = x^3 - 5x^2 + 7x - 2)\). Our goal will be to let \(p(x)\) represent all the points up to (but not including) the given position, so \(p(0)\) starts at \(1\), \(p(1)\) represents just the first point, \(p(2)\) the first and the second, etc. We will do this by "randomly" selecting two constants, \(v_1\) and \(v_2\), and constructing \(p(x)\) using the constraints \(p(0) = 1\) and \(p(x+1) = p(x) \cdot (v_1 + X(x) + v_2 \cdot Y(x))\) at least within the domain \((0, 1, 2, 3)\).For example, letting \(v_1 = 3\) and \(v_2 = 2\), we get: X(x) 0 1 2 3 4 \(Y(x)\) -2 1 0 1 \(v_1 + X(x) + v_2 \cdot Y(x)\) -1 6 5 8 \(p(x)\) 1 -1 -6 -30 -240 Notice that (aside from the first column) every \(p(x)\) value equals the value to the left of it multiplied by the value to the left and above it. The result we care about is \(p(4) = -240\). Now, consider the case where instead of \(X(x) = x\), we set \(X(x) = \frac x^3 - 4x^2 + \fracx\) (that is, the polynomial that evaluates to \((0, 3, 2, 1)\) at the coordinates \((0, 1, 2, 3)\)). If you run the same procedure, you'll find that you also get \(p(4) = -240\). This is not a coincidence (in fact, if you randomly pick \(v_1\) and \(v_2\) from a sufficiently large field, it will almost never happen coincidentally). Rather, this happens because \(Y(1) = Y(3)\), so if you "swap the \(X\) coordinates" of the points \((1, 1)\) and \((3, 1)\) you're not changing the set of points, and because the accumulator encodes a set (as multiplication does not care about order) the value at the end will be the same.Now we can start to see the basic technique that we will use to prove copy constraints. First, consider the simple case where we only want to prove copy constraints within one set of wires (eg. we want to prove \(a(1) = a(3)\)). We'll make two coordinate accumulators: one where \(X(x) = x\) and \(Y(x) = a(x)\), and the other where \(Y(x) = a(x)\) but \(X'(x)\) is the polynomial that evaluates to the permutation that flips (or otherwise rearranges) the values in each copy constraint; in the \(a(1) = a(3)\) case this would mean the permutation would start \(0 3 2 1 4...\). The first accumulator would be compressing \(((0, a(0)), (1, a(1)), (2, a(2)), (3, a(3)), (4, a(4))...\), the second \(((0, a(0)), (3, a(1)), (2, a(2)), (1, a(3)), (4, a(4))...\). The only way the two can give the same result is if \(a(1) = a(3)\).To prove constraints between \(a\), \(b\) and \(c\), we use the same procedure, but instead "accumulate" together points from all three polynomials. We assign each of \(a\), \(b\), \(c\) a range of \(X\) coordinates (eg. \(a\) gets \(X_a(x) = x\) ie. \(0...n-1\), \(b\) gets \(X_b(x) = n+x\), ie. \(n...2n-1\), \(c\) gets \(X_c(x) = 2n+x\), ie. \(2n...3n-1\). To prove copy constraints that hop between different sets of wires, the "alternate" \(X\) coordinates would be slices of a permutation across all three sets. For example, if we want to prove \(a(2) = b(4)\) with \(n = 5\), then \(X'_a(x)\) would have evaluations \(\\) and \(X'_b(x)\) would have evaluations \(\\) (notice the \(2\) and \(9\) flipped, where \(9\) corresponds to the \(b_4\) wire). Often, \(X'_a(x)\), \(X'_b(x)\) and \(X'_c(x)\) are also called \(\sigma_a(x)\), \(\sigma_b(x)\) and \(\sigma_c(x)\).We would then instead of checking equality within one run of the procedure (ie. checking \(p(4) = p'(4)\) as before), we would check the product of the three different runs on each side:\[ p_(n) \cdot p_(n) \cdot p_(n)=p_^(n) \cdot p_^(n) \cdot p_^(n) \]The product of the three \(p(n)\) evaluations on each side accumulates all coordinate pairs in the \(a\), \(b\) and \(c\) runs on each side together, so this allows us to do the same check as before, except that we can now check copy constraints not just between positions within one of the three sets of wires \(a\), \(b\) or \(c\), but also between one set of wires and another (eg. as in \(a(2) = b(4)\)).And that's all there is to it!Putting it all togetherIn reality, all of this math is done not over integers, but over a prime field; check the section "A Modular Math Interlude" here for a description of what prime fields are. Also, for mathematical reasons perhaps best appreciated by reading and understanding this article on FFT implementation, instead of representing wire indices with \(x=0....n-1\), we'll use powers of \(\omega: 1, \omega, \omega ^2....\omega ^\) where \(\omega\) is a high-order root-of-unity in the field. This changes nothing about the math, except that the coordinate pair accumulator constraint checking equation changes from \(p(x + 1) = p(x) \cdot (v_1 + X(x) + v_2 \cdot Y(x))\) to \(p(\omega \cdot x) = p(x) \cdot (v_1 + X(x) + v_2 \cdot Y(x))\), and instead of using \(0..n-1\), \(n..2n-1\), \(2n..3n-1\) as coordinates we use \(\omega^i, g \cdot \omega^i\) and \(g^2 \cdot \omega^i\) where \(g\) can be some random high-order element in the field.Now let's write out all the equations we need to check. First, the main gate-constraint satisfaction check:\[ Q_(x) a(x)+Q_(x) b(x)+Q_(x) c(x)+Q_(x) a(x) b(x)+Q_(x)=0 \]Then the polynomial accumulator transition constraint (note: think of "\(= Z(x) \cdot H(x)\)" as meaning "equals zero for all coordinates within some particular domain that we care about, but not necessarily outside of it"):\[ \begin(\omega x)-P_(x)\left(v_+x+v_ a(x)\right) =Z(x) H_(x)} \\ }(\omega x)-P_}(x)\left(v_+\sigma_(x)+v_ a(x)\right)=Z(x) H_(x)} \\ (\omega x)-P_(x)\left(v_+g x+v_ b(x)\right)=Z(x) H_(x)} \\ }(\omega x)-P_}(x)\left(v_+\sigma_(x)+v_ b(x)\right)=Z(x) H_(x)} \\ (\omega x)-P_(x)\left(v_+g^ x+v_ c(x)\right)=Z(x) H_(x)} \\ }(\omega x)-P_}(x)\left(v_+\sigma_(x)+v_ c(x)\right)=Z(x) H_(x)}\end \]Then the polynomial accumulator starting and ending constraints:\[ \begin(1)=P_(1)=P_(1)=P_}(1)=P_}(1)=P_}(1)=1} \\ \left(\omega^\right) P_\left(\omega^\right) P_\left(\omega^\right)=P_}\left(\omega^\right) P_}\left(\omega^\right) P_}\left(\omega^\right)}\end \]The user-provided polynomials are:The wire assignments \(a(x), b(x), c(x)\) The coordinate accumulators \(P_a(x), P_b(x), P_c(x), P_(x), P_(x), P_(x)\) The quotients \(H(x)\) and \(H_1(x)...H_6(x)\) The program-specific polynomials that the prover and verifier need to compute ahead of time are:\(Q_L(x), Q_R(x), Q_O(x), Q_M(x), Q_C(x)\), which together represent the gates in the circuit (note that \(Q_C(x)\) encodes public inputs, so it may need to be computed or modified at runtime) The "permutation polynomials" \(\sigma_a(x), \sigma_b(x)\) and \(\sigma_c(x)\), which encode the copy constraints between the \(a\), \(b\) and \(c\) wires Note that the verifier need only store commitments to these polynomials. The only remaining polynomial in the above equations is \(Z(x) = (x - 1) \cdot (x - \omega) \cdot ... \cdot (x - \omega ^)\) which is designed to evaluate to zero at all those points. Fortunately, \(\omega\) can be chosen to make this polynomial very easy to evaluate: the usual technique is to choose \(\omega\) to satisfy \(\omega ^n = 1\), in which case \(Z(x) = x^n - 1\).There is one nuance here: the constraint between \(P_a(\omega^)\) and \(P_a(\omega^i)\) can't be true across the entire circle of powers of \(\omega\); it's almost always false at \(\omega^\) as the next coordinate is \(\omega^n = 1\) which brings us back to the start of the "accumulator"; to fix this, we can modify the constraint to say "either the constraint is true or \(x = \omega^\)", which one can do by multiplying \(x - \omega^\) into the constraint so it equals zero at that point.The only constraint on \(v_1\) and \(v_2\) is that the user must not be able to choose \(a(x), b(x)\) or \(c(x)\) after \(v_1\) and \(v_2\) become known, so we can satisfy this by computing \(v_1\) and \(v_2\) from hashes of commitments to \(a(x), b(x)\) and \(c(x)\).So now we've turned the program satisfaction problem into a simple problem of satisfying a few equations with polynomials, and there are some optimizations in PLONK that allow us to remove many of the polynomials in the above equations that I will not go into to preserve simplicity. But the polynomials themselves, both the program-specific parameters and the user inputs, are big. So the next question is, how do we get around this so we can make the proof short?Polynomial commitmentsA polynomial commitment is a short object that "represents" a polynomial, and allows you to verify evaluations of that polynomial, without needing to actually contain all of the data in the polynomial. That is, if someone gives you a commitment \(c\) representing \(P(x)\), they can give you a proof that can convince you, for some specific \(z\), what the value of \(P(z)\) is. There is a further mathematical result that says that, over a sufficiently big field, if certain kinds of equations (chosen before \(z\) is known) about polynomials evaluated at a random \(z\) are true, those same equations are true about the whole polynomial as well. For example, if \(P(z) \cdot Q(z) + R(z) = S(z) + 5\), then we know that it's overwhelmingly likely that \(P(x) \cdot Q(x) + R(x) = S(x) + 5\) in general. Using such polynomial commitments, we could very easily check all of the above polynomial equations above - make the commitments, use them as input to generate \(z\), prove what the evaluations are of each polynomial at \(z\), and then run the equations with these evaluations instead of the original polynomials. But how do these commitments work?There are two parts: the commitment to the polynomial \(P(x) \rightarrow c\), and the opening to a value \(P(z)\) at some \(z\). To make a commitment, there are many techniques; one example is FRI, and another is Kate commitments which I will describe below. To prove an opening, it turns out that there is a simple generic "subtract-and-divide" trick: to prove that \(P(z) = a\), you prove that\[ \frac \]is also a polynomial (using another polynomial commitment). This works because if the quotient is a polynomial (ie. it is not fractional), then \(x - z\) is a factor of \(P(x) - a\), so \((P(x) - a)(z) = 0\), so \(P(z) = a\). Try it with some polynomial, eg. \(P(x) = x^3 + 2 \cdot x^2 + 5\) with \((z = 6, a = 293)\), yourself; and try \((z = 6, a = 292)\) and see how it fails (if you're lazy, see WolframAlpha here vs here). Note also a generic optimization: to prove many openings of many polynomials at the same time, after committing to the outputs do the subtract-and-divide trick on a random linear combination of the polynomials and the outputs.So how do the commitments themselves work? Kate commitments are, fortunately, much simpler than FRI. A trusted-setup procedure generates a set of elliptic curve points \(G, G \cdot s, G \cdot s^2\) .... \(G \cdot s^n\), as well as \(G_2 \cdot s\), where \(G\) and \(G_2\) are the generators of two elliptic curve groups and \(s\) is a secret that is forgotten once the procedure is finished (note that there is a multi-party version of this setup, which is secure as long as at least one of the participants forgets their share of the secret). These points are published and considered to be "the proving key" of the scheme; anyone who needs to make a polynomial commitment will need to use these points. A commitment to a degree-d polynomial is made by multiplying each of the first d+1 points in the proving key by the corresponding coefficient in the polynomial, and adding the results together.Notice that this provides an "evaluation" of that polynomial at \(s\), without knowing \(s\). For example, \(x^3 + 2x^2+5\) would be represented by \((G \cdot s^3) + 2 \cdot (G \cdot s^2) + 5 \cdot G\). We can use the notation \([P]\) to refer to \(P\) encoded in this way (ie. \(G \cdot P(s)\)). When doing the subtract-and-divide trick, you can prove that the two polynomials actually satisfy the relation by using elliptic curve pairings: check that \(e([P] - G \cdot a, G_2) = e([Q], [x] - G_2 \cdot z)\) as a proxy for checking that \(P(x) - a = Q(x) \cdot (x - z)\).But there are more recently other types of polynomial commitments coming out too. A new scheme called DARK ("Diophantine arguments of knowledge") uses "hidden order groups" such as class groups to implement another kind of polynomial commitment. Hidden order groups are unique because they allow you to compress arbitrarily large numbers into group elements, even numbers much larger than the size of the group element, in a way that can't be "spoofed"; constructions from VDFs to accumulators to range proofs to polynomial commitments can be built on top of this. Another option is to use bulletproofs, using regular elliptic curve groups at the cost of the proof taking much longer to verify. Because polynomial commitments are much simpler than full-on zero knowledge proof schemes, we can expect more such schemes to get created in the future.RecapTo finish off, let's go over the scheme again. Given a program \(P\), you convert it into a circuit, and generate a set of equations that look like this:\[ \left(Q_}\right) a_+\left(Q_}\right) b_+\left(Q_}\right) c_+\left(Q_}\right) a_ b_+Q_}=0 \]You then convert this set of equations into a single polynomial equation:\[ Q_(x) a(x)+Q_(x) b(x)+Q_(x) c(x)+Q_(x) a(x) b(x)+Q_(x)=0 \]You also generate from the circuit a list of copy constraints. From these copy constraints you generate the three polynomials representing the permuted wire indices: \(\sigma_a(x), \sigma_b(x), \sigma_c(x)\). To generate a proof, you compute the values of all the wires and convert them into three polynomials: \(a(x), b(x), c(x)\). You also compute six "coordinate pair accumulator" polynomials as part of the permutation-check argument. Finally you compute the cofactors \(H_i(x)\).There is a set of equations between the polynomials that need to be checked; you can do this by making commitments to the polynomials, opening them at some random \(z\) (along with proofs that the openings are correct), and running the equations on these evaluations instead of the original polynomials. The proof itself is just a few commitments and openings and can be checked with a few equations. And that's all there is to it!
Understanding PLONK Understanding PLONK2019 Sep 22 See all posts Understanding PLONK Special thanks to Justin Drake, Karl Floersch, Hsiao-wei Wang, Barry Whitehat, Dankrad Feist, Kobi Gurkan and Zac Williamson for reviewVery recently, Ariel Gabizon, Zac Williamson and Oana Ciobotaru announced a new general-purpose zero-knowledge proof scheme called PLONK, standing for the unwieldy quasi-backronym "Permutations over Lagrange-bases for Oecumenical Noninteractive arguments of Knowledge". While improvements to general-purpose zero-knowledge proof protocols have been coming for years, what PLONK (and the earlier but more complex SONIC and the more recent Marlin) bring to the table is a series of enhancements that may greatly improve the usability and progress of these kinds of proofs in general.The first improvement is that while PLONK still requires a trusted setup procedure similar to that needed for the SNARKs in Zcash, it is a "universal and updateable" trusted setup. This means two things: first, instead of there being one separate trusted setup for every program you want to prove things about, there is one single trusted setup for the whole scheme after which you can use the scheme with any program (up to some maximum size chosen when making the setup). Second, there is a way for multiple parties to participate in the trusted setup such that it is secure as long as any one of them is honest, and this multi-party procedure is fully sequential: first one person participates, then the second, then the third... The full set of participants does not even need to be known ahead of time; new participants could just add themselves to the end. This makes it easy for the trusted setup to have a large number of participants, making it quite safe in practice.The second improvement is that the "fancy cryptography" it relies on is one single standardized component, called a "polynomial commitment". PLONK uses "Kate commitments", based on a trusted setup and elliptic curve pairings, but you can instead swap it out with other schemes, such as FRI (which would turn PLONK into a kind of STARK) or DARK (based on hidden-order groups). This means the scheme is theoretically compatible with any (achievable) tradeoff between proof size and security assumptions. What this means is that use cases that require different tradeoffs between proof size and security assumptions (or developers that have different ideological positions about this question) can still share the bulk of the same tooling for "arithmetization" - the process for converting a program into a set of polynomial equations that the polynomial commitments are then used to check. If this kind of scheme becomes widely adopted, we can thus expect rapid progress in improving shared arithmetization techniques.How PLONK worksLet us start with an explanation of how PLONK works, in a somewhat abstracted format that focuses on polynomial equations without immediately explaining how those equations are verified. A key ingredient in PLONK, as is the case in the QAPs used in SNARKs, is a procedure for converting a problem of the form "give me a value \(X\) such that a specific program \(P\) that I give you, when evaluated with \(X\) as an input, gives some specific result \(Y\)" into the problem "give me a set of values that satisfies a set of math equations". The program \(P\) can represent many things; for example the problem could be "give me a solution to this sudoku", which you would encode by setting \(P\) to be a sudoku verifier plus some initial values encoded and setting \(Y\) to \(1\) (ie. "yes, this solution is correct"), and a satisfying input \(X\) would be a valid solution to the sudoku. This is done by representing \(P\) as a circuit with logic gates for addition and multiplication, and converting it into a system of equations where the variables are the values on all the wires and there is one equation per gate (eg. \(x_6 = x_4 \cdot x_7\) for multiplication, \(x_8 = x_5 + x_9\) for addition).Here is an example of the problem of finding \(x\) such that \(P(x) = x^3 + x + 5 = 35\) (hint: \(x = 3\)): We can label the gates and wires as follows: On the gates and wires, we have two types of constraints: gate constraints (equations between wires attached to the same gate, eg. \(a_1 \cdot b_1 = c_1\)) and copy constraints (claims about equality of different wires anywhere in the circuit, eg. \(a_0 = a_1 = b_1 = b_2 = a_3\) or \(c_0 = a_1\)). We will need to create a structured system of equations, which will ultimately reduce to a very small number of polynomial equations, to represent both.In PLONK, the setup for these equations is as follows. Each equation is of the following form (think: \(L\) = left, \(R\) = right, \(O\) = output, \(M\) = multiplication, \(C\) = constant):\[ \left(Q_}\right) a_+\left(Q_}\right) b_+\left(Q_}\right) c_+\left(Q_}\right) a_ b_+Q_}=0 \]Each \(Q\) value is a constant; the constants in each equation (and the number of equations) will be different for each program. Each small-letter value is a variable, provided by the user: \(a_i\) is the left input wire of the \(i\)'th gate, \(b_i\) is the right input wire, and \(c_i\) is the output wire of the \(i\)'th gate. For an addition gate, we set:\[ Q_}=1, Q_}=1, Q_}=0, Q_}=-1, Q_}=0 \]Plugging these constants into the equation and simplifying gives us \(a_i + b_i - c_i = 0\), which is exactly the constraint that we want. For a multiplication gate, we set:\[ Q_}=0, Q_}=0, Q_}=1, Q_}=-1, Q_}=0 \]For a constant gate setting \(a_i\) to some constant \(x\), we set:\[ Q_=1, Q_=0, Q_=0, Q_=0, Q_=-x \]You may have noticed that each end of a wire, as well as each wire in a set of wires that clearly must have the same value (eg. \(x\)), corresponds to a distinct variable; there's nothing so far forcing the output of one gate to be the same as the input of another gate (what we call "copy constraints"). PLONK does of course have a way of enforcing copy constraints, but we'll get to this later. So now we have a problem where a prover wants to prove that they have a bunch of \(x_, x_\) and \(x_\) values that satisfy a bunch of equations that are of the same form. This is still a big problem, but unlike "find a satisfying input to this computer program" it's a very structured big problem, and we have mathematical tools to "compress" it.From linear systems to polynomialsIf you have read about STARKs or QAPs, the mechanism described in this next section will hopefully feel somewhat familiar, but if you have not that's okay too. The main ingredient here is to understand a polynomial as a mathematical tool for encapsulating a whole lot of values into a single object. Typically, we think of polynomials in "coefficient form", that is an expression like:\[ y=x^-5 x^+7 x-2 \]But we can also view polynomials in "evaluation form". For example, we can think of the above as being "the" degree \(< 4\) polynomial with evaluations \((-2, 1, 0, 1)\) at the coordinates \((0, 1, 2, 3)\) respectively. Now here's the next step. Systems of many equations of the same form can be re-interpreted as a single equation over polynomials. For example, suppose that we have the system:\[ \begin-x_+3 x_=8} \\ +4 x_-5 x_=5} \\ -x_-x_=-2}\end \]Let us define four polynomials in evaluation form: \(L(x)\) is the degree \(< 3\) polynomial that evaluates to \((2, 1, 8)\) at the coordinates \((0, 1, 2)\), and at those same coordinates \(M(x)\) evaluates to \((-1, 4, -1)\), \(R(x)\) to \((3, -5, -1)\) and \(O(x)\) to \((8, 5, -2)\) (it is okay to directly define polynomials in this way; you can use Lagrange interpolation to convert to coefficient form). Now, consider the equation:\[ L(x) \cdot x_+M(x) \cdot x_+R(x) \cdot x_-O(x)=Z(x) H(x) \]Here, \(Z(x)\) is shorthand for \((x-0) \cdot (x-1) \cdot (x-2)\) - the minimal (nontrivial) polynomial that returns zero over the evaluation domain \((0, 1, 2)\). A solution to this equation (\(x_1 = 1, x_2 = 6, x_3 = 4, H(x) = 0\)) is also a solution to the original system of equations, except the original system does not need \(H(x)\). Notice also that in this case, \(H(x)\) is conveniently zero, but in more complex cases \(H\) may need to be nonzero.So now we know that we can represent a large set of constraints within a small number of mathematical objects (the polynomials). But in the equations that we made above to represent the gate wire constraints, the \(x_1, x_2, x_3\) variables are different per equation. We can handle this by making the variables themselves polynomials rather than constants in the same way. And so we get:\[ Q_(x) a(x)+Q_(x) b(x)+Q_(x) c(x)+Q_(x) a(x) b(x)+Q_(x)=0 \]As before, each \(Q\) polynomial is a parameter that can be generated from the program that is being verified, and the \(a\), \(b\), \(c\) polynomials are the user-provided inputs.Copy constraintsNow, let us get back to "connecting" the wires. So far, all we have is a bunch of disjoint equations about disjoint values that are independently easy to satisfy: constant gates can be satisfied by setting the value to the constant and addition and multiplication gates can simply be satisfied by setting all wires to zero! To make the problem actually challenging (and actually represent the problem encoded in the original circuit), we need to add an equation that verifies "copy constraints": constraints such as \(a(5) = c(7)\), \(c(10) = c(12)\), etc. This requires some clever trickery.Our strategy will be to design a "coordinate pair accumulator", a polynomial \(p(x)\) which works as follows. First, let \(X(x)\) and \(Y(x)\) be two polynomials representing the \(x\) and \(y\) coordinates of a set of points (eg. to represent the set \(((0, -2), (1, 1), (2, 0), (3, 1))\) you might set \(X(x) = x\) and \(Y(x) = x^3 - 5x^2 + 7x - 2)\). Our goal will be to let \(p(x)\) represent all the points up to (but not including) the given position, so \(p(0)\) starts at \(1\), \(p(1)\) represents just the first point, \(p(2)\) the first and the second, etc. We will do this by "randomly" selecting two constants, \(v_1\) and \(v_2\), and constructing \(p(x)\) using the constraints \(p(0) = 1\) and \(p(x+1) = p(x) \cdot (v_1 + X(x) + v_2 \cdot Y(x))\) at least within the domain \((0, 1, 2, 3)\).For example, letting \(v_1 = 3\) and \(v_2 = 2\), we get: X(x) 0 1 2 3 4 \(Y(x)\) -2 1 0 1 \(v_1 + X(x) + v_2 \cdot Y(x)\) -1 6 5 8 \(p(x)\) 1 -1 -6 -30 -240 Notice that (aside from the first column) every \(p(x)\) value equals the value to the left of it multiplied by the value to the left and above it. The result we care about is \(p(4) = -240\). Now, consider the case where instead of \(X(x) = x\), we set \(X(x) = \frac x^3 - 4x^2 + \fracx\) (that is, the polynomial that evaluates to \((0, 3, 2, 1)\) at the coordinates \((0, 1, 2, 3)\)). If you run the same procedure, you'll find that you also get \(p(4) = -240\). This is not a coincidence (in fact, if you randomly pick \(v_1\) and \(v_2\) from a sufficiently large field, it will almost never happen coincidentally). Rather, this happens because \(Y(1) = Y(3)\), so if you "swap the \(X\) coordinates" of the points \((1, 1)\) and \((3, 1)\) you're not changing the set of points, and because the accumulator encodes a set (as multiplication does not care about order) the value at the end will be the same.Now we can start to see the basic technique that we will use to prove copy constraints. First, consider the simple case where we only want to prove copy constraints within one set of wires (eg. we want to prove \(a(1) = a(3)\)). We'll make two coordinate accumulators: one where \(X(x) = x\) and \(Y(x) = a(x)\), and the other where \(Y(x) = a(x)\) but \(X'(x)\) is the polynomial that evaluates to the permutation that flips (or otherwise rearranges) the values in each copy constraint; in the \(a(1) = a(3)\) case this would mean the permutation would start \(0 3 2 1 4...\). The first accumulator would be compressing \(((0, a(0)), (1, a(1)), (2, a(2)), (3, a(3)), (4, a(4))...\), the second \(((0, a(0)), (3, a(1)), (2, a(2)), (1, a(3)), (4, a(4))...\). The only way the two can give the same result is if \(a(1) = a(3)\).To prove constraints between \(a\), \(b\) and \(c\), we use the same procedure, but instead "accumulate" together points from all three polynomials. We assign each of \(a\), \(b\), \(c\) a range of \(X\) coordinates (eg. \(a\) gets \(X_a(x) = x\) ie. \(0...n-1\), \(b\) gets \(X_b(x) = n+x\), ie. \(n...2n-1\), \(c\) gets \(X_c(x) = 2n+x\), ie. \(2n...3n-1\). To prove copy constraints that hop between different sets of wires, the "alternate" \(X\) coordinates would be slices of a permutation across all three sets. For example, if we want to prove \(a(2) = b(4)\) with \(n = 5\), then \(X'_a(x)\) would have evaluations \(\\) and \(X'_b(x)\) would have evaluations \(\\) (notice the \(2\) and \(9\) flipped, where \(9\) corresponds to the \(b_4\) wire). Often, \(X'_a(x)\), \(X'_b(x)\) and \(X'_c(x)\) are also called \(\sigma_a(x)\), \(\sigma_b(x)\) and \(\sigma_c(x)\).We would then instead of checking equality within one run of the procedure (ie. checking \(p(4) = p'(4)\) as before), we would check the product of the three different runs on each side:\[ p_(n) \cdot p_(n) \cdot p_(n)=p_^(n) \cdot p_^(n) \cdot p_^(n) \]The product of the three \(p(n)\) evaluations on each side accumulates all coordinate pairs in the \(a\), \(b\) and \(c\) runs on each side together, so this allows us to do the same check as before, except that we can now check copy constraints not just between positions within one of the three sets of wires \(a\), \(b\) or \(c\), but also between one set of wires and another (eg. as in \(a(2) = b(4)\)).And that's all there is to it!Putting it all togetherIn reality, all of this math is done not over integers, but over a prime field; check the section "A Modular Math Interlude" here for a description of what prime fields are. Also, for mathematical reasons perhaps best appreciated by reading and understanding this article on FFT implementation, instead of representing wire indices with \(x=0....n-1\), we'll use powers of \(\omega: 1, \omega, \omega ^2....\omega ^\) where \(\omega\) is a high-order root-of-unity in the field. This changes nothing about the math, except that the coordinate pair accumulator constraint checking equation changes from \(p(x + 1) = p(x) \cdot (v_1 + X(x) + v_2 \cdot Y(x))\) to \(p(\omega \cdot x) = p(x) \cdot (v_1 + X(x) + v_2 \cdot Y(x))\), and instead of using \(0..n-1\), \(n..2n-1\), \(2n..3n-1\) as coordinates we use \(\omega^i, g \cdot \omega^i\) and \(g^2 \cdot \omega^i\) where \(g\) can be some random high-order element in the field.Now let's write out all the equations we need to check. First, the main gate-constraint satisfaction check:\[ Q_(x) a(x)+Q_(x) b(x)+Q_(x) c(x)+Q_(x) a(x) b(x)+Q_(x)=0 \]Then the polynomial accumulator transition constraint (note: think of "\(= Z(x) \cdot H(x)\)" as meaning "equals zero for all coordinates within some particular domain that we care about, but not necessarily outside of it"):\[ \begin(\omega x)-P_(x)\left(v_+x+v_ a(x)\right) =Z(x) H_(x)} \\ }(\omega x)-P_}(x)\left(v_+\sigma_(x)+v_ a(x)\right)=Z(x) H_(x)} \\ (\omega x)-P_(x)\left(v_+g x+v_ b(x)\right)=Z(x) H_(x)} \\ }(\omega x)-P_}(x)\left(v_+\sigma_(x)+v_ b(x)\right)=Z(x) H_(x)} \\ (\omega x)-P_(x)\left(v_+g^ x+v_ c(x)\right)=Z(x) H_(x)} \\ }(\omega x)-P_}(x)\left(v_+\sigma_(x)+v_ c(x)\right)=Z(x) H_(x)}\end \]Then the polynomial accumulator starting and ending constraints:\[ \begin(1)=P_(1)=P_(1)=P_}(1)=P_}(1)=P_}(1)=1} \\ \left(\omega^\right) P_\left(\omega^\right) P_\left(\omega^\right)=P_}\left(\omega^\right) P_}\left(\omega^\right) P_}\left(\omega^\right)}\end \]The user-provided polynomials are:The wire assignments \(a(x), b(x), c(x)\) The coordinate accumulators \(P_a(x), P_b(x), P_c(x), P_(x), P_(x), P_(x)\) The quotients \(H(x)\) and \(H_1(x)...H_6(x)\) The program-specific polynomials that the prover and verifier need to compute ahead of time are:\(Q_L(x), Q_R(x), Q_O(x), Q_M(x), Q_C(x)\), which together represent the gates in the circuit (note that \(Q_C(x)\) encodes public inputs, so it may need to be computed or modified at runtime) The "permutation polynomials" \(\sigma_a(x), \sigma_b(x)\) and \(\sigma_c(x)\), which encode the copy constraints between the \(a\), \(b\) and \(c\) wires Note that the verifier need only store commitments to these polynomials. The only remaining polynomial in the above equations is \(Z(x) = (x - 1) \cdot (x - \omega) \cdot ... \cdot (x - \omega ^)\) which is designed to evaluate to zero at all those points. Fortunately, \(\omega\) can be chosen to make this polynomial very easy to evaluate: the usual technique is to choose \(\omega\) to satisfy \(\omega ^n = 1\), in which case \(Z(x) = x^n - 1\).There is one nuance here: the constraint between \(P_a(\omega^)\) and \(P_a(\omega^i)\) can't be true across the entire circle of powers of \(\omega\); it's almost always false at \(\omega^\) as the next coordinate is \(\omega^n = 1\) which brings us back to the start of the "accumulator"; to fix this, we can modify the constraint to say "either the constraint is true or \(x = \omega^\)", which one can do by multiplying \(x - \omega^\) into the constraint so it equals zero at that point.The only constraint on \(v_1\) and \(v_2\) is that the user must not be able to choose \(a(x), b(x)\) or \(c(x)\) after \(v_1\) and \(v_2\) become known, so we can satisfy this by computing \(v_1\) and \(v_2\) from hashes of commitments to \(a(x), b(x)\) and \(c(x)\).So now we've turned the program satisfaction problem into a simple problem of satisfying a few equations with polynomials, and there are some optimizations in PLONK that allow us to remove many of the polynomials in the above equations that I will not go into to preserve simplicity. But the polynomials themselves, both the program-specific parameters and the user inputs, are big. So the next question is, how do we get around this so we can make the proof short?Polynomial commitmentsA polynomial commitment is a short object that "represents" a polynomial, and allows you to verify evaluations of that polynomial, without needing to actually contain all of the data in the polynomial. That is, if someone gives you a commitment \(c\) representing \(P(x)\), they can give you a proof that can convince you, for some specific \(z\), what the value of \(P(z)\) is. There is a further mathematical result that says that, over a sufficiently big field, if certain kinds of equations (chosen before \(z\) is known) about polynomials evaluated at a random \(z\) are true, those same equations are true about the whole polynomial as well. For example, if \(P(z) \cdot Q(z) + R(z) = S(z) + 5\), then we know that it's overwhelmingly likely that \(P(x) \cdot Q(x) + R(x) = S(x) + 5\) in general. Using such polynomial commitments, we could very easily check all of the above polynomial equations above - make the commitments, use them as input to generate \(z\), prove what the evaluations are of each polynomial at \(z\), and then run the equations with these evaluations instead of the original polynomials. But how do these commitments work?There are two parts: the commitment to the polynomial \(P(x) \rightarrow c\), and the opening to a value \(P(z)\) at some \(z\). To make a commitment, there are many techniques; one example is FRI, and another is Kate commitments which I will describe below. To prove an opening, it turns out that there is a simple generic "subtract-and-divide" trick: to prove that \(P(z) = a\), you prove that\[ \frac \]is also a polynomial (using another polynomial commitment). This works because if the quotient is a polynomial (ie. it is not fractional), then \(x - z\) is a factor of \(P(x) - a\), so \((P(x) - a)(z) = 0\), so \(P(z) = a\). Try it with some polynomial, eg. \(P(x) = x^3 + 2 \cdot x^2 + 5\) with \((z = 6, a = 293)\), yourself; and try \((z = 6, a = 292)\) and see how it fails (if you're lazy, see WolframAlpha here vs here). Note also a generic optimization: to prove many openings of many polynomials at the same time, after committing to the outputs do the subtract-and-divide trick on a random linear combination of the polynomials and the outputs.So how do the commitments themselves work? Kate commitments are, fortunately, much simpler than FRI. A trusted-setup procedure generates a set of elliptic curve points \(G, G \cdot s, G \cdot s^2\) .... \(G \cdot s^n\), as well as \(G_2 \cdot s\), where \(G\) and \(G_2\) are the generators of two elliptic curve groups and \(s\) is a secret that is forgotten once the procedure is finished (note that there is a multi-party version of this setup, which is secure as long as at least one of the participants forgets their share of the secret). These points are published and considered to be "the proving key" of the scheme; anyone who needs to make a polynomial commitment will need to use these points. A commitment to a degree-d polynomial is made by multiplying each of the first d+1 points in the proving key by the corresponding coefficient in the polynomial, and adding the results together.Notice that this provides an "evaluation" of that polynomial at \(s\), without knowing \(s\). For example, \(x^3 + 2x^2+5\) would be represented by \((G \cdot s^3) + 2 \cdot (G \cdot s^2) + 5 \cdot G\). We can use the notation \([P]\) to refer to \(P\) encoded in this way (ie. \(G \cdot P(s)\)). When doing the subtract-and-divide trick, you can prove that the two polynomials actually satisfy the relation by using elliptic curve pairings: check that \(e([P] - G \cdot a, G_2) = e([Q], [x] - G_2 \cdot z)\) as a proxy for checking that \(P(x) - a = Q(x) \cdot (x - z)\).But there are more recently other types of polynomial commitments coming out too. A new scheme called DARK ("Diophantine arguments of knowledge") uses "hidden order groups" such as class groups to implement another kind of polynomial commitment. Hidden order groups are unique because they allow you to compress arbitrarily large numbers into group elements, even numbers much larger than the size of the group element, in a way that can't be "spoofed"; constructions from VDFs to accumulators to range proofs to polynomial commitments can be built on top of this. Another option is to use bulletproofs, using regular elliptic curve groups at the cost of the proof taking much longer to verify. Because polynomial commitments are much simpler than full-on zero knowledge proof schemes, we can expect more such schemes to get created in the future.RecapTo finish off, let's go over the scheme again. Given a program \(P\), you convert it into a circuit, and generate a set of equations that look like this:\[ \left(Q_}\right) a_+\left(Q_}\right) b_+\left(Q_}\right) c_+\left(Q_}\right) a_ b_+Q_}=0 \]You then convert this set of equations into a single polynomial equation:\[ Q_(x) a(x)+Q_(x) b(x)+Q_(x) c(x)+Q_(x) a(x) b(x)+Q_(x)=0 \]You also generate from the circuit a list of copy constraints. From these copy constraints you generate the three polynomials representing the permuted wire indices: \(\sigma_a(x), \sigma_b(x), \sigma_c(x)\). To generate a proof, you compute the values of all the wires and convert them into three polynomials: \(a(x), b(x), c(x)\). You also compute six "coordinate pair accumulator" polynomials as part of the permutation-check argument. Finally you compute the cofactors \(H_i(x)\).There is a set of equations between the polynomials that need to be checked; you can do this by making commitments to the polynomials, opening them at some random \(z\) (along with proofs that the openings are correct), and running the equations on these evaluations instead of the original polynomials. The proof itself is just a few commitments and openings and can be checked with a few equations. And that's all there is to it! -
 The Dawn of Hybrid Layer 2 Protocols The Dawn of Hybrid Layer 2 Protocols2019 Aug 28 See all posts The Dawn of Hybrid Layer 2 Protocols Special thanks to the Plasma Group team for review and feedbackCurrent approaches to layer 2 scaling - basically, Plasma and state channels - are increasingly moving from theory to practice, but at the same time it is becoming easier to see the inherent challenges in treating these techniques as a fully fledged scaling solution for Ethereum. Ethereum was arguably successful in large part because of its very easy developer experience: you write a program, publish the program, and anyone can interact with it. Designing a state channel or Plasma application, on the other hand, relies on a lot of explicit reasoning about incentives and application-specific development complexity. State channels work well for specific use cases such as repeated payments between the same two parties and two-player games (as successfully implemented in Celer), but more generalized usage is proving challenging. Plasma, particularly Plasma Cash, can work well for payments, but generalization similarly incurs challenges: even implementing a decentralized exchange requires clients to store much more history data, and generalizing to Ethereum-style smart contracts on Plasma seems extremely difficult.But at the same time, there is a resurgence of a forgotten category of "semi-layer-2" protocols - a category which promises less extreme gains in scaling, but with the benefit of much easier generalization and more favorable security models. A long-forgotten blog post from 2014 introduced the idea of "shadow chains", an architecture where block data is published on-chain, but blocks are not verified by default. Rather, blocks are tentatively accepted, and only finalized after some period of time (eg. 2 weeks). During those 2 weeks, a tentatively accepted block can be challenged; only then is the block verified, and if the block proves to be invalid then the chain from that block on is reverted, and the original publisher's deposit is penalized. The contract does not keep track of the full state of the system; it only keeps track of the state root, and users themselves can calculate the state by processing the data submitted to the chain from start to head. A more recent proposal, ZK Rollup, does the same thing without challenge periods, by using ZK-SNARKs to verify blocks' validity. Anatomy of a ZK Rollup package that is published on-chain. Hundreds of "internal transactions" that affect the state (ie. account balances) of the ZK Rollup system are compressed into a package that contains ~10 bytes per internal transaction that specifies the state transitions, plus a ~100-300 byte SNARK proving that the transitions are all valid. In both cases, the main chain is used to verify data availability, but does not (directly) verify block validity or perform any significant computation, unless challenges are made. This technique is thus not a jaw-droppingly huge scalability gain, because the on-chain data overhead eventually presents a bottleneck, but it is nevertheless a very significant one. Data is cheaper than computation, and there are ways to compress transaction data very significantly, particularly because the great majority of data in a transaction is the signature and many signatures can be compressed into one through many forms of aggregation. ZK Rollup promises 500 tx/sec, a 30x gain over the Ethereum chain itself, by compressing each transaction to a mere ~10 bytes; signatures do not need to be included because their validity is verified by the zero-knowledge proof. With BLS aggregate signatures a similar throughput can be achieved in shadow chains (more recently called "optimistic rollup" to highlight its similarities to ZK Rollup). The upcoming Istanbul hard fork will reduce the gas cost of data from 68 per byte to 16 per byte, increasing the throughput of these techniques by another 4x (that's over 2000 transactions per second).So what is the benefit of data on-chain techniques such as ZK/optimistic rollup versus data off-chain techniques such as Plasma? First of all, there is no need for semi-trusted operators. In ZK Rollup, because validity is verified by cryptographic proofs there is literally no way for a package submitter to be malicious (depending on the setup, a malicious submitter may cause the system to halt for a few seconds, but this is the most harm that can be done). In optimistic rollup, a malicious submitter can publish a bad block, but the next submitter will immediately challenge that block before publishing their own. In both ZK and optimistic rollup, enough data is published on chain to allow anyone to compute the complete internal state, simply by processing all of the submitted deltas in order, and there is no "data withholding attack" that can take this property away. Hence, becoming an operator can be fully permissionless; all that is needed is a security deposit (eg. 10 ETH) for anti-spam purposes.Second, optimistic rollup particularly is vastly easier to generalize; the state transition function in an optimistic rollup system can be literally anything that can be computed within the gas limit of a single block (including the Merkle branches providing the parts of the state needed to verify the transition). ZK Rollup is theoretically generalizeable in the same way, though in practice making ZK SNARKs over general-purpose computation (such as EVM execution) is very difficult, at least for now. Third, optimistic rollup is much easier to build clients for, as there is less need for second-layer networking infrastructure; more can be done by just scanning the blockchain.But where do these advantages come from? The answer lies in a highly technical issue known as the data availability problem (see note, video). Basically, there are two ways to try to cheat in a layer-2 system. The first is to publish invalid data to the blockchain. The second is to not publish data at all (eg. in Plasma, publishing the root hash of a new Plasma block to the main chain but without revealing the contents of the block to anyone). Published-but-invalid data is very easy to deal with, because once the data is published on-chain there are multiple ways to figure out unambiguously whether or not it's valid, and an invalid submission is unambiguously invalid so the submitter can be heavily penalized. Unavailable data, on the other hand, is much harder to deal with, because even though unavailability can be detected if challenged, one cannot reliably determine whose fault the non-publication is, especially if data is withheld by default and revealed on-demand only when some verification mechanism tries to verify its availability. This is illustrated in the "Fisherman's dilemma", which shows how a challenge-response game cannot distinguish between malicious submitters and malicious challengers: Fisherman's dilemma. If you only start watching the given specific piece of data at time T3, you have no idea whether you are living in Case 1 or Case 2, and hence who is at fault.Plasma and channels both work around the fisherman's dilemma by pushing the problem to users: if you as a user decide that another user you are interacting with (a counterparty in a state channel, an operator in a Plasma chain) is not publishing data to you that they should be publishing, it's your responsibility to exit and move to a different counterparty/operator. The fact that you as a user have all of the previous data, and data about all of the transactions you signed, allows you to prove to the chain what assets you held inside the layer-2 protocol, and thus safely bring them out of the system. You prove the existence of a (previously agreed) operation that gave the asset to you, no one else can prove the existence of an operation approved by you that sent the asset to someone else, so you get the asset.The technique is very elegant. However, it relies on a key assumption: that every state object has a logical "owner", and the state of the object cannot be changed without the owner's consent. This works well for UTXO-based payments (but not account-based payments, where you can edit someone else's balance upward without their consent; this is why account-based Plasma is so hard), and it can even be made to work for a decentralized exchange, but this "ownership" property is far from universal. Some applications, eg. Uniswap don't have a natural owner, and even in those applications that do, there are often multiple people that can legitimately make edits to the object. And there is no way to allow arbitrary third parties to exit an asset without introducing the possibility of denial-of-service (DoS) attacks, precisely because one cannot prove whether the publisher or submitter is at fault.There are other issues peculiar to Plasma and channels individually. Channels do not allow off-chain transactions to users that are not already part of the channel (argument: suppose there existed a way to send $1 to an arbitrary new user from inside a channel. Then this technique could be used many times in parallel to send $1 to more users than there are funds in the system, already breaking its security guarantee). Plasma requires users to store large amounts of history data, which gets even bigger when different assets can be intertwined (eg. when an asset is transferred conditional on transfer of another asset, as happens in a decentralized exchange with a single-stage order book mechanism).Because data-on-chain computation-off-chain layer 2 techniques don't have data availability issues, they have none of these weaknesses. ZK and optimistic rollup take great care to put enough data on chain to allow users to calculate the full state of the layer 2 system, ensuring that if any participant disappears a new one can trivially take their place. The only issue that they have is verifying computation without doing the computation on-chain, which is a much easier problem. And the scalability gains are significant: ~10 bytes per transaction in ZK Rollup, and a similar level of scalability can be achieved in optimistic rollup by using BLS aggregation to aggregate signatures. This corresponds to a theoretical maximum of ~500 transactions per second today, and over 2000 post-Istanbul.But what if you want more scalability? Then there is a large middle ground between data-on-chain layer 2 and data-off-chain layer 2 protocols, with many hybrid approaches that give you some of the benefits of both. To give a simple example, the history storage blowup in a decentralized exchange implemented on Plasma Cash can be prevented by publishing a mapping of which orders are matched with which orders (that's less than 4 bytes per order) on chain: Left: History data a Plasma Cash user needs to store if they own 1 coin. Middle: History data a Plasma Cash user needs to store if they own 1 coin that was exchanged with another coin using an atomic swap. Right: History data a Plasma Cash user needs to store if the order matching is published on chain. Even outside of the decentralized exchange context, the amount of history that users need to store in Plasma can be reduced by having the Plasma chain periodically publish some per-user data on-chain. One could also imagine a platform which works like Plasma in the case where some state does have a logical "owner" and works like ZK or optimistic rollup in the case where it does not. Plasma developers are already starting to work on these kinds of optimizations.There is thus a strong case to be made for developers of layer 2 scalability solutions to move to be more willing to publish per-user data on-chain at least some of the time: it greatly increases ease of development, generality and security and reduces per-user load (eg. no need for users storing history data). The efficiency losses of doing so are also overstated: even in a fully off-chain layer-2 architecture, users depositing, withdrawing and moving between different counterparties and providers is going to be an inevitable and frequent occurrence, and so there will be a significant amount of per-user on-chain data regardless. The hybrid route opens the door to a relatively fast deployment of fully generalized Ethereum-style smart contracts inside a quasi-layer-2 architecture.See also:Introducing the OVM Blog post by Karl Floersch Related ideas by John Adler
The Dawn of Hybrid Layer 2 Protocols The Dawn of Hybrid Layer 2 Protocols2019 Aug 28 See all posts The Dawn of Hybrid Layer 2 Protocols Special thanks to the Plasma Group team for review and feedbackCurrent approaches to layer 2 scaling - basically, Plasma and state channels - are increasingly moving from theory to practice, but at the same time it is becoming easier to see the inherent challenges in treating these techniques as a fully fledged scaling solution for Ethereum. Ethereum was arguably successful in large part because of its very easy developer experience: you write a program, publish the program, and anyone can interact with it. Designing a state channel or Plasma application, on the other hand, relies on a lot of explicit reasoning about incentives and application-specific development complexity. State channels work well for specific use cases such as repeated payments between the same two parties and two-player games (as successfully implemented in Celer), but more generalized usage is proving challenging. Plasma, particularly Plasma Cash, can work well for payments, but generalization similarly incurs challenges: even implementing a decentralized exchange requires clients to store much more history data, and generalizing to Ethereum-style smart contracts on Plasma seems extremely difficult.But at the same time, there is a resurgence of a forgotten category of "semi-layer-2" protocols - a category which promises less extreme gains in scaling, but with the benefit of much easier generalization and more favorable security models. A long-forgotten blog post from 2014 introduced the idea of "shadow chains", an architecture where block data is published on-chain, but blocks are not verified by default. Rather, blocks are tentatively accepted, and only finalized after some period of time (eg. 2 weeks). During those 2 weeks, a tentatively accepted block can be challenged; only then is the block verified, and if the block proves to be invalid then the chain from that block on is reverted, and the original publisher's deposit is penalized. The contract does not keep track of the full state of the system; it only keeps track of the state root, and users themselves can calculate the state by processing the data submitted to the chain from start to head. A more recent proposal, ZK Rollup, does the same thing without challenge periods, by using ZK-SNARKs to verify blocks' validity. Anatomy of a ZK Rollup package that is published on-chain. Hundreds of "internal transactions" that affect the state (ie. account balances) of the ZK Rollup system are compressed into a package that contains ~10 bytes per internal transaction that specifies the state transitions, plus a ~100-300 byte SNARK proving that the transitions are all valid. In both cases, the main chain is used to verify data availability, but does not (directly) verify block validity or perform any significant computation, unless challenges are made. This technique is thus not a jaw-droppingly huge scalability gain, because the on-chain data overhead eventually presents a bottleneck, but it is nevertheless a very significant one. Data is cheaper than computation, and there are ways to compress transaction data very significantly, particularly because the great majority of data in a transaction is the signature and many signatures can be compressed into one through many forms of aggregation. ZK Rollup promises 500 tx/sec, a 30x gain over the Ethereum chain itself, by compressing each transaction to a mere ~10 bytes; signatures do not need to be included because their validity is verified by the zero-knowledge proof. With BLS aggregate signatures a similar throughput can be achieved in shadow chains (more recently called "optimistic rollup" to highlight its similarities to ZK Rollup). The upcoming Istanbul hard fork will reduce the gas cost of data from 68 per byte to 16 per byte, increasing the throughput of these techniques by another 4x (that's over 2000 transactions per second).So what is the benefit of data on-chain techniques such as ZK/optimistic rollup versus data off-chain techniques such as Plasma? First of all, there is no need for semi-trusted operators. In ZK Rollup, because validity is verified by cryptographic proofs there is literally no way for a package submitter to be malicious (depending on the setup, a malicious submitter may cause the system to halt for a few seconds, but this is the most harm that can be done). In optimistic rollup, a malicious submitter can publish a bad block, but the next submitter will immediately challenge that block before publishing their own. In both ZK and optimistic rollup, enough data is published on chain to allow anyone to compute the complete internal state, simply by processing all of the submitted deltas in order, and there is no "data withholding attack" that can take this property away. Hence, becoming an operator can be fully permissionless; all that is needed is a security deposit (eg. 10 ETH) for anti-spam purposes.Second, optimistic rollup particularly is vastly easier to generalize; the state transition function in an optimistic rollup system can be literally anything that can be computed within the gas limit of a single block (including the Merkle branches providing the parts of the state needed to verify the transition). ZK Rollup is theoretically generalizeable in the same way, though in practice making ZK SNARKs over general-purpose computation (such as EVM execution) is very difficult, at least for now. Third, optimistic rollup is much easier to build clients for, as there is less need for second-layer networking infrastructure; more can be done by just scanning the blockchain.But where do these advantages come from? The answer lies in a highly technical issue known as the data availability problem (see note, video). Basically, there are two ways to try to cheat in a layer-2 system. The first is to publish invalid data to the blockchain. The second is to not publish data at all (eg. in Plasma, publishing the root hash of a new Plasma block to the main chain but without revealing the contents of the block to anyone). Published-but-invalid data is very easy to deal with, because once the data is published on-chain there are multiple ways to figure out unambiguously whether or not it's valid, and an invalid submission is unambiguously invalid so the submitter can be heavily penalized. Unavailable data, on the other hand, is much harder to deal with, because even though unavailability can be detected if challenged, one cannot reliably determine whose fault the non-publication is, especially if data is withheld by default and revealed on-demand only when some verification mechanism tries to verify its availability. This is illustrated in the "Fisherman's dilemma", which shows how a challenge-response game cannot distinguish between malicious submitters and malicious challengers: Fisherman's dilemma. If you only start watching the given specific piece of data at time T3, you have no idea whether you are living in Case 1 or Case 2, and hence who is at fault.Plasma and channels both work around the fisherman's dilemma by pushing the problem to users: if you as a user decide that another user you are interacting with (a counterparty in a state channel, an operator in a Plasma chain) is not publishing data to you that they should be publishing, it's your responsibility to exit and move to a different counterparty/operator. The fact that you as a user have all of the previous data, and data about all of the transactions you signed, allows you to prove to the chain what assets you held inside the layer-2 protocol, and thus safely bring them out of the system. You prove the existence of a (previously agreed) operation that gave the asset to you, no one else can prove the existence of an operation approved by you that sent the asset to someone else, so you get the asset.The technique is very elegant. However, it relies on a key assumption: that every state object has a logical "owner", and the state of the object cannot be changed without the owner's consent. This works well for UTXO-based payments (but not account-based payments, where you can edit someone else's balance upward without their consent; this is why account-based Plasma is so hard), and it can even be made to work for a decentralized exchange, but this "ownership" property is far from universal. Some applications, eg. Uniswap don't have a natural owner, and even in those applications that do, there are often multiple people that can legitimately make edits to the object. And there is no way to allow arbitrary third parties to exit an asset without introducing the possibility of denial-of-service (DoS) attacks, precisely because one cannot prove whether the publisher or submitter is at fault.There are other issues peculiar to Plasma and channels individually. Channels do not allow off-chain transactions to users that are not already part of the channel (argument: suppose there existed a way to send $1 to an arbitrary new user from inside a channel. Then this technique could be used many times in parallel to send $1 to more users than there are funds in the system, already breaking its security guarantee). Plasma requires users to store large amounts of history data, which gets even bigger when different assets can be intertwined (eg. when an asset is transferred conditional on transfer of another asset, as happens in a decentralized exchange with a single-stage order book mechanism).Because data-on-chain computation-off-chain layer 2 techniques don't have data availability issues, they have none of these weaknesses. ZK and optimistic rollup take great care to put enough data on chain to allow users to calculate the full state of the layer 2 system, ensuring that if any participant disappears a new one can trivially take their place. The only issue that they have is verifying computation without doing the computation on-chain, which is a much easier problem. And the scalability gains are significant: ~10 bytes per transaction in ZK Rollup, and a similar level of scalability can be achieved in optimistic rollup by using BLS aggregation to aggregate signatures. This corresponds to a theoretical maximum of ~500 transactions per second today, and over 2000 post-Istanbul.But what if you want more scalability? Then there is a large middle ground between data-on-chain layer 2 and data-off-chain layer 2 protocols, with many hybrid approaches that give you some of the benefits of both. To give a simple example, the history storage blowup in a decentralized exchange implemented on Plasma Cash can be prevented by publishing a mapping of which orders are matched with which orders (that's less than 4 bytes per order) on chain: Left: History data a Plasma Cash user needs to store if they own 1 coin. Middle: History data a Plasma Cash user needs to store if they own 1 coin that was exchanged with another coin using an atomic swap. Right: History data a Plasma Cash user needs to store if the order matching is published on chain. Even outside of the decentralized exchange context, the amount of history that users need to store in Plasma can be reduced by having the Plasma chain periodically publish some per-user data on-chain. One could also imagine a platform which works like Plasma in the case where some state does have a logical "owner" and works like ZK or optimistic rollup in the case where it does not. Plasma developers are already starting to work on these kinds of optimizations.There is thus a strong case to be made for developers of layer 2 scalability solutions to move to be more willing to publish per-user data on-chain at least some of the time: it greatly increases ease of development, generality and security and reduces per-user load (eg. no need for users storing history data). The efficiency losses of doing so are also overstated: even in a fully off-chain layer-2 architecture, users depositing, withdrawing and moving between different counterparties and providers is going to be an inevitable and frequent occurrence, and so there will be a significant amount of per-user on-chain data regardless. The hybrid route opens the door to a relatively fast deployment of fully generalized Ethereum-style smart contracts inside a quasi-layer-2 architecture.See also:Introducing the OVM Blog post by Karl Floersch Related ideas by John Adler -
 Sidechains vs Plasma vs Sharding Sidechains vs Plasma vs Sharding2019 Jun 12 See all posts Sidechains vs Plasma vs Sharding Special thanks to Jinglan Wang for review and feedbackOne question that often comes up is: how exactly is sharding different from sidechains or Plasma? All three architectures seem to involve a hub-and-spoke architecture with a central "main chain" that serves as the consensus backbone of the system, and a set of "child" chains containing actual user-level transactions. Hashes from the child chains are usually periodically published into the main chain (sharded chains with no hub are theoretically possible but haven't been done so far; this article will not focus on them, but the arguments are similar). Given this fundamental similarity, why go with one approach over the others?Distinguishing sidechains from Plasma is simple. Plasma chains are sidechains that have a non-custodial property: if there is any error in the Plasma chain, then the error can be detected, and users can safely exit the Plasma chain and prevent the attacker from doing any lasting damage. The only cost that users suffer is that they must wait for a challenge period and pay some higher transaction fees on the (non-scalable) base chain. Regular sidechains do not have this safety property, so they are less secure. However, designing Plasma chains is in many cases much harder, and one could argue that for many low-value applications the security is not worth the added complexity.So what about Plasma versus sharding? The key technical difference has to do with the notion of tight coupling. Tight coupling is a property of sharding, but NOT a property of sidechains or Plasma, that says that the validity of the main chain ("beacon chain" in ethereum 2.0) is inseparable from the validity of the child chains. That is, a child chain block that specifies an invalid main chain block as a dependency is by definition invalid, and more importantly a main chain block that includes an invalid child chain block is by definition invalid.In non-sharded blockchains, this idea that the canonical chain (ie. the chain that everyone accepts as representing the "real" history) is by definition fully available and valid also applies; for example in the case of Bitcoin and Ethereum one typically says that the canonical chain is the "longest valid chain" (or, more pedantically, the "heaviest valid and available chain"). In sharded blockchains, this idea that the canonical chain is the heaviest valid and available chain by definition also applies, with the validity and availability requirement applying to both the main chain and shard chains. The new challenge that a sharded system has, however, is that users have no way of fully verifying the validity and availability of any given chain directly, because there is too much data. The challenge of engineering sharded chains is to get around this limitation by giving users a maximally trustless and practical indirect means to verify which chains are fully available and valid, so that they can still determine which chain is canonical. In practice, this includes techniques like committees, SNARKs/STARKs, fisherman schemes and fraud and data availability proofs.If a chain structure does not have this tight-coupling property, then it is arguably not a layer-1 sharding scheme, but rather a layer-2 system sitting on top of a non-scalable layer-1 chain. Plasma is not a tightly-coupled system: an invalid Plasma block absolutely can have its header be committed into the main Ethereum chain, because the Ethereum base layer has no idea that it represents an invalid Plasma block, or even that it represents a Plasma block at all; all that it sees is a transaction containing a small piece of data. However, the consequences of a single Plasma chain failing are localized to within that Plasma chain. Sharding Try really hard to ensure total validity/availability of every part of the system Plasma Accept local faults but try to limit their consequences However, if you try to analyze the process of how users perform the "indirect validation" procedure to determine if the chain they are looking at is fully valid and available without downloading and executing the whole thing, one can find more similarities with how Plasma works. For example, a common technique used to prevent availability issues is fishermen: if a node sees a given piece of a block as unavailable, it can publish a challenge claiming this, creating a time period within which anyone can publish that piece of data. If a block goes unchallenged for long enough, the blocks and all blocks that cite it as a dependency can be reverted. This seems fundamentally similar to Plasma, where if a block is unavailable users can publish a message to the main chain to exit their state in response. Both techniques eventually buckle under pressure in the same way: if there are too many false challenges in a sharded system, then users cannot keep track of whether or not all of the availability challenges have been answered, and if there are too many availability challenges in a Plasma system then the main chain could get overwhelmed as the exits fill up the chain's block size limit. In both cases, it seems like there's a system that has nominally \(O(C^2)\) scalability (where \(C\) is the computing power of one node) but where scalability falls to \(O(C)\) in the event of an attack. However, sharding has more defenses against this.First of all, modern sharded designs use randomly sampled committees, so one cannot easily dominate even one committee enough to produce a fake block unless one has a large portion (perhaps \(>\frac\)) of the entire validator set of the chain. Second, there are better strategies to handling data availability than fishermen: data availability proofs. In a scheme using data availability proofs, if a block is unavailable, then clients' data availability checks will fail and clients will see that block as unavailable. If the block is invalid, then even a single fraud proof will convince them of this fact for an entire block. An \(O(1)\)-sized fraud proof can convince a client of the invalidity of an \(O(C)\)-sized block, and so \(O(C)\) data suffices to convince a client of the invalidity of \(O(C^2)\) data (this is in the worst case where the client is dealing with \(N\) sister blocks all with the same parent of which only one is valid; in more likely cases, one single fraud proof suffices to prove invalidity of an entire invalid chain). Hence, sharded systems are theoretically less vulnerable to being overwhelmed by denial-of-service attacks than Plasma chains.Second, sharded chains provide stronger guarantees in the face of large and majority attackers (with more than \(\frac\) or even \(\frac\) of the validator set). A Plasma chain can always be successfully attacked by a 51% attack on the main chain that censors exits; a sharded chain cannot. This is because data availability proofs and fraud proofs happen inside the client, rather than inside the chain, so they cannot be censored by 51% attacks. Third, the defenses provided by sharded chains are easier to generalize; Plasma's model of exits requires state to be separated into discrete pieces each of which is in the interest of any single actor to maintain, whereas sharded chains relying on data availability proofs, fraud proofs, fishermen and random sampling are theoretically universal.So there really is a large difference between validity and availability guarantees that are provided at layer 2, which are limited and more complex as they require explicit reasoning about incentives and which party has an interest in which pieces of state, and guarantees that are provided by a layer 1 system that is committed to fully satisfying them.But Plasma chains also have large advantages too. First, they can be iterated and new designs can be implemented more quickly, as each Plasma chain can be deployed separately without coordinating the rest of the ecosystem. Second, sharding is inherently more fragile, as it attempts to guarantee absolute and total availability and validity of some quantity of data, and this quantity must be set in the protocol; too little, and the system has less scalability than it could have had, too much, and the entire system risks breaking. The maximum safe level of scalability also depends on the number of users of the system, which is an unpredictable variable. Plasma chains, on the other hand, allow different users to make different tradeoffs in this regard, and allow users to adjust more flexibly to changes in circumstances.Single-operator Plasma chains can also be used to offer more privacy than sharded systems, where all data is public. Even where privacy is not desired, they are potentially more efficient, because the total data availability requirement of sharded systems requires a large extra level of redundancy as a safety margin. In Plasma systems, on the other hand, data requirements for each piece of data can be minimized, to the point where in the long term each individual piece of data may only need to be replicated a few times, rather than a thousand times as is the case in sharded systems.Hence, in the long term, a hybrid system where a sharded base layer exists, and Plasma chains exist on top of it to provide further scalability, seems like the most likely approach, more able to serve different groups' of users need than sole reliance on one strategy or the other. And it is unfortunately not the case that at a sufficient level of advancement Plasma and sharding collapse into the same design; the two are in some key ways irreducibly different (eg. the data availability checks made by clients in sharded systems cannot be moved to the main chain in Plasma because these checks only work if they are done subjectively and based on private information). But both scalability solutions (as well as state channels!) have a bright future ahead of them.
Sidechains vs Plasma vs Sharding Sidechains vs Plasma vs Sharding2019 Jun 12 See all posts Sidechains vs Plasma vs Sharding Special thanks to Jinglan Wang for review and feedbackOne question that often comes up is: how exactly is sharding different from sidechains or Plasma? All three architectures seem to involve a hub-and-spoke architecture with a central "main chain" that serves as the consensus backbone of the system, and a set of "child" chains containing actual user-level transactions. Hashes from the child chains are usually periodically published into the main chain (sharded chains with no hub are theoretically possible but haven't been done so far; this article will not focus on them, but the arguments are similar). Given this fundamental similarity, why go with one approach over the others?Distinguishing sidechains from Plasma is simple. Plasma chains are sidechains that have a non-custodial property: if there is any error in the Plasma chain, then the error can be detected, and users can safely exit the Plasma chain and prevent the attacker from doing any lasting damage. The only cost that users suffer is that they must wait for a challenge period and pay some higher transaction fees on the (non-scalable) base chain. Regular sidechains do not have this safety property, so they are less secure. However, designing Plasma chains is in many cases much harder, and one could argue that for many low-value applications the security is not worth the added complexity.So what about Plasma versus sharding? The key technical difference has to do with the notion of tight coupling. Tight coupling is a property of sharding, but NOT a property of sidechains or Plasma, that says that the validity of the main chain ("beacon chain" in ethereum 2.0) is inseparable from the validity of the child chains. That is, a child chain block that specifies an invalid main chain block as a dependency is by definition invalid, and more importantly a main chain block that includes an invalid child chain block is by definition invalid.In non-sharded blockchains, this idea that the canonical chain (ie. the chain that everyone accepts as representing the "real" history) is by definition fully available and valid also applies; for example in the case of Bitcoin and Ethereum one typically says that the canonical chain is the "longest valid chain" (or, more pedantically, the "heaviest valid and available chain"). In sharded blockchains, this idea that the canonical chain is the heaviest valid and available chain by definition also applies, with the validity and availability requirement applying to both the main chain and shard chains. The new challenge that a sharded system has, however, is that users have no way of fully verifying the validity and availability of any given chain directly, because there is too much data. The challenge of engineering sharded chains is to get around this limitation by giving users a maximally trustless and practical indirect means to verify which chains are fully available and valid, so that they can still determine which chain is canonical. In practice, this includes techniques like committees, SNARKs/STARKs, fisherman schemes and fraud and data availability proofs.If a chain structure does not have this tight-coupling property, then it is arguably not a layer-1 sharding scheme, but rather a layer-2 system sitting on top of a non-scalable layer-1 chain. Plasma is not a tightly-coupled system: an invalid Plasma block absolutely can have its header be committed into the main Ethereum chain, because the Ethereum base layer has no idea that it represents an invalid Plasma block, or even that it represents a Plasma block at all; all that it sees is a transaction containing a small piece of data. However, the consequences of a single Plasma chain failing are localized to within that Plasma chain. Sharding Try really hard to ensure total validity/availability of every part of the system Plasma Accept local faults but try to limit their consequences However, if you try to analyze the process of how users perform the "indirect validation" procedure to determine if the chain they are looking at is fully valid and available without downloading and executing the whole thing, one can find more similarities with how Plasma works. For example, a common technique used to prevent availability issues is fishermen: if a node sees a given piece of a block as unavailable, it can publish a challenge claiming this, creating a time period within which anyone can publish that piece of data. If a block goes unchallenged for long enough, the blocks and all blocks that cite it as a dependency can be reverted. This seems fundamentally similar to Plasma, where if a block is unavailable users can publish a message to the main chain to exit their state in response. Both techniques eventually buckle under pressure in the same way: if there are too many false challenges in a sharded system, then users cannot keep track of whether or not all of the availability challenges have been answered, and if there are too many availability challenges in a Plasma system then the main chain could get overwhelmed as the exits fill up the chain's block size limit. In both cases, it seems like there's a system that has nominally \(O(C^2)\) scalability (where \(C\) is the computing power of one node) but where scalability falls to \(O(C)\) in the event of an attack. However, sharding has more defenses against this.First of all, modern sharded designs use randomly sampled committees, so one cannot easily dominate even one committee enough to produce a fake block unless one has a large portion (perhaps \(>\frac\)) of the entire validator set of the chain. Second, there are better strategies to handling data availability than fishermen: data availability proofs. In a scheme using data availability proofs, if a block is unavailable, then clients' data availability checks will fail and clients will see that block as unavailable. If the block is invalid, then even a single fraud proof will convince them of this fact for an entire block. An \(O(1)\)-sized fraud proof can convince a client of the invalidity of an \(O(C)\)-sized block, and so \(O(C)\) data suffices to convince a client of the invalidity of \(O(C^2)\) data (this is in the worst case where the client is dealing with \(N\) sister blocks all with the same parent of which only one is valid; in more likely cases, one single fraud proof suffices to prove invalidity of an entire invalid chain). Hence, sharded systems are theoretically less vulnerable to being overwhelmed by denial-of-service attacks than Plasma chains.Second, sharded chains provide stronger guarantees in the face of large and majority attackers (with more than \(\frac\) or even \(\frac\) of the validator set). A Plasma chain can always be successfully attacked by a 51% attack on the main chain that censors exits; a sharded chain cannot. This is because data availability proofs and fraud proofs happen inside the client, rather than inside the chain, so they cannot be censored by 51% attacks. Third, the defenses provided by sharded chains are easier to generalize; Plasma's model of exits requires state to be separated into discrete pieces each of which is in the interest of any single actor to maintain, whereas sharded chains relying on data availability proofs, fraud proofs, fishermen and random sampling are theoretically universal.So there really is a large difference between validity and availability guarantees that are provided at layer 2, which are limited and more complex as they require explicit reasoning about incentives and which party has an interest in which pieces of state, and guarantees that are provided by a layer 1 system that is committed to fully satisfying them.But Plasma chains also have large advantages too. First, they can be iterated and new designs can be implemented more quickly, as each Plasma chain can be deployed separately without coordinating the rest of the ecosystem. Second, sharding is inherently more fragile, as it attempts to guarantee absolute and total availability and validity of some quantity of data, and this quantity must be set in the protocol; too little, and the system has less scalability than it could have had, too much, and the entire system risks breaking. The maximum safe level of scalability also depends on the number of users of the system, which is an unpredictable variable. Plasma chains, on the other hand, allow different users to make different tradeoffs in this regard, and allow users to adjust more flexibly to changes in circumstances.Single-operator Plasma chains can also be used to offer more privacy than sharded systems, where all data is public. Even where privacy is not desired, they are potentially more efficient, because the total data availability requirement of sharded systems requires a large extra level of redundancy as a safety margin. In Plasma systems, on the other hand, data requirements for each piece of data can be minimized, to the point where in the long term each individual piece of data may only need to be replicated a few times, rather than a thousand times as is the case in sharded systems.Hence, in the long term, a hybrid system where a sharded base layer exists, and Plasma chains exist on top of it to provide further scalability, seems like the most likely approach, more able to serve different groups' of users need than sole reliance on one strategy or the other. And it is unfortunately not the case that at a sufficient level of advancement Plasma and sharding collapse into the same design; the two are in some key ways irreducibly different (eg. the data availability checks made by clients in sharded systems cannot be moved to the main chain in Plasma because these checks only work if they are done subjectively and based on private information). But both scalability solutions (as well as state channels!) have a bright future ahead of them. -
 Fast Fourier Transforms Fast Fourier Transforms2019 May 12 See all posts Fast Fourier Transforms Trigger warning: specialized mathematical topicSpecial thanks to Karl Floersch for feedbackOne of the more interesting algorithms in number theory is the Fast Fourier transform (FFT). FFTs are a key building block in many algorithms, including extremely fast multiplication of large numbers, multiplication of polynomials, and extremely fast generation and recovery of erasure codes. Erasure codes in particular are highly versatile; in addition to their basic use cases in fault-tolerant data storage and recovery, erasure codes also have more advanced use cases such as securing data availability in scalable blockchains and STARKs. This article will go into what fast Fourier transforms are, and how some of the simpler algorithms for computing them work.BackgroundThe original Fourier transform is a mathematical operation that is often described as converting data between the "frequency domain" and the "time domain". What this means more precisely is that if you have a piece of data, then running the algorithm would come up with a collection of sine waves with different frequencies and amplitudes that, if you added them together, would approximate the original data. Fourier transforms can be used for such wonderful things as expressing square orbits through epicycles and deriving a set of equations that can draw an elephant: Ok fine, Fourier transforms also have really important applications in signal processing, quantum mechanics, and other areas, and help make significant parts of the global economy happen. But come on, elephants are cooler. Running the Fourier transform algorithm in the "inverse" direction would simply take the sine waves and add them together and compute the resulting values at as many points as you wanted to sample.The kind of Fourier transform we'll be talking about in this post is a similar algorithm, except instead of being a continuous Fourier transform over real or complex numbers, it's a discrete Fourier transform over finite fields (see the "A Modular Math Interlude" section here for a refresher on what finite fields are). Instead of talking about converting between "frequency domain" and "time domain", here we'll talk about two different operations: multi-point polynomial evaluation (evaluating a degree \(< N\) polynomial at \(N\) different points) and its inverse, polynomial interpolation (given the evaluations of a degree \(< N\) polynomial at \(N\) different points, recovering the polynomial). For example, if we are operating in the prime field with modulus 5, then the polynomial \(y = x² + 3\) (for convenience we can write the coefficients in increasing order: \([3,0,1]\)) evaluated at the points \([0,1,2]\) gives the values \([3,4,2]\) (not \([3, 4, 7]\) because we're operating in a finite field where the numbers wrap around at 5), and we can actually take the evaluations \([3,4,2]\) and the coordinates they were evaluated at (\([0,1,2]\)) to recover the original polynomial \([3,0,1]\).There are algorithms for both multi-point evaluation and interpolation that can do either operation in \(O(N^2)\) time. Multi-point evaluation is simple: just separately evaluate the polynomial at each point. Here's python code for doing that:def eval_poly_at(self, poly, x, modulus): y = 0 power_of_x = 1 for coefficient in poly: y += power_of_x * coefficient power_of_x *= x return y % modulusThe algorithm runs a loop going through every coefficient and does one thing for each coefficient, so it runs in \(O(N)\) time. Multi-point evaluation involves doing this evaluation at \(N\) different points, so the total run time is \(O(N^2)\).Lagrange interpolation is more complicated (search for "Lagrange interpolation" here for a more detailed explanation). The key building block of the basic strategy is that for any domain \(D\) and point \(x\), we can construct a polynomial that returns \(1\) for \(x\) and \(0\) for any value in \(D\) other than \(x\). For example, if \(D = [1,2,3,4]\) and \(x = 1\), the polynomial is:\[ y = \frac \]You can mentally plug in \(1\), \(2\), \(3\) and \(4\) to the above expression and verify that it returns \(1\) for \(x= 1\) and \(0\) in the other three cases.We can recover the polynomial that gives any desired set of outputs on the given domain by multiplying and adding these polynomials. If we call the above polynomial \(P_1\), and the equivalent ones for \(x=2\), \(x=3\), \(x=4\), \(P_2\), \(P_3\) and \(P_4\), then the polynomial that returns \([3,1,4,1]\) on the domain \([1,2,3,4]\) is simply \(3 \cdot P_1 + P_2 + 4 \cdot P_3 + P_4\). Computing the \(P_i\) polynomials takes \(O(N^2)\) time (you first construct the polynomial that returns to 0 on the entire domain, which takes \(O(N^2)\) time, then separately divide it by \((x - x_i)\) for each \(x_i\)), and computing the linear combination takes another \(O(N^2)\) time, so it's \(O(N^2)\) runtime total.What Fast Fourier transforms let us do, is make both multi-point evaluation and interpolation much faster.Fast Fourier TransformsThere is a price you have to pay for using this much faster algorithm, which is that you cannot choose any arbitrary field and any arbitrary domain. Whereas with Lagrange interpolation, you could choose whatever x coordinates and y coordinates you wanted, and whatever field you wanted (you could even do it over plain old real numbers), and you could get a polynomial that passes through them., with an FFT, you have to use a finite field, and the domain must be a multiplicative subgroup of the field (that is, a list of powers of some "generator" value). For example, you could use the finite field of integers modulo \(337\), and for the domain use \([1, 85, 148, 111, 336, 252, 189, 226]\) (that's the powers of \(85\) in the field, eg. \(85^3\) % \(337 = 111\); it stops at \(226\) because the next power of \(85\) cycles back to \(1\)). Futhermore, the multiplicative subgroup must have size \(2^n\) (there's ways to make it work for numbers of the form \(2^ \cdot 3^n\) and possibly slightly higher prime powers but then it gets much more complicated and inefficient). The finite field of intergers modulo \(59\), for example, would not work, because there are only multiplicative subgroups of order \(2\), \(29\) and \(58\); \(2\) is too small to be interesting, and the factor \(29\) is far too large to be FFT-friendly. The symmetry that comes from multiplicative groups of size \(2^n\) lets us create a recursive algorithm that quite cleverly calculate the results we need from a much smaller amount of work.To understand the algorithm and why it has a low runtime, it's important to understand the general concept of recursion. A recursive algorithm is an algorithm that has two cases: a "base case" where the input to the algorithm is small enough that you can give the output directly, and the "recursive case" where the required computation consists of some "glue computation" plus one or more uses of the same algorithm to smaller inputs. For example, you might have seen recursive algorithms being used for sorting lists. If you have a list (eg. \([1,8,7,4,5,6,3,2,9]\)), then you can sort it using the following procedure:If the input has one element, then it's already "sorted", so you can just return the input. If the input has more than one element, then separately sort the first half of the list and the second half of the list, and then merge the two sorted sub-lists (call them \(A\) and \(B\)) as follows. Maintain two counters, \(apos\) and \(bpos\), both starting at zero, and maintain an output list, which starts empty. Until either \(apos\) or \(bpos\) is at the end of the corresponding list, check if \(A[apos]\) or \(B[bpos]\) is smaller. Whichever is smaller, add that value to the end of the output list, and increase that counter by \(1\). Once this is done, add the rest of whatever list has not been fully processed to the end of the output list, and return the output list. Note that the "glue" in the second procedure has runtime \(O(N)\): if each of the two sub-lists has \(N\) elements, then you need to run through every item in each list once, so it's \(O(N)\) computation total. So the algorithm as a whole works by taking a problem of size \(N\), and breaking it up into two problems of size \(\frac\), plus \(O(N)\) of "glue" execution. There is a theorem called the Master Theorem that lets us compute the total runtime of algorithms like this. It has many sub-cases, but in the case where you break up an execution of size \(N\) into \(k\) sub-cases of size \(\frac\) with \(O(N)\) glue (as is the case here), the result is that the execution takes time \(O(N \cdot log(N))\). An FFT works in the same way. We take a problem of size \(N\), break it up into two problems of size \(\frac\), and do \(O(N)\) glue work to combine the smaller solutions into a bigger solution, so we get \(O(N \cdot log(N))\) runtime total - much faster than \(O(N^2)\). Here is how we do it. I'll describe first how to use an FFT for multi-point evaluation (ie. for some domain \(D\) and polynomial \(P\), calculate \(P(x)\) for every \(x\) in \(D\)), and it turns out that you can use the same algorithm for interpolation with a minor tweak.Suppose that we have an FFT where the given domain is the powers of \(x\) in some field, where \(x^} = 1\) (eg. in the case we introduced above, the domain is the powers of \(85\) modulo \(337\), and \(85^} = 1\)). We have some polynomial, eg. \(y = 6x^7 + 2x^6 + 9x^5 + 5x^4 + x^3 + 4x^2 + x + 3\) (we'll write it as \(p = [3, 1, 4, 1, 5, 9, 2, 6]\)). We want to evaluate this polynomial at each point in the domain, ie. at each of the eight powers of \(85\). Here is what we do. First, we break up the polynomial into two parts, which we'll call \(evens\) and \(odds\): \(evens = [3, 4, 5, 2]\) and \(odds = [1, 1, 9, 6]\) (or \(evens = 2x^3 + 5x^2 + 4x + 3\) and \(odds = 6x^3 + 9x^2 + x + 1\); yes, this is just taking the even-degree coefficients and the odd-degree coefficients). Now, we note a mathematical observation: \(p(x) = evens(x^2) + x \cdot odds(x^2)\) and \(p(-x) = evens(x^2) - x \cdot odds(x^2)\) (think about this for yourself and make sure you understand it before going further).Here, we have a nice property: \(evens\) and \(odds\) are both polynomials half the size of \(p\), and furthermore, the set of possible values of \(x^2\) is only half the size of the original domain, because there is a two-to-one correspondence: \(x\) and \(-x\) are both part of \(D\) (eg. in our current domain \([1, 85, 148, 111, 336, 252, 189, 226]\), 1 and 336 are negatives of each other, as \(336 = -1\) % \(337\), as are \((85, 252)\), \((148, 189)\) and \((111, 226)\). And \(x\) and \(-x\) always both have the same square. Hence, we can use an FFT to compute the result of \(evens(x)\) for every \(x\) in the smaller domain consisting of squares of numbers in the original domain (\([1, 148, 336, 189]\)), and we can do the same for odds. And voila, we've reduced a size-\(N\) problem into half-size problems.The "glue" is relatively easy (and \(O(N)\) in runtime): we receive the evaluations of \(evens\) and \(odds\) as size-\(\frac\) lists, so we simply do \(p[i] = evens\_result[i] + domain[i]\cdot odds\_result[i]\) and \(p[\frac + i] = evens\_result[i] - domain[i]\cdot odds\_result[i]\) for each index \(i\).Here's the full code:def fft(vals, modulus, domain): if len(vals) == 1: return vals L = fft(vals[::2], modulus, domain[::2]) R = fft(vals[1::2], modulus, domain[::2]) o = [0 for i in vals] for i, (x, y) in enumerate(zip(L, R)): y_times_root = y*domain[i] o[i] = (x+y_times_root) % modulus o[i+len(L)] = (x-y_times_root) % modulus return oWe can try running it:>>> fft([3,1,4,1,5,9,2,6], 337, [1, 85, 148, 111, 336, 252, 189, 226]) [31, 70, 109, 74, 334, 181, 232, 4]And we can check the result; evaluating the polynomial at the position \(85\), for example, actually does give the result \(70\). Note that this only works if the domain is "correct"; it needs to be of the form \([x^i\) % \(modulus\) for \(i\) in \(range(n)]\) where \(x^n = 1\).An inverse FFT is surprisingly simple:def inverse_fft(vals, modulus, domain): vals = fft(vals, modulus, domain) return [x * modular_inverse(len(vals), modulus) % modulus for x in [vals[0]] + vals[1:][::-1]]Basically, run the FFT again, but reverse the result (except the first item stays in place) and divide every value by the length of the list.>>> domain = [1, 85, 148, 111, 336, 252, 189, 226] >>> def modular_inverse(x, n): return pow(x, n - 2, n) >>> values = fft([3,1,4,1,5,9,2,6], 337, domain) >>> values [31, 70, 109, 74, 334, 181, 232, 4] >>> inverse_fft(values, 337, domain) [3, 1, 4, 1, 5, 9, 2, 6]Now, what can we use this for? Here's one fun use case: we can use FFTs to multiply numbers very quickly. Suppose we wanted to multiply \(1253\) by \(1895\). Here is what we would do. First, we would convert the problem into one that turns out to be slightly easier: multiply the polynomials \([3, 5, 2, 1]\) by \([5, 9, 8, 1]\) (that's just the digits of the two numbers in increasing order), and then convert the answer back into a number by doing a single pass to carry over tens digits. We can multiply polynomials with FFTs quickly, because it turns out that if you convert a polynomial into evaluation form (ie. \(f(x)\) for every \(x\) in some domain \(D\)), then you can multiply two polynomials simply by multiplying their evaluations. So what we'll do is take the polynomials representing our two numbers in coefficient form, use FFTs to convert them to evaluation form, multiply them pointwise, and convert back:>>> p1 = [3,5,2,1,0,0,0,0] >>> p2 = [5,9,8,1,0,0,0,0] >>> x1 = fft(p1, 337, domain) >>> x1 [11, 161, 256, 10, 336, 100, 83, 78] >>> x2 = fft(p2, 337, domain) >>> x2 [23, 43, 170, 242, 3, 313, 161, 96] >>> x3 = [(v1 * v2) % 337 for v1, v2 in zip(x1, x2)] >>> x3 [253, 183, 47, 61, 334, 296, 220, 74] >>> inverse_fft(x3, 337, domain) [15, 52, 79, 66, 30, 10, 1, 0]This requires three FFTs (each \(O(N \cdot log(N))\) time) and one pointwise multiplication (\(O(N)\) time), so it takes \(O(N \cdot log(N))\) time altogether (technically a little bit more than \(O(N \cdot log(N))\), because for very big numbers you would need replace \(337\) with a bigger modulus and that would make multiplication harder, but close enough). This is much faster than schoolbook multiplication, which takes \(O(N^2)\) time: 3 5 2 1 ------------ 5 | 15 25 10 5 9 | 27 45 18 9 8 | 24 40 16 8 1 | 3 5 2 1 --------------------- 15 52 79 66 30 10 1 So now we just take the result, and carry the tens digits over (this is a "walk through the list once and do one thing at each point" algorithm so it takes \(O(N)\) time): [15, 52, 79, 66, 30, 10, 1, 0] [ 5, 53, 79, 66, 30, 10, 1, 0] [ 5, 3, 84, 66, 30, 10, 1, 0] [ 5, 3, 4, 74, 30, 10, 1, 0] [ 5, 3, 4, 4, 37, 10, 1, 0] [ 5, 3, 4, 4, 7, 13, 1, 0] [ 5, 3, 4, 4, 7, 3, 2, 0] And if we read the digits from top to bottom, we get \(2374435\). Let's check the answer....>>> 1253 * 1895 2374435Yay! It worked. In practice, on such small inputs, the difference between \(O(N \cdot log(N))\) and \(O(N^2)\) isn't that large, so schoolbook multiplication is faster than this FFT-based multiplication process just because the algorithm is simpler, but on large inputs it makes a really big difference.But FFTs are useful not just for multiplying numbers; as mentioned above, polynomial multiplication and multi-point evaluation are crucially important operations in implementing erasure coding, which is a very important technique for building many kinds of redundant fault-tolerant systems. If you like fault tolerance and you like efficiency, FFTs are your friend.FFTs and binary fieldsPrime fields are not the only kind of finite field out there. Another kind of finite field (really a special case of the more general concept of an extension field, which are kind of like the finite-field equivalent of complex numbers) are binary fields. In an binary field, each element is expressed as a polynomial where all of the entries are \(0\) or \(1\), eg. \(x^3 + x + 1\). Adding polynomials is done modulo \(2\), and subtraction is the same as addition (as \(-1 = 1 \bmod 2\)). We select some irreducible polynomial as a modulus (eg. \(x^4 + x + 1\); \(x^4 + 1\) would not work because \(x^4 + 1\) can be factored into \((x^2 + 1)\cdot(x^2 + 1)\) so it's not "irreducible"); multiplication is done modulo that modulus. For example, in the binary field mod \(x^4 + x + 1\), multiplying \(x^2 + 1\) by \(x^3 + 1\) would give \(x^5 + x^3 + x^2 + 1\) if you just do the multiplication, but \(x^5 + x^3 + x^2 + 1 = (x^4 + x + 1)\cdot x + (x^3 + x + 1)\), so the result is the remainder \(x^3 + x + 1\).We can express this example as a multiplication table. First multiply \([1, 0, 0, 1]\) (ie. \(x^3 + 1\)) by \([1, 0, 1]\) (ie. \(x^2 + 1\)): 1 0 0 1 -------- 1 | 1 0 0 1 0 | 0 0 0 0 1 | 1 0 0 1 ------------ 1 0 1 1 0 1 The multiplication result contains an \(x^5\) term so we can subtract \((x^4 + x + 1)\cdot x\): 1 0 1 1 0 1 - 1 1 0 0 1 [(x⁴ + x + 1) shifted right by one to reflect being multipled by x] ------------ 1 1 0 1 0 0 And we get the result, \([1, 1, 0, 1]\) (or \(x^3 + x + 1\)). Addition and multiplication tables for the binary field mod \(x^4 + x + 1\). Field elements are expressed as integers converted from binary (eg. \(x^3 + x^2 \rightarrow 1100 \rightarrow 12\))Binary fields are interesting for two reasons. First of all, if you want to erasure-code binary data, then binary fields are really convenient because \(N\) bytes of data can be directly encoded as a binary field element, and any binary field elements that you generate by performing computations on it will also be \(N\) bytes long. You cannot do this with prime fields because prime fields' size is not exactly a power of two; for example, you could encode every \(2\) bytes as a number from \(0...65536\) in the prime field modulo \(65537\) (which is prime), but if you do an FFT on these values, then the output could contain \(65536\), which cannot be expressed in two bytes. Second, the fact that addition and subtraction become the same operation, and \(1 + 1 = 0\), create some "structure" which leads to some very interesting consequences. One particularly interesting, and useful, oddity of binary fields is the "freshman's dream" theorem: \((x+y)^2 = x^2 + y^2\) (and the same for exponents \(4, 8, 16...\) basically any power of two).But if you want to use binary fields for erasure coding, and do so efficiently, then you need to be able to do Fast Fourier transforms over binary fields. But then there is a problem: in a binary field, there are no (nontrivial) multiplicative groups of order \(2^n\). This is because the multiplicative groups are all order \(2^n\)-1. For example, in the binary field with modulus \(x^4 + x + 1\), if you start calculating successive powers of \(x+1\), you cycle back to \(1\) after \(\it 15\) steps - not \(16\). The reason is that the total number of elements in the field is \(16\), but one of them is zero, and you're never going to reach zero by multiplying any nonzero value by itself in a field, so the powers of \(x+1\) cycle through every element but zero, so the cycle length is \(15\), not \(16\). So what do we do?The reason we needed the domain to have the "structure" of a multiplicative group with \(2^n\) elements before is that we needed to reduce the size of the domain by a factor of two by squaring each number in it: the domain \([1, 85, 148, 111, 336, 252, 189, 226]\) gets reduced to \([1, 148, 336, 189]\) because \(1\) is the square of both \(1\) and \(336\), \(148\) is the square of both \(85\) and \(252\), and so forth. But what if in a binary field there's a different way to halve the size of a domain? It turns out that there is: given a domain containing \(2^k\) values, including zero (technically the domain must be a subspace), we can construct a half-sized new domain \(D'\) by taking \(x \cdot (x+k)\) for \(x\) in \(D\) using some specific \(k\) in \(D\). Because the original domain is a subspace, since \(k\) is in the domain, any \(x\) in the domain has a corresponding \(x+k\) also in the domain, and the function \(f(x) = x \cdot (x+k)\) returns the same value for \(x\) and \(x+k\) so we get the same kind of two-to-one correspondence that squaring gives us. \(x\) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 \(x \cdot (x+1)\) 0 0 6 6 7 7 1 1 4 4 2 2 3 3 5 5 So now, how do we do an FFT on top of this? We'll use the same trick, converting a problem with an \(N\)-sized polynomial and \(N\)-sized domain into two problems each with an \(\frac\)-sized polynomial and \(\frac\)-sized domain, but this time using different equations. We'll convert a polynomial \(p\) into two polynomials \(evens\) and \(odds\) such that \(p(x) = evens(x \cdot (k-x)) + x \cdot odds(x \cdot (k-x))\). Note that for the \(evens\) and \(odds\) that we find, it will also be true that \(p(x+k) = evens(x \cdot (k-x)) + (x+k) \cdot odds(x \cdot (k-x))\). So we can then recursively do an FFT to \(evens\) and \(odds\) on the reduced domain \([x \cdot (k-x)\) for \(x\) in \(D]\), and then we use these two formulas to get the answers for two "halves" of the domain, one offset by \(k\) from the other.Converting \(p\) into \(evens\) and \(odds\) as described above turns out to itself be nontrivial. The "naive" algorithm for doing this is itself \(O(N^2)\), but it turns out that in a binary field, we can use the fact that \((x^2-kx)^2 = x^4 - k^2 \cdot x^2\), and more generally \((x^2-kx)^} = x^} - k^} \cdot x^}\) , to create yet another recursive algorithm to do this in \(O(N \cdot log(N))\) time.And if you want to do an inverse FFT, to do interpolation, then you need to run the steps in the algorithm in reverse order. You can find the complete code for doing this here: https://github.com/ethereum/research/tree/master/binary_fft, and a paper with details on more optimal algorithms here: http://www.math.clemson.edu/~sgao/papers/GM10.pdfSo what do we get from all of this complexity? Well, we can try running the implementation, which features both a "naive" \(O(N^2)\) multi-point evaluation and the optimized FFT-based one, and time both. Here are my results:>>> import binary_fft as b >>> import time, random >>> f = b.BinaryField(1033) >>> poly = [random.randrange(1024) for i in range(1024)] >>> a = time.time(); x1 = b._simple_ft(f, poly); time.time() - a 0.5752472877502441 >>> a = time.time(); x2 = b.fft(f, poly, list(range(1024))); time.time() - a 0.03820443153381348And as the size of the polynomial gets larger, the naive implementation (_simple_ft) gets slower much more quickly than the FFT:>>> f = b.BinaryField(2053) >>> poly = [random.randrange(2048) for i in range(2048)] >>> a = time.time(); x1 = b._simple_ft(f, poly); time.time() - a 2.2243144512176514 >>> a = time.time(); x2 = b.fft(f, poly, list(range(2048))); time.time() - a 0.07896280288696289And voila, we have an efficient, scalable way to multi-point evaluate and interpolate polynomials. If we want to use FFTs to recover erasure-coded data where we are missing some pieces, then algorithms for this also exist, though they are somewhat less efficient than just doing a single FFT. Enjoy!
Fast Fourier Transforms Fast Fourier Transforms2019 May 12 See all posts Fast Fourier Transforms Trigger warning: specialized mathematical topicSpecial thanks to Karl Floersch for feedbackOne of the more interesting algorithms in number theory is the Fast Fourier transform (FFT). FFTs are a key building block in many algorithms, including extremely fast multiplication of large numbers, multiplication of polynomials, and extremely fast generation and recovery of erasure codes. Erasure codes in particular are highly versatile; in addition to their basic use cases in fault-tolerant data storage and recovery, erasure codes also have more advanced use cases such as securing data availability in scalable blockchains and STARKs. This article will go into what fast Fourier transforms are, and how some of the simpler algorithms for computing them work.BackgroundThe original Fourier transform is a mathematical operation that is often described as converting data between the "frequency domain" and the "time domain". What this means more precisely is that if you have a piece of data, then running the algorithm would come up with a collection of sine waves with different frequencies and amplitudes that, if you added them together, would approximate the original data. Fourier transforms can be used for such wonderful things as expressing square orbits through epicycles and deriving a set of equations that can draw an elephant: Ok fine, Fourier transforms also have really important applications in signal processing, quantum mechanics, and other areas, and help make significant parts of the global economy happen. But come on, elephants are cooler. Running the Fourier transform algorithm in the "inverse" direction would simply take the sine waves and add them together and compute the resulting values at as many points as you wanted to sample.The kind of Fourier transform we'll be talking about in this post is a similar algorithm, except instead of being a continuous Fourier transform over real or complex numbers, it's a discrete Fourier transform over finite fields (see the "A Modular Math Interlude" section here for a refresher on what finite fields are). Instead of talking about converting between "frequency domain" and "time domain", here we'll talk about two different operations: multi-point polynomial evaluation (evaluating a degree \(< N\) polynomial at \(N\) different points) and its inverse, polynomial interpolation (given the evaluations of a degree \(< N\) polynomial at \(N\) different points, recovering the polynomial). For example, if we are operating in the prime field with modulus 5, then the polynomial \(y = x² + 3\) (for convenience we can write the coefficients in increasing order: \([3,0,1]\)) evaluated at the points \([0,1,2]\) gives the values \([3,4,2]\) (not \([3, 4, 7]\) because we're operating in a finite field where the numbers wrap around at 5), and we can actually take the evaluations \([3,4,2]\) and the coordinates they were evaluated at (\([0,1,2]\)) to recover the original polynomial \([3,0,1]\).There are algorithms for both multi-point evaluation and interpolation that can do either operation in \(O(N^2)\) time. Multi-point evaluation is simple: just separately evaluate the polynomial at each point. Here's python code for doing that:def eval_poly_at(self, poly, x, modulus): y = 0 power_of_x = 1 for coefficient in poly: y += power_of_x * coefficient power_of_x *= x return y % modulusThe algorithm runs a loop going through every coefficient and does one thing for each coefficient, so it runs in \(O(N)\) time. Multi-point evaluation involves doing this evaluation at \(N\) different points, so the total run time is \(O(N^2)\).Lagrange interpolation is more complicated (search for "Lagrange interpolation" here for a more detailed explanation). The key building block of the basic strategy is that for any domain \(D\) and point \(x\), we can construct a polynomial that returns \(1\) for \(x\) and \(0\) for any value in \(D\) other than \(x\). For example, if \(D = [1,2,3,4]\) and \(x = 1\), the polynomial is:\[ y = \frac \]You can mentally plug in \(1\), \(2\), \(3\) and \(4\) to the above expression and verify that it returns \(1\) for \(x= 1\) and \(0\) in the other three cases.We can recover the polynomial that gives any desired set of outputs on the given domain by multiplying and adding these polynomials. If we call the above polynomial \(P_1\), and the equivalent ones for \(x=2\), \(x=3\), \(x=4\), \(P_2\), \(P_3\) and \(P_4\), then the polynomial that returns \([3,1,4,1]\) on the domain \([1,2,3,4]\) is simply \(3 \cdot P_1 + P_2 + 4 \cdot P_3 + P_4\). Computing the \(P_i\) polynomials takes \(O(N^2)\) time (you first construct the polynomial that returns to 0 on the entire domain, which takes \(O(N^2)\) time, then separately divide it by \((x - x_i)\) for each \(x_i\)), and computing the linear combination takes another \(O(N^2)\) time, so it's \(O(N^2)\) runtime total.What Fast Fourier transforms let us do, is make both multi-point evaluation and interpolation much faster.Fast Fourier TransformsThere is a price you have to pay for using this much faster algorithm, which is that you cannot choose any arbitrary field and any arbitrary domain. Whereas with Lagrange interpolation, you could choose whatever x coordinates and y coordinates you wanted, and whatever field you wanted (you could even do it over plain old real numbers), and you could get a polynomial that passes through them., with an FFT, you have to use a finite field, and the domain must be a multiplicative subgroup of the field (that is, a list of powers of some "generator" value). For example, you could use the finite field of integers modulo \(337\), and for the domain use \([1, 85, 148, 111, 336, 252, 189, 226]\) (that's the powers of \(85\) in the field, eg. \(85^3\) % \(337 = 111\); it stops at \(226\) because the next power of \(85\) cycles back to \(1\)). Futhermore, the multiplicative subgroup must have size \(2^n\) (there's ways to make it work for numbers of the form \(2^ \cdot 3^n\) and possibly slightly higher prime powers but then it gets much more complicated and inefficient). The finite field of intergers modulo \(59\), for example, would not work, because there are only multiplicative subgroups of order \(2\), \(29\) and \(58\); \(2\) is too small to be interesting, and the factor \(29\) is far too large to be FFT-friendly. The symmetry that comes from multiplicative groups of size \(2^n\) lets us create a recursive algorithm that quite cleverly calculate the results we need from a much smaller amount of work.To understand the algorithm and why it has a low runtime, it's important to understand the general concept of recursion. A recursive algorithm is an algorithm that has two cases: a "base case" where the input to the algorithm is small enough that you can give the output directly, and the "recursive case" where the required computation consists of some "glue computation" plus one or more uses of the same algorithm to smaller inputs. For example, you might have seen recursive algorithms being used for sorting lists. If you have a list (eg. \([1,8,7,4,5,6,3,2,9]\)), then you can sort it using the following procedure:If the input has one element, then it's already "sorted", so you can just return the input. If the input has more than one element, then separately sort the first half of the list and the second half of the list, and then merge the two sorted sub-lists (call them \(A\) and \(B\)) as follows. Maintain two counters, \(apos\) and \(bpos\), both starting at zero, and maintain an output list, which starts empty. Until either \(apos\) or \(bpos\) is at the end of the corresponding list, check if \(A[apos]\) or \(B[bpos]\) is smaller. Whichever is smaller, add that value to the end of the output list, and increase that counter by \(1\). Once this is done, add the rest of whatever list has not been fully processed to the end of the output list, and return the output list. Note that the "glue" in the second procedure has runtime \(O(N)\): if each of the two sub-lists has \(N\) elements, then you need to run through every item in each list once, so it's \(O(N)\) computation total. So the algorithm as a whole works by taking a problem of size \(N\), and breaking it up into two problems of size \(\frac\), plus \(O(N)\) of "glue" execution. There is a theorem called the Master Theorem that lets us compute the total runtime of algorithms like this. It has many sub-cases, but in the case where you break up an execution of size \(N\) into \(k\) sub-cases of size \(\frac\) with \(O(N)\) glue (as is the case here), the result is that the execution takes time \(O(N \cdot log(N))\). An FFT works in the same way. We take a problem of size \(N\), break it up into two problems of size \(\frac\), and do \(O(N)\) glue work to combine the smaller solutions into a bigger solution, so we get \(O(N \cdot log(N))\) runtime total - much faster than \(O(N^2)\). Here is how we do it. I'll describe first how to use an FFT for multi-point evaluation (ie. for some domain \(D\) and polynomial \(P\), calculate \(P(x)\) for every \(x\) in \(D\)), and it turns out that you can use the same algorithm for interpolation with a minor tweak.Suppose that we have an FFT where the given domain is the powers of \(x\) in some field, where \(x^} = 1\) (eg. in the case we introduced above, the domain is the powers of \(85\) modulo \(337\), and \(85^} = 1\)). We have some polynomial, eg. \(y = 6x^7 + 2x^6 + 9x^5 + 5x^4 + x^3 + 4x^2 + x + 3\) (we'll write it as \(p = [3, 1, 4, 1, 5, 9, 2, 6]\)). We want to evaluate this polynomial at each point in the domain, ie. at each of the eight powers of \(85\). Here is what we do. First, we break up the polynomial into two parts, which we'll call \(evens\) and \(odds\): \(evens = [3, 4, 5, 2]\) and \(odds = [1, 1, 9, 6]\) (or \(evens = 2x^3 + 5x^2 + 4x + 3\) and \(odds = 6x^3 + 9x^2 + x + 1\); yes, this is just taking the even-degree coefficients and the odd-degree coefficients). Now, we note a mathematical observation: \(p(x) = evens(x^2) + x \cdot odds(x^2)\) and \(p(-x) = evens(x^2) - x \cdot odds(x^2)\) (think about this for yourself and make sure you understand it before going further).Here, we have a nice property: \(evens\) and \(odds\) are both polynomials half the size of \(p\), and furthermore, the set of possible values of \(x^2\) is only half the size of the original domain, because there is a two-to-one correspondence: \(x\) and \(-x\) are both part of \(D\) (eg. in our current domain \([1, 85, 148, 111, 336, 252, 189, 226]\), 1 and 336 are negatives of each other, as \(336 = -1\) % \(337\), as are \((85, 252)\), \((148, 189)\) and \((111, 226)\). And \(x\) and \(-x\) always both have the same square. Hence, we can use an FFT to compute the result of \(evens(x)\) for every \(x\) in the smaller domain consisting of squares of numbers in the original domain (\([1, 148, 336, 189]\)), and we can do the same for odds. And voila, we've reduced a size-\(N\) problem into half-size problems.The "glue" is relatively easy (and \(O(N)\) in runtime): we receive the evaluations of \(evens\) and \(odds\) as size-\(\frac\) lists, so we simply do \(p[i] = evens\_result[i] + domain[i]\cdot odds\_result[i]\) and \(p[\frac + i] = evens\_result[i] - domain[i]\cdot odds\_result[i]\) for each index \(i\).Here's the full code:def fft(vals, modulus, domain): if len(vals) == 1: return vals L = fft(vals[::2], modulus, domain[::2]) R = fft(vals[1::2], modulus, domain[::2]) o = [0 for i in vals] for i, (x, y) in enumerate(zip(L, R)): y_times_root = y*domain[i] o[i] = (x+y_times_root) % modulus o[i+len(L)] = (x-y_times_root) % modulus return oWe can try running it:>>> fft([3,1,4,1,5,9,2,6], 337, [1, 85, 148, 111, 336, 252, 189, 226]) [31, 70, 109, 74, 334, 181, 232, 4]And we can check the result; evaluating the polynomial at the position \(85\), for example, actually does give the result \(70\). Note that this only works if the domain is "correct"; it needs to be of the form \([x^i\) % \(modulus\) for \(i\) in \(range(n)]\) where \(x^n = 1\).An inverse FFT is surprisingly simple:def inverse_fft(vals, modulus, domain): vals = fft(vals, modulus, domain) return [x * modular_inverse(len(vals), modulus) % modulus for x in [vals[0]] + vals[1:][::-1]]Basically, run the FFT again, but reverse the result (except the first item stays in place) and divide every value by the length of the list.>>> domain = [1, 85, 148, 111, 336, 252, 189, 226] >>> def modular_inverse(x, n): return pow(x, n - 2, n) >>> values = fft([3,1,4,1,5,9,2,6], 337, domain) >>> values [31, 70, 109, 74, 334, 181, 232, 4] >>> inverse_fft(values, 337, domain) [3, 1, 4, 1, 5, 9, 2, 6]Now, what can we use this for? Here's one fun use case: we can use FFTs to multiply numbers very quickly. Suppose we wanted to multiply \(1253\) by \(1895\). Here is what we would do. First, we would convert the problem into one that turns out to be slightly easier: multiply the polynomials \([3, 5, 2, 1]\) by \([5, 9, 8, 1]\) (that's just the digits of the two numbers in increasing order), and then convert the answer back into a number by doing a single pass to carry over tens digits. We can multiply polynomials with FFTs quickly, because it turns out that if you convert a polynomial into evaluation form (ie. \(f(x)\) for every \(x\) in some domain \(D\)), then you can multiply two polynomials simply by multiplying their evaluations. So what we'll do is take the polynomials representing our two numbers in coefficient form, use FFTs to convert them to evaluation form, multiply them pointwise, and convert back:>>> p1 = [3,5,2,1,0,0,0,0] >>> p2 = [5,9,8,1,0,0,0,0] >>> x1 = fft(p1, 337, domain) >>> x1 [11, 161, 256, 10, 336, 100, 83, 78] >>> x2 = fft(p2, 337, domain) >>> x2 [23, 43, 170, 242, 3, 313, 161, 96] >>> x3 = [(v1 * v2) % 337 for v1, v2 in zip(x1, x2)] >>> x3 [253, 183, 47, 61, 334, 296, 220, 74] >>> inverse_fft(x3, 337, domain) [15, 52, 79, 66, 30, 10, 1, 0]This requires three FFTs (each \(O(N \cdot log(N))\) time) and one pointwise multiplication (\(O(N)\) time), so it takes \(O(N \cdot log(N))\) time altogether (technically a little bit more than \(O(N \cdot log(N))\), because for very big numbers you would need replace \(337\) with a bigger modulus and that would make multiplication harder, but close enough). This is much faster than schoolbook multiplication, which takes \(O(N^2)\) time: 3 5 2 1 ------------ 5 | 15 25 10 5 9 | 27 45 18 9 8 | 24 40 16 8 1 | 3 5 2 1 --------------------- 15 52 79 66 30 10 1 So now we just take the result, and carry the tens digits over (this is a "walk through the list once and do one thing at each point" algorithm so it takes \(O(N)\) time): [15, 52, 79, 66, 30, 10, 1, 0] [ 5, 53, 79, 66, 30, 10, 1, 0] [ 5, 3, 84, 66, 30, 10, 1, 0] [ 5, 3, 4, 74, 30, 10, 1, 0] [ 5, 3, 4, 4, 37, 10, 1, 0] [ 5, 3, 4, 4, 7, 13, 1, 0] [ 5, 3, 4, 4, 7, 3, 2, 0] And if we read the digits from top to bottom, we get \(2374435\). Let's check the answer....>>> 1253 * 1895 2374435Yay! It worked. In practice, on such small inputs, the difference between \(O(N \cdot log(N))\) and \(O(N^2)\) isn't that large, so schoolbook multiplication is faster than this FFT-based multiplication process just because the algorithm is simpler, but on large inputs it makes a really big difference.But FFTs are useful not just for multiplying numbers; as mentioned above, polynomial multiplication and multi-point evaluation are crucially important operations in implementing erasure coding, which is a very important technique for building many kinds of redundant fault-tolerant systems. If you like fault tolerance and you like efficiency, FFTs are your friend.FFTs and binary fieldsPrime fields are not the only kind of finite field out there. Another kind of finite field (really a special case of the more general concept of an extension field, which are kind of like the finite-field equivalent of complex numbers) are binary fields. In an binary field, each element is expressed as a polynomial where all of the entries are \(0\) or \(1\), eg. \(x^3 + x + 1\). Adding polynomials is done modulo \(2\), and subtraction is the same as addition (as \(-1 = 1 \bmod 2\)). We select some irreducible polynomial as a modulus (eg. \(x^4 + x + 1\); \(x^4 + 1\) would not work because \(x^4 + 1\) can be factored into \((x^2 + 1)\cdot(x^2 + 1)\) so it's not "irreducible"); multiplication is done modulo that modulus. For example, in the binary field mod \(x^4 + x + 1\), multiplying \(x^2 + 1\) by \(x^3 + 1\) would give \(x^5 + x^3 + x^2 + 1\) if you just do the multiplication, but \(x^5 + x^3 + x^2 + 1 = (x^4 + x + 1)\cdot x + (x^3 + x + 1)\), so the result is the remainder \(x^3 + x + 1\).We can express this example as a multiplication table. First multiply \([1, 0, 0, 1]\) (ie. \(x^3 + 1\)) by \([1, 0, 1]\) (ie. \(x^2 + 1\)): 1 0 0 1 -------- 1 | 1 0 0 1 0 | 0 0 0 0 1 | 1 0 0 1 ------------ 1 0 1 1 0 1 The multiplication result contains an \(x^5\) term so we can subtract \((x^4 + x + 1)\cdot x\): 1 0 1 1 0 1 - 1 1 0 0 1 [(x⁴ + x + 1) shifted right by one to reflect being multipled by x] ------------ 1 1 0 1 0 0 And we get the result, \([1, 1, 0, 1]\) (or \(x^3 + x + 1\)). Addition and multiplication tables for the binary field mod \(x^4 + x + 1\). Field elements are expressed as integers converted from binary (eg. \(x^3 + x^2 \rightarrow 1100 \rightarrow 12\))Binary fields are interesting for two reasons. First of all, if you want to erasure-code binary data, then binary fields are really convenient because \(N\) bytes of data can be directly encoded as a binary field element, and any binary field elements that you generate by performing computations on it will also be \(N\) bytes long. You cannot do this with prime fields because prime fields' size is not exactly a power of two; for example, you could encode every \(2\) bytes as a number from \(0...65536\) in the prime field modulo \(65537\) (which is prime), but if you do an FFT on these values, then the output could contain \(65536\), which cannot be expressed in two bytes. Second, the fact that addition and subtraction become the same operation, and \(1 + 1 = 0\), create some "structure" which leads to some very interesting consequences. One particularly interesting, and useful, oddity of binary fields is the "freshman's dream" theorem: \((x+y)^2 = x^2 + y^2\) (and the same for exponents \(4, 8, 16...\) basically any power of two).But if you want to use binary fields for erasure coding, and do so efficiently, then you need to be able to do Fast Fourier transforms over binary fields. But then there is a problem: in a binary field, there are no (nontrivial) multiplicative groups of order \(2^n\). This is because the multiplicative groups are all order \(2^n\)-1. For example, in the binary field with modulus \(x^4 + x + 1\), if you start calculating successive powers of \(x+1\), you cycle back to \(1\) after \(\it 15\) steps - not \(16\). The reason is that the total number of elements in the field is \(16\), but one of them is zero, and you're never going to reach zero by multiplying any nonzero value by itself in a field, so the powers of \(x+1\) cycle through every element but zero, so the cycle length is \(15\), not \(16\). So what do we do?The reason we needed the domain to have the "structure" of a multiplicative group with \(2^n\) elements before is that we needed to reduce the size of the domain by a factor of two by squaring each number in it: the domain \([1, 85, 148, 111, 336, 252, 189, 226]\) gets reduced to \([1, 148, 336, 189]\) because \(1\) is the square of both \(1\) and \(336\), \(148\) is the square of both \(85\) and \(252\), and so forth. But what if in a binary field there's a different way to halve the size of a domain? It turns out that there is: given a domain containing \(2^k\) values, including zero (technically the domain must be a subspace), we can construct a half-sized new domain \(D'\) by taking \(x \cdot (x+k)\) for \(x\) in \(D\) using some specific \(k\) in \(D\). Because the original domain is a subspace, since \(k\) is in the domain, any \(x\) in the domain has a corresponding \(x+k\) also in the domain, and the function \(f(x) = x \cdot (x+k)\) returns the same value for \(x\) and \(x+k\) so we get the same kind of two-to-one correspondence that squaring gives us. \(x\) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 \(x \cdot (x+1)\) 0 0 6 6 7 7 1 1 4 4 2 2 3 3 5 5 So now, how do we do an FFT on top of this? We'll use the same trick, converting a problem with an \(N\)-sized polynomial and \(N\)-sized domain into two problems each with an \(\frac\)-sized polynomial and \(\frac\)-sized domain, but this time using different equations. We'll convert a polynomial \(p\) into two polynomials \(evens\) and \(odds\) such that \(p(x) = evens(x \cdot (k-x)) + x \cdot odds(x \cdot (k-x))\). Note that for the \(evens\) and \(odds\) that we find, it will also be true that \(p(x+k) = evens(x \cdot (k-x)) + (x+k) \cdot odds(x \cdot (k-x))\). So we can then recursively do an FFT to \(evens\) and \(odds\) on the reduced domain \([x \cdot (k-x)\) for \(x\) in \(D]\), and then we use these two formulas to get the answers for two "halves" of the domain, one offset by \(k\) from the other.Converting \(p\) into \(evens\) and \(odds\) as described above turns out to itself be nontrivial. The "naive" algorithm for doing this is itself \(O(N^2)\), but it turns out that in a binary field, we can use the fact that \((x^2-kx)^2 = x^4 - k^2 \cdot x^2\), and more generally \((x^2-kx)^} = x^} - k^} \cdot x^}\) , to create yet another recursive algorithm to do this in \(O(N \cdot log(N))\) time.And if you want to do an inverse FFT, to do interpolation, then you need to run the steps in the algorithm in reverse order. You can find the complete code for doing this here: https://github.com/ethereum/research/tree/master/binary_fft, and a paper with details on more optimal algorithms here: http://www.math.clemson.edu/~sgao/papers/GM10.pdfSo what do we get from all of this complexity? Well, we can try running the implementation, which features both a "naive" \(O(N^2)\) multi-point evaluation and the optimized FFT-based one, and time both. Here are my results:>>> import binary_fft as b >>> import time, random >>> f = b.BinaryField(1033) >>> poly = [random.randrange(1024) for i in range(1024)] >>> a = time.time(); x1 = b._simple_ft(f, poly); time.time() - a 0.5752472877502441 >>> a = time.time(); x2 = b.fft(f, poly, list(range(1024))); time.time() - a 0.03820443153381348And as the size of the polynomial gets larger, the naive implementation (_simple_ft) gets slower much more quickly than the FFT:>>> f = b.BinaryField(2053) >>> poly = [random.randrange(2048) for i in range(2048)] >>> a = time.time(); x1 = b._simple_ft(f, poly); time.time() - a 2.2243144512176514 >>> a = time.time(); x2 = b.fft(f, poly, list(range(2048))); time.time() - a 0.07896280288696289And voila, we have an efficient, scalable way to multi-point evaluate and interpolate polynomials. If we want to use FFTs to recover erasure-coded data where we are missing some pieces, then algorithms for this also exist, though they are somewhat less efficient than just doing a single FFT. Enjoy! -
 Control as Liability Control as Liability2019 May 09 See all posts Control as Liability The regulatory and legal environment around internet-based services and applications has changed considerably over the last decade. When large-scale social networking platforms first became popular in the 2000s, the general attitude toward mass data collection was essentially "why not?". This was the age of Mark Zuckerberg saying the age of privacy is over and Eric Schmidt arguing, "If you have something that you don't want anyone to know, maybe you shouldn't be doing it in the first place." And it made personal sense for them to argue this: every bit of data you can get about others was a potential machine learning advantage for you, every single restriction a weakness, and if something happened to that data, the costs were relatively minor. Ten years later, things are very different.It is especially worth zooming in on a few particular trends.Privacy. Over the last ten years, a number of privacy laws have been passed, most aggressively in Europe but also elsewhere, but the most recent is the GDPR. The GDPR has many parts, but among the most prominent are: (i) requirements for explicit consent, (ii) requirement to have a legal basis to process data, (iii) users' right to download all their data, (iv) users' right to require you to delete all their data. Other jurisdictions are exploring similar rules. Data localization rules. India, Russia and many other jurisdictions increasingly have or are exploring rules that require data on users within the country to be stored inside the country. And even when explicit laws do not exist, there's a growing shift toward concern (eg. 1 2) around data being moved to countries that are perceived to not sufficiently protect it. Sharing economy regulation. Sharing economy companies such as Uber are having a hard time arguing to courts that, given the extent to which their applications control and direct drivers' activity, they should not be legally classified as employers. Cryptocurrency regulation. A recent FINCEN guidance attempts to clarify what categories of cryptocurrency-related activity are and are not subject to regulatory licensing requirements in the United States. Running a hosted wallet? Regulated. Running a wallet where the user controls their funds? Not regulated. Running an anonymizing mixing service? If you're running it, regulated. If you're just writing code... not regulated. As Emin Gun Sirer points out, the FINCEN cryptocurrency guidance is not at all haphazard; rather, it's trying to separate out categories of applications where the developer is actively controlling funds, from applications where the developer has no control. The guidance carefully separates out how multisignature wallets, where keys are held both by the operator and the user, are sometimes regulated and sometimes not:If the multiple-signature wallet provider restricts its role to creating un-hosted wallets that require adding a second authorization key to the wallet owner's private key in order to validate and complete transactions, the provider is not a money transmitter because it does not accept and transmit value. On the other hand, if ... the value is represented as an entry in the accounts of the provider, the owner does not interact with the payment system directly, or the provider maintains total independent control of the value, the provider will also qualify as a money transmitter.Although these events are taking place across a variety of contexts and industries, I would argue that there is a common trend at play. And the trend is this: control over users' data and digital possessions and activity is rapidly moving from an asset to a liability. Before, every bit of control you have was good: it gives you more flexibility to earn revenue, if not now then in the future. Now, every bit of control you have is a liability: you might be regulated because of it. If you exhibit control over your users' cryptocurrency, you are a money transmitter. If you have "sole discretion over fares, and can charge drivers a cancellation fee if they choose not to take a ride, prohibit drivers from picking up passengers not using the app and suspend or deactivate drivers' accounts", you are an employer. If you control your users' data, you're required to make sure you can argue just cause, have a compliance officer, and give your users access to download or delete the data.If you are an application builder, and you are both lazy and fear legal trouble, there is one easy way to make sure that you violate none of the above new rules: don't build applications that centralize control. If you build a wallet where the user holds their private keys, you really are still "just a software provider". If you build a "decentralized Uber" that really is just a slick UI combining a payment system, a reputation system and a search engine, and don't control the components yourself, you really won't get hit by many of the same legal issues. If you build a website that just... doesn't collect data (Static web pages? But that's impossible!) you don't have to even think about the GDPR.This kind of approach is of course not realistic for everyone. There will continue to be many cases where going without the conveniences of centralized control simply sacrifices too much for both developers and users, and there are also cases where the business model considerations mandate a more centralized approach (eg. it's easier to prevent non-paying users from using software if the software stays on your servers) win out. But we're definitely very far from having explored the full range of possibilities that more decentralized approaches offer.Generally, unintended consequences of laws, discouraging entire categories of activity when one wanted to only surgically forbid a few specific things, are considered to be a bad thing. Here though, I would argue that the forced shift in developers' mindsets, from "I want to control more things just in case" to "I want to control fewer things just in case", also has many positive consequences. Voluntarily giving up control, and voluntarily taking steps to deprive oneself of the ability to do mischief, does not come naturally to many people, and while ideologically-driven decentralization-maximizing projects exist today, it's not at all obvious at first glance that such services will continue to dominate as the industry mainstreams. What this trend in regulation does, however, is that it gives a big nudge in favor of those applications that are willing to take the centralization-minimizing, user-sovereignty-maximizing "can't be evil" route.Hence, even though these regulatory changes are arguably not pro-freedom, at least if one is concerned with the freedom of application developers, and the transformation of the internet into a subject of political focus is bound to have many negative knock-on effects, the particular trend of control becoming a liability is in a strange way even more pro-cypherpunk (even if not intentionally!) than policies of maximizing total freedom for application developers would have been. Though the present-day regulatory landscape is very far from an optimal one from the point of view of almost anyone's preferences, it has unintentionally dealt the movement for minimizing unneeded centralization and maximizing users' control of their own assets, private keys and data a surprisingly strong hand to execute on its vision. And it would be highly beneficial to the movement to take advantage of it.
Control as Liability Control as Liability2019 May 09 See all posts Control as Liability The regulatory and legal environment around internet-based services and applications has changed considerably over the last decade. When large-scale social networking platforms first became popular in the 2000s, the general attitude toward mass data collection was essentially "why not?". This was the age of Mark Zuckerberg saying the age of privacy is over and Eric Schmidt arguing, "If you have something that you don't want anyone to know, maybe you shouldn't be doing it in the first place." And it made personal sense for them to argue this: every bit of data you can get about others was a potential machine learning advantage for you, every single restriction a weakness, and if something happened to that data, the costs were relatively minor. Ten years later, things are very different.It is especially worth zooming in on a few particular trends.Privacy. Over the last ten years, a number of privacy laws have been passed, most aggressively in Europe but also elsewhere, but the most recent is the GDPR. The GDPR has many parts, but among the most prominent are: (i) requirements for explicit consent, (ii) requirement to have a legal basis to process data, (iii) users' right to download all their data, (iv) users' right to require you to delete all their data. Other jurisdictions are exploring similar rules. Data localization rules. India, Russia and many other jurisdictions increasingly have or are exploring rules that require data on users within the country to be stored inside the country. And even when explicit laws do not exist, there's a growing shift toward concern (eg. 1 2) around data being moved to countries that are perceived to not sufficiently protect it. Sharing economy regulation. Sharing economy companies such as Uber are having a hard time arguing to courts that, given the extent to which their applications control and direct drivers' activity, they should not be legally classified as employers. Cryptocurrency regulation. A recent FINCEN guidance attempts to clarify what categories of cryptocurrency-related activity are and are not subject to regulatory licensing requirements in the United States. Running a hosted wallet? Regulated. Running a wallet where the user controls their funds? Not regulated. Running an anonymizing mixing service? If you're running it, regulated. If you're just writing code... not regulated. As Emin Gun Sirer points out, the FINCEN cryptocurrency guidance is not at all haphazard; rather, it's trying to separate out categories of applications where the developer is actively controlling funds, from applications where the developer has no control. The guidance carefully separates out how multisignature wallets, where keys are held both by the operator and the user, are sometimes regulated and sometimes not:If the multiple-signature wallet provider restricts its role to creating un-hosted wallets that require adding a second authorization key to the wallet owner's private key in order to validate and complete transactions, the provider is not a money transmitter because it does not accept and transmit value. On the other hand, if ... the value is represented as an entry in the accounts of the provider, the owner does not interact with the payment system directly, or the provider maintains total independent control of the value, the provider will also qualify as a money transmitter.Although these events are taking place across a variety of contexts and industries, I would argue that there is a common trend at play. And the trend is this: control over users' data and digital possessions and activity is rapidly moving from an asset to a liability. Before, every bit of control you have was good: it gives you more flexibility to earn revenue, if not now then in the future. Now, every bit of control you have is a liability: you might be regulated because of it. If you exhibit control over your users' cryptocurrency, you are a money transmitter. If you have "sole discretion over fares, and can charge drivers a cancellation fee if they choose not to take a ride, prohibit drivers from picking up passengers not using the app and suspend or deactivate drivers' accounts", you are an employer. If you control your users' data, you're required to make sure you can argue just cause, have a compliance officer, and give your users access to download or delete the data.If you are an application builder, and you are both lazy and fear legal trouble, there is one easy way to make sure that you violate none of the above new rules: don't build applications that centralize control. If you build a wallet where the user holds their private keys, you really are still "just a software provider". If you build a "decentralized Uber" that really is just a slick UI combining a payment system, a reputation system and a search engine, and don't control the components yourself, you really won't get hit by many of the same legal issues. If you build a website that just... doesn't collect data (Static web pages? But that's impossible!) you don't have to even think about the GDPR.This kind of approach is of course not realistic for everyone. There will continue to be many cases where going without the conveniences of centralized control simply sacrifices too much for both developers and users, and there are also cases where the business model considerations mandate a more centralized approach (eg. it's easier to prevent non-paying users from using software if the software stays on your servers) win out. But we're definitely very far from having explored the full range of possibilities that more decentralized approaches offer.Generally, unintended consequences of laws, discouraging entire categories of activity when one wanted to only surgically forbid a few specific things, are considered to be a bad thing. Here though, I would argue that the forced shift in developers' mindsets, from "I want to control more things just in case" to "I want to control fewer things just in case", also has many positive consequences. Voluntarily giving up control, and voluntarily taking steps to deprive oneself of the ability to do mischief, does not come naturally to many people, and while ideologically-driven decentralization-maximizing projects exist today, it's not at all obvious at first glance that such services will continue to dominate as the industry mainstreams. What this trend in regulation does, however, is that it gives a big nudge in favor of those applications that are willing to take the centralization-minimizing, user-sovereignty-maximizing "can't be evil" route.Hence, even though these regulatory changes are arguably not pro-freedom, at least if one is concerned with the freedom of application developers, and the transformation of the internet into a subject of political focus is bound to have many negative knock-on effects, the particular trend of control becoming a liability is in a strange way even more pro-cypherpunk (even if not intentionally!) than policies of maximizing total freedom for application developers would have been. Though the present-day regulatory landscape is very far from an optimal one from the point of view of almost anyone's preferences, it has unintentionally dealt the movement for minimizing unneeded centralization and maximizing users' control of their own assets, private keys and data a surprisingly strong hand to execute on its vision. And it would be highly beneficial to the movement to take advantage of it. -
 On Free Speech On Free Speech2019 Apr 16 See all posts On Free Speech "A statement may be both true and dangerous. The previous sentence is such a statement." - David FriedmanFreedom of speech is a topic that many internet communities have struggled with over the last two decades. Cryptocurrency and blockchain communities, a major part of their raison d'etre being censorship resistance, are especially poised to value free speech very highly, and yet, over the last few years, the extremely rapid growth of these communities and the very high financial and social stakes involved have repeatedly tested the application and the limits of the concept. In this post, I aim to disentangle some of the contradictions, and make a case what the norm of "free speech" really stands for."Free speech laws" vs "free speech"A common, and in my own view frustrating, argument that I often hear is that "freedom of speech" is exclusively a legal restriction on what governments can act against, and has nothing to say regarding the actions of private entities such as corporations, privately-owned platforms, internet forums and conferences. One of the larger examples of "private censorship" in cryptocurrency communities was the decision of Theymos, the moderator of the /r/bitcoin subreddit, to start heavily moderating the subreddit, forbidding arguments in favor of increasing the Bitcoin blockchain's transaction capacity via a hard fork. Here is a timeline of the censorship as catalogued by John Blocke: https://medium.com/johnblocke/a-brief-and-incomplete-history-of-censorship-in-r-bitcoin-c85a290fe43Here is Theymos's post defending his policies: https://www.reddit.com/r/Bitcoin/comments/3h9cq4/its_time_for_a_break_about_the_recent_mess/, including the now infamous line "If 90% of /r/Bitcoin users find these policies to be intolerable, then I want these 90% of /r/Bitcoin users to leave".A common strategy used by defenders of Theymos's censorship was to say that heavy-handed moderation is okay because /r/bitcoin is "a private forum" owned by Theymos, and so he has the right to do whatever he wants in it; those who dislike it should move to other forums: And it's true that Theymos has not broken any laws by moderating his forum in this way. But to most people, it's clear that there is still some kind of free speech violation going on. So what gives? First of all, it's crucially important to recognize that freedom of speech is not just a law in some countries. It's also a social principle. And the underlying goal of the social principle is the same as the underlying goal of the law: to foster an environment where the ideas that win are ideas that are good, rather than just ideas that happen to be favored by people in a position of power. And governmental power is not the only kind of power that we need to protect from; there is also a corporation's power to fire someone, an internet forum moderator's power to delete almost every post in a discussion thread, and many other kinds of power hard and soft.So what is the underlying social principle here? Quoting Eliezer Yudkowsky:There are a very few injunctions in the human art of rationality that have no ifs, ands, buts, or escape clauses. This is one of them. Bad argument gets counterargument. Does not get bullet. Never. Never ever never for ever.Slatestarcodex elaborates:What does "bullet" mean in the quote above? Are other projectiles covered? Arrows? Boulders launched from catapults? What about melee weapons like swords or maces? Where exactly do we draw the line for "inappropriate responses to an argument"? A good response to an argument is one that addresses an idea; a bad argument is one that silences it. If you try to address an idea, your success depends on how good the idea is; if you try to silence it, your success depends on how powerful you are and how many pitchforks and torches you can provide on short notice. Shooting bullets is a good way to silence an idea without addressing it. So is firing stones from catapults, or slicing people open with swords, or gathering a pitchfork-wielding mob. But trying to get someone fired for holding an idea is also a way of silencing an idea without addressing it.That said, sometimes there is a rationale for "safe spaces" where people who, for whatever reason, just don't want to deal with arguments of a particular type, can congregate and where those arguments actually do get silenced. Perhaps the most innocuous of all is spaces like ethresear.ch where posts get silenced just for being "off topic" to keep the discussion focused. But there's also a dark side to the concept of "safe spaces"; as Ken White writes:This may come as a surprise, but I'm a supporter of ‘safe spaces.' I support safe spaces because I support freedom of association. Safe spaces, if designed in a principled way, are just an application of that freedom... But not everyone imagines "safe spaces" like that. Some use the concept of "safe spaces" as a sword, wielded to annex public spaces and demand that people within those spaces conform to their private norms. That's not freedom of associationAha. So making your own safe space off in a corner is totally fine, but there is also this concept of a "public space", and trying to turn a public space into a safe space for one particular special interest is wrong. So what is a "public space"? It's definitely clear that a public space is not just "a space owned and/or run by a government"; the concept of privately owned public spaces is a well-established one. This is true even informally: it's a common moral intuition, for example, that it's less bad for a private individual to commit violations such as discriminating against races and genders than it is for, say, a shopping mall to do the same. In the case or the /r/bitcoin subreddit, one can make the case, regardless of who technically owns the top moderator position in the subreddit, that the subreddit very much is a public space. A few arguments particularly stand out:It occupies "prime real estate", specifically the word "bitcoin", which makes people consider it to be the default place to discuss Bitcoin. The value of the space was created not just by Theymos, but by thousands of people who arrived on the subreddit to discuss Bitcoin with an implicit expectation that it is, and will continue, to be a public space for discussing Bitcoin. Theymos's shift in policy was a surprise to many people, and it was not foreseeable ahead of time that it would take place. If, instead, Theymos had created a subreddit called /r/bitcoinsmallblockers, and explicitly said that it was a curated space for small block proponents and attempting to instigate controversial hard forks was not welcome, then it seems likely that very few people would have seen anything wrong about this. They would have opposed his ideology, but few (at least in blockchain communities) would try to claim that it's improper for people with ideologies opposed to their own to have spaces for internal discussion. But back in reality, Theymos tried to "annex a public space and demand that people within the space confirm to his private norms", and so we have the Bitcoin community block size schism, a highly acrimonious fork and chain split, and now a cold peace between Bitcoin and Bitcoin Cash.DeplatformingAbout a year ago at Deconomy I publicly shouted down Craig Wright, a scammer claiming to be Satoshi Nakamoto, finishing my explanation of why the things he says make no sense with the question "why is this fraud allowed to speak at this conference?" Of course, Craig Wright's partisans replied back with.... accusations of censorship: Did I try to "silence" Craig Wright? I would argue, no. One could argue that this is because "Deconomy is not a public space", but I think the much better argument is that a conference is fundamentally different from an internet forum. An internet forum can actually try to be a fully neutral medium for discussion where anything goes; a conference, on the other hand, is by its very nature a highly curated list of presentations, allocating a limited number of speaking slots and actively channeling a large amount of attention to those lucky enough to get a chance to speak. A conference is an editorial act by the organizers, saying "here are some ideas and views that we think people really should be exposed to and hear". Every conference "censors" almost every viewpoint because there's not enough space to give them all a chance to speak, and this is inherent to the format; so raising an objection to a conference's judgement in making its selections is absolutely a legitimate act.This extends to other kinds of selective platforms. Online platforms such as Facebook, Twitter and Youtube already engage in active selection through algorithms that influence what people are more likely to be recommended. Typically, they do this for selfish reasons, setting up their algorithms to maximize "engagement" with their platform, often with unintended byproducts like promoting flat earth conspiracy theories. So given that these platforms are already engaging in (automated) selective presentation, it seems eminently reasonable to criticize them for not directing these same levers toward more pro-social objectives, or at the least pro-social objectives that all major reasonable political tribes agree on (eg. quality intellectual discourse). Additionally, the "censorship" doesn't seriously block anyone's ability to learn Craig Wright's side of the story; you can just go visit their website, here you go: https://coingeek.com/. If someone is already operating a platform that makes editorial decisions, asking them to make such decisions with the same magnitude but with more pro-social criteria seems like a very reasonable thing to do.A more recent example of this principle at work is the #DelistBSV campaign, where some cryptocurrency exchanges, most famously Binance, removed support for trading BSV (the Bitcoin fork promoted by Craig Weight). Once again, many people, even reasonable people, accused this campaign of being an exercise in censorship, raising parallels to credit card companies blocking Wikileaks: I personally have been a critic of the power wielded by centralized exchanges. Should I oppose #DelistBSV on free speech grounds? I would argue no, it's ok to support it, but this is definitely a much closer call.Many #DelistBSV participants like Kraken are definitely not "anything-goes" platforms; they already make many editorial decisions about which currencies they accept and refuse. Kraken only accepts about a dozen currencies, so they are passively "censoring" almost everyone. Shapeshift supports more currencies but it does not support SPANK, or even KNC. So in these two cases, delisting BSV is more like reallocation of a scarce resource (attention/legitimacy) than it is censorship. Binance is a bit different; it does accept a very large array of cryptocurrencies, adopting a philosophy much closer to anything-goes, and it does have a unique position as market leader with a lot of liquidity.That said, one can argue two things in Binance's favor. First of all, censorship is retaliating against a truly malicious exercise of censorship on the part of core BSV community members when they threatened critics like Peter McCormack with legal letters (see Peter's response); in "anarchic" environments with large disagreements on what the norms are, "an eye for an eye" in-kind retaliation is one of the better social norms to have because it ensures that people only face punishments that they in some sense have through their own actions demonstrated they believe are legitimate. Furthermore, the delistings won't make it that hard for people to buy or sell BSV; Coinex has said that they will not delist (and I would actually oppose second-tier "anything-goes" exchanges delisting). But the delistings do send a strong message of social condemnation of BSV, which is useful and needed. So there's a case to support all delistings so far, though on reflection Binance refusing to delist "because freedom" would have also been not as unreasonable as it seems at first glance.It's in general absolutely potentially reasonable to oppose the existence of a concentration of power, but support that concentration of power being used for purposes that you consider prosocial as long as that concentration exists; see Bryan Caplan's exposition on reconciling supporting open borders and also supporting anti-ebola restrictions for an example in a different field. Opposing concentrations of power only requires that one believe those concentrations of power to be on balance harmful and abusive; it does not mean that one must oppose all things that those concentrations of power do.If someone manages to make a completely permissionless cross-chain decentralized exchange that facilitates trade between any asset and any other asset, then being "listed" on the exchange would not send a social signal, because everyone is listed; and I would support such an exchange existing even if it supports trading BSV. The thing that I do support is BSV being removed from already exclusive positions that confer higher tiers of legitimacy than simple existence.So to conclude: censorship in public spaces bad, even if the public spaces are non-governmental; censorship in genuinely private spaces (especially spaces that are not "defaults" for a broader community) can be okay; ostracizing projects with the goal and effect of denying access to them, bad; ostracizing projects with the goal and effect of denying them scarce legitimacy can be okay.
On Free Speech On Free Speech2019 Apr 16 See all posts On Free Speech "A statement may be both true and dangerous. The previous sentence is such a statement." - David FriedmanFreedom of speech is a topic that many internet communities have struggled with over the last two decades. Cryptocurrency and blockchain communities, a major part of their raison d'etre being censorship resistance, are especially poised to value free speech very highly, and yet, over the last few years, the extremely rapid growth of these communities and the very high financial and social stakes involved have repeatedly tested the application and the limits of the concept. In this post, I aim to disentangle some of the contradictions, and make a case what the norm of "free speech" really stands for."Free speech laws" vs "free speech"A common, and in my own view frustrating, argument that I often hear is that "freedom of speech" is exclusively a legal restriction on what governments can act against, and has nothing to say regarding the actions of private entities such as corporations, privately-owned platforms, internet forums and conferences. One of the larger examples of "private censorship" in cryptocurrency communities was the decision of Theymos, the moderator of the /r/bitcoin subreddit, to start heavily moderating the subreddit, forbidding arguments in favor of increasing the Bitcoin blockchain's transaction capacity via a hard fork. Here is a timeline of the censorship as catalogued by John Blocke: https://medium.com/johnblocke/a-brief-and-incomplete-history-of-censorship-in-r-bitcoin-c85a290fe43Here is Theymos's post defending his policies: https://www.reddit.com/r/Bitcoin/comments/3h9cq4/its_time_for_a_break_about_the_recent_mess/, including the now infamous line "If 90% of /r/Bitcoin users find these policies to be intolerable, then I want these 90% of /r/Bitcoin users to leave".A common strategy used by defenders of Theymos's censorship was to say that heavy-handed moderation is okay because /r/bitcoin is "a private forum" owned by Theymos, and so he has the right to do whatever he wants in it; those who dislike it should move to other forums: And it's true that Theymos has not broken any laws by moderating his forum in this way. But to most people, it's clear that there is still some kind of free speech violation going on. So what gives? First of all, it's crucially important to recognize that freedom of speech is not just a law in some countries. It's also a social principle. And the underlying goal of the social principle is the same as the underlying goal of the law: to foster an environment where the ideas that win are ideas that are good, rather than just ideas that happen to be favored by people in a position of power. And governmental power is not the only kind of power that we need to protect from; there is also a corporation's power to fire someone, an internet forum moderator's power to delete almost every post in a discussion thread, and many other kinds of power hard and soft.So what is the underlying social principle here? Quoting Eliezer Yudkowsky:There are a very few injunctions in the human art of rationality that have no ifs, ands, buts, or escape clauses. This is one of them. Bad argument gets counterargument. Does not get bullet. Never. Never ever never for ever.Slatestarcodex elaborates:What does "bullet" mean in the quote above? Are other projectiles covered? Arrows? Boulders launched from catapults? What about melee weapons like swords or maces? Where exactly do we draw the line for "inappropriate responses to an argument"? A good response to an argument is one that addresses an idea; a bad argument is one that silences it. If you try to address an idea, your success depends on how good the idea is; if you try to silence it, your success depends on how powerful you are and how many pitchforks and torches you can provide on short notice. Shooting bullets is a good way to silence an idea without addressing it. So is firing stones from catapults, or slicing people open with swords, or gathering a pitchfork-wielding mob. But trying to get someone fired for holding an idea is also a way of silencing an idea without addressing it.That said, sometimes there is a rationale for "safe spaces" where people who, for whatever reason, just don't want to deal with arguments of a particular type, can congregate and where those arguments actually do get silenced. Perhaps the most innocuous of all is spaces like ethresear.ch where posts get silenced just for being "off topic" to keep the discussion focused. But there's also a dark side to the concept of "safe spaces"; as Ken White writes:This may come as a surprise, but I'm a supporter of ‘safe spaces.' I support safe spaces because I support freedom of association. Safe spaces, if designed in a principled way, are just an application of that freedom... But not everyone imagines "safe spaces" like that. Some use the concept of "safe spaces" as a sword, wielded to annex public spaces and demand that people within those spaces conform to their private norms. That's not freedom of associationAha. So making your own safe space off in a corner is totally fine, but there is also this concept of a "public space", and trying to turn a public space into a safe space for one particular special interest is wrong. So what is a "public space"? It's definitely clear that a public space is not just "a space owned and/or run by a government"; the concept of privately owned public spaces is a well-established one. This is true even informally: it's a common moral intuition, for example, that it's less bad for a private individual to commit violations such as discriminating against races and genders than it is for, say, a shopping mall to do the same. In the case or the /r/bitcoin subreddit, one can make the case, regardless of who technically owns the top moderator position in the subreddit, that the subreddit very much is a public space. A few arguments particularly stand out:It occupies "prime real estate", specifically the word "bitcoin", which makes people consider it to be the default place to discuss Bitcoin. The value of the space was created not just by Theymos, but by thousands of people who arrived on the subreddit to discuss Bitcoin with an implicit expectation that it is, and will continue, to be a public space for discussing Bitcoin. Theymos's shift in policy was a surprise to many people, and it was not foreseeable ahead of time that it would take place. If, instead, Theymos had created a subreddit called /r/bitcoinsmallblockers, and explicitly said that it was a curated space for small block proponents and attempting to instigate controversial hard forks was not welcome, then it seems likely that very few people would have seen anything wrong about this. They would have opposed his ideology, but few (at least in blockchain communities) would try to claim that it's improper for people with ideologies opposed to their own to have spaces for internal discussion. But back in reality, Theymos tried to "annex a public space and demand that people within the space confirm to his private norms", and so we have the Bitcoin community block size schism, a highly acrimonious fork and chain split, and now a cold peace between Bitcoin and Bitcoin Cash.DeplatformingAbout a year ago at Deconomy I publicly shouted down Craig Wright, a scammer claiming to be Satoshi Nakamoto, finishing my explanation of why the things he says make no sense with the question "why is this fraud allowed to speak at this conference?" Of course, Craig Wright's partisans replied back with.... accusations of censorship: Did I try to "silence" Craig Wright? I would argue, no. One could argue that this is because "Deconomy is not a public space", but I think the much better argument is that a conference is fundamentally different from an internet forum. An internet forum can actually try to be a fully neutral medium for discussion where anything goes; a conference, on the other hand, is by its very nature a highly curated list of presentations, allocating a limited number of speaking slots and actively channeling a large amount of attention to those lucky enough to get a chance to speak. A conference is an editorial act by the organizers, saying "here are some ideas and views that we think people really should be exposed to and hear". Every conference "censors" almost every viewpoint because there's not enough space to give them all a chance to speak, and this is inherent to the format; so raising an objection to a conference's judgement in making its selections is absolutely a legitimate act.This extends to other kinds of selective platforms. Online platforms such as Facebook, Twitter and Youtube already engage in active selection through algorithms that influence what people are more likely to be recommended. Typically, they do this for selfish reasons, setting up their algorithms to maximize "engagement" with their platform, often with unintended byproducts like promoting flat earth conspiracy theories. So given that these platforms are already engaging in (automated) selective presentation, it seems eminently reasonable to criticize them for not directing these same levers toward more pro-social objectives, or at the least pro-social objectives that all major reasonable political tribes agree on (eg. quality intellectual discourse). Additionally, the "censorship" doesn't seriously block anyone's ability to learn Craig Wright's side of the story; you can just go visit their website, here you go: https://coingeek.com/. If someone is already operating a platform that makes editorial decisions, asking them to make such decisions with the same magnitude but with more pro-social criteria seems like a very reasonable thing to do.A more recent example of this principle at work is the #DelistBSV campaign, where some cryptocurrency exchanges, most famously Binance, removed support for trading BSV (the Bitcoin fork promoted by Craig Weight). Once again, many people, even reasonable people, accused this campaign of being an exercise in censorship, raising parallels to credit card companies blocking Wikileaks: I personally have been a critic of the power wielded by centralized exchanges. Should I oppose #DelistBSV on free speech grounds? I would argue no, it's ok to support it, but this is definitely a much closer call.Many #DelistBSV participants like Kraken are definitely not "anything-goes" platforms; they already make many editorial decisions about which currencies they accept and refuse. Kraken only accepts about a dozen currencies, so they are passively "censoring" almost everyone. Shapeshift supports more currencies but it does not support SPANK, or even KNC. So in these two cases, delisting BSV is more like reallocation of a scarce resource (attention/legitimacy) than it is censorship. Binance is a bit different; it does accept a very large array of cryptocurrencies, adopting a philosophy much closer to anything-goes, and it does have a unique position as market leader with a lot of liquidity.That said, one can argue two things in Binance's favor. First of all, censorship is retaliating against a truly malicious exercise of censorship on the part of core BSV community members when they threatened critics like Peter McCormack with legal letters (see Peter's response); in "anarchic" environments with large disagreements on what the norms are, "an eye for an eye" in-kind retaliation is one of the better social norms to have because it ensures that people only face punishments that they in some sense have through their own actions demonstrated they believe are legitimate. Furthermore, the delistings won't make it that hard for people to buy or sell BSV; Coinex has said that they will not delist (and I would actually oppose second-tier "anything-goes" exchanges delisting). But the delistings do send a strong message of social condemnation of BSV, which is useful and needed. So there's a case to support all delistings so far, though on reflection Binance refusing to delist "because freedom" would have also been not as unreasonable as it seems at first glance.It's in general absolutely potentially reasonable to oppose the existence of a concentration of power, but support that concentration of power being used for purposes that you consider prosocial as long as that concentration exists; see Bryan Caplan's exposition on reconciling supporting open borders and also supporting anti-ebola restrictions for an example in a different field. Opposing concentrations of power only requires that one believe those concentrations of power to be on balance harmful and abusive; it does not mean that one must oppose all things that those concentrations of power do.If someone manages to make a completely permissionless cross-chain decentralized exchange that facilitates trade between any asset and any other asset, then being "listed" on the exchange would not send a social signal, because everyone is listed; and I would support such an exchange existing even if it supports trading BSV. The thing that I do support is BSV being removed from already exclusive positions that confer higher tiers of legitimacy than simple existence.So to conclude: censorship in public spaces bad, even if the public spaces are non-governmental; censorship in genuinely private spaces (especially spaces that are not "defaults" for a broader community) can be okay; ostracizing projects with the goal and effect of denying access to them, bad; ostracizing projects with the goal and effect of denying them scarce legitimacy can be okay. -
 On Collusion On Collusion2019 Apr 03 See all posts On Collusion Special thanks to Glen Weyl, Phil Daian and Jinglan Wang for reviewOver the last few years there has been an increasing interest in using deliberately engineered economic incentives and mechanism design to align behavior of participants in various contexts. In the blockchain space, mechanism design first and foremost provides the security for the blockchain itself, encouraging miners or proof of stake validators to participate honestly, but more recently it is being applied in prediction markets, "token curated registries" and many other contexts. The nascent RadicalXChange movement has meanwhile spawned experimentation with Harberger taxes, quadratic voting, quadratic financing and more. More recently, there has also been growing interest in using token-based incentives to try to encourage quality posts in social media. However, as development of these systems moves closer from theory to practice, there are a number of challenges that need to be addressed, challenges that I would argue have not yet been adequately confronted.As a recent example of this move from theory toward deployment, Bihu, a Chinese platform that has recently released a coin-based mechanism for encouraging people to write posts. The basic mechanism (see whitepaper in Chinese here) is that if a user of the platform holds KEY tokens, they have the ability to stake those KEY tokens on articles; every user can make \(k\) "upvotes" per day, and the "weight" of each upvote is proportional to the stake of the user making the upvote. Articles with a greater quantity of stake upvoting them appear more prominently, and the author of an article gets a reward of KEY tokens roughly proportional to the quantity of KEY upvoting that article. This is an oversimplification and the actual mechanism has some nonlinearities baked into it, but they are not essential to the basic functioning of the mechanism. KEY has value because it can be used in various ways inside the platform, but particularly a percentage of all ad revenues get used to buy and burn KEY (yay, big thumbs up to them for doing this and not making yet another medium of exchange token!).This kind of design is far from unique; incentivizing online content creation is something that very many people care about, and there have been many designs of a similar character, as well as some fairly different designs. And in this case this particular platform is already being used significantly: A few months ago, the Ethereum trading subreddit /r/ethtrader introduced a somewhat similar experimental feature where a token called "donuts" is issued to users that make comments that get upvoted, with a set amount of donuts issued weekly to users in proportion to how many upvotes their comments received. The donuts could be used to buy the right to set the contents of the banner at the top of the subreddit, and could also be used to vote in community polls. However, unlike what happens in the KEY system, here the reward that B receives when A upvotes B is not proportional to A's existing coin supply; instead, each Reddit account has an equal ability to contribute to other Reddit accounts. These kinds of experiments, attempting to reward quality content creation in a way that goes beyond the known limitations of donations/microtipping, are very valuable; under-compensation of user-generated internet content is a very significant problem in society in general (see "liberal radicalism" and "data as labor"), and it's heartening to see crypto communities attempting to use the power of mechanism design to make inroads on solving it. But unfortunately, these systems are also vulnerable to attack.Self-voting, plutocracy and bribesHere is how one might economically attack the design proposed above. Suppose that some wealthy user acquires some quantity \(N\) of tokens, and as a result each of the user's \(k\) upvotes gives the recipient a reward of \(N \cdot q\) (\(q\) here probably being a very small number, eg. think \(q = 0.000001\)). The user simply upvotes their own sockpuppet accounts, giving themselves the reward of \(N \cdot k \cdot q\). Then, the system simply collapses into each user having an "interest rate" of \(k \cdot q\) per period, and the mechanism accomplishes nothing else.The actual Bihu mechanism seemed to anticipate this, and has some superlinear logic where articles with more KEY upvoting them gain a disproportionately greater reward, seemingly to encourage upvoting popular posts rather than self-upvoting. It's a common pattern among coin voting governance systems to add this kind of superlinearity to prevent self-voting from undermining the entire system; most DPOS schemes have a limited number of delegate slots with zero rewards for anyone who does not get enough votes to join one of the slots, with similar effect. But these schemes invariably introduce two new weaknesses:They subsidize plutocracy, as very wealthy individuals and cartels can still get enough funds to self-upvote. They can be circumvented by users bribing other users to vote for them en masse. Bribing attacks may sound farfetched (who here has ever accepted a bribe in real life?), but in a mature ecosystem they are much more realistic than they seem. In most contexts where bribing has taken place in the blockchain space, the operators use a euphemistic new name to give the concept a friendly face: it's not a bribe, it's a "staking pool" that "shares dividends". Bribes can even be obfuscated: imagine a cryptocurrency exchange that offers zero fees and spends the effort to make an abnormally good user interface, and does not even try to collect a profit; instead, it uses coins that users deposit to participate in various coin voting systems. There will also inevitably be people that see in-group collusion as just plain normal; see a recent scandal involving EOS DPOS for one example: Finally, there is the possibility of a "negative bribe", ie. blackmail or coercion, threatening participants with harm unless they act inside the mechanism in a certain way.In the /r/ethtrader experiment, fear of people coming in and buying donuts to shift governance polls led to the community deciding to make only locked (ie. untradeable) donuts eligible for use in voting. But there's an even cheaper attack than buying donuts (an attack that can be thought of as a kind of obfuscated bribe): renting them. If an attacker is already holding ETH, they can use it as collateral on a platform like Compound to take out a loan of some token, giving you the full right to use that token for whatever purpose including participating in votes, and when they're done they simply send the tokens back to the loan contract to get their collateral back - all without having to endure even a second of price exposure to the token that they just used to swing a coin vote, even if the coin vote mechanism includes a time lockup (as eg. Bihu does). In every case, issues around bribing, and accidentally over-empowering well-connected and wealthy participants, prove surprisingly difficult to avoid.IdentitySome systems attempt to mitigate the plutocratic aspects of coin voting by making use of an identity system. In the case of the /r/ethtrader donut system, for example, although governance polls are done via coin vote, the mechanism that determines how many donuts (ie. coins) you get in the first place is based on Reddit accounts: 1 upvote from 1 Reddit account = \(N\) donuts earned. The ideal goal of an identity system is to make it relatively easy for individuals to get one identity, but relatively difficult to get many identities. In the /r/ethtrader donut system, that's Reddit accounts, in the Gitcoin CLR matching gadget, it's Github accounts that are used for the same purpose. But identity, at least the way it has been implemented so far, is a fragile thing.... Oh, are you too lazy to make a big rack of phones? Well maybe you're looking for this: Usual warning about how sketchy sites may or may not scam you, do your own research, etc. etc. applies.Arguably, attacking these mechanisms by simply controlling thousands of fake identities like a puppetmaster is even easier than having to go through the trouble of bribing people. And if you think the response is to just increase security to go up to government-level IDs? Well, if you want to get a few of those you can start exploring here, but keep in mind that there are specialized criminal organizations that are well ahead of you, and even if all the underground ones are taken down, hostile governments are definitely going to create fake passports by the millions if we're stupid enough to create systems that make that sort of activity profitable. And this doesn't even begin to mention attacks in the opposite direction, identity-issuing institutions attempting to disempower marginalized communities by denying them identity documents...CollusionGiven that so many mechanisms seem to fail in such similar ways once multiple identities or even liquid markets get into the picture, one might ask, is there some deep common strand that causes all of these issues? I would argue the answer is yes, and the "common strand" is this: it is much harder, and more likely to be outright impossible, to make mechanisms that maintain desirable properties in a model where participants can collude, than in a model where they can't. Most people likely already have some intuition about this; specific instances of this principle are behind well-established norms and often laws promoting competitive markets and restricting price-fixing cartels, vote buying and selling, and bribery. But the issue is much deeper and more general.In the version of game theory that focuses on individual choice - that is, the version that assumes that each participant makes decisions independently and that does not allow for the possibility of groups of agents working as one for their mutual benefit, there are mathematical proofs that at least one stable Nash equilibrium must exist in any game, and mechanism designers have a very wide latitude to "engineer" games to achieve specific outcomes. But in the version of game theory that allows for the possibility of coalitions working together, called cooperative game theory, there are large classes of games that do not have any stable outcome that a coalition cannot profitably deviate from.Majority games, formally described as games of \(N\) agents where any subset of more than half of them can capture a fixed reward and split it among themselves, a setup eerily similar to many situations in corporate governance, politics and many other situations in human life, are part of that set of inherently unstable games. That is to say, if there is a situation with some fixed pool of resources and some currently established mechanism for distributing those resources, and it's unavoidably possible for 51% of the participants can conspire to seize control of the resources, no matter what the current configuration is there is always some conspiracy that can emerge that would be profitable for the participants. However, that conspiracy would then in turn be vulnerable to potential new conspiracies, possibly including a combination of previous conspirators and victims... and so on and so forth. Round A B C 1 1/3 1/3 1/3 2 1/2 1/2 0 3 2/3 0 1/3 4 0 1/3 2/3 This fact, the instability of majority games under cooperative game theory, is arguably highly underrated as a simplified general mathematical model of why there may well be no "end of history" in politics and no system that proves fully satisfactory; I personally believe it's much more useful than the more famous Arrow's theorem, for example.There are two ways to get around this issue. The first is to try to restrict ourselves to the class of games that are "identity-free" and "collusion-safe", so where we do not need to worry about either bribes or identities. The second is to try to attack the identity and collusion resistance problems directly, and actually solve them well enough that we can implement non-collusion-safe games with the richer properties that they offer.Identity-free and collusion-safe game designThe class of games that is identity-free and collusion-safe is substantial. Even proof of work is collusion-safe up to the bound of a single actor having ~23.21% of total hashpower, and this bound can be increased up to 50% with clever engineering. Competitive markets are reasonably collusion-safe up until a relatively high bound, which is easily reached in some cases but in other cases is not.In the case of governance and content curation (both of which are really just special cases of the general problem of identifying public goods and public bads) a major class of mechanism that works well is futarchy - typically portrayed as "governance by prediction market", though I would also argue that the use of security deposits is fundamentally in the same class of technique. The way futarchy mechanisms, in their most general form, work is that they make "voting" not just an expression of opinion, but also a prediction, with a reward for making predictions that are true and a penalty for making predictions that are false. For example, my proposal for "prediction markets for content curation DAOs" suggests a semi-centralized design where anyone can upvote or downvote submitted content, with content that is upvoted more being more visible, where there is also a "moderation panel" that makes final decisions. For each post, there is a small probability (proportional to the total volume of upvotes+downvotes on that post) that the moderation panel will be called on to make a final decision on the post. If the moderation panel approves a post, everyone who upvoted it is rewarded and everyone who downvoted it is penalized, and if the moderation panel disapproves a post the reverse happens; this mechanism encourages participants to make upvotes and downvotes that try to "predict" the moderation panel's judgements.Another possible example of futarchy is a governance system for a project with a token, where anyone who votes for a decision is obligated to purchase some quantity of tokens at the price at the time the vote begins if the vote wins; this ensures that voting on a bad decision is costly, and in the limit if a bad decision wins a vote everyone who approved the decision must essentially buy out everyone else in the project. This ensures that an individual vote for a "wrong" decision can be very costly for the voter, precluding the possibility of cheap bribe attacks. A graphical description of one form of futarchy, creating two markets representing the two "possible future worlds" and picking the one with a more favorable price. Source this post on ethresear.chHowever, that range of things that mechanisms of this type can do is limited. In the case of the content curation example above, we're not really solving governance, we're just scaling the functionality of a governance gadget that is already assumed to be trusted. One could try to replace the moderation panel with a prediction market on the price of a token representing the right to purchase advertising space, but in practice prices are too noisy an indicator to make this viable for anything but a very small number of very large decisions. And often the value that we're trying to maximize is explicitly something other than maximum value of a coin.Let's take a more explicit look at why, in the more general case where we can't easily determine the value of a governance decision via its impact on the price of a token, good mechanisms for identifying public goods and bads unfortunately cannot be identity-free or collusion-safe. If one tries to preserve the property of a game being identity-free, building a system where identities don't matter and only coins do, there is an impossible tradeoff between either failing to incentivize legitimate public goods or over-subsidizing plutocracy.The argument is as follows. Suppose that there is some author that is producing a public good (eg. a series of blog posts) that provides value to each member of a community of 10000 people. Suppose there exists some mechanism where members of the community can take an action that causes the author to receive a gain of $1. Unless the community members are extremely altruistic, for the mechanism to work the cost of taking this action must be much lower than $1, as otherwise the portion of the benefit captured by the member of the community supporting the author would be much smaller than the cost of supporting the author, and so the system collapses into a tragedy of the commons where no one supports the author. Hence, there must exist a way to cause the author to earn $1 at a cost much less than $1. But now suppose that there is also a fake community, which consists of 10000 fake sockpuppet accounts of the same wealthy attacker. This community takes all of the same actions as the real community, except instead of supporting the author, they support another fake account which is also a sockpuppet of the attacker. If it was possible for a member of the "real community" to give the author $1 at a personal cost of much less than $1, it's possible for the attacker to give themselves $1 at a cost much less than $1 over and over again, and thereby drain the system's funding. Any mechanism that can help genuinely under-coordinated parties coordinate will, without the right safeguards, also help already coordinated parties (such as many accounts controlled by the same person) over-coordinate, extracting money from the system.A similar challenge arises when the goal is not funding, but rather determining what content should be most visible. What content do you think would get more dollar value supporting it: a legitimately high quality blog article benefiting thousands of people but benefiting each individual person relatively slightly, or this? Or perhaps this? Those who have been following recent politics "in the real world" might also point out a different kind of content that benefits highly centralized actors: social media manipulation by hostile governments. Ultimately, both centralized systems and decentralized systems are facing the same fundamental problem, which is that the "marketplace of ideas" (and of public goods more generally) is very far from an "efficient market" in the sense that economists normally use the term, and this leads to both underproduction of public goods even in "peacetime" but also vulnerability to active attacks. It's just a hard problem.This is also why coin-based voting systems (like Bihu's) have one major genuine advantage over identity-based systems (like the Gitcoin CLR or the /r/ethtrader donut experiment): at least there is no benefit to buying accounts en masse, because everything you do is proportional to how many coins you have, regardless of how many accounts the coins are split between. However, mechanisms that do not rely on any model of identity and only rely on coins fundamentally cannot solve the problem of concentrated interests outcompeting dispersed communities trying to support public goods; an identity-free mechanism that empowers distributed communities cannot avoid over-empowering centralized plutocrats pretending to be distributed communities.But it's not just identity issues that public goods games are vulnerable too; it's also bribes. To see why, consider again the example above, but where instead of the "fake community" being 10001 sockpuppets of the attacker, the attacker only has one identity, the account receiving funding, and the other 10000 accounts are real users - but users that receive a bribe of $0.01 each to take the action that would cause the attacker to gain an additional $1. As mentioned above, these bribes can be highly obfuscated, even through third-party custodial services that vote on a user's behalf in exchange for convenience, and in the case of "coin vote" designs an obfuscated bribe is even easier: one can do it by renting coins on the market and using them to participate in votes. Hence, while some kinds of games, particularly prediction market or security deposit based games, can be made collusion-safe and identity-free, generalized public goods funding seems to be a class of problem where collusion-safe and identity-free approaches unfortunately just cannot be made to work.Collusion resistance and identityThe other alternative is attacking the identity problem head-on. As mentioned above, simply going up to higher-security centralized identity systems, like passports and other government IDs, will not work at scale; in a sufficiently incentivized context, they are very insecure and vulnerable to the issuing governments themselves! Rather, the kind of "identity" we are talking about here is some kind of robust multifactorial set of claims that an actor identified by some set of messages actually is a unique individual. A very early proto-model of this kind of networked identity is arguably social recovery in HTC's blockchain phone: The basic idea is that your private key is secret-shared between up to five trusted contacts, in such a way that mathematically ensures that three of them can recover the original key, but two or fewer can't. This qualifies as an "identity system" - it's your five friends determining whether or not someone trying to recover your account actually is you. However, it's a special-purpose identity system trying to solve a problem - personal account security - that is different from (and easier than!) the problem of attempting to identify unique humans. That said, the general model of individuals making claims about each other can quite possibly be bootstrapped into some kind of more robust identity model. These systems could be augmented if desired using the "futarchy" mechanic described above: if someone makes a claim that someone is a unique human, and someone else disagrees, and both sides are willing to put down a bond to litigate the issue, the system can call together a judgement panel to determine who is right.But we also want another crucially important property: we want an identity that you cannot credibly rent or sell. Obviously, we can't prevent people from making a deal "you send me $50, I'll send you my key", but what we can try to do is prevent such deals from being credible - make it so that the seller can easily cheat the buyer and give the buyer a key that doesn't actually work. One way to do this is to make a mechanism by which the owner of a key can send a transaction that revokes the key and replaces it with another key of the owner's choice, all in a way that cannot be proven. Perhaps the simplest way to get around this is to either use a trusted party that runs the computation and only publishes results (along with zero knowledge proofs proving the results, so the trusted party is trusted only for privacy, not integrity), or decentralize the same functionality through multi-party computation. Such approaches will not solve collusion completely; a group of friends could still come together and sit on the same couch and coordinate votes, but they will at least reduce it to a manageable extent that will not lead to these systems outright failing.There is a further problem: initial distribution of the key. What happens if a user creates their identity inside a third-party custodial service that then stores the private key and uses it to clandestinely make votes on things? This would be an implicit bribe, the user's voting power in exchange for providing to the user a convenient service, and what's more, if the system is secure in that it successfully prevents bribes by making votes unprovable, clandestine voting by third-party hosts would also be undetectable. The only approach that gets around this problem seems to be.... in-person verification. For example, one could have an ecosystem of "issuers" where each issuer issues smart cards with private keys, which the user can immediately download onto their smartphone and send a message to replace the key with a different key that they do not reveal to anyone. These issuers could be meetups and conferences, or potentially individuals that have already been deemed by some voting mechanic to be trustworthy.Building out the infrastructure for making collusion-resistant mechanisms possible, including robust decentralized identity systems, is a difficult challenge, but if we want to unlock the potential of such mechanisms, it seems unavoidable that we have to do our best to try. It is true that the current computer-security dogma around, for example, introducing online voting is simply "don't", but if we want to expand the role of voting-like mechanisms, including more advanced forms such as quadratic voting and quadratic finance, to more roles, we have no choice but to confront the challenge head-on, try really hard, and hopefully succeed at making something secure enough, for at least some use cases.
On Collusion On Collusion2019 Apr 03 See all posts On Collusion Special thanks to Glen Weyl, Phil Daian and Jinglan Wang for reviewOver the last few years there has been an increasing interest in using deliberately engineered economic incentives and mechanism design to align behavior of participants in various contexts. In the blockchain space, mechanism design first and foremost provides the security for the blockchain itself, encouraging miners or proof of stake validators to participate honestly, but more recently it is being applied in prediction markets, "token curated registries" and many other contexts. The nascent RadicalXChange movement has meanwhile spawned experimentation with Harberger taxes, quadratic voting, quadratic financing and more. More recently, there has also been growing interest in using token-based incentives to try to encourage quality posts in social media. However, as development of these systems moves closer from theory to practice, there are a number of challenges that need to be addressed, challenges that I would argue have not yet been adequately confronted.As a recent example of this move from theory toward deployment, Bihu, a Chinese platform that has recently released a coin-based mechanism for encouraging people to write posts. The basic mechanism (see whitepaper in Chinese here) is that if a user of the platform holds KEY tokens, they have the ability to stake those KEY tokens on articles; every user can make \(k\) "upvotes" per day, and the "weight" of each upvote is proportional to the stake of the user making the upvote. Articles with a greater quantity of stake upvoting them appear more prominently, and the author of an article gets a reward of KEY tokens roughly proportional to the quantity of KEY upvoting that article. This is an oversimplification and the actual mechanism has some nonlinearities baked into it, but they are not essential to the basic functioning of the mechanism. KEY has value because it can be used in various ways inside the platform, but particularly a percentage of all ad revenues get used to buy and burn KEY (yay, big thumbs up to them for doing this and not making yet another medium of exchange token!).This kind of design is far from unique; incentivizing online content creation is something that very many people care about, and there have been many designs of a similar character, as well as some fairly different designs. And in this case this particular platform is already being used significantly: A few months ago, the Ethereum trading subreddit /r/ethtrader introduced a somewhat similar experimental feature where a token called "donuts" is issued to users that make comments that get upvoted, with a set amount of donuts issued weekly to users in proportion to how many upvotes their comments received. The donuts could be used to buy the right to set the contents of the banner at the top of the subreddit, and could also be used to vote in community polls. However, unlike what happens in the KEY system, here the reward that B receives when A upvotes B is not proportional to A's existing coin supply; instead, each Reddit account has an equal ability to contribute to other Reddit accounts. These kinds of experiments, attempting to reward quality content creation in a way that goes beyond the known limitations of donations/microtipping, are very valuable; under-compensation of user-generated internet content is a very significant problem in society in general (see "liberal radicalism" and "data as labor"), and it's heartening to see crypto communities attempting to use the power of mechanism design to make inroads on solving it. But unfortunately, these systems are also vulnerable to attack.Self-voting, plutocracy and bribesHere is how one might economically attack the design proposed above. Suppose that some wealthy user acquires some quantity \(N\) of tokens, and as a result each of the user's \(k\) upvotes gives the recipient a reward of \(N \cdot q\) (\(q\) here probably being a very small number, eg. think \(q = 0.000001\)). The user simply upvotes their own sockpuppet accounts, giving themselves the reward of \(N \cdot k \cdot q\). Then, the system simply collapses into each user having an "interest rate" of \(k \cdot q\) per period, and the mechanism accomplishes nothing else.The actual Bihu mechanism seemed to anticipate this, and has some superlinear logic where articles with more KEY upvoting them gain a disproportionately greater reward, seemingly to encourage upvoting popular posts rather than self-upvoting. It's a common pattern among coin voting governance systems to add this kind of superlinearity to prevent self-voting from undermining the entire system; most DPOS schemes have a limited number of delegate slots with zero rewards for anyone who does not get enough votes to join one of the slots, with similar effect. But these schemes invariably introduce two new weaknesses:They subsidize plutocracy, as very wealthy individuals and cartels can still get enough funds to self-upvote. They can be circumvented by users bribing other users to vote for them en masse. Bribing attacks may sound farfetched (who here has ever accepted a bribe in real life?), but in a mature ecosystem they are much more realistic than they seem. In most contexts where bribing has taken place in the blockchain space, the operators use a euphemistic new name to give the concept a friendly face: it's not a bribe, it's a "staking pool" that "shares dividends". Bribes can even be obfuscated: imagine a cryptocurrency exchange that offers zero fees and spends the effort to make an abnormally good user interface, and does not even try to collect a profit; instead, it uses coins that users deposit to participate in various coin voting systems. There will also inevitably be people that see in-group collusion as just plain normal; see a recent scandal involving EOS DPOS for one example: Finally, there is the possibility of a "negative bribe", ie. blackmail or coercion, threatening participants with harm unless they act inside the mechanism in a certain way.In the /r/ethtrader experiment, fear of people coming in and buying donuts to shift governance polls led to the community deciding to make only locked (ie. untradeable) donuts eligible for use in voting. But there's an even cheaper attack than buying donuts (an attack that can be thought of as a kind of obfuscated bribe): renting them. If an attacker is already holding ETH, they can use it as collateral on a platform like Compound to take out a loan of some token, giving you the full right to use that token for whatever purpose including participating in votes, and when they're done they simply send the tokens back to the loan contract to get their collateral back - all without having to endure even a second of price exposure to the token that they just used to swing a coin vote, even if the coin vote mechanism includes a time lockup (as eg. Bihu does). In every case, issues around bribing, and accidentally over-empowering well-connected and wealthy participants, prove surprisingly difficult to avoid.IdentitySome systems attempt to mitigate the plutocratic aspects of coin voting by making use of an identity system. In the case of the /r/ethtrader donut system, for example, although governance polls are done via coin vote, the mechanism that determines how many donuts (ie. coins) you get in the first place is based on Reddit accounts: 1 upvote from 1 Reddit account = \(N\) donuts earned. The ideal goal of an identity system is to make it relatively easy for individuals to get one identity, but relatively difficult to get many identities. In the /r/ethtrader donut system, that's Reddit accounts, in the Gitcoin CLR matching gadget, it's Github accounts that are used for the same purpose. But identity, at least the way it has been implemented so far, is a fragile thing.... Oh, are you too lazy to make a big rack of phones? Well maybe you're looking for this: Usual warning about how sketchy sites may or may not scam you, do your own research, etc. etc. applies.Arguably, attacking these mechanisms by simply controlling thousands of fake identities like a puppetmaster is even easier than having to go through the trouble of bribing people. And if you think the response is to just increase security to go up to government-level IDs? Well, if you want to get a few of those you can start exploring here, but keep in mind that there are specialized criminal organizations that are well ahead of you, and even if all the underground ones are taken down, hostile governments are definitely going to create fake passports by the millions if we're stupid enough to create systems that make that sort of activity profitable. And this doesn't even begin to mention attacks in the opposite direction, identity-issuing institutions attempting to disempower marginalized communities by denying them identity documents...CollusionGiven that so many mechanisms seem to fail in such similar ways once multiple identities or even liquid markets get into the picture, one might ask, is there some deep common strand that causes all of these issues? I would argue the answer is yes, and the "common strand" is this: it is much harder, and more likely to be outright impossible, to make mechanisms that maintain desirable properties in a model where participants can collude, than in a model where they can't. Most people likely already have some intuition about this; specific instances of this principle are behind well-established norms and often laws promoting competitive markets and restricting price-fixing cartels, vote buying and selling, and bribery. But the issue is much deeper and more general.In the version of game theory that focuses on individual choice - that is, the version that assumes that each participant makes decisions independently and that does not allow for the possibility of groups of agents working as one for their mutual benefit, there are mathematical proofs that at least one stable Nash equilibrium must exist in any game, and mechanism designers have a very wide latitude to "engineer" games to achieve specific outcomes. But in the version of game theory that allows for the possibility of coalitions working together, called cooperative game theory, there are large classes of games that do not have any stable outcome that a coalition cannot profitably deviate from.Majority games, formally described as games of \(N\) agents where any subset of more than half of them can capture a fixed reward and split it among themselves, a setup eerily similar to many situations in corporate governance, politics and many other situations in human life, are part of that set of inherently unstable games. That is to say, if there is a situation with some fixed pool of resources and some currently established mechanism for distributing those resources, and it's unavoidably possible for 51% of the participants can conspire to seize control of the resources, no matter what the current configuration is there is always some conspiracy that can emerge that would be profitable for the participants. However, that conspiracy would then in turn be vulnerable to potential new conspiracies, possibly including a combination of previous conspirators and victims... and so on and so forth. Round A B C 1 1/3 1/3 1/3 2 1/2 1/2 0 3 2/3 0 1/3 4 0 1/3 2/3 This fact, the instability of majority games under cooperative game theory, is arguably highly underrated as a simplified general mathematical model of why there may well be no "end of history" in politics and no system that proves fully satisfactory; I personally believe it's much more useful than the more famous Arrow's theorem, for example.There are two ways to get around this issue. The first is to try to restrict ourselves to the class of games that are "identity-free" and "collusion-safe", so where we do not need to worry about either bribes or identities. The second is to try to attack the identity and collusion resistance problems directly, and actually solve them well enough that we can implement non-collusion-safe games with the richer properties that they offer.Identity-free and collusion-safe game designThe class of games that is identity-free and collusion-safe is substantial. Even proof of work is collusion-safe up to the bound of a single actor having ~23.21% of total hashpower, and this bound can be increased up to 50% with clever engineering. Competitive markets are reasonably collusion-safe up until a relatively high bound, which is easily reached in some cases but in other cases is not.In the case of governance and content curation (both of which are really just special cases of the general problem of identifying public goods and public bads) a major class of mechanism that works well is futarchy - typically portrayed as "governance by prediction market", though I would also argue that the use of security deposits is fundamentally in the same class of technique. The way futarchy mechanisms, in their most general form, work is that they make "voting" not just an expression of opinion, but also a prediction, with a reward for making predictions that are true and a penalty for making predictions that are false. For example, my proposal for "prediction markets for content curation DAOs" suggests a semi-centralized design where anyone can upvote or downvote submitted content, with content that is upvoted more being more visible, where there is also a "moderation panel" that makes final decisions. For each post, there is a small probability (proportional to the total volume of upvotes+downvotes on that post) that the moderation panel will be called on to make a final decision on the post. If the moderation panel approves a post, everyone who upvoted it is rewarded and everyone who downvoted it is penalized, and if the moderation panel disapproves a post the reverse happens; this mechanism encourages participants to make upvotes and downvotes that try to "predict" the moderation panel's judgements.Another possible example of futarchy is a governance system for a project with a token, where anyone who votes for a decision is obligated to purchase some quantity of tokens at the price at the time the vote begins if the vote wins; this ensures that voting on a bad decision is costly, and in the limit if a bad decision wins a vote everyone who approved the decision must essentially buy out everyone else in the project. This ensures that an individual vote for a "wrong" decision can be very costly for the voter, precluding the possibility of cheap bribe attacks. A graphical description of one form of futarchy, creating two markets representing the two "possible future worlds" and picking the one with a more favorable price. Source this post on ethresear.chHowever, that range of things that mechanisms of this type can do is limited. In the case of the content curation example above, we're not really solving governance, we're just scaling the functionality of a governance gadget that is already assumed to be trusted. One could try to replace the moderation panel with a prediction market on the price of a token representing the right to purchase advertising space, but in practice prices are too noisy an indicator to make this viable for anything but a very small number of very large decisions. And often the value that we're trying to maximize is explicitly something other than maximum value of a coin.Let's take a more explicit look at why, in the more general case where we can't easily determine the value of a governance decision via its impact on the price of a token, good mechanisms for identifying public goods and bads unfortunately cannot be identity-free or collusion-safe. If one tries to preserve the property of a game being identity-free, building a system where identities don't matter and only coins do, there is an impossible tradeoff between either failing to incentivize legitimate public goods or over-subsidizing plutocracy.The argument is as follows. Suppose that there is some author that is producing a public good (eg. a series of blog posts) that provides value to each member of a community of 10000 people. Suppose there exists some mechanism where members of the community can take an action that causes the author to receive a gain of $1. Unless the community members are extremely altruistic, for the mechanism to work the cost of taking this action must be much lower than $1, as otherwise the portion of the benefit captured by the member of the community supporting the author would be much smaller than the cost of supporting the author, and so the system collapses into a tragedy of the commons where no one supports the author. Hence, there must exist a way to cause the author to earn $1 at a cost much less than $1. But now suppose that there is also a fake community, which consists of 10000 fake sockpuppet accounts of the same wealthy attacker. This community takes all of the same actions as the real community, except instead of supporting the author, they support another fake account which is also a sockpuppet of the attacker. If it was possible for a member of the "real community" to give the author $1 at a personal cost of much less than $1, it's possible for the attacker to give themselves $1 at a cost much less than $1 over and over again, and thereby drain the system's funding. Any mechanism that can help genuinely under-coordinated parties coordinate will, without the right safeguards, also help already coordinated parties (such as many accounts controlled by the same person) over-coordinate, extracting money from the system.A similar challenge arises when the goal is not funding, but rather determining what content should be most visible. What content do you think would get more dollar value supporting it: a legitimately high quality blog article benefiting thousands of people but benefiting each individual person relatively slightly, or this? Or perhaps this? Those who have been following recent politics "in the real world" might also point out a different kind of content that benefits highly centralized actors: social media manipulation by hostile governments. Ultimately, both centralized systems and decentralized systems are facing the same fundamental problem, which is that the "marketplace of ideas" (and of public goods more generally) is very far from an "efficient market" in the sense that economists normally use the term, and this leads to both underproduction of public goods even in "peacetime" but also vulnerability to active attacks. It's just a hard problem.This is also why coin-based voting systems (like Bihu's) have one major genuine advantage over identity-based systems (like the Gitcoin CLR or the /r/ethtrader donut experiment): at least there is no benefit to buying accounts en masse, because everything you do is proportional to how many coins you have, regardless of how many accounts the coins are split between. However, mechanisms that do not rely on any model of identity and only rely on coins fundamentally cannot solve the problem of concentrated interests outcompeting dispersed communities trying to support public goods; an identity-free mechanism that empowers distributed communities cannot avoid over-empowering centralized plutocrats pretending to be distributed communities.But it's not just identity issues that public goods games are vulnerable too; it's also bribes. To see why, consider again the example above, but where instead of the "fake community" being 10001 sockpuppets of the attacker, the attacker only has one identity, the account receiving funding, and the other 10000 accounts are real users - but users that receive a bribe of $0.01 each to take the action that would cause the attacker to gain an additional $1. As mentioned above, these bribes can be highly obfuscated, even through third-party custodial services that vote on a user's behalf in exchange for convenience, and in the case of "coin vote" designs an obfuscated bribe is even easier: one can do it by renting coins on the market and using them to participate in votes. Hence, while some kinds of games, particularly prediction market or security deposit based games, can be made collusion-safe and identity-free, generalized public goods funding seems to be a class of problem where collusion-safe and identity-free approaches unfortunately just cannot be made to work.Collusion resistance and identityThe other alternative is attacking the identity problem head-on. As mentioned above, simply going up to higher-security centralized identity systems, like passports and other government IDs, will not work at scale; in a sufficiently incentivized context, they are very insecure and vulnerable to the issuing governments themselves! Rather, the kind of "identity" we are talking about here is some kind of robust multifactorial set of claims that an actor identified by some set of messages actually is a unique individual. A very early proto-model of this kind of networked identity is arguably social recovery in HTC's blockchain phone: The basic idea is that your private key is secret-shared between up to five trusted contacts, in such a way that mathematically ensures that three of them can recover the original key, but two or fewer can't. This qualifies as an "identity system" - it's your five friends determining whether or not someone trying to recover your account actually is you. However, it's a special-purpose identity system trying to solve a problem - personal account security - that is different from (and easier than!) the problem of attempting to identify unique humans. That said, the general model of individuals making claims about each other can quite possibly be bootstrapped into some kind of more robust identity model. These systems could be augmented if desired using the "futarchy" mechanic described above: if someone makes a claim that someone is a unique human, and someone else disagrees, and both sides are willing to put down a bond to litigate the issue, the system can call together a judgement panel to determine who is right.But we also want another crucially important property: we want an identity that you cannot credibly rent or sell. Obviously, we can't prevent people from making a deal "you send me $50, I'll send you my key", but what we can try to do is prevent such deals from being credible - make it so that the seller can easily cheat the buyer and give the buyer a key that doesn't actually work. One way to do this is to make a mechanism by which the owner of a key can send a transaction that revokes the key and replaces it with another key of the owner's choice, all in a way that cannot be proven. Perhaps the simplest way to get around this is to either use a trusted party that runs the computation and only publishes results (along with zero knowledge proofs proving the results, so the trusted party is trusted only for privacy, not integrity), or decentralize the same functionality through multi-party computation. Such approaches will not solve collusion completely; a group of friends could still come together and sit on the same couch and coordinate votes, but they will at least reduce it to a manageable extent that will not lead to these systems outright failing.There is a further problem: initial distribution of the key. What happens if a user creates their identity inside a third-party custodial service that then stores the private key and uses it to clandestinely make votes on things? This would be an implicit bribe, the user's voting power in exchange for providing to the user a convenient service, and what's more, if the system is secure in that it successfully prevents bribes by making votes unprovable, clandestine voting by third-party hosts would also be undetectable. The only approach that gets around this problem seems to be.... in-person verification. For example, one could have an ecosystem of "issuers" where each issuer issues smart cards with private keys, which the user can immediately download onto their smartphone and send a message to replace the key with a different key that they do not reveal to anyone. These issuers could be meetups and conferences, or potentially individuals that have already been deemed by some voting mechanic to be trustworthy.Building out the infrastructure for making collusion-resistant mechanisms possible, including robust decentralized identity systems, is a difficult challenge, but if we want to unlock the potential of such mechanisms, it seems unavoidable that we have to do our best to try. It is true that the current computer-security dogma around, for example, introducing online voting is simply "don't", but if we want to expand the role of voting-like mechanisms, including more advanced forms such as quadratic voting and quadratic finance, to more roles, we have no choice but to confront the challenge head-on, try really hard, and hopefully succeed at making something secure enough, for at least some use cases. -
![[Mirror] Cantor was Wrong: debunking the infinite set hierarchy](https://fastly.jsdelivr.net/npm/typecho-joe-next@6.0.0/assets/img/lazyload.jpg) [Mirror] Cantor was Wrong: debunking the infinite set hierarchy [Mirror] Cantor was Wrong: debunking the infinite set hierarchy2019 Apr 01 See all posts [Mirror] Cantor was Wrong: debunking the infinite set hierarchy This is a mirror of the post at https://medium.com/@VitalikButerin/cantor-was-wrong-debunking-the-infinite-set-hierarchy-e9ba5015102.By Vitalik Buterin, PhD at University of BaselA common strand of mathematics argues that, rather than being one single kind of infinity, there are actually an infinite hierarchy of different levels of infinity. Whereas the size of the set of integers is just plain infinite, and the set of rational numbers is just as big as the integers (because you can map every rational number to an integer by interleaving the digits of its numerator and denominator, eg. \(0.456456456.... = \frac = \frac \rightarrow 135323\)), the size of the set of real numbers is some kind of even bigger infinity, because there is no way to make a similar mapping from real numbers to the integers.First of all, I should note that it's relatively easy to see that the claim that there is no mapping is false. Here's a simple mapping. For a given real number, give me a (deterministic) python program that will print out digits of it (eg. for π, that might be a program that calculates better and better approximations using the infinite series \(\pi = 4 - \frac + \frac - \frac + ...\)). I can convert the program into a number (using n = int.from_bytes(open('program.py').read(), 'big')) and then output the number. Done. There's the mapping from real numbers to integers.Now let's take a look at the most common argument used to claim that no such mapping can exist, namely Cantor's diagonal argument. Here's an exposition from UC Denver; it's short so I'll just screenshot the whole thing:Now, here's the fundamental flaw in this argument: decimal expansions of real numbers are not unique. To provide a counterexample in the exact format that the "proof" requires, consider the set (numbers written in binary), with diagonal digits bolded:x[1] = 0.000000... x[2] = 0.011111... x[3] = 0.001111... x[4] = 0.000111... ..... The diagonal gives: 01111..... If we flip every digit, we get the number: \(y =\) 0.10000......And here lies the problem: just as in decimal, 0.9999.... equals 1, in binary 0.01111..... equals 0.10000..... And so even though the new decimal expansion is not in the original list, the number \(y\) is exactly the same as the number \(x[2]\).Note that this directly implies that the halting problem is in fact solvable. To see why, imagine a computer program that someone claims will not halt. Let c[1] be the state of the program after one step, c[2] after two steps, etc. Let x[1], x[2], x[3].... be a full enumeration of all real numbers (which exists, as we proved above), expressed in base \(2^D\) where \(D\) is the size of the program's memory, so a program state can always be represented as a single "digit". Let y = 0.c[1]c[2]c[3]........ This number is by assumption part of the list, so it is one of the x[i] values, and hence it can be computed in some finite amount of time. This has implications in a number of industries, particularly in proving that "Turing-complete" blockchains are in fact secure.Patent on this research is pending.
[Mirror] Cantor was Wrong: debunking the infinite set hierarchy [Mirror] Cantor was Wrong: debunking the infinite set hierarchy2019 Apr 01 See all posts [Mirror] Cantor was Wrong: debunking the infinite set hierarchy This is a mirror of the post at https://medium.com/@VitalikButerin/cantor-was-wrong-debunking-the-infinite-set-hierarchy-e9ba5015102.By Vitalik Buterin, PhD at University of BaselA common strand of mathematics argues that, rather than being one single kind of infinity, there are actually an infinite hierarchy of different levels of infinity. Whereas the size of the set of integers is just plain infinite, and the set of rational numbers is just as big as the integers (because you can map every rational number to an integer by interleaving the digits of its numerator and denominator, eg. \(0.456456456.... = \frac = \frac \rightarrow 135323\)), the size of the set of real numbers is some kind of even bigger infinity, because there is no way to make a similar mapping from real numbers to the integers.First of all, I should note that it's relatively easy to see that the claim that there is no mapping is false. Here's a simple mapping. For a given real number, give me a (deterministic) python program that will print out digits of it (eg. for π, that might be a program that calculates better and better approximations using the infinite series \(\pi = 4 - \frac + \frac - \frac + ...\)). I can convert the program into a number (using n = int.from_bytes(open('program.py').read(), 'big')) and then output the number. Done. There's the mapping from real numbers to integers.Now let's take a look at the most common argument used to claim that no such mapping can exist, namely Cantor's diagonal argument. Here's an exposition from UC Denver; it's short so I'll just screenshot the whole thing:Now, here's the fundamental flaw in this argument: decimal expansions of real numbers are not unique. To provide a counterexample in the exact format that the "proof" requires, consider the set (numbers written in binary), with diagonal digits bolded:x[1] = 0.000000... x[2] = 0.011111... x[3] = 0.001111... x[4] = 0.000111... ..... The diagonal gives: 01111..... If we flip every digit, we get the number: \(y =\) 0.10000......And here lies the problem: just as in decimal, 0.9999.... equals 1, in binary 0.01111..... equals 0.10000..... And so even though the new decimal expansion is not in the original list, the number \(y\) is exactly the same as the number \(x[2]\).Note that this directly implies that the halting problem is in fact solvable. To see why, imagine a computer program that someone claims will not halt. Let c[1] be the state of the program after one step, c[2] after two steps, etc. Let x[1], x[2], x[3].... be a full enumeration of all real numbers (which exists, as we proved above), expressed in base \(2^D\) where \(D\) is the size of the program's memory, so a program state can always be represented as a single "digit". Let y = 0.c[1]c[2]c[3]........ This number is by assumption part of the list, so it is one of the x[i] values, and hence it can be computed in some finite amount of time. This has implications in a number of industries, particularly in proving that "Turing-complete" blockchains are in fact secure.Patent on this research is pending. -
 A CBC Casper Tutorial A CBC Casper Tutorial2018 Dec 05 See all posts A CBC Casper Tutorial Special thanks to Vlad Zamfir, Aditya Asgaonkar, Ameen Soleimani and Jinglan Wang for reviewIn order to help more people understand "the other Casper" (Vlad Zamfir's CBC Casper), and specifically the instantiation that works best for blockchain protocols, I thought that I would write an explainer on it myself, from a less abstract and more "close to concrete usage" point of view. Vlad's descriptions of CBC Casper can be found here and here and here; you are welcome and encouraged to look through these materials as well.CBC Casper is designed to be fundamentally very versatile and abstract, and come to consensus on pretty much any data structure; you can use CBC to decide whether to choose 0 or 1, you can make a simple block-by-block chain run on top of CBC, or a \(2^\)-dimensional hypercube tangle DAG, and pretty much anything in between.But for simplicity, we will first focus our attention on one concrete case: a simple chain-based structure. We will suppose that there is a fixed validator set consisting of \(N\) validators (a fancy word for "staking nodes"; we also assume that each node is staking the same amount of coins, cases where this is not true can be simulated by assigning some nodes multiple validator IDs), time is broken up into ten-second slots, and validator \(k\) can create a block in slot \(k\), \(N + k\), \(2N + k\), etc. Each block points to one specific parent block. Clearly, if we wanted to make something maximally simple, we could just take this structure, impose a longest chain rule on top of it, and call it a day. The green chain is the longest chain (length 6) so it is considered to be the "canonical chain".However, what we care about here is adding some notion of "finality" - the idea that some block can be so firmly established in the chain that it cannot be overtaken by a competing block unless a very large portion (eg. \(\frac\)) of validators commit a uniquely attributable fault - act in some way which is clearly and cryptographically verifiably malicious. If a very large portion of validators do act maliciously to revert the block, proof of the misbehavior can be submitted to the chain to take away those validators' entire deposits, making the reversion of finality extremely expensive (think hundreds of millions of dollars).LMD GHOSTWe will take this one step at a time. First, we replace the fork choice rule (the rule that chooses which chain among many possible choices is "the canonical chain", ie. the chain that users should care about), moving away from the simple longest-chain-rule and instead using "latest message driven GHOST". To show how LMD GHOST works, we will modify the above example. To make it more concrete, suppose the validator set has size 5, which we label \(A\), \(B\), \(C\), \(D\), \(E\), so validator \(A\) makes the blocks at slots 0 and 5, validator \(B\) at slots 1 and 6, etc. A client evaluating the LMD GHOST fork choice rule cares only about the most recent (ie. highest-slot) message (ie. block) signed by each validator: Latest messages in blue, slots from left to right (eg. \(A\)'s block on the left is at slot 0, etc.)Now, we will use only these messages as source data for the "greedy heaviest observed subtree" (GHOST) fork choice rule: start at the genesis block, then each time there is a fork choose the side where more of the latest messages support that block's subtree (ie. more of the latest messages support either that block or one of its descendants), and keep doing this until you reach a block with no children. We can compute for each block the subset of latest messages that support either the block or one of its descendants: Now, to compute the head, we start at the beginning, and then at each fork pick the higher number: first, pick the bottom chain as it has 4 latest messages supporting it versus 1 for the single-block top chain, then at the next fork support the middle chain. The result is the same longest chain as before. Indeed, in a well-running network (ie. the orphan rate is low), almost all of the time LMD GHOST and the longest chain rule will give the exact same answer. But in more extreme circumstances, this is not always true. For example, consider the following chain, with a more substantial three-block fork: Scoring blocks by chain length. If we follow the longest chain rule, the top chain is longer, so the top chain wins. Scoring blocks by number of supporting latest messages and using the GHOST rule (latest message from each validator shown in blue). The bottom chain has more recent support, so if we follow the LMD GHOST rule the bottom chain wins, though it's not yet clear which of the three blocks takes precedence.The LMD GHOST approach is advantageous in part because it is better at extracting information in conditions of high latency. If two validators create two blocks with the same parent, they should really be both counted as cooperating votes for the parent block, even though they are at the same time competing votes for themselves. The longest chain rule fails to capture this nuance; GHOST-based rules do.Detecting finalityBut the LMD GHOST approach has another nice property: it's sticky. For example, suppose that for two rounds, \(\frac\) of validators voted for the same chain (we'll assume that the one of the five validators that did not, \(B\), is attacking): What would need to actually happen for the chain on top to become the canonical chain? Four of five validators built on top of \(E\)'s first block, and all four recognized that \(E\) had a high score in the LMD fork choice. Just by looking at the structure of the chain, we can know for a fact at least some of the messages that the validators must have seen at different times. Here is what we know about the four validators' views: A's view C's view D's view E's view Blocks produced by each validator in green, the latest messages we know that they saw from each of the other validators in blue. Note that all four of the validators could have seen one or both of \(B\)'s blocks, and \(D\) and \(E\) could have seen \(C\)'s second block, making that the latest message in their views instead of \(C\)'s first block; however, the structure of the chain itself gives us no evidence that they actually did. Fortunately, as we will see below, this ambiguity does not matter for us.\(A\)'s view contains four latest-messages supporting the bottom chain, and none supporting \(B\)'s block. Hence, in (our simulation of) \(A\)'s eyes the score in favor of the bottom chain is at least 4-1. The views of \(C\), \(D\) and \(E\) paint a similar picture, with four latest-messages supporting the bottom chain. Hence, all four of the validators are in a position where they cannot change their minds unless two other validators change their minds first to bring the score to 2-3 in favor of \(B\)'s block.Note that our simulation of the validators' views is "out of date" in that, for example, it does not capture that \(D\) and \(E\) could have seen the more recent block by \(C\). However, this does not alter the calculation for the top vs bottom chain, because we can very generally say that any validator's new message will have the same opinion as their previous messages, unless two other validators have already switched sides first. A minimal viable attack. \(A\) and \(C\) illegally switch over to support \(B\)'s block (and can get penalized for this), giving it a 3-2 advantage, and at this point it becomes legal for \(D\) and \(E\) to also switch over. Since fork choice rules such as LMD GHOST are sticky in this way, and clients can detect when the fork choice rule is "stuck on" a particular block, we can use this as a way of achieving asynchronously safe consensus.Safety OraclesActually detecting all possible situations where the chain becomes stuck on some block (in CBC lingo, the block is "decided" or "safe") is very difficult, but we can come up with a set of heuristics ("safety oracles") which will help us detect some of the cases where this happens. The simplest of these is the clique oracle. If there exists some subset \(V\) of the validators making up portion \(p\) of the total validator set (with \(p > \frac\)) that all make blocks supporting some block \(B\) and then make another round of blocks still supporting \(B\) that references their first round of blocks, then we can reason as follows:Because of the two rounds of messaging, we know that this subset \(V\) all (i) support \(B\) (ii) know that \(B\) is well-supported, and so none of them can legally switch over unless enough others switch over first. For some competing \(B'\) to beat out \(B\), the support such a \(B'\) can legally have is initially at most \(1-p\) (everyone not part of the clique), and to win the LMD GHOST fork choice its support needs to get to \(\frac\), so at least \(\frac - (1-p) = p - \frac\) need to illegally switch over to get it to the point where the LMD GHOST rule supports \(B'\).As a specific case, note that the \(p=\frac\) clique oracle offers a \(\frac\) level of safety, and a set of blocks satisfying the clique can (and in normal operation, will) be generated as long as \(\frac\) of nodes are online. Hence, in a BFT sense, the level of fault tolerance that can be reached using two-round clique oracles is \(\frac\), in terms of both liveness and safety.This approach to consensus has many nice benefits. First of all, the short-term chain selection algorithm, and the "finality algorithm", are not two awkwardly glued together distinct components, as they admittedly are in Casper FFG; rather, they are both part of the same coherent whole. Second, because safety detection is client-side, there is no need to choose any thresholds in-protocol; clients can decide for themselves what level of safety is sufficient to consider a block as finalized.Going FurtherCBC can be extended further in many ways. First, one can come up with other safety oracles; higher-round clique oracles can reach \(\frac\) fault tolerance. Second, we can add validator rotation mechanisms. The simplest is to allow the validator set to change by a small percentage every time the \(q=\frac\) clique oracle is satisfied, but there are other things that we can do as well. Third, we can go beyond chain-like structures, and instead look at structures that increase the density of messages per unit time, like the Serenity beacon chain's attestation structure: In this case, it becomes worthwhile to separate attestations from blocks; a block is an object that actually grows the underlying DAG, whereas an attestation contributes to the fork choice rule. In the Serenity beacon chain spec, each block may have hundreds of attestations corresponding to it. However, regardless of which way you do it, the core logic of CBC Casper remains the same.To make CBC Casper's safety "cryptoeconomically enforceable", we need to add validity and slashing conditions. First, we'll start with the validity rule. A block contains both a parent block and a set of attestations that it knows about that are not yet part of the chain (similar to "uncles" in the current Ethereum PoW chain). For the block to be valid, the block's parent must be the result of executing the LMD GHOST fork choice rule given the information included in the chain including in the block itself. Dotted lines are uncle links, eg. when E creates a block, E notices that C is not yet part of the chain, and so includes a reference to C.We now can make CBC Casper safe with only one slashing condition: you cannot make two attestations \(M_1\) and \(M_2\), unless either \(M_1\) is in the chain that \(M_2\) is attesting to or \(M_2\) is in the chain that \(M_2\) is attesting to. OK Not OK The validity and slashing conditions are relatively easy to describe, though actually implementing them requires checking hash chains and executing fork choice rules in-consensus, so it is not nearly as simple as taking two messages and checking a couple of inequalities between the numbers that these messages commit to, as you can do in Casper FFG for the NO_SURROUND and NO_DBL_VOTE slashing conditions.Liveness in CBC Casper piggybacks off of the liveness of whatever the underlying chain algorithm is (eg. if it's one-block-per-slot, then it depends on a synchrony assumption that all nodes will see everything produced in slot \(N\) before the start of slot \(N+1\)). It's not possible to get "stuck" in such a way that one cannot make progress; it's possible to get to the point of finalizing new blocks from any situation, even one where there are attackers and/or network latency is higher than that required by the underlying chain algorithm.Suppose that at some time \(T\), the network "calms down" and synchrony assumptions are once again satisfied. Then, everyone will converge on the same view of the chain, with the same head \(H\). From there, validators will begin to sign messages supporting \(H\) or descendants of \(H\). From there, the chain can proceed smoothly, and will eventually satisfy a clique oracle, at which point \(H\) becomes finalized. Chaotic network due to high latency. Network latency subsides, a majority of validators see all of the same blocks or at least enough of them to get to the same head when executing the fork choice, and start building on the head, further reinforcing its advantage in the fork choice rule. Chain proceeds "peacefully" at low latency. Soon, a clique oracle will be satisfied.That's all there is to it! Implementation-wise, CBC may arguably be considerably more complex than FFG, but in terms of ability to reason about the protocol, and the properties that it provides, it's surprisingly simple.
A CBC Casper Tutorial A CBC Casper Tutorial2018 Dec 05 See all posts A CBC Casper Tutorial Special thanks to Vlad Zamfir, Aditya Asgaonkar, Ameen Soleimani and Jinglan Wang for reviewIn order to help more people understand "the other Casper" (Vlad Zamfir's CBC Casper), and specifically the instantiation that works best for blockchain protocols, I thought that I would write an explainer on it myself, from a less abstract and more "close to concrete usage" point of view. Vlad's descriptions of CBC Casper can be found here and here and here; you are welcome and encouraged to look through these materials as well.CBC Casper is designed to be fundamentally very versatile and abstract, and come to consensus on pretty much any data structure; you can use CBC to decide whether to choose 0 or 1, you can make a simple block-by-block chain run on top of CBC, or a \(2^\)-dimensional hypercube tangle DAG, and pretty much anything in between.But for simplicity, we will first focus our attention on one concrete case: a simple chain-based structure. We will suppose that there is a fixed validator set consisting of \(N\) validators (a fancy word for "staking nodes"; we also assume that each node is staking the same amount of coins, cases where this is not true can be simulated by assigning some nodes multiple validator IDs), time is broken up into ten-second slots, and validator \(k\) can create a block in slot \(k\), \(N + k\), \(2N + k\), etc. Each block points to one specific parent block. Clearly, if we wanted to make something maximally simple, we could just take this structure, impose a longest chain rule on top of it, and call it a day. The green chain is the longest chain (length 6) so it is considered to be the "canonical chain".However, what we care about here is adding some notion of "finality" - the idea that some block can be so firmly established in the chain that it cannot be overtaken by a competing block unless a very large portion (eg. \(\frac\)) of validators commit a uniquely attributable fault - act in some way which is clearly and cryptographically verifiably malicious. If a very large portion of validators do act maliciously to revert the block, proof of the misbehavior can be submitted to the chain to take away those validators' entire deposits, making the reversion of finality extremely expensive (think hundreds of millions of dollars).LMD GHOSTWe will take this one step at a time. First, we replace the fork choice rule (the rule that chooses which chain among many possible choices is "the canonical chain", ie. the chain that users should care about), moving away from the simple longest-chain-rule and instead using "latest message driven GHOST". To show how LMD GHOST works, we will modify the above example. To make it more concrete, suppose the validator set has size 5, which we label \(A\), \(B\), \(C\), \(D\), \(E\), so validator \(A\) makes the blocks at slots 0 and 5, validator \(B\) at slots 1 and 6, etc. A client evaluating the LMD GHOST fork choice rule cares only about the most recent (ie. highest-slot) message (ie. block) signed by each validator: Latest messages in blue, slots from left to right (eg. \(A\)'s block on the left is at slot 0, etc.)Now, we will use only these messages as source data for the "greedy heaviest observed subtree" (GHOST) fork choice rule: start at the genesis block, then each time there is a fork choose the side where more of the latest messages support that block's subtree (ie. more of the latest messages support either that block or one of its descendants), and keep doing this until you reach a block with no children. We can compute for each block the subset of latest messages that support either the block or one of its descendants: Now, to compute the head, we start at the beginning, and then at each fork pick the higher number: first, pick the bottom chain as it has 4 latest messages supporting it versus 1 for the single-block top chain, then at the next fork support the middle chain. The result is the same longest chain as before. Indeed, in a well-running network (ie. the orphan rate is low), almost all of the time LMD GHOST and the longest chain rule will give the exact same answer. But in more extreme circumstances, this is not always true. For example, consider the following chain, with a more substantial three-block fork: Scoring blocks by chain length. If we follow the longest chain rule, the top chain is longer, so the top chain wins. Scoring blocks by number of supporting latest messages and using the GHOST rule (latest message from each validator shown in blue). The bottom chain has more recent support, so if we follow the LMD GHOST rule the bottom chain wins, though it's not yet clear which of the three blocks takes precedence.The LMD GHOST approach is advantageous in part because it is better at extracting information in conditions of high latency. If two validators create two blocks with the same parent, they should really be both counted as cooperating votes for the parent block, even though they are at the same time competing votes for themselves. The longest chain rule fails to capture this nuance; GHOST-based rules do.Detecting finalityBut the LMD GHOST approach has another nice property: it's sticky. For example, suppose that for two rounds, \(\frac\) of validators voted for the same chain (we'll assume that the one of the five validators that did not, \(B\), is attacking): What would need to actually happen for the chain on top to become the canonical chain? Four of five validators built on top of \(E\)'s first block, and all four recognized that \(E\) had a high score in the LMD fork choice. Just by looking at the structure of the chain, we can know for a fact at least some of the messages that the validators must have seen at different times. Here is what we know about the four validators' views: A's view C's view D's view E's view Blocks produced by each validator in green, the latest messages we know that they saw from each of the other validators in blue. Note that all four of the validators could have seen one or both of \(B\)'s blocks, and \(D\) and \(E\) could have seen \(C\)'s second block, making that the latest message in their views instead of \(C\)'s first block; however, the structure of the chain itself gives us no evidence that they actually did. Fortunately, as we will see below, this ambiguity does not matter for us.\(A\)'s view contains four latest-messages supporting the bottom chain, and none supporting \(B\)'s block. Hence, in (our simulation of) \(A\)'s eyes the score in favor of the bottom chain is at least 4-1. The views of \(C\), \(D\) and \(E\) paint a similar picture, with four latest-messages supporting the bottom chain. Hence, all four of the validators are in a position where they cannot change their minds unless two other validators change their minds first to bring the score to 2-3 in favor of \(B\)'s block.Note that our simulation of the validators' views is "out of date" in that, for example, it does not capture that \(D\) and \(E\) could have seen the more recent block by \(C\). However, this does not alter the calculation for the top vs bottom chain, because we can very generally say that any validator's new message will have the same opinion as their previous messages, unless two other validators have already switched sides first. A minimal viable attack. \(A\) and \(C\) illegally switch over to support \(B\)'s block (and can get penalized for this), giving it a 3-2 advantage, and at this point it becomes legal for \(D\) and \(E\) to also switch over. Since fork choice rules such as LMD GHOST are sticky in this way, and clients can detect when the fork choice rule is "stuck on" a particular block, we can use this as a way of achieving asynchronously safe consensus.Safety OraclesActually detecting all possible situations where the chain becomes stuck on some block (in CBC lingo, the block is "decided" or "safe") is very difficult, but we can come up with a set of heuristics ("safety oracles") which will help us detect some of the cases where this happens. The simplest of these is the clique oracle. If there exists some subset \(V\) of the validators making up portion \(p\) of the total validator set (with \(p > \frac\)) that all make blocks supporting some block \(B\) and then make another round of blocks still supporting \(B\) that references their first round of blocks, then we can reason as follows:Because of the two rounds of messaging, we know that this subset \(V\) all (i) support \(B\) (ii) know that \(B\) is well-supported, and so none of them can legally switch over unless enough others switch over first. For some competing \(B'\) to beat out \(B\), the support such a \(B'\) can legally have is initially at most \(1-p\) (everyone not part of the clique), and to win the LMD GHOST fork choice its support needs to get to \(\frac\), so at least \(\frac - (1-p) = p - \frac\) need to illegally switch over to get it to the point where the LMD GHOST rule supports \(B'\).As a specific case, note that the \(p=\frac\) clique oracle offers a \(\frac\) level of safety, and a set of blocks satisfying the clique can (and in normal operation, will) be generated as long as \(\frac\) of nodes are online. Hence, in a BFT sense, the level of fault tolerance that can be reached using two-round clique oracles is \(\frac\), in terms of both liveness and safety.This approach to consensus has many nice benefits. First of all, the short-term chain selection algorithm, and the "finality algorithm", are not two awkwardly glued together distinct components, as they admittedly are in Casper FFG; rather, they are both part of the same coherent whole. Second, because safety detection is client-side, there is no need to choose any thresholds in-protocol; clients can decide for themselves what level of safety is sufficient to consider a block as finalized.Going FurtherCBC can be extended further in many ways. First, one can come up with other safety oracles; higher-round clique oracles can reach \(\frac\) fault tolerance. Second, we can add validator rotation mechanisms. The simplest is to allow the validator set to change by a small percentage every time the \(q=\frac\) clique oracle is satisfied, but there are other things that we can do as well. Third, we can go beyond chain-like structures, and instead look at structures that increase the density of messages per unit time, like the Serenity beacon chain's attestation structure: In this case, it becomes worthwhile to separate attestations from blocks; a block is an object that actually grows the underlying DAG, whereas an attestation contributes to the fork choice rule. In the Serenity beacon chain spec, each block may have hundreds of attestations corresponding to it. However, regardless of which way you do it, the core logic of CBC Casper remains the same.To make CBC Casper's safety "cryptoeconomically enforceable", we need to add validity and slashing conditions. First, we'll start with the validity rule. A block contains both a parent block and a set of attestations that it knows about that are not yet part of the chain (similar to "uncles" in the current Ethereum PoW chain). For the block to be valid, the block's parent must be the result of executing the LMD GHOST fork choice rule given the information included in the chain including in the block itself. Dotted lines are uncle links, eg. when E creates a block, E notices that C is not yet part of the chain, and so includes a reference to C.We now can make CBC Casper safe with only one slashing condition: you cannot make two attestations \(M_1\) and \(M_2\), unless either \(M_1\) is in the chain that \(M_2\) is attesting to or \(M_2\) is in the chain that \(M_2\) is attesting to. OK Not OK The validity and slashing conditions are relatively easy to describe, though actually implementing them requires checking hash chains and executing fork choice rules in-consensus, so it is not nearly as simple as taking two messages and checking a couple of inequalities between the numbers that these messages commit to, as you can do in Casper FFG for the NO_SURROUND and NO_DBL_VOTE slashing conditions.Liveness in CBC Casper piggybacks off of the liveness of whatever the underlying chain algorithm is (eg. if it's one-block-per-slot, then it depends on a synchrony assumption that all nodes will see everything produced in slot \(N\) before the start of slot \(N+1\)). It's not possible to get "stuck" in such a way that one cannot make progress; it's possible to get to the point of finalizing new blocks from any situation, even one where there are attackers and/or network latency is higher than that required by the underlying chain algorithm.Suppose that at some time \(T\), the network "calms down" and synchrony assumptions are once again satisfied. Then, everyone will converge on the same view of the chain, with the same head \(H\). From there, validators will begin to sign messages supporting \(H\) or descendants of \(H\). From there, the chain can proceed smoothly, and will eventually satisfy a clique oracle, at which point \(H\) becomes finalized. Chaotic network due to high latency. Network latency subsides, a majority of validators see all of the same blocks or at least enough of them to get to the same head when executing the fork choice, and start building on the head, further reinforcing its advantage in the fork choice rule. Chain proceeds "peacefully" at low latency. Soon, a clique oracle will be satisfied.That's all there is to it! Implementation-wise, CBC may arguably be considerably more complex than FFG, but in terms of ability to reason about the protocol, and the properties that it provides, it's surprisingly simple. -
![[Mirror] Central Planning as Overfitting](https://fastly.jsdelivr.net/npm/typecho-joe-next@6.0.0/assets/img/lazyload.jpg) [Mirror] Central Planning as Overfitting [Mirror] Central Planning as Overfitting2018 Nov 25 See all posts [Mirror] Central Planning as Overfitting This is a mirror of the post at https://radicalxchange.org/blog/posts/2018-11-26-4m9b8b/ written by myself and Glen WeylThere is an intuition shared by many that "central planning" — command-and-control techniques for allocating resources in economies, and fine-grained knob-turning interventionism more generally — is undesirable. There's quite a lot to this, but it is often misapplied in a way that also leads it to go under-appreciated. In this post we try to clarify the appropriate scope of the intuition.Some recent examples of the intuition being misapplied are:People arguing that relatively simple entitlement programs like Social Security are burdensome government intervention, while elaborate and often discretionary tax breaks conditional on specific behaviors are a good step towards less government. People arguing that block size limits in cryptocurrencies, which impose a hard cap on the number of transactions that each block can contain, are a form of central planning, but who do not argue against other centrally planned parameters, eg. the targeted ten minute (or whatever) average time interval between blocks. People arguing that a lack of block size limits constitutes central planning (!!) People arguing that fixed transaction fees constitute central planning, but variable transaction fees that arise out of an equilibrium itself created by a fixed block size limit do not. We were recently at a discussion in policy circles in Washington, where one of us was arguing for a scheme based on Harberger taxes for spectrum licenses, debating against someone defending more conventional perpetual monopoly licenses on spectrum aggregated at large levels that would tend to create a few national cellular carriers. The latter side argued that the Harberger tax scheme constituted unacceptable bureaucratic interventionism, but seemed to believe that permanent government-issued monopoly privileges are a property right as natural as apples falling from a tree. While we do not entirely dismiss this last example, for reasons we will return to later, it does seem overplayed. Similarly and conversely, we see many examples where, in the name of defending or promoting "markets" (or at least "economic rationality") many professional economists advocate schemes that seem much more to us like central planning than the systems they seek to replace:The most systematic example of this is the literature on "optimal mechanism design," which began with the already extremely complicated and fragile Vickrey-Clarke-Groves mechanism and has only gotten more byzantine from there. While Vickrey's motivation for these ideas was to discover relatively simple rules that would correct the flaws of standard capitalism, he acknowledged in his paper that the design was highly complex in its direct application and urged future researchers to find simplifications. Instead of following this counsel, many scholars have proposed, for example, schemes that rely on a central authority being able to specify an infinite dimensional set of prior beliefs. These schemes, we submit, constitute "central planning" in precisely the sense we should be concerned with. Furthermore, these designs are not just matters of theory, but in practice many applied mechanism designers have created systems with similar properties. The recent United States Spectrum Incentive auctions (designed by a few prominent economists and computer scientists) centralized the enforcement of potential conflicts between transmission rights using an extremely elaborate and opaque computational engine, rather than allowing conflicts to be resolved through (for example) common law liability lawsuits as other interference between property claims and land uses are. A recent design for the allocation of courses to students at the University of Pennsylvania designed by a similar team requires students to express their preferences over courses on a novel numerical scale, allowing them only narrow language for expressing complementarities and substitutability between courses and then uses a state-of-the-art optimization engine to allocate courses. Auction systems designed by economists and computer scientists at large technology companies, like Facebook and Google, are even richer and less transparent, and have created substantial backlash, inspiring a whole industry of firms that help advertisers optimize their bidding in elaborate ways against these systems. This problem does not merely arise in mechanism design, however. In the fields of industrial organization (the basis of much antitrust economics) and the field of macroeconomics (the basis of much monetary policy), extremely elaborate models with hundreds of parameters are empirically estimated and used to simulate the effects of mergers or changes in monetary policy. These models are usually difficult to explain even to experts in the field, much less democratically-elected politicians, judges or, god forbid, voters. And yet the confidence we have in these models, the empirical evidence validating their accuracy, etc. is almost nothing. Nonetheless, economists consistently promote such methods as "the state of the art" and they are generally viewed positively by defenders of the "market economy". To understand why we think the concept of "intervention" is being misapplied here, we need to understand two different ways of measuring the extent to which some scheme is "interventionist". The first approach is to try to measure the absolute magnitude of distortion relative to some imagined state of nature (anarcho-primitivism, or a blockchain with no block size limits, or...). However, this approach clearly fails to capture the intuitions of why central planning is undesirable. For example, property rights in the physical world are a large intervention into almost every person's behavior, considerably limiting the actions that we can take every day. Many of these restrictions are actually of quite recent historical provenance (beginning with agriculture, and mostly in the West and not the East or Middle East). However, opponents of central planning often tend to be the strongest proponents of property rights!We can shed some light on this puzzle by looking at another way of measuring the "central-planny-ness" of some social structure: in short, measure the number of knobs. Property rights actually score quite well here: every piece of property is allocated to some person or legal entity, they can use it as they wish, and no one else can touch it without their permission. There are choices to make around the edges (eg. adverse possession rights), but generally there isn't too much room for changing the scheme around (though note that privatization schemes, ie. transitions from something other than property rights to property rights like the auctions we discussed above, have very many knobs, and so there we can see more risks). Command-and-control regulations with ten thousand clauses (or market designs that specify elaborate probabilistic objects, or optimization protocols, etc.), or attempts to limit use of specific features of the blockchain to drive out specific categories of users, are much less desirable, as such strategies leave many more choices to central planners. A block size limit and a fixed transaction fee (or carbon taxes and a cap-and-trade scheme) have the exact same level of "central-planny-ness" to them: one variable (either quantity or price) is fixed in the protocol, and the other variable is left to the market.Here are some key underlying reasons why we believe that simple social systems with fewer knobs are so desirable:They have fewer moving parts that can fail or otherwise have unexpected effects. They are less likely to overfit. If a social system is too complex, there are many parameters to set and relatively few experiences to draw from when setting the parameters, making it more likely that the parameters will be set to overfit to one context, and generalize poorly to other places or to future times. We know little, and we should not design systems that demand us to know a lot. They are more resistant to corruption. If a social system is simpler, it is more difficult (not impossible, but still more difficult) to set parameters in ways that encode attempts to privilege or anti-privilege specific individuals, factions or communities. This is not only good because it leads to fairness, it is also good because it leads to less zero-sum conflict. They can more easily achieve legitimacy. Because simpler systems are easier to understand, and easier for people to understand that a given implementation is not unfairly privileging special interests, it is easier to create common knowledge that the system is fair, creating a stronger sense of trust. Legitimacy is perhaps the central virtue of social institutions, as it sustains cooperation and coordination, enables the possibility of democracy (how can you democratically participate and endorse a system you do not understand?) and allows for a bottoms-up, rather than top-down, creation of a such a system, ensuring it can be implemented without much coercion or violence. These effects are not always achieved (for example, even if a system has very few knobs, it's often the case that there exists a knob that can be turned to privilege well-connected and wealthy people as a class over everyone else), but the simpler a system is, the more likely the effects are to be achieved.While avoiding over-complexity and overfit in personal decision-making is also important, avoiding these issues in large-scale social systems is even more important, because of the inevitable possibility of powerful forces attempting to manipulate knobs for the benefit of special interests, and the need to achieve common knowledge that the system has not been greatly corrupted, to the point where the fairness of the system is obvious even to unsophisticated observers.This is not to condemn all forms or uses of complexity in social systems. Most science and the inner workings of many technical systems are likely to be opaque to the public but this does not mean science or technology is useless in social life; far from it. However, these systems, to gain legitimacy, usually show that they can reliably achieve some goal, which is transparent and verifiable. Planes land safely and on time, computational systems seem to deliver calculations that are correct, etc. It is by this process of verification, rather than by the transparency of the system per se, that such systems gain their legitimacy. However, for many social systems, truly large-scale, repeatable tests are difficult if not impossible. As such, simplicity is usually critical to legitimacy.Different Notions of SimplicityHowever, there is one class of social systems that seem to be desirable, and that intellectual advocates of minimizing central planning tend to agree are desirable, that don't quite fit the simple "few knobs" characterization that we made above. For example, consider common law. Common law is built up over thousands of precedents, and contains a large number of concepts (eg. see this list under "property law", itself only a part of common law; have you heard of "quicquid plantatur solo, solo cedit" before?). However, proponents of private property are very frequently proponents of common law. So what gives?Here, we need to make a distinction between redundant complexity, or many knobs that really all serve a relatively small number of similar goals, and optimizing complexity, in the extreme one knob per problem that the system has encountered. In computational complexity theory, we typically talk about Kolmogorov complexity, but there are other notions of complexity that are also useful here, particularly VC dimension - roughly, the size of the largest set of situations for which we can turn the knobs in a particular way to achieve any particular set of outcomes. Many successful machine learning techniques, such as Support Vector Machines and Boosting, are quite complex, both in the formal Kolmogorov sense and in terms of the outcomes they produce, but can be proven to have low VC dimension.VC dimension does a nice job capturing some of the arguments for simplicity mentioned above more explicitly, for example:A system with low VC dimension may have some moving parts that fail, but if it does, its different constituent parts can correct for each other. By construction, it has built in resilience through redundancy Low VC dimension is literally a measure of resistance to overfit. Low VC dimension leads to resistance to corruption, because if VC dimension is low, a corrupt or self-interested party in control of some knobs will not as easily be able to achieve some particular outcome that they desire. In particular, this agent will be "checked and balanced" by other parts of the system that redundantly achieve the originally desired ends. They can achieve legitimacy because people can randomly check a few parts and verify in detail that those parts work in ways that are reasonable, and assume that the rest of the system works in a similar way. An example of this was the ratification of the United States Constitution which, while quite elaborate, was primarily elaborate in the redundancy with which it applied the principle of checks and balances of power. Thus most citizens only read one or a few of The Federalist Papers that explained and defended the Constitution, and yet got a reasonable sense for what was going on. This is not as clean and convenient as a system with low Kolmogorov complexity, but still much better than a system with high complexity where the complexity is "optimizing" (for an example of this in the blockchain context, see Vitalik's opposition and alternative to on-chain governance). The primary disadvantage we see in Kolmogorov complex but VC simple designs is for new social institutions, where it may be hard to persuade the public that these are VC simple. VC simplicity is usually easier as a basis for legitimacy when an institutions has clearly been built up without any clear design over a long period of time or by a large committee of people with conflicting interests (as with the United States Constitution). Thus when offering innovations we tend to focus more on Kolmogorov simplicity and hope many redundant each Kolmogorov-simple elements will add up to a VC-simple system. However, we may just not have the imagination to think of how VC simplicity might be effectively explained.There are forms of the "avoid central planning" intuition that are misunderstandings and ultimately counterproductive. For example, try to automatically seize upon designs that seem at first glance to "look like a market", because not all markets are created equal. For example, one of us has argued for using fixed prices in certain settings to reduce uncertainty, and the other has (for similar information sharing reasons) argued for auctions that are a synthesis of standard descending price Dutch and ascending price English auctions (Channel auctions). That said, it is also equally a large error to throw the intuition away entirely. Rather, it is a valuable and important insight that can easily is central to the methodology we have been recently trying to develop. Simplicity to Whom? Or Why Humanities MatterHowever, the academic critics of this type of work are not simply confused. There is a reasonable basis for unease with discussions of "simplicity" because they inevitably contain a degree of subjectivity. What is "simple" to describe or appears to have few knobs in one language for describing it is devilishly complex in another, and vice versa. A few examples should help illuminate the point:We have repeatedly referred to "knobs", which are roughly real valued parameters. But real-valued parameters can encode an arbitrary amount of complexity. For example, I could claim my system has only one knob, it is just that slight changes in the 1000th decimal place of the setting of that knob end up determining incredibly important properties of the system. This may seem cheap, but more broadly it is the case that non-linear mappings between systems can make one system seem "simple" and another "complex" and in general there is just no way to say which is right. Many think of the electoral system of the United States as "simple", and yet, if one reflects on it or tries to explain it to a foreigner, it is almost impossible to describe. It is familiar, not simple, and we just have given a label to it ("the American system") that lets us refer to it in a few words. Systems like Quadratic Voting, or ranked choice voting, are often described as complex, but this seems to have more to do with lack of familiarity than complexity. Many scientific concepts, such as the "light cone", are the simplest thing possible once one understands special relativity and yet are utterly foreign and bizarre without having wrapped one's hands around this theory. Even Kolmogorov complexity (length of the shortest computer program that encodes some given system) is relative to some programming language. Now, to some extent, VC dimension offers a solution: it says that a class of systems is simple if it is not too flexible. But consider what happens when you try to apply this; to do so, let's return to our example upfront about Harberger taxes v. perpetual licenses for spectrum.Harberger taxes strike us as quite simple: there is a single tax rate (and the theory even says this is tied down by the rate at which assets turnover, at least if we want to maximally favor allocative efficiency) and the system can be described in a sentence or two. It seems pretty clear that such a system could not be contorted to achieve arbitrary ends. However, an opponent could claim that we chose the Harberger tax from an array of millions of possible mechanisms of a similar class to achieve a specific objective, and it just sounds simple (as with our examples of "deceptive" simplicity above).To counter this argument, we would respond that the Harberger tax, or very similar ideas, have been repeatedly discovered or used (to some success) throughout human history, beginning with the Greeks, and that we do not propose this system simply for spectrum licenses but in a wide range of contexts. The chances that in all these contexts we are cherry-picking the system to "fit" that setting seems low. We would submit to the critic to judge whether it is really plausible that all these historical circumstances and these wide range of applications just "happen" to coincide.Focusing on familiarity (ie. conservatism), rather than simplicity in some abstract mathematical sense, also carries many of the benefits of simplicity as we described above; after all, familiarity is simplicity, if the language we are using to describe ideas includes references to our shared historical experience. Familiar mechanisms also have the benefit that we have more knowledge of how similar ideas historically worked in practice. So why not just be conservative, and favor perpetual property licenses strongly over Harberger taxes?There are three flaws in that logic, it seems to us. First, to the extent it is applied, it should be applied uniformly to all innovation, not merely to new social institutions. Technologies like the internet have contributed greatly to human progress, but have also led to significant social upheavals; this is not a reason to stop trying to advance our technologies and systems for communication, and it is not a reason to stop trying to advance our social technologies for allocating scarce resources.Second, the benefits of innovation are real, and social institutions stand to benefit from growing human intellectual progress as much as everything else. The theoretical case for Harberger taxes providing efficiency benefits is strong, and there is great social value in doing small and medium-scale experiments to try ideas like them out. Investing in experiments today increases what we know, and so increases the scope of what can be done "conservatively" tomorrow.Third, and most importantly, the cultural context in which you as a decision maker have grown up today is far from the only culture that has existed on earth. Even at present, Singapore, China, Taiwan and Scandinavia have had significant success with quite different property regimes than the United States. Video game developers and internet protocol designers have had to solve incentive problems of a similar character to what we see today in the blockchain space and have come up with many kinds of solutions, and throughout history, we have seen a wide variety of social systems used for different purposes, with a wide range of resulting outcomes. By learning about the different ways in which societies have lived, understood what is natural and imagined their politics, we can gain the benefits of learning from historical experience and yet at the same time open ourselves to a much broader space of possible ideas to work with.This is why we believe that balance and collaboration between different modes of learning and understanding, both the mathematical one of economists and computer scientists, and the historical experiences studied by historians, anthropologists, political scientists, etc is critical to avoid the mix of and often veering between extreme conservatism and dangerous utopianism that has become characteristic of much intellectual discourse in e.g. the economics community, the "rationalist" community, and in many cases blockchain protocol design.
[Mirror] Central Planning as Overfitting [Mirror] Central Planning as Overfitting2018 Nov 25 See all posts [Mirror] Central Planning as Overfitting This is a mirror of the post at https://radicalxchange.org/blog/posts/2018-11-26-4m9b8b/ written by myself and Glen WeylThere is an intuition shared by many that "central planning" — command-and-control techniques for allocating resources in economies, and fine-grained knob-turning interventionism more generally — is undesirable. There's quite a lot to this, but it is often misapplied in a way that also leads it to go under-appreciated. In this post we try to clarify the appropriate scope of the intuition.Some recent examples of the intuition being misapplied are:People arguing that relatively simple entitlement programs like Social Security are burdensome government intervention, while elaborate and often discretionary tax breaks conditional on specific behaviors are a good step towards less government. People arguing that block size limits in cryptocurrencies, which impose a hard cap on the number of transactions that each block can contain, are a form of central planning, but who do not argue against other centrally planned parameters, eg. the targeted ten minute (or whatever) average time interval between blocks. People arguing that a lack of block size limits constitutes central planning (!!) People arguing that fixed transaction fees constitute central planning, but variable transaction fees that arise out of an equilibrium itself created by a fixed block size limit do not. We were recently at a discussion in policy circles in Washington, where one of us was arguing for a scheme based on Harberger taxes for spectrum licenses, debating against someone defending more conventional perpetual monopoly licenses on spectrum aggregated at large levels that would tend to create a few national cellular carriers. The latter side argued that the Harberger tax scheme constituted unacceptable bureaucratic interventionism, but seemed to believe that permanent government-issued monopoly privileges are a property right as natural as apples falling from a tree. While we do not entirely dismiss this last example, for reasons we will return to later, it does seem overplayed. Similarly and conversely, we see many examples where, in the name of defending or promoting "markets" (or at least "economic rationality") many professional economists advocate schemes that seem much more to us like central planning than the systems they seek to replace:The most systematic example of this is the literature on "optimal mechanism design," which began with the already extremely complicated and fragile Vickrey-Clarke-Groves mechanism and has only gotten more byzantine from there. While Vickrey's motivation for these ideas was to discover relatively simple rules that would correct the flaws of standard capitalism, he acknowledged in his paper that the design was highly complex in its direct application and urged future researchers to find simplifications. Instead of following this counsel, many scholars have proposed, for example, schemes that rely on a central authority being able to specify an infinite dimensional set of prior beliefs. These schemes, we submit, constitute "central planning" in precisely the sense we should be concerned with. Furthermore, these designs are not just matters of theory, but in practice many applied mechanism designers have created systems with similar properties. The recent United States Spectrum Incentive auctions (designed by a few prominent economists and computer scientists) centralized the enforcement of potential conflicts between transmission rights using an extremely elaborate and opaque computational engine, rather than allowing conflicts to be resolved through (for example) common law liability lawsuits as other interference between property claims and land uses are. A recent design for the allocation of courses to students at the University of Pennsylvania designed by a similar team requires students to express their preferences over courses on a novel numerical scale, allowing them only narrow language for expressing complementarities and substitutability between courses and then uses a state-of-the-art optimization engine to allocate courses. Auction systems designed by economists and computer scientists at large technology companies, like Facebook and Google, are even richer and less transparent, and have created substantial backlash, inspiring a whole industry of firms that help advertisers optimize their bidding in elaborate ways against these systems. This problem does not merely arise in mechanism design, however. In the fields of industrial organization (the basis of much antitrust economics) and the field of macroeconomics (the basis of much monetary policy), extremely elaborate models with hundreds of parameters are empirically estimated and used to simulate the effects of mergers or changes in monetary policy. These models are usually difficult to explain even to experts in the field, much less democratically-elected politicians, judges or, god forbid, voters. And yet the confidence we have in these models, the empirical evidence validating their accuracy, etc. is almost nothing. Nonetheless, economists consistently promote such methods as "the state of the art" and they are generally viewed positively by defenders of the "market economy". To understand why we think the concept of "intervention" is being misapplied here, we need to understand two different ways of measuring the extent to which some scheme is "interventionist". The first approach is to try to measure the absolute magnitude of distortion relative to some imagined state of nature (anarcho-primitivism, or a blockchain with no block size limits, or...). However, this approach clearly fails to capture the intuitions of why central planning is undesirable. For example, property rights in the physical world are a large intervention into almost every person's behavior, considerably limiting the actions that we can take every day. Many of these restrictions are actually of quite recent historical provenance (beginning with agriculture, and mostly in the West and not the East or Middle East). However, opponents of central planning often tend to be the strongest proponents of property rights!We can shed some light on this puzzle by looking at another way of measuring the "central-planny-ness" of some social structure: in short, measure the number of knobs. Property rights actually score quite well here: every piece of property is allocated to some person or legal entity, they can use it as they wish, and no one else can touch it without their permission. There are choices to make around the edges (eg. adverse possession rights), but generally there isn't too much room for changing the scheme around (though note that privatization schemes, ie. transitions from something other than property rights to property rights like the auctions we discussed above, have very many knobs, and so there we can see more risks). Command-and-control regulations with ten thousand clauses (or market designs that specify elaborate probabilistic objects, or optimization protocols, etc.), or attempts to limit use of specific features of the blockchain to drive out specific categories of users, are much less desirable, as such strategies leave many more choices to central planners. A block size limit and a fixed transaction fee (or carbon taxes and a cap-and-trade scheme) have the exact same level of "central-planny-ness" to them: one variable (either quantity or price) is fixed in the protocol, and the other variable is left to the market.Here are some key underlying reasons why we believe that simple social systems with fewer knobs are so desirable:They have fewer moving parts that can fail or otherwise have unexpected effects. They are less likely to overfit. If a social system is too complex, there are many parameters to set and relatively few experiences to draw from when setting the parameters, making it more likely that the parameters will be set to overfit to one context, and generalize poorly to other places or to future times. We know little, and we should not design systems that demand us to know a lot. They are more resistant to corruption. If a social system is simpler, it is more difficult (not impossible, but still more difficult) to set parameters in ways that encode attempts to privilege or anti-privilege specific individuals, factions or communities. This is not only good because it leads to fairness, it is also good because it leads to less zero-sum conflict. They can more easily achieve legitimacy. Because simpler systems are easier to understand, and easier for people to understand that a given implementation is not unfairly privileging special interests, it is easier to create common knowledge that the system is fair, creating a stronger sense of trust. Legitimacy is perhaps the central virtue of social institutions, as it sustains cooperation and coordination, enables the possibility of democracy (how can you democratically participate and endorse a system you do not understand?) and allows for a bottoms-up, rather than top-down, creation of a such a system, ensuring it can be implemented without much coercion or violence. These effects are not always achieved (for example, even if a system has very few knobs, it's often the case that there exists a knob that can be turned to privilege well-connected and wealthy people as a class over everyone else), but the simpler a system is, the more likely the effects are to be achieved.While avoiding over-complexity and overfit in personal decision-making is also important, avoiding these issues in large-scale social systems is even more important, because of the inevitable possibility of powerful forces attempting to manipulate knobs for the benefit of special interests, and the need to achieve common knowledge that the system has not been greatly corrupted, to the point where the fairness of the system is obvious even to unsophisticated observers.This is not to condemn all forms or uses of complexity in social systems. Most science and the inner workings of many technical systems are likely to be opaque to the public but this does not mean science or technology is useless in social life; far from it. However, these systems, to gain legitimacy, usually show that they can reliably achieve some goal, which is transparent and verifiable. Planes land safely and on time, computational systems seem to deliver calculations that are correct, etc. It is by this process of verification, rather than by the transparency of the system per se, that such systems gain their legitimacy. However, for many social systems, truly large-scale, repeatable tests are difficult if not impossible. As such, simplicity is usually critical to legitimacy.Different Notions of SimplicityHowever, there is one class of social systems that seem to be desirable, and that intellectual advocates of minimizing central planning tend to agree are desirable, that don't quite fit the simple "few knobs" characterization that we made above. For example, consider common law. Common law is built up over thousands of precedents, and contains a large number of concepts (eg. see this list under "property law", itself only a part of common law; have you heard of "quicquid plantatur solo, solo cedit" before?). However, proponents of private property are very frequently proponents of common law. So what gives?Here, we need to make a distinction between redundant complexity, or many knobs that really all serve a relatively small number of similar goals, and optimizing complexity, in the extreme one knob per problem that the system has encountered. In computational complexity theory, we typically talk about Kolmogorov complexity, but there are other notions of complexity that are also useful here, particularly VC dimension - roughly, the size of the largest set of situations for which we can turn the knobs in a particular way to achieve any particular set of outcomes. Many successful machine learning techniques, such as Support Vector Machines and Boosting, are quite complex, both in the formal Kolmogorov sense and in terms of the outcomes they produce, but can be proven to have low VC dimension.VC dimension does a nice job capturing some of the arguments for simplicity mentioned above more explicitly, for example:A system with low VC dimension may have some moving parts that fail, but if it does, its different constituent parts can correct for each other. By construction, it has built in resilience through redundancy Low VC dimension is literally a measure of resistance to overfit. Low VC dimension leads to resistance to corruption, because if VC dimension is low, a corrupt or self-interested party in control of some knobs will not as easily be able to achieve some particular outcome that they desire. In particular, this agent will be "checked and balanced" by other parts of the system that redundantly achieve the originally desired ends. They can achieve legitimacy because people can randomly check a few parts and verify in detail that those parts work in ways that are reasonable, and assume that the rest of the system works in a similar way. An example of this was the ratification of the United States Constitution which, while quite elaborate, was primarily elaborate in the redundancy with which it applied the principle of checks and balances of power. Thus most citizens only read one or a few of The Federalist Papers that explained and defended the Constitution, and yet got a reasonable sense for what was going on. This is not as clean and convenient as a system with low Kolmogorov complexity, but still much better than a system with high complexity where the complexity is "optimizing" (for an example of this in the blockchain context, see Vitalik's opposition and alternative to on-chain governance). The primary disadvantage we see in Kolmogorov complex but VC simple designs is for new social institutions, where it may be hard to persuade the public that these are VC simple. VC simplicity is usually easier as a basis for legitimacy when an institutions has clearly been built up without any clear design over a long period of time or by a large committee of people with conflicting interests (as with the United States Constitution). Thus when offering innovations we tend to focus more on Kolmogorov simplicity and hope many redundant each Kolmogorov-simple elements will add up to a VC-simple system. However, we may just not have the imagination to think of how VC simplicity might be effectively explained.There are forms of the "avoid central planning" intuition that are misunderstandings and ultimately counterproductive. For example, try to automatically seize upon designs that seem at first glance to "look like a market", because not all markets are created equal. For example, one of us has argued for using fixed prices in certain settings to reduce uncertainty, and the other has (for similar information sharing reasons) argued for auctions that are a synthesis of standard descending price Dutch and ascending price English auctions (Channel auctions). That said, it is also equally a large error to throw the intuition away entirely. Rather, it is a valuable and important insight that can easily is central to the methodology we have been recently trying to develop. Simplicity to Whom? Or Why Humanities MatterHowever, the academic critics of this type of work are not simply confused. There is a reasonable basis for unease with discussions of "simplicity" because they inevitably contain a degree of subjectivity. What is "simple" to describe or appears to have few knobs in one language for describing it is devilishly complex in another, and vice versa. A few examples should help illuminate the point:We have repeatedly referred to "knobs", which are roughly real valued parameters. But real-valued parameters can encode an arbitrary amount of complexity. For example, I could claim my system has only one knob, it is just that slight changes in the 1000th decimal place of the setting of that knob end up determining incredibly important properties of the system. This may seem cheap, but more broadly it is the case that non-linear mappings between systems can make one system seem "simple" and another "complex" and in general there is just no way to say which is right. Many think of the electoral system of the United States as "simple", and yet, if one reflects on it or tries to explain it to a foreigner, it is almost impossible to describe. It is familiar, not simple, and we just have given a label to it ("the American system") that lets us refer to it in a few words. Systems like Quadratic Voting, or ranked choice voting, are often described as complex, but this seems to have more to do with lack of familiarity than complexity. Many scientific concepts, such as the "light cone", are the simplest thing possible once one understands special relativity and yet are utterly foreign and bizarre without having wrapped one's hands around this theory. Even Kolmogorov complexity (length of the shortest computer program that encodes some given system) is relative to some programming language. Now, to some extent, VC dimension offers a solution: it says that a class of systems is simple if it is not too flexible. But consider what happens when you try to apply this; to do so, let's return to our example upfront about Harberger taxes v. perpetual licenses for spectrum.Harberger taxes strike us as quite simple: there is a single tax rate (and the theory even says this is tied down by the rate at which assets turnover, at least if we want to maximally favor allocative efficiency) and the system can be described in a sentence or two. It seems pretty clear that such a system could not be contorted to achieve arbitrary ends. However, an opponent could claim that we chose the Harberger tax from an array of millions of possible mechanisms of a similar class to achieve a specific objective, and it just sounds simple (as with our examples of "deceptive" simplicity above).To counter this argument, we would respond that the Harberger tax, or very similar ideas, have been repeatedly discovered or used (to some success) throughout human history, beginning with the Greeks, and that we do not propose this system simply for spectrum licenses but in a wide range of contexts. The chances that in all these contexts we are cherry-picking the system to "fit" that setting seems low. We would submit to the critic to judge whether it is really plausible that all these historical circumstances and these wide range of applications just "happen" to coincide.Focusing on familiarity (ie. conservatism), rather than simplicity in some abstract mathematical sense, also carries many of the benefits of simplicity as we described above; after all, familiarity is simplicity, if the language we are using to describe ideas includes references to our shared historical experience. Familiar mechanisms also have the benefit that we have more knowledge of how similar ideas historically worked in practice. So why not just be conservative, and favor perpetual property licenses strongly over Harberger taxes?There are three flaws in that logic, it seems to us. First, to the extent it is applied, it should be applied uniformly to all innovation, not merely to new social institutions. Technologies like the internet have contributed greatly to human progress, but have also led to significant social upheavals; this is not a reason to stop trying to advance our technologies and systems for communication, and it is not a reason to stop trying to advance our social technologies for allocating scarce resources.Second, the benefits of innovation are real, and social institutions stand to benefit from growing human intellectual progress as much as everything else. The theoretical case for Harberger taxes providing efficiency benefits is strong, and there is great social value in doing small and medium-scale experiments to try ideas like them out. Investing in experiments today increases what we know, and so increases the scope of what can be done "conservatively" tomorrow.Third, and most importantly, the cultural context in which you as a decision maker have grown up today is far from the only culture that has existed on earth. Even at present, Singapore, China, Taiwan and Scandinavia have had significant success with quite different property regimes than the United States. Video game developers and internet protocol designers have had to solve incentive problems of a similar character to what we see today in the blockchain space and have come up with many kinds of solutions, and throughout history, we have seen a wide variety of social systems used for different purposes, with a wide range of resulting outcomes. By learning about the different ways in which societies have lived, understood what is natural and imagined their politics, we can gain the benefits of learning from historical experience and yet at the same time open ourselves to a much broader space of possible ideas to work with.This is why we believe that balance and collaboration between different modes of learning and understanding, both the mathematical one of economists and computer scientists, and the historical experiences studied by historians, anthropologists, political scientists, etc is critical to avoid the mix of and often veering between extreme conservatism and dangerous utopianism that has become characteristic of much intellectual discourse in e.g. the economics community, the "rationalist" community, and in many cases blockchain protocol design.


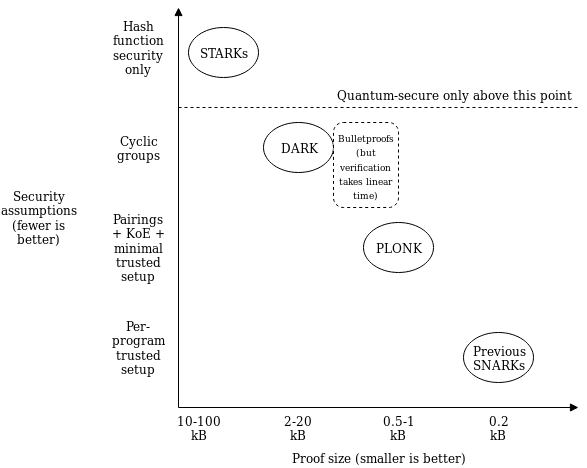
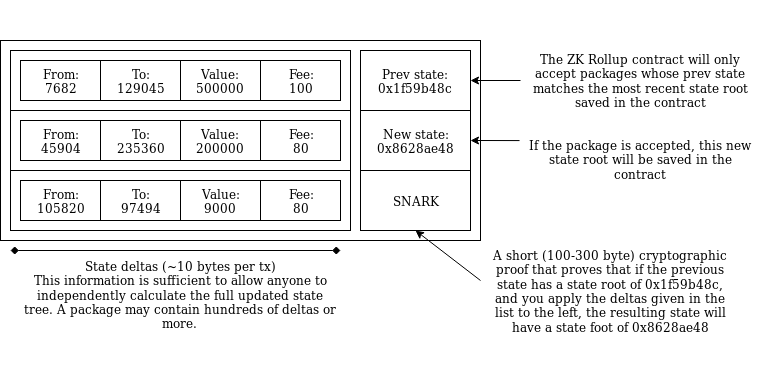
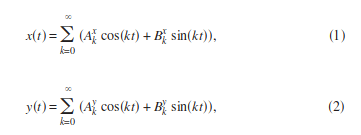

![[Mirror] Cantor was Wrong: debunking the infinite set hierarchy](https://cdn-images-1.medium.com/max/2000/1*4ByVTuO_nU-lKZo7NHDBWA.png)