heyuan 发布的文章 - 六币之门

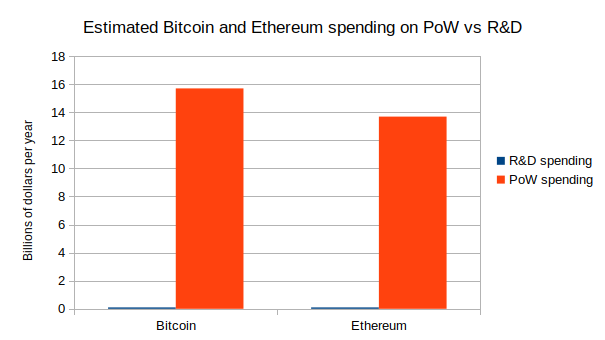
Moving beyond coin voting governance Moving beyond coin voting governance2021 Aug 16 See all posts Moving beyond coin voting governance Special thanks to Karl Floersch, Dan Robinson and Tina Zhen for feedback and review. See also Notes on Blockchain Governance, Governance, Part 2: Plutocracy Is Still Bad, On Collusion and Coordination, Good and Bad for earlier thinking on similar topics.One of the important trends in the blockchain space over the past year is the transition from focusing on decentralized finance (DeFi) to also thinking about decentralized governance (DeGov). While the 2020 is often widely, and with much justification, hailed as a year of DeFi, over the year since then the growing complexity and capability of DeFi projects that make up this trend has led to growing interest in decentralized governance to handle that complexity. There are examples inside of Ethereum: YFI, Compound, Synthetix, UNI, Gitcoin and others have all launched, or even started with, some kind of DAO. But it's also true outside of Ethereum, with arguments over infrastructure funding proposals in Bitcoin Cash, infrastructure funding votes in Zcash, and much more.The rising popularity of formalized decentralized governance of some form is undeniable, and there are important reasons why people are interested in it. But it is also important to keep in mind the risks of such schemes, as the recent hostile takeover of Steem and subsequent mass exodus to Hive makes clear. I would further argue that these trends are unavoidable. Decentralized governance in some contexts is both necessary and dangerous, for reasons that I will get into in this post. How can we get the benefits of DeGov while minimizing the risks? I will argue for one key part of the answer: we need to move beyond coin voting as it exists in its present form.DeGov is necessaryEver since the Declaration of Independence of Cyberspace in 1996, there has been a key unresolved contradiction in what can be called cypherpunk ideology. On the one hand, cypherpunk values are all about using cryptography to minimize coercion, and maximize the efficiency and reach of the main non-coercive coordination mechanism available at the time: private property and markets. On the other hand, the economic logic of private property and markets is optimized for activities that can be "decomposed" into repeated one-to-one interactions, and the infosphere, where art, documentation, science and code are produced and consumed through irreducibly one-to-many interactions, is the exact opposite of that.There are two key problems inherent to such an environment that need to be solved:Funding public goods: how do projects that are valuable to a wide and unselective group of people in the community, but which often do not have a business model (eg. layer-1 and layer-2 protocol research, client development, documentation...), get funded? Protocol maintenance and upgrades: how are upgrades to the protocol, and regular maintenance and adjustment operations on parts of the protocol that are not long-term stable (eg. lists of safe assets, price oracle sources, multi-party computation keyholders), agreed upon? Early blockchain projects largely ignored both of these challenges, pretending that the only public good that mattered was network security, which could be achieved with a single algorithm set in stone forever and paid for with fixed proof of work rewards. This state of affairs in funding was possible at first because of extreme Bitcoin price rises from 2010-13, then the one-time ICO boom from 2014-17, and again from the simultaneous second crypto bubble of 2014-17, all of which made the ecosystem wealthy enough to temporarily paper over the large market inefficiencies. Long-term governance of public resources was similarly ignored: Bitcoin took the path of extreme minimization, focusing on providing a fixed-supply currency and ensuring support for layer-2 payment systems like Lightning and nothing else, Ethereum continued developing mostly harmoniously (with one major exception) because of the strong legitimacy of its pre-existing roadmap (basically: "proof of stake and sharding"), and sophisticated application-layer projects that required anything more did not yet exist.But now, increasingly, that luck is running out, and challenges of coordinating protocol maintenance and upgrades and funding documentation, research and development while avoiding the risks of centralization are at the forefront.The need for DeGov for funding public goodsIt is worth stepping back and seeing the absurdity of the present situation. Daily mining issuance rewards from Ethereum are about 13500 ETH, or about $40m, per day. Transaction fees are similarly high; the non-EIP-1559-burned portion continues to be around 1,500 ETH (~$4.5m) per day. So there are many billions of dollars per year going to fund network security. Now, what is the budget of the Ethereum Foundation? About $30-60 million per year. There are non-EF actors (eg. Consensys) contributing to development, but they are not much larger. The situation in Bitcoin is similar, with perhaps even less funding going into non-security public goods.Here is the situation in a chart:Within the Ethereum ecosystem, one can make a case that this disparity does not matter too much; tens of millions of dollars per year is "enough" to do the needed R&D and adding more funds does not necessarily improve things, and so the risks to the platform's credible neutrality from instituting in-protocol developer funding exceed the benefits. But in many smaller ecosystems, both ecosystems within Ethereum and entirely separate blockchains like BCH and Zcash, the same debate is brewing, and at those smaller scales the imbalance makes a big difference.Enter DAOs. A project that launches as a "pure" DAO from day 1 can achieve a combination of two properties that were previously impossible to combine: (i) sufficiency of developer funding, and (ii) credible neutrality of funding (the much-coveted "fair launch"). Instead of developer funding coming from a hardcoded list of receiving addresses, the decisions can be made by the DAO itself.Of course, it's difficult to make a launch perfectly fair, and unfairness from information asymmetry can often be worse than unfairness from explicit premines (was Bitcoin really a fair launch considering how few people had a chance to even hear about it by the time 1/4 of the supply had already been handed out by the end of 2010?). But even still, in-protocol compensation for non-security public goods from day one seems like a potentially significant step forward toward getting sufficient and more credibly neutral developer funding.The need for DeGov for protocol maintenance and upgradesIn addition to public goods funding, the other equally important problem requiring governance is protocol maintenance and upgrades. While I advocate trying to minimize all non-automated parameter adjustment (see the "limited governance" section below) and I am a fan of RAI's "un-governance" strategy, there are times where governance is unavoidable. Price oracle inputs must come from somewhere, and occasionally that somewhere needs to change. Until a protocol "ossifies" into its final form, improvements have to be coordinated somehow. Sometimes, a protocol's community might think that they are ready to ossify, but then the world throws a curveball that requires a complete and controversial restructuring. What happens if the US dollar collapses, and RAI has to scramble to create and maintain their own decentralized CPI index for their stablecoin to remain stable and relevant? Here too, DeGov is necessary, and so avoiding it outright is not a viable solution.One important distinction is whether or not off-chain governance is possible. I have for a long time been a fan of off-chain governance wherever possible. And indeed, for base-layer blockchains, off-chain governance absolutely is possible. But for application-layer projects, and especially defi projects, we run into the problem that application-layer smart contract systems often directly control external assets, and that control cannot be forked away. If Tezos's on-chain governance gets captured by an attacker, the community can hard-fork away without any losses beyond (admittedly high) coordination costs. If MakerDAO's on-chain governance gets captured by an attacker, the community can absolutely spin up a new MakerDAO, but they will lose all the ETH and other assets that are stuck in the existing MakerDAO CDPs. Hence, while off-chain governance is a good solution for base layers and some application-layer projects, many application-layer projects, particularly DeFi, will inevitably require formalized on-chain governance of some form.DeGov is dangerousHowever, all current instantiations of decentralized governance come with great risks. To followers of my writing, this discussion will not be new; the risks are much the same as those that I talked about here, here and here. There are two primary types of issues with coin voting that I worry about: (i) inequalities and incentive misalignments even in the absence of attackers, and (ii) outright attacks through various forms of (often obfuscated) vote buying. To the former, there have already been many proposed mitigations (eg. delegation), and there will be more. But the latter is a much more dangerous elephant in the room to which I see no solution within the current coin voting paradigm.Problems with coin voting even in the absence of attackersThe problems with coin voting even without explicit attackers are increasingly well-understood (eg. see this recent piece by DappRadar and Monday Capital), and mostly fall into a few buckets:Small groups of wealthy participants ("whales") are better at successfully executing decisions than large groups of small-holders. This is because of the tragedy of the commons among small-holders: each small-holder has only an insignificant influence on the outcome, and so they have little incentive to not be lazy and actually vote. Even if there are rewards for voting, there is little incentive to research and think carefully about what they are voting for. Coin voting governance empowers coin holders and coin holder interests at the expense of other parts of the community: protocol communities are made up of diverse constituencies that have many different values, visions and goals. Coin voting, however, only gives power to one constituency (coin holders, and especially wealthy ones), and leads to over-valuing the goal of making the coin price go up even if that involves harmful rent extraction. Conflict of interest issues: giving voting power to one constituency (coin holders), and especially over-empowering wealthy actors in that constituency, risks over-exposure to the conflicts-of-interest within that particular elite (eg. investment funds or holders that also hold tokens of other DeFi platforms that interact with the platform in question) There is one major type of strategy being attempted for solving the first problem (and therefore also mitigating the third problem): delegation. Smallholders don't have to personally judge each decision; instead, they can delegate to community members that they trust. This is an honorable and worthy experiment; we shall see how well delegation can mitigate the problem. My voting delegation page in the Gitcoin DAOThe problem of coin holder centrism, on the other hand, is significantly more challenging: coin holder centrism is inherently baked into a system where coin holder votes are the only input. The mis-perception that coin holder centrism is an intended goal, and not a bug, is already causing confusion and harm; one (broadly excellent) article discussing blockchain public goods complains:Can crypto protocols be considered public goods if ownership is concentrated in the hands of a few whales? Colloquially, these market primitives are sometimes described as "public infrastructure," but if blockchains serve a "public" today, it is primarily one of decentralized finance. Fundamentally, these tokenholders share only one common object of concern: price.The complaint is false; blockchains serve a public much richer and broader than DeFi token holders. But our coin-voting-driven governance systems are completely failing to capture that, and it seems difficult to make a governance system that captures that richness without a more fundamental change to the paradigm.Coin voting's deep fundamental vulnerability to attackers: vote buyingThe problems get much worse once determined attackers trying to subvert the system enter the picture. The fundamental vulnerability of coin voting is simple to understand. A token in a protocol with coin voting is a bundle of two rights that are combined into a single asset: (i) some kind of economic interest in the protocol's revenue and (ii) the right to participate in governance. This combination is deliberate: the goal is to align power and responsibility. But in fact, these two rights are very easy to unbundle from each other. Imagine a simple wrapper contract that has these rules: if you deposit 1 XYZ into the contract, you get back 1 WXYZ. That WXYZ can be converted back into an XYZ at any time, plus in addition it accrues dividends. Where do the dividends come from? Well, while the XYZ coins are inside the wrapper contract, it's the wrapper contract that has the ability to use them however it wants in governance (making proposals, voting on proposals, etc). The wrapper contract simply auctions off this right every day, and distributes the profits among the original depositors. As an XYZ holder, is it in your interest to deposit your coins into the contract? If you are a very large holder, it might not be; you like the dividends, but you are scared of what a misaligned actor might do with the governance power you are selling them. But if you are a smaller holder, then it very much is. If the governance power auctioned by the wrapper contract gets bought up by an attacker, you personally only suffer a small fraction of the cost of the bad governance decisions that your token is contributing to, but you personally gain the full benefit of the dividend from the governance rights auction. This situation is a classic tragedy of the commons.Suppose that an attacker makes a decision that corrupts the DAO to the attacker's benefit. The harm per participant from the decision succeeding is \(D\), and the chance that a single vote tilts the outcome is \(p\). Suppose an attacker makes a bribe of \(B\). The game chart looks like this: Decision Benefit to you Benefit to others Accept attacker's bribe \(B - D * p\) \(-999 * D * p\) Reject bribe, vote your conscience \(0\) \(0\) If \(B > D * p\), you are inclined to accept the bribe, but as long as \(B < 1000 * D * p\), accepting the bribe is collectively harmful. So if \(p < 1\) (usually, \(p\) is far below \(1\)), there is an opportunity for an attacker to bribe users to adopt a net-negative decision, compensating each user far less than the harm they suffer.One natural critique of voter bribing fears is: are voters really going to be so immoral as to accept such obvious bribes? The average DAO token holder is an enthusiast, and it would be hard for them to feel good about so selfishly and blatantly selling out the project. But what this misses is that there are much more obfuscated ways to separate out profit sharing rights from governance rights, that don't require anything remotely as explicit as a wrapper contract.The simplest example is borrowing from a defi lending platform (eg. Compound). Someone who already holds ETH can lock up their ETH in a CDP ("collateralized debt position") in one of these platforms, and once they do that the CDP contract allows them to borrow an amount of XYZ up to eg. half the value of the ETH that they put in. They can then do whatever they want with this XYZ. To recover their ETH, they would eventually need to pay back the XYZ that they borrowed, plus interest. Note that throughout this process, the borrower has no financial exposure to XYZ. That is, if they use their XYZ to vote for a governance decision that destroys the value of XYZ, they do not lose a penny as a result. The XYZ they are holding is XYZ that they have to eventually pay back into the CDP regardless, so they do not care if its value goes up or down. And so we have achieved unbundling: the borrower has governance power without economic interest, and the lender has economic interest without governance power.There are also centralized mechanisms for separating profit sharing rights from governance rights. Most notably, when users deposit their coins on a (centralized) exchange, the exchange holds full custody of those coins, and the exchange has the ability to use those coins to vote. This is not mere theory; there is evidence of exchanges using their users' coins in several DPoS systems. The most notable recent example is the attempted hostile takeover of Steem, where exchanges used their customers' coins to vote for some proposals that helped to cement a takeover of the Steem network that the bulk of the community strongly opposed. The situation was only resolved through an outright mass exodus, where a large portion of the community moved to a different chain called Hive.Some DAO protocols are using timelock techniques to limit these attacks, requiring users to lock their coins and make them immovable for some period of time in order to vote. These techniques can limit buy-then-vote-then-sell attacks in the short term, but ultimately timelock mechanisms can be bypassed by users holding and voting with their coins through a contract that issues a wrapped version of the token (or, more trivially, a centralized exchange). As far as security mechanisms go, timelocks are more like a paywall on a newspaper website than they are like a lock and key.At present, many blockchains and DAOs with coin voting have so far managed to avoid these attacks in their most severe forms. There are occasional signs of attempted bribes: But despite all of these important issues, there have been much fewer examples of outright voter bribing, including obfuscated forms such as using financial markets, that simple economic reasoning would suggest. The natural question to ask is: why haven't more outright attacks happened yet?My answer is that the "why not yet" relies on three contingent factors that are true today, but are likely to get less true over time:Community spirit from having a tightly-knit community, where everyone feels a sense of camaraderie in a common tribe and mission.. High wealth concentration and coordination of token holders; large holders have higher ability to affect the outcome and have investments in long-term relationships with each other (both the "old boys clubs" of VCs, but also many other equally powerful but lower-profile groups of wealthy token holders), and this makes them much more difficult to bribe. Immature financial markets in governance tokens: ready-made tools for making wrapper tokens exist in proof-of-concept forms but are not widely used, bribing contracts exist but are similarly immature, and liquidity in lending markets is low. When a small coordinated group of users holds over 50% of the coins, and both they and the rest are invested in a tightly-knit community, and there are few tokens being lent out at reasonable rates, all of the above bribing attacks may perhaps remain theoretical. But over time, (1) and (3) will inevitably become less true no matter what we do, and (2) must become less true if we want DAOs to become more fair. When those changes happen, will DAOs remain safe? And if coin voting cannot be sustainably resistant against attacks, then what can?Solution 1: limited governanceOne possible mitigation to the above issues, and one that is to varying extents being tried already, is to put limits on what coin-driven governance can do. There are a few ways to do this:Use on-chain governance only for applications, not base layers: Ethereum does this already, as the protocol itself is governed through off-chain governance, while DAOs and other apps on top of this are sometimes (but not always) governed through on-chain governance Limit governance to fixed parameter choices: Uniswap does this, as it only allows governance to affect (i) token distribution and (ii) a 0.05% fee in the Uniswap exchange. Another great example is RAI's "un-governance" roadmap, where governance has control over fewer and fewer features over time. Add time delays: a governance decision made at time T only takes effect at eg. T + 90 days. This allows users and applications that consider the decision unacceptable to move to another application (possibly a fork). Compound has a time delay mechanism in its governance, but in principle the delay can (and eventually should) be much longer. Be more fork-friendly: make it easier for users to quickly coordinate on and execute a fork. This makes the payoff of capturing governance smaller. The Uniswap case is particularly interesting: it's an intended behavior that the on-chain governance funds teams, which may develop future versions of the Uniswap protocol, but it's up to users to opt-in to upgrading to those versions. This is a hybrid of on-chain and off-chain governance that leaves only a limited role for the on-chain side.But limited governance is not an acceptable solution by itself; those areas where governance is needed the most (eg. funds distribution for public goods) are themselves among the most vulnerable to attack. Public goods funding is so vulnerable to attack because there is a very direct way for an attacker to profit from bad decisions: they can try to push through a bad decision that sends funds to themselves. Hence, we also need techniques to improve governance itself...Solution 2: non-coin-driven governanceA second approach is to use forms of governance that are not coin-voting-driven. But if coins do not determine what weight an account has in governance, what does? There are two natural alternatives:Proof of personhood systems: systems that verify that accounts correspond to unique individual humans, so that governance can assign one vote per human. See here for a review of some techniques being developed, and ProofOfHumanity and BrightID and Idenanetwork for three attempts to implement this. Proof of participation: systems that attest to the fact that some account corresponds to a person that has participated in some event, passed some educational training, or performed some useful work in the ecosystem. See POAP for one attempt to implement thus. There are also hybrid possibilities: one example is quadratic voting, which makes the power of a single voter proportional to the square root of the economic resources that they commit to a decision. Preventing people from gaming the system by splitting their resource across many identities requires proof of personhood, and the still-existent financial component allows participants to credibly signal how strongly they care about an issue, as well as how strongly they care about the ecosystem. Gitcoin quadratic funding is a form of quadratic voting, and quadratic voting DAOs are being built.Proof of participation is less well-understood. The key challenge is that determining what counts as how much participation itself requires a quite robust governance structure. It's possible that the easiest solution involves bootstrapping the system with a hand-picked choice of 10-100 early contributors, and then decentralizing over time as the selected participants of round N determine participation criteria for round N+1. The possibility of a fork helps provide a path to recovery from, and an incentive against, governance going off the rails.Proof of personhood and proof of participation both require some form of anti-collusion (see article explaining the issue here and MACI documentation here) to ensure that the non-money resource being used to measure voting power remains non-financial, and does not itself end up inside of smart contracts that sell the governance power to the highest bidder.Solution 3: skin in the gameThe third approach is to break the tragedy of the commons, by changing the rules of the vote itself. Coin voting fails because while voters are collectively accountable for their decisions (if everyone votes for a terrible decision, everyone's coins drop to zero), each voter is not individually accountable (if a terrible decision happens, those who supported it suffer no more than those who opposed it). Can we make a voting system that changes this dynamic, and makes voters individually, and not just collectively, responsible for their decisions?Fork-friendliness is arguably a skin-in-the-game strategy, if forks are done in the way that Hive forked from Steem. In the case that a ruinous governance decision succeeds and can no longer be opposed inside the protocol, users can take it upon themselves to make a fork. Furthermore, in that fork, the coins that voted for the bad decision can be destroyed. This sounds harsh, and perhaps it even feels like a violation of an implicit norm that the "immutability of the ledger" should remain sacrosanct when forking a coin. But the idea seems much more reasonable when seen from a different perspective. We keep the idea of a strong firewall where individual coin balances are expected to be inviolate, but only apply that protection to coins that do not participate in governance. If you participate in governance, even indirectly by putting your coins into a wrapper mechanism, then you may be held liable for the costs of your actions.This creates individual responsibility: if an attack happens, and your coins vote for the attack, then your coins are destroyed. If your coins do not vote for the attack, your coins are safe. The responsibility propagates upward: if you put your coins into a wrapper contract and the wrapper contract votes for an attack, the wrapper contract's balance is wiped and so you lose your coins. If an attacker borrows XYZ from a defi lending platform, when the platform forks anyone who lent XYZ loses out (note that this makes lending the governance token in general very risky; this is an intended consequence).Skin-in-the-game in day-to-day votingBut the above only works for guarding against decisions that are truly extreme. What about smaller-scale heists, which unfairly favor attackers manipulating the economics of the governance but not severely enough to be ruinous? And what about, in the absence of any attackers at all, simple laziness, and the fact that coin-voting governance has no selection pressure in favor of higher-quality opinions?The most popular solution to these kinds of issues is futarchy, introduced by Robin Hanson in the early 2000s. Votes become bets: to vote in favor of a proposal, you make a bet that the proposal will lead to a good outcome, and to vote against the proposal, you make a bet that the proposal will lead to a poor outcome. Futarchy introduces individual responsibility for obvious reasons: if you make good bets, you get more coins, and if you make bad bets you lose your coins. "Pure" futarchy has proven difficult to introduce, because in practice objective functions are very difficult to define (it's not just coin price that people want!), but various hybrid forms of futarchy may well work. Examples of hybrid futarchy include:Votes as buy orders: see ethresear.ch post. Voting in favor of a proposal requires making an enforceable buy order to buy additional tokens at a price somewhat lower than the token's current price. This ensures that if a terrible decision succeeds, those who support it may be forced to buy their opponents out, but it also ensures that in more "normal" decisions coin holders have more slack to decide according to non-price criteria if they so wish. Retroactive public goods funding: see post with the Optimism team. Public goods are funded by some voting mechanism retroactively, after they have already achieved a result. Users can buy project tokens to fund their project while signaling confidence in it; buyers of project tokens get a share of the reward if that project is deemed to have achieved a desired goal. Escalation games: see Augur and Kleros. Value-alignment on lower-level decisions is incentivized by the possibility to appeal to a higher-effort but higher-accuracy higher-level process; voters whose votes agree with the ultimate decision are rewarded. In the latter two cases, hybrid futarchy depends on some form of non-futarchy governance to measure against the objective function or serve as a dispute layer of last resort. However, this non-futarchy governance has several advantages that it does not if used directly: (i) it activates later, so it has access to more information, (ii) it is used less frequently, so it can expend less effort, and (iii) each use of it has greater consequences, so it's more acceptable to just rely on forking to align incentives for this final layer.Hybrid solutionsThere are also solutions that combine elements of the above techniques. Some possible examples:Time delays plus elected-specialist governance: this is one possible solution to the ancient conundrum of how to make an crypto-collateralized stablecoin whose locked funds can exceed the value of the profit-taking token without risking governance capture. The stable coin uses a price oracle constructed from the median of values submitted by N (eg. N = 13) elected providers. Coin voting chooses the providers, but it can only cycle out one provider each week. If users notice that coin voting is bringing in untrustworthy price providers, they have N/2 weeks before the stablecoin breaks to switch to a different one. Futarchy + anti-collusion = reputation: Users vote with "reputation", a token that cannot be transferred. Users gain more reputation if their decisions lead to desired results, and lose reputation if their decisions lead to undesired results. See here for an article advocating for a reputation-based scheme. Loosely-coupled (advisory) coin votes: a coin vote does not directly implement a proposed change, instead it simply exists to make its outcome public, to build legitimacy for off-chain governance to implement that change. This can provide the benefits of coin votes, with fewer risks, as the legitimacy of a coin vote drops off automatically if evidence emerges that the coin vote was bribed or otherwise manipulated. But these are all only a few possible examples. There is much more that can be done in researching and developing non-coin-driven governance algorithms. The most important thing that can be done today is moving away from the idea that coin voting is the only legitimate form of governance decentralization. Coin voting is attractive because it feels credibly neutral: anyone can go and get some units of the governance token on Uniswap. In practice, however, coin voting may well only appear secure today precisely because of the imperfections in its neutrality (namely, large portions of the supply staying in the hands of a tightly-coordinated clique of insiders).We should stay very wary of the idea that current forms of coin voting are "safe defaults". There is still much that remains to be seen about how they function under conditions of more economic stress and mature ecosystems and financial markets, and the time is now to start simultaneously experimenting with alternatives.

Against overuse of the Gini coefficient Against overuse of the Gini coefficient2021 Jul 29 See all posts Against overuse of the Gini coefficient Special thanks to Barnabe Monnot and Tina Zhen for feedback and reviewThe Gini coefficient (also called the Gini index) is by far the most popular and widely known measure of inequality, typically used to measure inequality of income or wealth in some country, territory or other community. It's popular because it's easy to understand, with a mathematical definition that can easily be visualized on a graph.However, as one might expect from any scheme that tried to reduce inequality to a single number, the Gini coefficient also has its limits. This is true even in its original context of measuring income and wealth inequality in countries, but it becomes even more true when the Gini coefficient is transplanted into other contexts (particularly: cryptocurrency). In this post I will talk about some of the limits of the Gini coefficient, and propose some alternatives.What is the Gini coefficient?The Gini coefficient is a measure of inequality introduced by Corrado Gini in 1912. It is typically used to measure inequality of income and wealth of countries, though it is also increasingly being used in other contexts.There are two equivalent definitions of the Gini coefficient:Area-above-curve definition: draw the graph of a function, where \(f(p)\) equals the share of total income earned by the lowest-earning portion of the population (eg. \(f(0.1)\) is the share of total income earned by the lowest-earning 10%). The Gini coefficient is the area between that curve and the \(y=x\) line, as a portion of the whole triangle:Average-difference definition: the Gini coefficient is half the average difference of incomes between each all possible pairs of individuals, divided by the mean income.For example, in the above example chart, the four incomes are [1, 2, 4, 8], so the 16 possible differences are [0, 1, 3, 7, 1, 0, 2, 6, 3, 2, 0, 4, 7, 6, 4, 0]. Hence the average difference is 2.875 and the mean income is 3.75, so Gini = \(\frac \approx 0.3833\).It turns out that the two are mathematically equivalent (proving this is an exercise to the reader)!What's wrong with the Gini coefficient?The Gini coefficient is attractive because it's a reasonably simple and easy-to-understand statistic. It might not look simple, but trust me, pretty much everything in statistics that deals with populations of arbitrary size is that bad, and often much worse. Here, stare at the formula of something as basic as the standard deviation:\(\sigma = \frac^n x_i^2} - (\frac^n x_i})^2\)And here's the Gini:\(G = \frac^n i*x_i}^n x_i} - \frac\)It's actually quite tame, I promise!So, what's wrong with it? Well, there are lots of things wrong with it, and people have written lots of articles about various problems with the Gini coefficient. In this article, I will focus on one specific problem that I think is under-discussed about the Gini as a whole, but that has particular relevance to analyzing inequality in internet communities such as blockchains. The Gini coefficient combines together into a single inequality index two problems that actually look quite different: suffering due to lack of resources and concentration of power.To understand the difference between the two problems more clearly, let's look at two dystopias:Dystopia A: half the population equally shares all the resources, everyone else has none Dystopia B: one person has half of all the resources, everyone else equally shares the remaining half Here are the Lorenz curves (fancy charts like we saw above) for both dystopias:Clearly, neither of those two dystopias are good places to live. But they are not-very-nice places to live in very different ways. Dystopia A gives each resident a coin flip between unthinkably horrific mass starvation if they end up on the left half on the distribution and egalitarian harmony if they end up on the right half. If you're Thanos, you might actually like it! If you're not, it's worth avoiding with the strongest force. Dystopia B, on the other hand, is Brave New World-like: everyone has decently good lives (at least at the time when that snapshot of everyone's resources is taken), but at the high cost of an extremely undemocratic power structure where you'd better hope you have a good overlord. If you're Curtis Yarvin, you might actually like it! If you're not, it's very much worth avoiding too.These two problems are different enough that they're worth analyzing and measuring separately. And this difference is not just theoretical. Here is a chart showing share of total income earned by the bottom 20% (a decent proxy for avoiding dystopia A) versus share of total income earned by the top 1% (a decent proxy for being near dystopia B): Sources: https://data.worldbank.org/indicator/SI.DST.FRST.20 (merging 2015 and 2016 data) and http://hdr.undp.org/en/indicators/186106.The two are clearly correlated (coefficient -0.62), but very far from perfectly correlated (the high priests of statistics apparently consider 0.7 to be the lower threshold for being "highly correlated", and we're even under that). There's an interesting second dimension to the chart that can be analyzed - what's the difference between a country where the top 1% earn 20% of the total income and the bottom 20% earn 3% and a country where the top 1% earn 20% and the bottom 20% earn 7%? Alas, such an exploration is best left to other enterprising data and culture explorers with more experience than myself.Why Gini is very problematic in non-geographic communities (eg. internet/crypto communities)Wealth concentration within the blockchain space in particular is an important problem, and it's a problem worth measuring and understanding. It's important for the blockchain space as a whole, as many people (and US senate hearings) are trying to figure out to what extent crypto is truly anti-elitist and to what extent it's just replacing old elites with new ones. It's also important when comparing different cryptocurrencies with each other. Share of coins explicitly allocated to specific insiders in a cryptocurrency's initial supply is one type of inequality. Note that the Ethereum data is slightly wrong: the insider and foundation shares should be 12.3% and 4.2%, not 15% and 5%.Given the level of concern about these issues, it should be not at all surprising that many people have tried computing Gini indices of cryptocurrencies:The observed Gini index for staked EOS tokens (2018) Gini coefficients of cryptocurrencies (2018) Measuring decentralization in Bitcoin and Ethereum using Multiple Metrics and Granularities (2021, includes Gini and 2 other metrics) Nouriel Roubini comparing Bitcoin's Gini to North Korea (2018) On-chain Insights in the Cryptocurrency Markets (2021, uses Gini to measure concentration) And even earlier than that, we had to deal with this sensationalist article from 2014:In addition to common plain methodological mistakes (often either mixing up income vs wealth inequality, mixing up users vs accounts, or both) that such analyses make quite frequently, there is a deep and subtle problem with using the Gini coefficient to make these kinds of comparisons. The problem lies in key distinction between typical geographic communities (eg. cities, countries) and typical internet communities (eg. blockchains):A typical resident of a geographic community spends most of their time and resources in that community, and so measured inequality in a geographic community reflects inequality in total resources available to people. But in an internet community, measured inequality can come from two sources: (i) inequality in total resources available to different participants, and (ii) inequality in level of interest in participating in the community.The average person with $15 in fiat currency is poor and is missing out on the ability to have a good life. The average person with $15 in cryptocurrency is a dabbler who opened up a wallet once for fun. Inequality in level of interest is a healthy thing; every community has its dabblers and its full-time hardcore fans with no life. So if a cryptocurrency has a very high Gini coefficient, but it turns out that much of this inequality comes from inequality in level of interest, then the number points to a much less scary reality than the headlines imply.Cryptocurrencies, even those that turn out to be highly plutocratic, will not turn any part of the world into anything close to dystopia A. But badly-distributed cryptocurrencies may well look like dystopia B, a problem compounded if coin voting governance is used to make protocol decisions. Hence, to detect the problems that cryptocurrency communities worry about most, we want a metric that captures proximity to dystopia B more specifically.An alternative: measuring dystopia A problems and dystopia B problems separatelyAn alternative approach to measuring inequality involves directly estimating suffering from resources being unequally distributed (that is, "dystopia A" problems). First, start with some utility function representing the value of having a certain amount of money. \(log(x)\) is popular, because it captures the intuitively appealing approximation that doubling one's income is about as useful at any level: going from $10,000 to $20,000 adds the same utility as going from $5,000 to $10,000 or from $40,000 to $80,000). The score is then a matter of measuring how much utility is lost compared to if everyone just got the average income:\(log(\frac^n x_i}) - \frac^n log(x_i)}\)The first term (log-of-average) is the utility that everyone would have if money were perfectly redistributed, so everyone earned the average income. The second term (average-of-log) is the average utility in that economy today. The difference represents lost utility from inequality, if you look narrowly at resources as something used for personal consumption. There are other ways to define this formula, but they end up being close to equivalent (eg. the 1969 paper by Anthony Atkinson suggested an "equally distributed equivalent level of income" metric which, in the \(U(x) = log(x)\) case, is just a monotonic function of the above, and the Theil L index is perfectly mathematically equivalent to the above formula).To measure concentration (or "dystopia B" problems), the Herfindahl-Hirschman index is an excellent place to start, and is already used to measure economic concentration in industries:\(\frac^n x_i^2}^n x_i)^2}\)Or for you visual learners out there: Herfindahl-Hirschman index: green area divided by total area.There are other alternatives to this; the Theil T index has some similar properties though also some differences. A simpler-and-dumber alternative is the Nakamoto coefficient: the minimum number of participants needed to add up to more than 50% of the total. Note that all three of these concentration indices focus heavily on what happens near the top (and deliberately so): a large number of dabblers with a small quantity of resources contributes little or nothing to the index, while the act of two top participants merging can make a very big change to the index.For cryptocurrency communities, where concentration of resources is one of the biggest risks to the system but where someone only having 0.00013 coins is not any kind of evidence that they're actually starving, adopting indices like this is the obvious approach. But even for countries, it's probably worth talking about, and measuring, concentration of power and suffering from lack of resources more separately.That said, at some point we have to move beyond even these indices. The harms from concentration are not just a function of the size of the actors; they are also heavily dependent on the relationships between the actors and their ability to collude with each other. Similarly, resource allocation is network-dependent: lack of formal resources may not be that harmful if the person lacking resources has an informal network to tap into. But dealing with these issues is a much harder challenge, and so we do also need the simpler tools while we still have less data to work with.

Verkle trees Verkle trees2021 Jun 18 See all posts Verkle trees Special thanks to Dankrad Feist and Justin Drake for feedback and review.Verkle trees are shaping up to be an important part of Ethereum's upcoming scaling upgrades. They serve the same function as Merkle trees: you can put a large amount of data into a Verkle tree, and make a short proof ("witness") of any single piece, or set of pieces, of that data that can be verified by someone who only has the root of the tree. The key property that Verkle trees provide, however, is that they are much more efficient in proof size. If a tree contains a billion pieces of data, making a proof in a traditional binary Merkle tree would require about 1 kilobyte, but in a Verkle tree the proof would be less than 150 bytes - a reduction sufficient to make stateless clients finally viable in practice.Verkle trees are still a new idea; they were first introduced by John Kuszmaul in this paper from 2018, and they are still not as widely known as many other important new cryptographic constructions. This post will explain what Verkle trees are and how the cryptographic magic behind them works. The price of their short proof size is a higher level of dependence on more complicated cryptography. That said, the cryptography still much simpler, in my opinion, than the advanced cryptography found in modern ZK SNARK schemes. In this post I'll do the best job that I can at explaining it.Merkle Patricia vs Verkle Tree node structureIn terms of the structure of the tree (how the nodes in the tree are arranged and what they contain), a Verkle tree is very similar to the Merkle Patricia tree currently used in Ethereum. Every node is either (i) empty, (ii) a leaf node containing a key and value, or (iii) an intermediate node that has some fixed number of children (the "width" of the tree). The value of an intermediate node is computed as a hash of the values of its children.The location of a value in the tree is based on its key: in the diagram below, to get to the node with key 4cc, you start at the root, then go down to the child at position 4, then go down to the child at position c (remember: c = 12 in hexadecimal), and then go down again to the child at position c. To get to the node with key baaa, you go to the position-b child of the root, and then the position-a child of that node. The node at path (b,a) directly contains the node with key baaa, because there are no other keys in the tree starting with ba.The structure of nodes in a hexary (16 children per parent) Verkle tree, here filled with six (key, value) pairs.The only real difference in the structure of Verkle trees and Merkle Patricia trees is that Verkle trees are wider in practice. Much wider. Patricia trees are at their most efficient when width = 2 (so Ethereum's hexary Patricia tree is actually quite suboptimal). Verkle trees, on the other hand, get shorter and shorter proofs the higher the width; the only limit is that if width gets too high, proofs start to take too long to create. The Verkle tree proposed for Ethereum has a width of 256, and some even favor raising it to 1024 (!!).Commitments and proofsIn a Merkle tree (including Merkle Patricia trees), the proof of a value consists of the entire set of sister nodes: the proof must contain all nodes in the tree that share a parent with any of the nodes in the path going down to the node you are trying to prove. That may be a little complicated to understand, so here's a picture of a proof for the value in the 4ce position. Sister nodes that must be included in the proof are highlighted in red.That's a lot of nodes! You need to provide the sister nodes at each level, because you need the entire set of children of a node to compute the value of that node, and you need to keep doing this until you get to the root. You might think that this is not that bad because most of the nodes are zeroes, but that's only because this tree has very few nodes. If this tree had 256 randomly-allocated nodes, the top layer would almost certainly have all 16 nodes full, and the second layer would on average be ~63.3% full.In a Verkle tree, on the other hand, you do not need to provide sister nodes; instead, you just provide the path, with a little bit extra as a proof. This is why Verkle trees benefit from greater width and Merkle Patricia trees do not: a tree with greater width leads to shorter paths in both cases, but in a Merkle Patricia tree this effect is overwhelmed by the higher cost of needing to provide all the width - 1 sister nodes per level in a proof. In a Verkle tree, that cost does not exist.So what is this little extra that we need as a proof? To understand that, we first need to circle back to one key detail: the hash function used to compute an inner node from its children is not a regular hash. Instead, it's a vector commitment.A vector commitment scheme is a special type of hash function, hashing a list \(h(z_1, z_2 ... z_n) \rightarrow C\). But vector commitments have the special property that for a commitment \(C\) and a value \(z_i\), it's possible to make a short proof that \(C\) is the commitment to some list where the value at the i'th position is \(z_i\). In a Verkle proof, this short proof replaces the function of the sister nodes in a Merkle Patricia proof, giving the verifier confidence that a child node really is the child at the given position of its parent node.No sister nodes required in a proof of a value in the tree; just the path itself plus a few short proofs to link each commitment in the path to the next.In practice, we use a primitive even more powerful than a vector commitment, called a polynomial commitment. Polynomial commitments let you hash a polynomial, and make a proof for the evaluation of the hashed polynomial at any point. You can use polynomial commitments as vector commitments: if we agree on a set of standardized coordinates \((c_1, c_2 ... c_n)\), given a list \((y_1, y_2 ... y_n)\) you can commit to the polynomial \(P\) where \(P(c_i) = y_i\) for all \(i \in [1..n]\) (you can find this polynomial with Lagrange interpolation). I talk about polynomial commitments at length in my article on ZK-SNARKs. The two polynomial commitment schemes that are the easiest to use are KZG commitments and bulletproof-style commitments (in both cases, a commitment is a single 32-48 byte elliptic curve point). Polynomial commitments give us more flexibility that lets us improve efficiency, and it just so happens that the simplest and most efficient vector commitments available are the polynomial commitments.This scheme is already very powerful as it is: if you use a KZG commitment and proof, the proof size is 96 bytes per intermediate node, nearly 3x more space-efficient than a simple Merkle proof if we set width = 256. However, it turns out that we can increase space-efficiency even further.Merging the proofsInstead of requiring one proof for each commitment along the path, by using the extra properties of polynomial commitments we can make a single fixed-size proof that proves all parent-child links between commitments along the paths for an unlimited number of keys. We do this using a scheme that implements multiproofs through random evaluation.But to use this scheme, we first need to convert the problem into a more structured one. We have a proof of one or more values in a Verkle tree. The main part of this proof consists of the intermediary nodes along the path to each node. For each node that we provide, we also have to prove that it actually is the child of the node above it (and in the correct position). In our single-value-proof example above, we needed proofs to prove:That the key: 4ce node actually is the position-e child of the prefix: 4c intermediate node. That the prefix: 4c intermediate node actually is the position-c child of the prefix: 4 intermediate node. That the prefix: 4 intermediate node actually is the position-4 child of the root If we had a proof proving multiple values (eg. both 4ce and 420), we would have even more nodes and even more linkages. But in any case, what we are proving is a sequence of statements of the form "node A actually is the position-i child of node B". If we are using polynomial commitments, this turns into equations: \(A(x_i) = y\), where \(y\) is the hash of the commitment to \(B\).The details of this proof are technical and better explained by Dankrad Feist than myself. By far the bulkiest and time-consuming step in the proof generation involves computing a polynomial \(g\) of the form:\(g(X) = r^0\frac + r^1\frac + ... + r^n\frac\)It is only possible to compute each term \(r^i\frac\) if that expression is a polynomial (and not a fraction). And that requires \(A_i(X)\) to equal \(y_i\) at the point \(x_i\).We can see this with an example. Suppose:\(A_i(X) = X^2 + X + 3\) We are proving for \((x_i = 2, y_i = 9)\). \(A_i(2)\) does equal \(9\) so this will work. \(A_i(X) - 9 = X^2 + X - 6\), and \(\frac\) gives a clean \(X - 3\). But if we tried to fit in \((x_i = 2, y_i = 10)\), this would not work; \(X^2 + X - 7\) cannot be cleanly divided by \(X - 2\) without a fractional remainder.The rest of the proof involves providing a polynomial commitment to \(g(X)\) and then proving that the commitment is actually correct. Once again, see Dankrad's more technical description for the rest of the proof.One single proof proves an unlimited number of parent-child relationships.And there we have it, that's what a maximally efficient Verkle proof looks like.Key properties of proof sizes using this schemeDankrad's multi-random-evaluation proof allows the prover to prove an arbitrary number of evaluations \(A_i(x_i) = y_i\), given commitments to each \(A_i\) and the values that are being proven. This proof is constant size (one polynomial commitment, one number, and two proofs; 128-1000 bytes depending on what scheme is being used). The \(y_i\) values do not need to be provided explicitly, as they can be directly computed from the other values in the Verkle proof: each \(y_i\) is itself the hash of the next value in the path (either a commitment or a leaf). The \(x_i\) values also do not need to be provided explicitly, since the paths (and hence the \(x_i\) values) can be computed from the keys and the coordinates derived from the paths. Hence, all we need is the leaves (keys and values) that we are proving, as well as the commitments along the path from each leaf to the root. Assuming a width-256 tree, and \(2^\) nodes, a proof would require the keys and values that are being proven, plus (on average) three commitments for each value along the path from that value to the root. If we are proving many values, there are further savings: no matter how many values you are proving, you will not need to provide more than the 256 values at the top level. Proof sizes (bytes). Rows: tree size, cols: key/value pairs proven 1 10 100 1,000 10,000 256 176 176 176 176 176 65,536 224 608 4,112 12,176 12,464 16,777,216 272 1,040 8,864 59,792 457,616 4,294,967,296 320 1,472 13,616 107,744 937,472 Assuming width 256, and 48-byte KZG commitments/proofs. Note also that this assumes a maximally even tree; for a realistic randomized tree, add a depth of ~0.6 (so ~30 bytes per element). If bulletproof-style commitments are used instead of KZG, it's safe to go down to 32 bytes, so these sizes can be reduced by 1/3.Prover and verifier computation loadThe bulk of the cost of generating a proof is computing each \(r^i\frac\) expression. This requires roughly four field operations (ie. 256 bit modular arithmetic operations) times the width of the tree. This is the main constraint limiting Verkle tree widths. Fortunately, four field operations is a small cost: a single elliptic curve multiplication typically takes hundreds of field operations. Hence, Verkle tree widths can go quite high; width 256-1024 seems like an optimal range.To edit the tree, we need to "walk up the tree" from the leaf to the root, changing the intermediate commitment at each step to reflect the change that happened lower down. Fortunately, we don't have to re-compute each commitment from scratch. Instead, we take advantage of the homomorphic property: given a polynomial commitment \(C = com(F)\), we can compute \(C' = com(F + G)\) by taking \(C' = C + com(G)\). In our case, \(G = L_i * (v_ - v_)\), where \(L_i\) is a pre-computed commitment for the polynomial that equals 1 at the position we're trying to change and 0 everywhere else.Hence, a single edit requires ~4 elliptic curve multiplications (one per commitment between the leaf and the root, this time including the root), though these can be sped up considerably by pre-computing and storing many multiples of each \(L_i\).Proof verification is quite efficient. For a proof of N values, the verifier needs to do the following steps, all of which can be done within a hundred milliseconds for even thousands of values:One size-\(N\) elliptic curve fast linear combination About \(4N\) field operations (ie. 256 bit modular arithmetic operations) A small constant amount of work that does not depend on the size of the proof Note also that, like Merkle Patricia proofs, a Verkle proof gives the verifier enough information to modify the values in the tree that are being proven and compute the new root hash after the changes are applied. This is critical for verifying that eg. state changes in a block were processed correctly.ConclusionsVerkle trees are a powerful upgrade to Merkle proofs that allow for much smaller proof sizes. Instead of needing to provide all "sister nodes" at each level, the prover need only provide a single proof that proves all parent-child relationships between all commitments along the paths from each leaf node to the root. This allows proof sizes to decrease by a factor of ~6-8 compared to ideal Merkle trees, and by a factor of over 20-30 compared to the hexary Patricia trees that Ethereum uses today (!!).They do require more complex cryptography to implement, but they present the opportunity for large gains to scalability. In the medium term, SNARKs can improve things further: we can either SNARK the already-efficient Verkle proof verifier to reduce witness size to near-zero, or switch back to SNARKed Merkle proofs if/when SNARKs get much better (eg. through GKR, or very-SNARK-friendly hash functions, or ASICs). Further down the line, the rise of quantum computing will force a change to STARKed Merkle proofs with hashes as it makes the linear homomorphisms that Verkle trees depend on insecure. But for now, they give us the same scaling gains that we would get with such more advanced technologies, and we already have all the tools that we need to implement them efficiently.

Blockchain voting is overrated among uninformed people but underrated among informed people Blockchain voting is overrated among uninformed people but underrated among informed people2021 May 25 See all posts Blockchain voting is overrated among uninformed people but underrated among informed people Special thanks to Karl Floersch, Albert Ni, Mr Silly and others for feedback and discussionVoting is a procedure that has a very important need for process integrity. The result of the vote must be correct, and this must be guaranteed by a transparent process so that everyone can be convinced that the result is correct. It should not be possible to successfully interfere with anyone's attempt to vote or prevent their vote from being counted.Blockchains are a technology which is all about providing guarantees about process integrity. If a process is run on a blockchain, the process is guaranteed to run according to some pre-agreed code and provide the correct output. No one can prevent the execution, no one can tamper with the execution, and no one can censor and block any users' inputs from being processed.So at first glance, it seems that blockchains provide exactly what voting needs. And I'm far from the only person to have had that thought; plenty of major prospective users are interested. But as it turns out, some people have a very different opinion.... Despite the seeming perfect match between the needs of voting and the technological benefits that blockchains provide, we regularly see scary articles arguing against the combination of the two. And it's not just a single article: here's an anti-blockchain-voting piece from Scientific American, here's another from CNet, and here's another from ArsTechnica. And it's not just random tech journalists: Bruce Schneier is against blockchain voting, and researchers at MIT wrote a whole paper arguing that it's a bad idea. So what's going on?OutlineThere are two key lines of criticism that are most commonly levied by critics of blockchain voting protocols:Blockchains are the wrong software tool to run an election. The trust properties they provide are not a good match for the properties that voting needs, and other kinds of software tools with different information flow and trust properties would work better. Software in general cannot be trusted to run elections, no matter what software it is. The risk of undetectable software and hardware bugs is too high, no matter how the platform is organized. This article will discuss both of these claims in turn ("refute" is too strong a word, but I definitely disagree more than I agree with both claims). First, I will discuss the security issues with existing attempts to use blockchains for voting, and how the correct solution is not to abandon blockchains, but to combine them with other cryptographic technologies. Second, I will address the concern about whether or not software (and hardware) can be trusted. The answer: computer security is actually getting quite a bit better, and we can work hard to continue that trend.Over the long term, insisting on paper permanently would be a huge handicap to our ability to make voting better. One vote per N years is a 250-year-old form of democracy, and we can have much better democracy if voting were much more convenient and simpler, so that we could do it much more often.Needless to say, this entire post is predicated on good blockchain scaling technology (eg. sharding) being available. Of course, if blockchains cannot scale, none of this can happen. But so far, development of this technology is proceeding quickly, and there's no reason to believe that it can't happen.Bad blockchain voting protocolsBlockchain voting protocols get hacked all the time. Two years ago, a blockchain voting tech company called Voatz was all the rage, and many people were very excited about it. But last year, some MIT researchers discovered a string of critical security vulnerabilities in their platform. Meanwhile, in Moscow, a blockchain voting system that was going to be used for an upcoming election was hacked, fortunately a month before the election took place.The hacks were pretty serious. Here is a table of the attack capabilities that researchers analyzing Voatz managed to uncover:This by itself is not an argument against ever using blockchain voting. But it is an argument that blockchain voting software should be designed more carefully, and scaled up slowly and incrementally over time.Privacy and coercion resistanceBut even the blockchain voting protocols that are not technically broken often suck. To understand why, we need to delve deeper into what specific security properties blockchains provide, and what specific security properties voting needs - when we do, we'll see that there is a mismatch.Blockchains provide two key properties: correct execution and censorship resistance. Correct execution just means that the blockchain accepts inputs ("transactions") from users, correctly processes them according to some pre-defined rules, and returns the correct output (or adjusts the blockchain's "state" in the correct way). Censorship resistance is also simple to understand: any user that wants to send a transaction, and is willing to pay a high enough fee, can send the transaction and expect to see it quickly included on-chain.Both of these properties are very important for voting: you want the output of the vote to actually be the result of counting up the number of votes for each candidate and selecting the candidate with the most votes, and you definitely want anyone who is eligible to vote to be able to vote, even if some powerful actor is trying to block them. But voting also requires some crucial properties that blockchains do not provide:Privacy: you should not be able to tell which candidate someone specific voted for, or even if they voted at all Coercion resistance: you should not be able to prove to someone else how you voted, even if you want to The need for the first requirement is obvious: you want people to vote based on their personal feelings, and not how people around them or their employer or the police or random thugs on the street will feel about their choice. The second requirement is needed to prevent vote selling: if you can prove how you voted, selling your vote becomes very easy. Provability of votes would also enable forms of coercion where the coercer demands to see some kind of proof of voting for their preferred candidate. Most people, even those aware of the first requirement, do not think about the second requirement. But the second requirement is also necessary, and it's quite technically nontrivial to provide it. Needless to say, the average "blockchain voting system" that you see in the wild does not even try to provide the second property, and usually fails at providing the first.Secure electronic voting without blockchainsThe concept of cryptographically secured execution of social mechanisms was not invented by blockchain geeks, and indeed existed far before us. Outside the blockchain space, there is a 20-year-old tradition of cryptographers working on the secure electronic voting problem, and the good news is that there have been solutions. An important paper that is cited by much of the literature of the last two decades is Juels, Catalano and Jakobsson's 2002 paper titled "Coercion-Resistant Electronic Elections":Since then, there have been many iterations on the concept; Civitas is one prominent example, though there are also many others. These protocols all use a similar set of core techniques. There is an agreed-upon set of "talliers" and there is a trust assumption that the majority of the talliers is honest. The talliers each have "shares" of a private key secret-shared among themselves, and the corresponding public key is published. Voters publish votes encrypted to the talliers' public key, and talliers use a secure multi-party computation (MPC) protocol to decrypt and verify the votes and compute the tally. The tallying computation is done "inside the MPC": the talliers never learn their private key, and they compute the final result without learning anything about any individual vote beyond what can be learned from looking at the final result itself.Encrypting votes provides privacy, and some additional infrastructure such as mix-nets is added on top to make the privacy stronger. To provide coercion resistance, one of two techniques is used. One option is that during the registration phase (the phase in which the talliers learn each registered voter's public key), the voter generates or receives a secret key. The corresponding public key is secret shared among the talliers, and the talliers' MPC only counts a vote if it is signed with the secret key. A voter has no way to prove to a third party what their secret key is, so if they are bribed or coerced they can simply show and cast a vote signed with the wrong secret key. Alternatively, a voter could have the ability to send a message to change their secret key. A voter has no way of proving to a third party that they did not send such a message, leading to the same result.The second option is a technique where voters can make multiple votes where the second overrides the first. If a voter is bribed or coerced, they can make a vote for the briber/coercer's preferred candidate, but later send another vote to override the first.Giving voters the ability to make a later vote that can override an earlier vote is the key coercion-resistance mechanism of this protocol from 2015.Now, we get to a key important nuance in all of these protocols. They all rely on an outside primitive to complete their security guarantees: the bulletin board (this is the "BB" in the figure above). The bulletin board is a place where any voter can send a message, with a guarantee that (i) anyone can read the bulletin board, and (ii) anyone can send a message to the bulletin board that gets accepted. Most of the coercion-resistant voting papers that you can find will casually reference the existence of a bulletin board (eg. "as is common for electronic voting schemes, we assume a publicly accessible append-only bulletin board"), but far fewer papers talk about how this bulletin board can actually be implemented. And here, you can hopefully see where I am going with this: the most secure way to implement a bulletin board is to just use an existing blockchain!Secure electronic voting with blockchainsOf course, there have been plenty of pre-blockchain attempts at making a bulletin board. This paper from 2008 is such an attempt; its trust model is a standard requirement that "k of n servers must be honest" (k = n/2 is common). This literature review from 2021 covers some pre-blockchain attempts at bulletin boards as well as exploring the use of blockchains for the job; the pre-blockchain solutions reviewed similarly rely on a k-of-n trust model.A blockchain is also a k-of-n trust model; it requires at least half of miners or proof of stake validators to be following the protocol, and if that assumption fails that often results in a "51% attack". So why is a blockchain better than a special purpose bulletin board? The answer is: setting up a k-of-n system that's actually trusted is hard, and blockchains are the only system that has already solved it, and at scale. Suppose that some government announced that it was making a voting system, and provided a list of 15 local organizations and universities that would be running a special-purpose bulletin board. How would you, as an outside observer, know that the government didn't just choose those 15 organizations from a list of 1000 based on their willingness to secretly collude with an intelligence agency?Public blockchains, on the other hand, have permissionless economic consensus mechanisms (proof of work or proof of stake) that anyone can participate in, and they have an existing diverse and highly incentivized infrastructure of block explorers, exchanges and other watching nodes to constantly verify in real time that nothing bad is going on.These more sophisticated voting systems are not just using blockchains; they rely on cryptography such as zero knowledge proofs to guarantee correctness, and on multi-party computation to guarantee coercion resistance. Hence, they avoid the weaknesses of more naive systems that simply just "put votes directly on the blockchain" and ignore the resulting privacy and coercion resistance issues. However, the blockchain bulletin board is nevertheless a key part of the security model of the whole design: if the committee is broken but the blockchain is not, coercion resistance is lost but all the other guarantees around the voting process still remain.MACI: coercion-resistant blockchain voting in EthereumThe Ethereum ecosystem is currently experimenting with a system called MACI that combines together a blockchain, ZK-SNARKs and a single central actor that guarantees coercion resistance (but has no power to compromise any properties other than coercion resistance). MACI is not very technically difficult. Users participate by signing a message with their private key, encrypting the signed message to a public key published by a central server, and publishing the encrypted signed message to the blockchain. The server downloads the messages from the blockchain, decrypts them, processes them, and outputs the result along with a ZK-SNARK to ensure that they did the computation correctly. Users cannot prove how they participated, because they have the ability to send a "key change" message to trick anyone trying to audit them: they can first send a key change message to change their key from A to B, and then send a "fake message" signed with A. The server would reject the message, but no one else would have any way of knowing that the key change message had ever been sent. There is a trust requirement on the server, though only for privacy and coercion resistance; the server cannot publish an incorrect result either by computing incorrectly or by censoring messages. In the long term, multi-party computation can be used to decentralize the server somewhat, strengthening the privacy and coercion resistance guarantees.There is a working demo of this scheme at clr.fund being used for quadratic funding. The use of the Ethereum blockchain to ensure censorship resistance of votes ensures a much higher degree of censorship resistance than would be possible if a committee was relied on for this instead.RecapThe voting process has four important security requirements that must be met for a vote to be secure: correctness, censorship resistance, privacy and coercion resistance. Blockchains are good at the first two. They are bad at the last two. Encryption of votes put on a blockchain can add privacy. Zero knowledge proofs can bring back correctness despite observers being unable to add up votes directly because they are encrypted. Multi-party computation decrypting and checking votes can provide coercion resistance, if combined with a mechanic where users can interact with the system multiple times; either the first interaction invalidates the second, or vice versa Using a blockchain ensures that you have very high-security censorship resistance, and you keep this censorship resistance even if the committee colludes and breaks coercion resistance. Introducing a blockchain can significantly increase the level of security of the system. But can technology be trusted?But now we get back to the second, deeper, critique of electronic voting of any kind, blockchain or not: that technology itself is too insecure to be trusted.The recent MIT paper criticizing blockchain voting includes this helpful table, depicting any form of paperless voting as being fundamentally too difficult to secure: The key property that the authors focus on is software-independence, which they define as "the property that an undetected change or error in a system's software cannot cause an undetectable change in the election outcome". Basically, a bug in the code should not be able to accidentally make Prezzy McPresidentface the new president of the country (or, more realistically, a deliberately inserted bug should not be able to increase some candidate's share from 42% to 52%).But there are other ways to deal with bugs. For example, any blockchain-based voting system that uses publicly verifiable zero-knowledge proofs can be independently verified. Someone can write their own implementation of the proof verifier and verify the Zk-SNARK themselves. They could even write their own software to vote. Of course, the technical complexity of actually doing this is beyond 99.99% of any realistic voter base, but if thousands of independent experts have the ability to do this and verify that it works, that is more than good enough in practice.To the MIT authors, however, that is not enough:Thus, any system that is electronic only, even if end-to-end verifiable, seems unsuitable for political elections in the foreseeable future. The U.S. Vote Foundation has noted the promise of E2E-V methods for improving online voting security, but has issued a detailed report recommending avoiding their use for online voting unless and until the technology is far more mature and fully tested in pollsite voting [38].Others have proposed extensions of these ideas. For example, the proposal of Juels et al. [55] emphasizes the use of cryptography to provide a number of forms of "coercion resistance." The Civitas proposal of Clarkson et al. [24] implements additional mechanisms for coercion resistance, which Iovino et al. [53] further incorporate and elaborate into their Selene system. From our perspective, these proposals are innovative but unrealistic: they are quite complex, and most seriously, their security relies upon voters' devices being uncompromised and functioning as intended, an unrealistic assumption.The problem that the authors focus on is not the voting system's hardware being secure; risks on that side actually can be mitigated with zero knowledge proofs. Rather, the authors focus on a different security problem: can users' devices even in principle be made secure?Given the long history of all kinds of exploits and hacks of consumer devices, one would be very justified in thinking the answer is "no". Quoting my own article on Bitcoin wallet security from 2013:Last night around 9PM PDT, I clicked a link to go to CoinChat[.]freetzi[.]com – and I was prompted to run java. I did (thinking this was a legitimate chatoom), and nothing happened. I closed the window and thought nothing of it. I opened my bitcoin-qt wallet approx 14 minutes later, and saw a transaction that I did NOT approve go to wallet 1Es3QVvKN1qA2p6me7jLCVMZpQXVXWPNTC for almost my entire wallet...And:In June 2011, the Bitcointalk member "allinvain" lost 25,000 BTC (worth $500,000 at the time) after an unknown intruder somehow gained direct access to his computer. The attacker was able to access allinvain's wallet.dat file, and quickly empty out the wallet – either by sending a transaction from allinvain's computer itself, or by simply uploading the wallet.dat file and emptying it on his own machine.But these disasters obscure a greater truth: over the past twenty years, computer security has actually been slowly and steadily improving. Attacks are much harder to find, often requiring the attacker to find bugs in multiple sub-systems instead of finding a single hole in a large complex piece of code. High-profile incidents are larger than ever, but this is not a sign that anything is getting less secure; rather, it's simply a sign that we are becoming much more dependent on the internet.Trusted hardware is a very important recent source of improvements. Some of the new "blockchain phones" (eg. this one from HTC) go quite far with this technology and put a minimalistic security-focused operating system on the trusted hardware chip, allowing high-security-demanding applications (eg. cryptocurrency wallets) to stay separate from the other applications. Samsung has started making phones using similar technology. And even devices that are never advertised as "blockchain devices" (eg. iPhones) frequently have trusted hardware of some kind. Cryptocurrency hardware wallets are effectively the same thing, except the trusted hardware module is physically located outside the computer instead of inside it. Trusted hardware (deservedly!) often gets a bad rap in security circles and especially the blockchain community, because it just keeps getting broken again and again. And indeed, you definitely don't want to use it to replace your security protection. But as an augmentation, it's a huge improvement.Finally, single applications, like cryptocurrency wallets and voting systems, are much simpler and have less room for error than an entire consumer operating system - even if you have to incorporate support for quadratic voting, sortition, quadratic sortition and whatever horrors the next generation's Glen Weyl invents in 2040. The benefit of tools like trusted hardware is their ability to isolate the simple thing from the complex and possibly broken thing, and these tools are having some success.So the risks might decrease over time. But what are the benefits?These improvements in security technology point to a future where consumer hardware might be more trusted in the future than it is today. Investments made in this area in the last few years are likely to keep paying off over the next decade, and we could expect further significant improvements. But what are the benefits of making voting electronic (blockchain based or otherwise) that justify exploring this whole space?My answer is simple: voting would become much more efficient, allowing us to do it much more often. Currently, formal democratic input into organizations (governmental or corporate) tends to be limited to a single vote once every 1-6 years. This effectively means that each voter is only putting less than one bit of input into the system each year. Perhaps in large part as a result of this, decentralized decision-making in our society is heavily bifurcated into two extremes: pure democracy and pure markets. Democracy is either very inefficient (corporate and government votes) or very insecure (social media likes/retweets). Markets are far more technologically efficient and are much more secure than social media, but their fundamental economic logic makes them a poor fit for many kinds of decision problems, particularly having to do with public goods.Yes, I know it's yet another triangle, and I really really apologize for having to use it. But please bear with me just this once.... (ok fine, I'm sure I'll make even more triangles in the future; just suck it up and deal with it)There is a lot that we could do if we could build more systems that are somewhere in between democracy and markets, benefiting from the egalitarianism of the former, the technical efficiency of the latter and economic properties all along the spectrum in between the two extremes. Quadratic funding is an excellent example of this. Liquid democracy is another excellent example. Even if we don't introduce fancy new delegation mechanisms or quadratic math, there's a lot that we could do by doing voting much more and at smaller scales more adapted to the information available to each individual voter. But the challenge with all of these ideas is that in order to have a scheme that durably maintains any level of democraticness at all, you need some form of sybil resistance and vote-buying mitigation: exactly the problems that these fancy ZK-SNARK + MPC + blockchain voting schemes are trying to solve.The crypto space can helpOne of the underrated benefits of the crypto space is that it's an excellent "virtual special economic zone" for testing out economic and cryptographic ideas in a highly adversarial environment. Whatever you build and release, once the economic power that it controls gets above a certain size, a whole host of diverse, sometimes altruistic, sometimes profit-motivated, and sometimes malicious actors, many of whom are completely anonymous, will descend upon the system and try to twist that economic power toward their own various objectives.The incentives for attackers are high: if an attacker steals $100 from your cryptoeconomic gadget, they can often get the full $100 in reward, and they can often get away with it. But the incentives for defenders are also high: if you develop a tool that helps users not lose their funds, you could (at least sometimes) turn that into a tool and earn millions. Crypto is the ultimate training zone: if you can build something that can survive in this environment at scale, it can probably also survive in the bigger world as well.This applies to quadratic funding, it applies to multisig and social recovery wallets, and it can apply to voting systems too. The blockchain space has already helped to motivate the rise of important security technologies:Hardware wallets Efficient general-purpose zero knowledge proofs Formal verification tools "Blockchain phones" with trusted hardware chips Anti-sybil schemes like Proof of Humanity In all of these cases, some version of the technology existed before blockchains came onto the scene. But it's hard to deny that blockchains have had a significant impact in pushing these efforts forward, and the large role of incentives inherent to the space plays a key role in raising the stakes enough for the development of the tech to actually happen.ConclusionIn the short term, any form of blockchain voting should certainly remain confined to small experiments, whether in small trials for more mainstream applications or for the blockchain space itself. Security is at present definitely not good enough to rely on computers for everything. But it's improving, and if I am wrong and security fails to improve then not only blockchain voting, but also cryptocurrency as a whole, will have a hard time being successful. Hence, there is a large incentive for the technology to continue to improve.We should all continue watching the technology and the efforts being made everywhere to try and increase security, and slowly become more comfortable using technology in very important social processes. Technology is already key in our financial markets, and a crypto-ization of a large part of the economy (or even just replacing gold) will put an even greater portion of the economy into the hands of our cryptographic algorithms and the hardware that is running them. We should watch and support this process carefully, and over time take advantage of its benefits to bring our governance technologies into the 21st century.

The Limits to Blockchain Scalability The Limits to Blockchain Scalability2021 May 23 See all posts The Limits to Blockchain Scalability Special thanks to Felix Lange, Martin Swende, Marius van der Wijden and Mark Tyneway for feedback and review.Just how far can you push the scalability of a blockchain? Can you really, as Elon Musk wishes, "speed up block time 10X, increase block size 10X & drop fee 100X" without leading to extreme centralization and compromising the fundamental properties that make a blockchain what it is? If not, how far can you go? What if you change the consensus algorithm? Even more importantly, what if you change the technology to introduce features such as ZK-SNARKs or sharding? A sharded blockchain can theoretically just keep adding more shards; is there such a thing as adding too many?As it turns out, there are important and quite subtle technical factors that limit blockchain scaling, both with sharding and without. In many cases there are solutions, but even with the solutions there are limits. This post will go through what many of these issues are. Just increase the parameters, and all problems are solved. But at what cost?It's crucial for blockchain decentralization for regular users to be able to run a nodeAt 2:35 AM, you receive an emergency call from your partner on the opposite side of the world who helps run your mining pool (or it could be a staking pool). Since about 14 minutes ago, your partner tells you, your pool and a few others split off from the chain which still carries 79% of the network. According to your node, the majority chain's blocks are invalid. There's a balance error: the key block appeared to erroneously assign 4.5 million extra coins to an unknown address.An hour later, you're in a telegram chat with the other two small pools who were caught blindsided just as you were, as well as some block explorers and exchanges. You finally see someone paste a link to a tweet, containing a published message. "Announcing new on-chain sustainable protocol development fund", the tweet begins.By the morning, arguments on Twitter, and on the one community forum that was not censoring the discussion, discussions are everywhere. But by then a significant part of the 4.5 million coins had been converted on-chain to other assets, and billions of dollars of defi transactions had taken place. 79% of the consensus nodes, and all the major block explorers and endpoints for light wallets, were following this new chain. Perhaps the new dev fund will fund some development, or perhaps it will just all be embezzled by the leading pools and exchanges and their cronies. But regardless of how it turns out, the fund is for all intents and purposes a fait accompli, and regular users have no way to fight back. Movie coming soon. Maybe it can be funded by MolochDAO or something.Can this happen on your blockchain? The elites of your blockchain community, including pools, block explorers and hosted nodes, are probably quite well-coordinated; quite likely they're all in the same telegram channels and wechat groups. If they really want to organize a sudden change to the protocol rules to further their own interests, then they probably can. The Ethereum blockchain has fully resolved consensus failures in ten hours; if your blockchain has only one client implementation, and you only need to deploy a code change to a few dozen nodes, coordinating a change to client code can be done much faster. The only reliable way to make this kind of coordinated social attack not effective is through passive defense from the one constituency that actually is decentralized: the users.Imagine how the story would have played out if the users were running nodes that verify the chain (whether directly or through more advanced indirect techniques), and automatically reject blocks that break the protocol rules even if over 90% of the miners or stakers support those blocks. If every user ran a verifying node, then the attack would have quickly failed: a few mining pools and exchanges would have forked off and looked quite foolish in the process. But even if some users ran verifying nodes, the attack would not have led to a clean victory for the attacker; rather, it would have led to chaos, with different users seeing different views of the chain. At the very least, the ensuing market panic and likely persistent chain split would greatly reduce the attackers' profits. The thought of navigating such a protracted conflict would itself deter most attacks. Listen to Hasu on this one.If you have a community of 37 node runners and 80000 passive listeners that check signatures and block headers, the attacker wins. If you have a community where everyone runs a node, the attacker loses. We don't know what the exact threshold is at which herd immunity against coordinated attacks kicks in, but there is one thing that's absolutely clear: more nodes good, fewer nodes bad, and we definitely need more than a few dozen or few hundred.So, what are the limits to how much work we can require full nodes to do?To maximize the number of users who can run a node, we'll focus on regular consumer hardware. There are some increases to capacity that can be achieved by demanding some specialized hardware purchases that are easy to obtain (eg. from Amazon), but they actually don't increase scalability by that much.There are three key limitations to a full node's ability to process a large number of transactions:Computing power: what % of the CPU can we safely demand to run a node? Bandwidth: given the realities of current internet connections, how many bytes can a block contain? Storage: how many gigabytes on disk can we require users to store? Also, how quickly must it be readable? (ie. is HDD okay or do we need SSD) Many erroneous takes on how far a blockchain can scale using "simple" techniques stem from overly optimistic estimates for each of these numbers. We can go through these three factors one by one:Computing powerBad answer: 100% of CPU power can be spent on block verification Correct answer: ~5-10% of CPU power can be spent on block verification There are four key reasons why the limit is so low:We need a safety margin to cover the possibility of DoS attacks (transactions crafted by an attacker to take advantage of weaknesses in code to take longer to process than regular transactions) Nodes need to be able to sync the chain after being offline. If I drop off the network for a minute, I should be able to catch up in a few seconds Running a node should not drain your battery very quickly and make all your other apps very slow There are other non-block-production tasks that nodes need to do as well, mostly around verifying and responding to incoming transactions and requests on the p2p network Note that up until recently, most explanations for "why only 5-10%?" focused on a different problem: that because PoW blocks come at random times, it taking a long time to verify blocks increases the risk that multiple blocks get created at the same time. There are many fixes to this problem (eg. Bitcoin NG, or just using proof of stake). But these fixes do NOT solve the other four problems, and so they don't enable large gains in scalability as many had initially thought.Parallelism is also not a magic bullet. Often, even clients of seemingly single-threaded blockchains are parallelized already: signatures can be verified by one thread while execution is done by other threads, and there's a separate thread that's handling transaction pool logic in the background. And the closer you get to 100% usage across all threads, the more energy-draining running a node becomes and the lower your safety margin against DoS.BandwidthBad answer: if we have 10 MB blocks every 2-3 seconds, then most users have a >10 MB/sec network, so of course they can handle it Correct answer: maybe we can handle 1-5 MB blocks every 12 seconds. It's hard though. Nowadays we frequently hear very high advertised statistics for how much bandwidth internet connections can offer: numbers of 100 Mbps and even 1 Gbps are common to hear. However, there is a large difference between advertised bandwidth and the expected actual bandwidth of a connection for several reasons:"Mbps" refers to "millions of bits per second"; a bit is 1/8 of a byte, so you need to divide advertised bit numbers by 8 to get the advertised byte numbers. Internet providers, just like all companies, often lie. There's always multiple applications using the same internet connection, so a node can't hog the entire bandwidth. p2p networks inevitably introduce their own overhead: nodes often end up downloading and re-uploading the same block multiple times (not to mention transactions being broadcasted through the mempool before being included in a block). When Starkware did an experiment in 2019 where they published 500 kB blocks after the transaction data gas cost decrease made that possible for the first time, a few nodes were actually unable to handle blocks of that size. Ability to handle large blocks has since been improved and will continue to be improved. But no matter what we do, we'll still be very far from being able to naively take the average bandwidth in MB/sec, convince ourselves that we're okay with 1s latency, and be able to have blocks that are that size.StorageBad answer: 10 terabytes Correct answer: 512 gigabytes The main argument here is, as you might guess, the same as elsewhere: the difference between theory and practice. In theory, there are 8 TB solid state drives that you can buy on Amazon (you do need SSDs or NVME; HDDs are too slow for storing the blockchain state). In practice, the laptop that was used to write this blog post has 512 GB, and if you make people go buy their own hardware, many of them will just get lazy (or they can't afford $800 for an 8 TB SSD) and use a centralized provider. And even if you can fit a blockchain onto some storage, a high level of activity can easily quickly burn through the disk and force you to keep getting a new one. A poll in a group of blockchain protocol researchers of how much disk space everyone has. Small sample size, I know, but still...Additionally, storage size determines the time needed for a new node to be able to come online and start participating in the network. Any data that existing nodes have to store is data that a new node has to download. This initial sync time (and bandwidth) is also a major barrier to users being able to run nodes. While writing this blog post, syncing a new geth node took me ~15 hours. If Ethereum had 10x more usage, syncing a new geth node would take at least a week, and it would be much more likely to just lead to your internet connection getting throttled. This is all even more important during an attack, when a successful response to the attack will likely involve many users spinning up new nodes when they were not running nodes before.Interaction effectsAdditionally, there are interaction effects between these three types of costs. Because databases use tree structures internally to store and retrieve data, the cost of fetching data from a database increases with the logarithm of the size of the database. In fact, because the top level (or top few levels) can be cached in RAM, the disk access cost is proportional to the size of the database as a multiple of the size of the data cached in RAM. Don't take this diagram too literally; different databases work in different ways, and often the part in memory is just a single (but big) layer (see LSM trees as used in leveldb). But the basic principles are the same.For example, if the cache is 4 GB, and we assume that each layer of the database is 4x bigger than the previous, then Ethereum's current ~64 GB state would require ~2 accesses. But if the state size increases by 4x to ~256 GB, then this would increase to ~3 accesses (so 1.5x more accesses per read). Hence, a 4x increase in the gas limit, which would increase both the state size and the number of reads, could actually translate into a ~6x increase in block verification time. The effect may be even stronger: hard disks often take longer to read and write when they are full than when they are near-empty.So what does this mean for Ethereum?Today in the Ethereum blockchain, running a node already is challenging for many users, though it is still at least possible on regular hardware (I just synced a node on my laptop while writing this post!). Hence, we are close to hitting bottlenecks. The issue that core developers are most concerned with is storage size. Thus, at present, valiant efforts at solving bottlenecks in computation and data, and even changes to the consensus algorithm, are unlikely to lead to large gas limit increases being accepted. Even solving Ethereum's largest outstanding DoS vulnerability only led to a gas limit increase of 20%.The only solution to storage size problems is statelessness and state expiry. Statelessness allows for a class of nodes that verify the chain without maintaining permanent storage. State expiry pushes out state that has not been recently accessed, forcing users to manually provide proofs to renew it. Both of these paths have been worked at for a long time, and proof-of-concept implementation on statelessness has already started. These two improvements combined can greatly alleviate these concerns and open up room for a significant gas limit increase. But even after statelessness and state expiry are implemented, gas limits may only increase safely by perhaps ~3x until the other limitations start to dominate.Another possible medium-term solution is using ZK-SNARKs to verify transactions. ZK-SNARKs would ensure that regular users do not have to personally store the state or verify blocks, though they still would need to download all the data in blocks to protect against data unavailability attacks. Additionally, even if attackers cannot force invalid blocks through, if capacity is increased to the point where running a consensus node is too difficult, there is still the risk of coordinated censorship attacks. Hence, ZK-SNARKs cannot increase capacity infinitely, but they still can increase capacity by a significant margin (perhaps 1-2 orders of magnitude). Some chains are exploring this approach at layer 1; Ethereum is getting the benefits of this approach through layer-2 protocols (called ZK rollups) such as zksync, Loopring and Starknet.What happens after sharding?Sharding fundamentally gets around the above limitations, because it decouples the data contained on a blockchain from the data that a single node needs to process and store. Instead of nodes verifying blocks by personally downloading and executing them, they use advanced mathematical and cryptographic techniques to verify blocks indirectly.As a result, sharded blockchains can safely have very high levels of transaction throughput that non-sharded blockchains cannot. This does require a lot of cryptographic cleverness in creating efficient substitutes for naive full validation that successfully reject invalid blocks, but it can be done: the theory is well-established and proof-of-concepts based on draft specifications are already being worked on. Ethereum is planning to use quadratic sharding, where total scalability is limited by the fact that a node has to be able to process both a single shard and the beacon chain which has to perform some fixed amount of management work for each shard. If shards are too big, nodes can no longer process individual shards, and if there are too many shards, nodes can no longer process the beacon chain. The product of these two constraints forms the upper bound.Conceivably, one could go further by doing cubic sharding, or even exponential sharding. Data availability sampling would certainly become much more complex in such a design, but it can be done. But Ethereum is not going further than quadratic. The reason is that the extra scalability gains that you get by going from shards-of-transactions to shards-of-shards-of-transactions actually cannot be realized without other risks becoming unacceptably high.So what are these risks?Minimum user countA non-sharded blockchain can conceivably run as long as there is even one user that cares to participate in it. Sharded blockchains are not like this: no single node can process the whole chain, and so you need enough nodes so that they can at least process the chain together. If each node can process 50 TPS, and the chain can process 10000 TPS, then the chain needs at least 200 nodes to survive. If the chain at any point gets to less than 200 nodes, then either nodes stop being able to keep up with the chain, or nodes stop being able to detect invalid blocks, or a number of other bad things may happen, depending on how the node software is set up.In practice, the safe minimum count is several times higher than the naive "chain TPS divided by node TPS" heuristic due to the need for redundancy (including for data availability sampling); for our above example, let's call it 1000 nodes.If a sharded blockchain's capacity increases by 10x, the minimum user count also increases by 10x. Now, you might ask: why don't we start with a little bit of capacity, and increase it only when we see lots of users so we actually need it, and decrease it if the user count goes back down?There are a few problems with this:A blockchain itself cannot reliably detect how many unique users are on it, and so this would require some kind of governance to detect and set the shard count. Governance over capacity limits can easily become a locus of division and conflict. What if many users suddenly and unexpectedly drop out at the same time? Increasing the minimum number of users needed for a fork to start makes it harder to defend against hostile takeovers. A minimum user count of under 1,000 is almost certainly fine. A minimum user count of 1 million, on the other hand, is certainly not. Even a minimum user count of 10,000 is arguably starting to get risky. Hence, it seems difficult to justify a sharded blockchain having more than a few hundred shards.History retrievabilityAn important property of a blockchain that users really value is permanence. A digital asset stored on a server will stop existing in 10 years when the company goes bankrupt or loses interest in maintaining that ecosystem. An NFT on Ethereum, on the other hand, is forever. Yes, people will still be downloading and examining your cryptokitties in the year 2371. Deal with it.But once a blockchain's capacity gets too high, it becomes harder to store all that data, until at some point there's a large risk that some part of history will just end up being stored by... nobody.Quantifying this risk is easy. Take the blockchain's data capacity in MB/sec, and multiply by ~30 to get the amount of data stored in terabytes per year. The current sharding plan has a data capacity of ~1.3 MB/sec, so about 40 TB/year. If that is increased by 10x, this becomes 400 TB/year. If we want the data to be not just accessible, but accessible conveniently, we would also need metadata (eg. decompressing rollup transactions), so make that 4 petabytes per year, or 40 petabytes after a decade. The Internet Archive uses 50 petabytes. So that's a reasonable upper bound for how large a sharded blockchain can safely get.Hence, it looks like on both of these dimensions, the Ethereum sharding design is actually already roughly targeted fairly close to reasonable maximum safe values. The constants can be increased a little bit, but not too much.SummaryThere are two ways to try to scale a blockchain: fundamental technical improvements, and simply increasing the parameters. Increasing the parameters sounds very attractive at first: if you do the math on a napkin, it is easy to convince yourself that a consumer laptop can process thousands of transactions per second, no ZK-SNARKs or rollups or sharding required. Unfortunately, there are many subtle reasons why this approach is fundamentally flawed.Computers running blockchain nodes cannot spend 100% of CPU power validating the chain; they need a large safety margin to resist unexpected DoS attacks, they need spare capacity for tasks like processing transactions in the mempool, and you don't want running a node on a computer to make that computer unusable for any other applications at the same time. Bandwidth similarly has overhead: a 10 MB/s connection does NOT mean you can have a 10 megabyte block every second! A 1-5 megabyte block every 12 seconds, maybe. And it is the same with storage. Increasing hardware requirements for running a node and limiting node-running to specialized actors is not a solution. For a blockchain to be decentralized, it's crucially important for regular users to be able to run a node, and to have a culture where running nodes is a common activity.Fundamental technical improvements, on the other hand, can work. Currently, the main bottleneck in Ethereum is storage size, and statelessness and state expiry can fix this and allow an increase of perhaps up to ~3x - but not more, as we want running a node to become easier than it is today. Sharded blockchains can scale much further, because no single node in a sharded blockchain needs to process every transaction. But even there, there are limits to capacity: as capacity goes up, the minimum safe user count goes up, and the cost of archiving the chain (and the risk that data is lost if no one bothers to archive the chain) goes up. But we don't have to worry too much: those limits are high enough that we can probably process over a million transactions per second with the full security of a blockchain. But it's going to take work to do this without sacrificing the decentralization that makes blockchains so valuable.

Why sharding is great: demystifying the technical properties Why sharding is great: demystifying the technical properties2021 Apr 07 See all posts Why sharding is great: demystifying the technical properties Special thanks to Dankrad Feist and Aditya Asgaonkar for reviewSharding is the future of Ethereum scalability, and it will be key to helping the ecosystem support many thousands of transactions per second and allowing large portions of the world to regularly use the platform at an affordable cost. However, it is also one of the more misunderstood concepts in the Ethereum ecosystem and in blockchain ecosystems more broadly. It refers to a very specific set of ideas with very specific properties, but it often gets conflated with techniques that have very different and often much weaker security properties. The purpose of this post will be to explain exactly what specific properties sharding provides, how it differs from other technologies that are not sharding, and what sacrifices a sharded system has to make to achieve these properties. One of the many depictions of a sharded version of Ethereum. Original diagram by Hsiao-wei Wang, design by Quantstamp.The Scalability TrilemmaThe best way to describe sharding starts from the problem statement that shaped and inspired the solution: the Scalability Trilemma. The scalability trilemma says that there are three properties that a blockchain try to have, and that, if you stick to "simple" techniques, you can only get two of those three. The three properties are:Scalability: the chain can process more transactions than a single regular node (think: a consumer laptop) can verify. Decentralization: the chain can run without any trust dependencies on a small group of large centralized actors. This is typically interpreted to mean that there should not be any trust (or even honest-majority assumption) of a set of nodes that you cannot join with just a consumer laptop. Security: the chain can resist a large percentage of participating nodes trying to attack it (ideally 50%; anything above 25% is fine, 5% is definitely not fine). Now we can look at the three classes of "easy solutions" that only get two of the three:Traditional blockchains - including Bitcoin, pre-PoS/sharding Ethereum, Litecoin, and other similar chains. These rely on every participant running a full node that verifies every transaction, and so they have decentralization and security, but not scalability. High-TPS chains - including the DPoS family but also many others. These rely on a small number of nodes (often 10-100) maintaining consensus among themselves, with users having to trust a majority of these nodes. This is scalable and secure (using the definitions above), but it is not decentralized. Multi-chain ecosystems - this refers to the general concept of "scaling out" by having different applications live on different chains and using cross-chain-communication protocols to talk between them. This is decentralized and scalable, but it is not secure, because an attacker need only get a consensus node majority in one of the many chains (so often

Gitcoin Grants Round 9: The Next Phase of Growth Gitcoin Grants Round 9: The Next Phase of Growth2021 Apr 02 See all posts Gitcoin Grants Round 9: The Next Phase of Growth Special thanks to the Gitcoin team for feedback and diagrams.Special note: Any criticism in these review posts of actions taken by people or organizations, especially using terms like "collusion", "bribe" and "cabal", is only in the spirit of analysis and mechanism design, and should not be taken as (especially moral) criticism of the people and organizations themselves. You're all well-intentioned and wonderful people and I love you.Gitcoin Grants Round 9 has just finished, and as usual the round has been a success. Along with 500,000 in matching funds, $1.38 million was donated by over 12,000 contributors to 812 different projects, making this the largest round so far. Not only old projects, but also new ones, received a large amount of funding, proving the mechanism's ability to avoid entrenchment and adapt to changing circumstances. The new East Asia-specific category in the latest two rounds has also been a success, helping to catapult multiple East Asian Ethereum projects to the forefront. However, with growing scale, round 9 has also brought out unique and unprecedented challenges. The most important among them is collusion and fraud: in round 9, over 15% of contributions were detected as being probably fraudulent. This was, of course, inevitable and expected from the start; I have actually been surprised at how long it has taken for people to start to make serious attempts to exploit the mechanism. The Gitcoin team has responded in force, and has published a blog post detailing their strategies for detecting and responding to adversarial behavior along with a general governance overview. However, it is my opinion that to successfully limit adversarial behavior in the long run more serious reforms, with serious sacrifices, are going to be required.Many new, and bigger, fundersGitcoin continues to be successful in attracting many matching funders this round. BadgerDAO, a project that describes itself as a "DAO dedicated to building products and infrastructure to bring Bitcoin to DeFi", has donated $300,000 to the matching pool - the largest single donation so far. Other new funders include Uniswap, Stakefish, Maskbook, FireEyes, Polygon, SushiSwap and TheGraph. As Gitcoin Grants continues to establish itself as a successful home for Ethereum public goods funding, it is also continuing to attract legitimacy as a focal point for donations from projects wishing to support the ecosystem. This is a sign of success, and hopefully it will continue and grow further. The next goal should be to get not just one-time contributions to the matching pool, but long-term commitments to repeated contributions (or even newly launched tokens donating a percentage of their holdings to the matching pool)!Churn continues to be healthyOne long-time concern with Gitcoin Grants is the balance between stability and entrenchment: if each project's match award changes too much from round to round, then it's hard for teams to rely on Gitcoin Grants for funding, and if the match awards change too little, it's hard for new projects to get included.We can measure this! To start off, let's compare the top-10 projects in this round to the top-10 projects in the previous round. In all cases, about half of the top-10 carries over from the previous round and about half is new (the flipside, of course is that half the top-10 drops out). The charts are a slight understatement: the Gitcoin Grants dev fund and POAP appear to have dropped out but actually merely changed categories, so something like 40% churn may be a more accurate number. If you check the results from round 8 against round 7, you also get about 50% churn, and comparing round 7 to round 6 gives similar values. Hence, it is looking like the degree of churn is stable. To me, it seems like roughly 40-50% churn is a healthy level, balancing long-time projects' need for stability with the need to avoid new projects getting locked out, but this is of course only my subjective judgement.Adversarial behaviorThe challenging new phenomenon this round was the sheer scale of the adversarial behavior that was attempted. In this round, there were two major issues. First, there were large clusters of contributors discovered that were probably a few individual or small closely coordinated groups with many accounts trying to cheat the mechanism. This was discovered by proprietary analysis algorithms used by the Gitcoin team.For this round, the Gitcoin team, in consultation with the community, decided to eat the cost of the fraud. Each project received the maximum of the match award it would receive if fraudulent transactions were accepted and the match award it would receive if they were not; the difference, about $33,000 in total, was paid out of Gitcoin's treasury. For future rounds, however, the team aims to be significantly stricter about security.A diagram from the Gitcoin team's post describin their process for finding and dealing with adversarial behavior.In the short term, simply ignoring fraud and accepting its costs has so far worked okay. In the long term, however, fraud must be dealt with, and this raises a challenging political concern. The algorithms that the Gitcoin team used to detect the adversarial behavior are proprietary and closed-source, and they have to be closed-source because otherwise the attackers could adapt and get around them. Hence, the output of the quadratic funding round is not just decided by a clear mathematical formula of the inputs. Rather, if fraudulent transactions were to be removed, it would also be fudged by what risks becoming a closed group twiddling with the outputs according to their arbitrary subjective judgements.It is worth stressing that this is not Gitcoin's fault. Rather, what is happening is that Gitcoin has gotten big enough that it has finally bumped into the exact same problem that every social media site, no matter how well-meaning its team, has been bumping into for the past twenty years. Reddit, despite its well-meaning and open-source-oriented team, employs many secretive tricks to detect and clamp down on vote manipulation, as does every other social media site.This is because making algorithms that prevent undesired manipulation, but continue to do so despite the attackers themselves knowing what these algorithms are, is really hard. In fact, the entire science of mechanism design is a half-century-long effort to try to solve this problem. Sometimes, there are successes. But often, they keep running into the same challenge: collusion. It turns out that it's not that hard to make mechanisms that give the outcomes you want if all of the participants are acting independently, but once you admit the possibility of one individual controlling many accounts, the problem quickly becomes much harder (or even intractable).But the fact that we can't achieve perfection doesn't mean that we can't try to come closer, and benefit from coming closer. Good mechanisms and opaque centralized intervention are substitutes: the better the mechanism, the closer to a good result the mechanism gets all by itself, and the more the secretive moderation cabal can go on vacation (an outcome that the actually-quite-friendly-and-cuddly and decentralization-loving Gitcoin moderation cabal very much wants!). In the short term, the Gitcoin team is also proactively taking a third approach: making fraud detection and response accountable by inviting third-party analysis and community oversight.Picture courtesy of the Gitcoin team's excellent blog post.Inviting community oversight is an excellent step in preserving the mechanism's legitimacy, and in paving the way for an eventual decentralization of the Gitcoin grants institution. However, it's not a 100% solution: as we've seen with technocratic organizations inside national governments, it's actually quite easy for them to retain a large amount of power despite formal democratic oversight and control. The long-term solution is shoring up Gitcoin's passive security, so that active security of this type becomes less necessary.One important form of passive security is making some form of unique-human verification no longer optional, but instead mandatory. Gitcoin already adds the option to use phone number verification, BrightID and several other techniques to "improve an account's trust score" and get greater matching. But what Gitcoin will likely be forced to do is make it so that some verification is required to get any matching at all. This will be a reduction in convenience, but the effects can be mitigated by the Gitcoin team's work on enabling more diverse and decentralized verification options, and the long-term benefit in enabling security without heavy reliance on centralized moderation, and hence getting longer-lasting legitimacy, is very much worth it.Retroactive airdropsA second major issue this round had to do with Maskbook. In February, Maskbook announced a token and the token distribution included a retroactive airdrop to anyone who had donated to Maskbook in previous rounds. The table from Maskbook's announcement post showing who is eligible for the airdrops.The controversy was that Maskbook was continuing to maintain a Gitcoin grant this round, despite now being wealthy and having set a precedent that donors to their grant might be rewarded in the future. The latter issue was particularly problematic as it could be construed as a form of obfuscated vote buying. Fortunately, the situation was defused quickly; it turned out that the Maskbook team had simply forgotten to consider shutting down the grant after they released their token, and they agreed to shut it down. They are now even part of the funders' league, helping to provide matching funds for future rounds!Another project attempted what some construed as a "wink wink nudge nudge" strategy of obfuscated vote buying: they hinted in chat rooms that they have a Gitcoin grant and they are going to have a token. No explicit promise to reward contributors was made, but there's a case that the people reading those messages could have interpreted it as such.In both cases, what we are seeing is that collusion is a spectrum, not a binary. In fact, there's a pretty wide part of the spectrum that even completely well-meaning and legitimate projects and their contributors could easily engage in. Note that this is a somewhat unusual "moral hierarchy". Normally, the more acceptable motivations would be the altruistic ones, and the less acceptable motivations would be the selfish ones. Here, though, the motivations closest to the left and the right are selfish; the altruistic motivation is close to the left, but it's not the only motivation close to the left. The key differentiator is something more subtle: are you contributing because you like the consequences of the project getting funded (inside-the-mechanism), or are you contributing because you like some (outside-the-mechanism) consequences of you personally funding the project?The latter motivation is problematic because it subverts the workings of quadratic funding. Quadratic funding is all about assuming that people contribute because they like the consequences of the project getting funded, recognizing that the amounts that people contribute will be much less than they ideally "should be" due to the tragedy of the commons, and mathematically compensating for that. But if there are large side-incentives for people to contribute, and these side-incentives are attached to that person specifically and so they are not reduced by the tragedy of the commons at all, then the quadratic matching magnifies those incentives into a very large distortion.In both cases (Maskbook, and the other project), we saw something in the middle. The case of the other project is clear: there was an accusation that they made hints at the possibility of formal compensation, though it was not explicitly promised. In the case of Maskbook, it seems as though Maskbook did nothing wrong: the airdrop was retroactive, and so none of the contributions to Maskbook were "tainted" with impute motives. But the problem is more long-term and subtle: if there's a long-term pattern of projects making retroactive airdrops to Gitcoin contributors, then users will feel a pressure to contribute primarily not to projects that they think are public goods, but rather to projects that they think are likely to later have tokens. This subverts the dream of using Gitcoin quadratic funding to provide alternatives to token issuance as a monetization strategy.The solution: making bribes (and retroactive airdrops) cryptographically impossibleThe simplest approach would be to delist projects whose behavior comes too close to collusion from Gitcoin. In this case, though, this solution cannot work: the problem is not projects doing airdrops while soliciting contributions, the problem is projects doing airdrops after soliciting contributions. While such a project is still soliciting contributions and hence vulnerable to being delisted, there is no indication that they are planning to do an airdrop. More generally, we can see from the examples above that policing motivations is a tough challenge with many gray areas, and is generally not a good fit for the spirit of mechanism design. But if delisting and policing motivations is not the solution, then what is?The solution comes in the form of a technology called MACI. MACI is a toolkit that allows you to run collusion-resistant applications, which simultaneously guarantee several key properties:Correctness: invalid messages do not get processed, and the result that the mechanism outputs actually is the result of processing all valid messages and correctly computing the result. Censorship resistance: if someone participates, the mechanism cannot cheat and pretend they did not participate by selectively ignoring their messages. Privacy: no one else can see how each individual participated. Collusion resistance: a participant cannot prove to others how they participated, even if they wanted to prove this. Collusion resistance is the key property: it makes bribes (or retroactive airdrops) impossible, because users would have no way to prove that they actually contributed to someone's grant or voted for someone or performed whatever other action. This is a realization of the secret ballot concept which makes vote buying impractical today, but with cryptography.The technical description of how this works is not that difficult. Users participate by signing a message with their private key, encrypting the signed message to a public key published by a central server, and publishing the encrypted signed message to the blockchain. The server downloads the messages from the blockchain, decrypts them, processes them, and outputs the result along with a ZK-SNARK to ensure that they did the computation correctly. Users cannot prove how they participated, because they have the ability to send a "key change" message to trick anyone trying to audit them: they can first send a key change message to change their key from A to B, and then send a "fake message" signed with A. The server would reject the message, but no one else would have any way of knowing that the key change message had ever been sent. There is a trust requirement on the server, though only for privacy and coercion resistance; the server cannot publish an incorrect result either by computing incorrectly or by censoring messages. In the long term, multi-party computation can be used to decentralize the server somewhat, strengthening the privacy and coercion resistance guarantees.There is already a quadratic funding system using MACI: clr.fund. It works, though at the moment proof generation is still quite expensive; ongoing work on the project will hopefully decrease these costs soon.Practical concernsNote that adopting MACI does come with necessary sacrifices. In particular, there would no longer be the ability to see who contributed to what, weakening Gitcoin's "social" aspects. However, the social aspects could be redesigned and changed by taking insights from elections: elections, despite their secret ballot, frequently give out "I voted" stickers. They are not "secure" (in that a non-voter can easily get one), but they still serve the social function. One could go further while still preserving the secret ballot property: one could make a quadratic funding setup where MACI outputs the value of how much each participant contributed, but not who they contributed to. This would make it impossible for specific projects to pay people to contribute to them, but would still leave lots of space for users to express their pride in contributing. Projects could airdrop to all Gitcoin contributors without discriminating by project, and announce that they're doing this together with a link to their Gitcoin profile. However, users would still be able to contribute to someone else and collect the airdrop; hence, this would arguably be within bounds of fair play.However, this is still a longer-term concern; MACI is likely not ready to be integrated for round 10. For the next few rounds, focusing on stepping up unique-human verification is still the best priority. Some ongoing reliance on centralized moderation will be required, though hopefully this can be simultaneously reduced and made more accountable to the community. The Gitcoin team has already been taking excellent steps in this direction. And if the Gitcoin team does successfully play their role as pioneers in being the first to brave and overcome these challenges, then we will end up with a secure and scalable quadratic funding system that is ready for much broader mainstream applications!

The Most Important Scarce Resource is Legitimacy The Most Important Scarce Resource is Legitimacy2021 Mar 23 See all posts The Most Important Scarce Resource is Legitimacy Special thanks to Karl Floersch, Aya Miyaguchi and Mr Silly for ideas, feedback and review.The Bitcoin and Ethereum blockchain ecosystems both spend far more on network security - the goal of proof of work mining - than they do on everything else combined. The Bitcoin blockchain has paid an average of about $38 million per day in block rewards to miners since the start of the year, plus about $5m/day in transaction fees. The Ethereum blockchain comes in second, at $19.5m/day in block rewards plus $18m/day in tx fees. Meanwhile, the Ethereum Foundation's annual budget, paying for research, protocol development, grants and all sorts of other expenses, is a mere $30 million per year. Non-EF-sourced funding exists too, but it is at most only a few times larger. Bitcoin ecosystem expenditures on R&D are likely even lower. Bitcoin ecosystem R&D is largely funded by companies (with $250m total raised so far according to this page), and this report suggests about 57 employees; assuming fairly high salaries and many paid developers not being counted, that works out to about $20m per year. Clearly, this expenditure pattern is a massive misallocation of resources. The last 20% of network hashpower provides vastly less value to the ecosystem than those same resources would if they had gone into research and core protocol development. So why not just.... cut the PoW budget by 20% and redirect the funds to those other things instead?The standard answer to this puzzle has to do with concepts like "public choice theory" and "Schelling fences": even though we could easily identify some valuable public goods to redirect some funding to as a one-off, making a regular institutionalized pattern of such decisions carries risks of political chaos and capture that are in the long run not worth it. But regardless of the reasons why, we are faced with this interesting fact that the organisms that are the Bitcoin and Ethereum ecosystems are capable of summoning up billions of dollars of capital, but have strange and hard-to-understand restrictions on where that capital can go.The powerful social force that is creating this effect is worth understanding. As we are going to see, it's also the same social force behind why the Ethereum ecosystem is capable of summoning up these resources in the first place (and the technologically near-identical Ethereum Classic is not). It's also a social force that is key to helping a chain recover from a 51% attack. And it's a social force that underlies all sorts of extremely powerful mechanisms far beyond the blockchain space. For reasons that will be clear in the upcoming sections, I will give this powerful social force a name: legitimacy.Coins can be owned by social contractsTo better understand the force that we are getting at, another important example is the epic saga of Steem and Hive. In early 2020, Justin Sun bought Steem-the-company, which is not the same thing as Steem-the-blockchain but did hold about 20% of the STEEM token supply. The community, naturally, did not trust Justin Sun. So they made an on-chain vote to formalize what they considered to be a longstanding "gentleman's agreement" that Steem-the-company's coins were held in trust for the common good of Steem-the-blockchain and should not be used to vote. With the help of coins held by exchanges, Justin Sun made a counterattack, and won control of enough delegates to unilaterally control the chain. The community saw no further in-protocol options. So instead they made a fork of Steem-the-blockchain, called Hive, and copied over all of the STEEM token balances - except those, including Justin Sun's, which participated in the attack.And they got plenty of applications on board. If they had not managed this, far more users would have either stayed on Steem or moved to some different project entirely.The lesson that we can learn from this situation is this: Steem-the-company never actually "owned" the coins. If they did, they would have had the practical ability to use, enjoy and abuse the coins in whatever way they wanted. But in reality, when the company tried to enjoy and abuse the coins in a way that the community did not like, they were successfully stopped. What's going on here is a pattern of a similar type to what we saw with the not-yet-issued Bitcoin and Ethereum coin rewards: the coins were ultimately owned not by a cryptographic key, but by some kind of social contract.We can apply the same reasoning to many other structures in the blockchain space. Consider, for example, the ENS root multisig. The root multisig is controlled by seven prominent ENS and Ethereum community members. But what would happen if four of them were to come together and "upgrade" the registrar to one that transfers all the best domains to themselves? Within the context of ENS-the-smart-contract-system, they have the complete and unchallengeable ability to do this. But if they actually tried to abuse their technical ability in this way, what would happen is clear to anyone: they would be ostracized from the community, the remaining ENS community members would make a new ENS contract that restores the original domain owners, and every Ethereum application that uses ENS would repoint their UI to use the new one.This goes well beyond smart contract structures. Why is it that Elon Musk can sell an NFT of Elon Musk's tweet, but Jeff Bezos would have a much harder time doing the same? Elon and Jeff have the same level of ability to screenshot Elon's tweet and stick it into an NFT dapp, so what's the difference? To anyone who has even a basic intuitive understanding of human social psychology (or the fake art scene), the answer is obvious: Elon selling Elon's tweet is the real thing, and Jeff doing the same is not. Once again, millions of dollars of value are being controlled and allocated, not by individuals or cryptographic keys, but by social conceptions of legitimacy.And, going even further out, legitimacy governs all sorts of social status games, intellectual discourse, language, property rights, political systems and national borders. Even blockchain consensus works the same way: the only difference between a soft fork that gets accepted by the community and a 51% censorship attack after which the community coordinates an extra-protocol recovery fork to take out the attacker is legitimacy.So what is legitimacy?See also: my earlier post on blockchain governance.To understand the workings of legitimacy, we need to dig down into some game theory. There are many situations in life that demand coordinated behavior: if you act in a certain way alone, you are likely to get nowhere (or worse), but if everyone acts together a desired result can be achieved.An abstract coordination game. You benefit heavily from making the same move as everyone else.One natural example is driving on the left vs right side of the road: it doesn't really matter what side of the road people drive on, as long as they drive on the same side. If you switch sides at the same time as everyone else, and most people prefer the new arrangement, there can be a net benefit. But if you switch sides alone, no matter how much you prefer driving on the other side, the net result for you will be quite negative.Now, we are ready to define legitimacy.Legitimacy is a pattern of higher-order acceptance. An outcome in some social context is legitimate if the people in that social context broadly accept and play their part in enacting that outcome, and each individual person does so because they expect everyone else to do the same.Legitimacy is a phenomenon that arises naturally in coordination games. If you're not in a coordination game, there's no reason to act according to your expectation of how other people will act, and so legitimacy is not important. But as we have seen, coordination games are everywhere in society, and so legitimacy turns out to be quite important indeed. In almost any environment with coordination games that exists for long enough, there inevitably emerge some mechanisms that can choose which decision to take. These mechanisms are powered by an established culture that everyone pays attention to these mechanisms and (usually) does what they say. Each person reasons that because everyone else follows these mechanisms, if they do something different they will only create conflict and suffer, or at least be left in a lonely forked ecosystem all by themselves. If a mechanism successfully has the ability to make these choices, then that mechanism has legitimacy.A Byzantine general rallying his troops forward. The purpose of this isn't just to make the soldiers feel brave and excited, but also to reassure them that everyone else feels brave and excited and will charge forward as well, so an individual soldier is not just committing suicide by charging forward alone.In any context where there's a coordination game that has existed for long enough, there's likely a conception of legitimacy. And blockchains are full of coordination games. Which client software do you run? Which decentralized domain name registry do you ask for which address corresponds to a .eth name? Which copy of the Uniswap contract do you accept as being "the" Uniswap exchange? Even NFTs are a coordination game. The two largest parts of an NFT's value are (i) pride in holding the NFT and ability to show off your ownership, and (ii) the possibility of selling it in the future. For both of these components, it's really really important that whatever NFT you buy is recognized as legitimate by everyone else. In all of these cases, there's a great benefit to having the same answer as everyone else, and the mechanism that determines that equilibrium has a lot of power.Theories of legitimacyThere are many different ways in which legitimacy can come about. In general, legitimacy arises because the thing that gains legitimacy is psychologically appealing to most people. But of course, people's psychological intuitions can be quite complex. It is impossible to make a full listing of theories of legitimacy, but we can start with a few:Legitimacy by brute force: someone convinces everyone that they are powerful enough to impose their will and resisting them will be very hard. This drives most people to submit because each person expects that everyone else will be too scared to resist as well. Legitimacy by continuity: if something was legitimate at time T, it is by default legitimate at time T+1. Legitimacy by fairness: something can become legitimate because it satisfies an intuitive notion of fairness. See also: my post on credible neutrality, though note that this is not the only kind of fairness. Legitimacy by process: if a process is legitimate, the outputs of that process gain legitimacy (eg. laws passed by democracies are sometimes described in this way). Legitimacy by performance: if the outputs of a process lead to results that satisfy people, then that process can gain legitimacy (eg. successful dictatorships are sometimes described in this way). Legitimacy by participation: if people participate in choosing an outcome, they are more likely to consider it legitimate. This is similar to fairness, but not quite: it rests on a psychological desire to be consistent with your previous actions. Note that legitimacy is a descriptive concept; something can be legitimate even if you personally think that it is horrible. That said, if enough people think that an outcome is horrible, there is a higher chance that some event will happen in the future that will cause that legitimacy to go away, often at first gradually, then suddenly.Legitimacy is a powerful social technology, and we should use itThe public goods funding situation in cryptocurrency ecosystems is fairly poor. There are hundreds of billions of dollars of capital flowing around, but public goods that are key to that capital's ongoing survival are receiving only tens of millions of dollars per year of funding.There are two ways to respond to this fact. The first way is to be proud of these limitations and the valiant, even if not particularly effective, efforts that your community makes to work around them. This seems to be the route that the Bitcoin ecosystem often takes: The personal self-sacrifice of the teams funding core development is of course admirable, but it's admirable the same way that Eliud Kipchoge running a marathon in under 2 hours is admirable: it's an impressive show of human fortitude, but it's not the future of transportation (or, in this case, public goods funding). Much like we have much better technologies to allow people to move 42 km in under an hour without exceptional fortitude and years of training, we should also focus on building better social technologies to fund public goods at the scales that we need, and as a systemic part of our economic ecology and not one-off acts of philanthropic initiative.Now, let us get back to cryptocurrency. A major power of cryptocurrency (and other digital assets such as domain names, virtual land and NFTs) is that it allows communities to summon up large amounts of capital without any individual person needing to personally donate that capital. However, this capital is constrained by conceptions of legitimacy: you cannot simply allocate it to a centralized team without compromising on what makes it valuable. While Bitcoin and Ethereum do already rely on conceptions of legitimacy to respond to 51% attacks, using conceptions of legitimacy to guide in-protocol funding of public goods is much harder. But at the increasingly rich application layer where new protocols are constantly being created, we have quite a bit more flexibility in where that funding could go.Legitimacy in BitsharesOne of the long-forgotten, but in my opinion very innovative, ideas from the early cryptocurrency space was the Bitshares social consensus model. Essentially, Bitshares described itself as a community of people (PTS and AGS holders) who were willing to help collectively support an ecosystem of new projects, but for a project to be welcomed into the ecosystem, it would have to allocate 10% of its token supply to existing PTS and AGS holders.Now, of course anyone can make a project that does not allocate any coins to PTS/AGS holders, or even fork a project that did make an allocation and take the allocation out. But, as Dan Larimer says:You cannot force anyone to do anything, but in this market is is all network effect. If someone comes up with a compelling implementation then you can adopt the entire PTS community for the cost of generating a new genesis block. The individual who decided to start from scratch would have to build an entire new community around his system. Considering the network effect, I suspect that the coin that honors ProtoShares will win.This is also a conception of legitimacy: any project that makes the allocation to PTS/AGS holders will get the attention and support of the community (and it will be worthwhile for each individual community member to take an interest in the project because the rest of the community is doing so as well), and any project that does not make the allocation will not. Now, this is certainly not a conception of legitimacy that we want to replicate verbatim - there is little appetite in the Ethereum community for enriching a small group of early adopters - but the core concept can be adapted into something much more socially valuable.Extending the model to EthereumBlockchain ecosystems, Ethereum included, value freedom and decentralization. But the public goods ecology of most of these blockchains is, regrettably, still quite authority-driven and centralized: whether it's Ethereum, Zcash or any other major blockchain, there is typically one (or at most 2-3) entities that far outspend everyone else, giving independent teams that want to build public goods few options. I call this model of public goods funding "Central Capital Coordinators for Public-goods" (CCCPs). This state of affairs is not the fault of the organizations themselves, who are typically valiantly doing their best to support the ecosystem. Rather, it's the rules of the ecosystem that are being unfair to that organization, because they hold the organization to an unfairly high standard. Any single centralized organization will inevitably have blindspots and at least a few categories and teams whose value that it fails to understand; this is not because anyone involved is doing anything wrong, but because such perfection is beyond the reach of small groups of humans. So there is great value in creating a more diversified and resilient approach to public goods funding to take the pressure off any single organization.Fortunately, we already have the seed of such an alternative! The Ethereum application-layer ecosystem exists, is growing increasingly powerful, and is already showing its public-spiritedness. Companies like Gnosis have been contributing to Ethereum client development, and various Ethereum DeFi projects have donated hundreds of thousands of dollars to the Gitcoin Grants matching pool.Gitcoin Grants has already achieved a high level of legitimacy: its public goods funding mechanism, quadratic funding, has proven itself to be credibly neutral and effective at reflecting the community's priorities and values and plugging the holes left by existing funding mechanisms. Sometimes, top Gitcoin Grants matching recipients are even used as inspiration for grants by other and more centralized grant-giving entities. The Ethereum Foundation itself has played a key role in supporting this experimentation and diversity, incubating efforts like Gitcoin Grants, along with MolochDAO and others, that then go on to get broader community support.We can make this nascent public goods-funding ecosystem even stronger by taking the Bitshares model, and making a modification: instead of giving the strongest community support to projects who allocate tokens to a small oligarchy who bought PTS or AGS back in 2013, we support projects that contribute a small portion of their treasuries toward the public goods that make them and the ecosystem that they depend on possible. And, crucially, we can deny these benefits to projects that fork an existing project and do not give back value to the broader ecosystem.There are many ways to do support public goods: making a long-term commitment to support the Gitcoin Grants matching pool, supporting Ethereum client development (also a reasonably credibly-neutral task as there's a clear definition of what an Ethereum client is), or even running one's own grant program whose scope goes beyond that particular application-layer project itself. The easiest way to agree on what counts as sufficient support is to agree on how much - for example, 5% of a project's spending going to support the broader ecosystem and another 1% going to public goods that go beyond the blockchain space - and rely on good faith to choose where that funding would go.Does the community actually have that much leverage?Of course, there are limits to the value of this kind of community support. If a competing project (or even a fork of an existing project) gives its users a much better offering, then users are going to flock to it, regardless of how many people yell at them to instead use some alternative that they consider to be more pro-social.But these limits are different in different contexts; sometimes the community's leverage is weak, but at other times it's quite strong. An interesting case study in this regard is the case of Tether vs DAI. Tether has many scandals, but despite this traders use Tether to hold and move around dollars all the time. The more decentralized and transparent DAI, despite its benefits, is unable to take away much of Tether's market share, at least as far as traders go. But where DAI excels is applications: Augur uses DAI, xDai uses DAI, PoolTogether uses DAI, zk.money plans to use DAI, and the list goes on. What dapps use USDT? Far fewer.Hence, though the power of community-driven legitimacy effects is not infinite, there is nevertheless considerable room for leverage, enough to encourage projects to direct at least a few percent of their budgets to the broader ecosystem. There's even a selfish reason to participate in this equilibrium: if you were the developer of an Ethereum wallet, or an author of a podcast or newsletter, and you saw two competing projects, one of which contributes significantly to ecosystem-level public goods including yourself and one which does not, for which one would you do your utmost to help them secure more market share?NFTs: supporting public goods beyond EthereumThe concept of supporting public goods through value generated "out of the ether" by publicly supported conceptions of legitimacy has value going far beyond the Ethereum ecosystem. An important and immediate challenge and opportunity is NFTs. NFTs stand a great chance of significantly helping many kinds of public goods, especially of the creative variety, at least partially solve their chronic and systemic funding deficiencies. Actually a very admirable first step.But they could also be a missed opportunity: there is little social value in helping Elon Musk earn yet another $1 million by selling his tweet when, as far as we can tell, the money is just going to himself (and, to his credit, he eventually decided not to sell). If NFTs simply become a casino that largely benefits already-wealthy celebrities, that would be a far less interesting outcome.Fortunately, we have the ability to help shape the outcome. Which NFTs people find attractive to buy, and which ones they do not, is a question of legitimacy: if everyone agrees that one NFT is interesting and another NFT is lame, then people will strongly prefer buying the first, because it would have both higher value for bragging rights and personal pride in holding it, and because it could be resold for more because everyone else is thinking in the same way. If the conception of legitimacy for NFTs can be pulled in a good direction, there is an opportunity to establish a solid channel of funding to artists, charities and others.Here are two potential ideas:Some institution (or even DAO) could "bless" NFTs in exchange for a guarantee that some portion of the revenues goes toward a charitable cause, ensuring that multiple groups benefit at the same time. This blessing could even come with an official categorization: is the NFT dedicated to global poverty relief, scientific research, creative arts, local journalism, open source software development, empowering marginalized communities, or something else? We can work with social media platforms to make NFTs more visible on people's profiles, giving buyers a way to show the values that they committed not just their words but their hard-earned money to. This could be combined with (1) to nudge users toward NFTs that contribute to valuable social causes. There are definitely more ideas, but this is an area that certainly deserves more active coordination and thought.In summaryThe concept of legitimacy (higher-order acceptance) is very powerful. Legitimacy appears in any context where there is coordination, and especially on the internet, coordination is everywhere. There are different ways in which legitimacy comes to be: brute force, continuity, fairness, process, performance and participation are among the important ones. Cryptocurrency is powerful because it lets us summon up large pools of capital by collective economic will, and these pools of capital are, at the beginning, not controlled by any person. Rather, these pools of capital are controlled directly by concepts of legitimacy. It's too risky to start doing public goods funding by printing tokens at the base layer. Fortunately, however, Ethereum has a very rich application-layer ecosystem, where we have much more flexibility. This is in part because there's an opportunity not just to influence existing projects, but also shape new ones that will come into existence in the future. Application-layer projects that support public goods in the community should get the support of the community, and this is a big deal. The example of DAI shows that this support really matters! The Etherem ecosystem cares about mechanism design and innovating at the social layer. The Ethereum ecosystem's own public goods funding challenges are a great place to start! But this goes far beyond just Ethereum itself. NFTs are one example of a large pool of capital that depends on concepts of legitimacy. The NFT industry could be a significant boon to artists, charities and other public goods providers far beyond our own virtual corner of the world, but this outcome is not predetermined; it depends on active coordination and support.

Prediction Markets: Tales from the Election Prediction Markets: Tales from the Election2021 Feb 18 See all posts Prediction Markets: Tales from the Election Special thanks to Jeff Coleman, Karl Floersch and Robin Hanson for critical feedback and review.Trigger warning: I express some political opinions.Prediction markets are a subject that has interested me for many years. The idea of allowing anyone in the public to make bets about future events, and using the odds at which these bets are made as a credibly neutral source of predicted probabilities of these events, is a fascinating application of mechanism design. Closely related ideas, like futarchy, have always interested me as innovative tools that could improve governance and decision-making. And as Augur and Omen, and more recently PolyMarket, have shown, prediction markets are a fascinating application of blockchains (in all three cases, Ethereum) as well.And the 2020 US presidential election, it seems like prediction markets are finally entering the limelight, with blockchain-based markets in particular growing from near-zero in 2016 to millions of dollars of volume in 2020. As someone who is closely interested in seeing Ethereum applications cross the chasm into widespread adoption, this of course aroused my interest. At first, I was inclined to simply watch, and not participate myself: I am not an expert on US electoral politics, so why should I expect my opinion to be more correct than that of everyone else who was already trading? But in my Twitter-sphere, I saw more and more arguments from Very Smart People whom I respected arguing that the markets were in fact being irrational and I should participate and bet against them if I can. Eventually, I was convinced.I decided to make an experiment on the blockchain that I helped to create: I bought $2,000 worth of NTRUMP (tokens that pay $1 if Trump loses) on Augur. Little did I know then that my position would eventually increase to $308,249, earning me a profit of over $56,803, and that I would make all of these remaining bets, against willing counterparties, after Trump had already lost the election. What would transpire over the next two months would prove to be a fascinating case study in social psychology, expertise, arbitrage, and the limits of market efficiency, with important ramifications to anyone who is deeply interested in the possibilities of economic institution design.Before the Election My first bet on this election was actually not on a blockchain at all. When Kanye announced his presidential bid in July, a political theorist whom I ordinarily quite respect for his high-quality and original thinking immediately claimed on Twitter that he was confident that this would split the anti-Trump vote and lead to a Trump victory. I remember thinking at the time that this particular opinion of his was over-confident, perhaps even a result of over-internalizing the heuristic that if a viewpoint seems clever and contrarian then it is likely to be correct. So of course I offered to make a $200 bet, myself betting the boring conventional pro-Biden view, and he honorably accepted.The election came up again on my radar in September, and this time it was the prediction markets that caught my attention. The markets gave Trump a nearly 50% chance of winning, but I saw many Very Smart People in my Twitter-sphere whom I respected pointing out that this number seemed far too high. This of course led to the familiar "efficient markets debate": if you can buy a token that gives you $1 if Trump loses for $0.52, and Trump's actual chance of losing is much higher, why wouldn't people just come in and buy the token until the price rises more? And if nobody has done this, who are you to think that you're smarter than everyone else?Ne0liberal's Twitter thread just before Election Day does an excellent job summarizing his case against prediction markets being accurate at that time. In short, the (non-blockchain) prediction markets that most people used at least prior to 2020 have all sorts of restrictions that make it difficult for people to participate with more than a small amount of cash. As a result, if a very smart individual or a professional organization saw a probability that they believed was wrong, they would only have a very limited ability to push the price in the direction that they believe to be correct.The most important restrictions that the paper points out are:Low limits (well under $1,000) on how much each person can bet High fees (eg. a 5% withdrawal fee on PredictIt) And this is where I pushed back against ne0liberal in September: although the stodgy old-world centralized prediction markets may have low limits and high fees, the crypto markets do not! On Augur or Omen, there's no limit to how much someone can buy or sell if they think the price of some outcome token is too low or too high. And the blockchain-based prediction markets were following the same prices as PredictIt. If the markets really were over-estimating Trump because high fees and low trading limits were preventing the more cool-headed traders from outbidding the overly optimistic ones, then why would blockchain-based markets, which don't have those issues, show the same prices? PredictIt Augur The main response my Twitter friends gave to this was that blockchain-based markets are highly niche, and very few people, particularly very few people who know much about politics, have easy access to cryptocurrency. That seemed plausible, but I was not too confident in that argument. And so I bet $2,000 against Trump and went no further.The ElectionThen the election happened. After an initial scare where Trump at first won more seats than we expected, Biden turned out to be the eventual winner. Whether or not the election itself validated or refuted the efficiency of prediction markets is a topic that, as far as I can tell, is quite open to interpretation. On the one hand, by a standard Bayes rule application, I should decrease my confidence of prediction markets, at least relative to Nate Silver. Prediction markets gave a 60% chance of Biden winning, Nate Silver gave a 90% chance of Biden winning. Since Biden in fact won, this is one piece of evidence that I live in a world where Nate gives the more correct answers.But on the other hand, you can make a case that the prediction markets bettter estimated the margin of victory. The median of Nate's probability distribution was somewhere around 370 of 538 electoral college votes going to Biden: The Trump markets didn't give a probability distribution, but if you had to guess a probability distribution from the statistic "40% chance Trump will win", you would probably give one with a median somewhere around 300 EC votes for Biden. The actual result: 306. So the net score for prediction markets vs Nate seems to me, on reflection, ambiguous.After the electionBut what I could not have imagined at the time was that the election itself was just the beginning. A few days after the election, Biden was declared the winner by various major organizations and even a few foreign governments. Trump mounted various legal challenges to the election results, as was expected, but each of these challenges quickly failed. But for over a month, the price of the NTRUMP tokens stayed at 85 cents!At the beginning, it seemed reasonable to guess that Trump had a 15% chance of overturning the results; after all, he had appointed three judges to the Supreme Court, at a time of heightened partisanship where many have come to favor team over principle. Over the next three weeks, however, it became more and more clear that the challenges were failing, and Trump's hopes continued to look grimmer with each passing day, but the NTRUMP price did not budge; in fact, it even briefly decreased to around $0.82. On December 11, more than five weeks after the election, the Supreme Court decisively and unanimously rejected Trump's attempts to overturn the vote, and the NTRUMP price finally rose.... to $0.88.It was in November that I was finally convinced that the market skeptics were right, and I plunged in and bet against Trump myself. The decision was not so much about the money; after all, barely two months later I would earn and donate to GiveDirectly a far larger amount simply from holding dogecoin. Rather, it was to take part in the experiment not just as an observer, but as an active participant, and improve my personal understanding of why everyone else hadn't already plunged in to buy NTRUMP tokens before me.Dipping inI bought my NTRUMP on Catnip, a front-end user interface that combines together the Augur prediction market with Balancer, a Uniswap-style constant-function market maker. Catnip was by far the easiest interface for making these trades, and in my opinion contributed significantly to Augur's usability.There are two ways to bet against Trump with Catnip:Use DAI to buy NTRUMP on Catnip directly Use Foundry to access an Augur feature that allows you to convert 1 DAI into 1 NTRUMP + 1 YTUMP + 1ITRUMP (the "I" stands for "invalid", more on this later), and sell the YTRUMP on Catnip At first, I only knew about the first option. But then I discovered that Balancer has far more liquidity for YTRUMP, and so I switched to the second option.There was also another problem: I did not have any DAI. I had ETH, and I could have sold my ETH to get DAI, but I did not want to sacrifice my ETH exposure; it would have been a shame if I earned $50,000 betting against Trump but simultaneously lost $500,000 missing out on ETH price changes. So I decided to keep my ETH price exposure the same by opening up a collateralized debt position (CDP, now also called a "vault") on MakerDAO.A CDP is how all DAI is generated: users deposit their ETH into a smart contract, and are allowed to withdraw an amount of newly-generated DAI up to 2/3 of the value of ETH that they put in. They can get their ETH back by sending back the same amount of DAI that they withdrew plus an extra interest fee (currently 3.5%). If the value of the ETH collateral that you deposited drops to less than 150% the value of the DAI you withdrew, anyone can come in and "liquidate" the vault, forcibly selling the ETH to buy back the DAI and charging you a high penalty. Hence, it's a good idea to have a high collateralization ratio in case of sudden price movements; I had over $3 worth of ETH in my CDP for every $1 that I withdrew.Recapping the above, here's the pipeline in diagram form: I did this many times; the slippage on Catnip meant that I could normally make trades only up to about $5,000 to $10,000 at a time without prices becoming too unfavorable (when I had skipped Foundry and bought NTRUMP with DAI directly, the limit was closer to $1,000). And after two months, I had accumulated over 367,000 NTRUMP.Why not everyone else?Before I went in, I had four main hypotheses about why so few others were buying up dollars for 85 cents:Fear that either the Augur smart contracts would break or Trump supporters would manipulate the oracle (a decentralized mechanism where holders of Augur's REP token vote by staking their tokens on one outcome or the other) to make it return a false result Capital costs: to buy these tokens, you have to lock up funds for over two months, and this removes your ability to spend those funds or make other profitable trades for that duration It's too technically complicated for almost everyone to trade There just really are far fewer people than I thought who are actually motivated enough to take a weird opportunity even when it presents them straight in the face All four have reasonable arguments going for them. Smart contracts breaking is a real risk, and the Augur oracle had not before been tested in such a contentious environment. Capital costs are real, and while betting against something is easier in a prediction market than in a stock market because you know that prices will never go above $1, locking up capital nevertheless competes with other lucrative opportunities in the crypto markets. Making transactions things in dapps is technically complicated, and it's rational to have some degree of fear-of-the-unknown.But my experience actually going into the financial trenches, and watching the prices on this market evolve, taught me a lot about each of these hypotheses.Fear of smart contract exploitsAt first, I thought that "fear of smart contract exploits" must have been a significant part of the explanation. But over time, I have become more convinced that it is probably not a dominant factor. One way to see why I think this is the case is to compare the prices for YTRUMP and ITRUMP. ITRUMP stands for "Invalid Trump"; "Invalid" is an event outcome that is intended to be triggered in some exceptional cases: when the description of the event is ambiguous, when the outcome of the event is not yet known when the market is resolved, when the market is unethical (eg. assassination markets), and a few other similar situations. In this market, the price of ITRUMP consistently stayed under $0.02. If someone wanted to earn a profit by attacking the market, it would be far more lucrative for them to not buy YTRUMP at $0.15, but instead buy ITRUMP at $0.02. If they buy a large amount of ITRUMP, they could earn a 50x return if they can force the "invalid" outcome to actually trigger. So if you fear an attack, buying ITRUMP is by far the most rational response. And yet, very few people did.A further argument against fear of smart contract exploits, of course, is the fact that in every crypto application except prediction markets (eg. Compound, the various yield farming schemes) people are surprisingly blasé about smart contract risks. If people are willing to put their money into all sorts of risky and untested schemes even for a promise of mere 5-8% annual gains, why would they suddenly become over-cautious here?Capital costsCapital costs - the inconvenience and opportunity cost of locking up large amounts of money - are a challenge that I have come to appreciate much more than I did before. Just looking at the Augur side of things, I needed to lock up 308,249 DAI for an average of about two months to make a $56,803 profit. This works out to about a 175% annualized interest rate; so far, quite a good deal, even compared to the various yield farming crazes of the summer of 2020. But this becomes worse when you take into account what I needed to do on MakerDAO. Because I wanted to keep my exposure to ETH the same, I needed to get my DAI through a CDP, and safely using a CDP required a collateral ratio of over 3x. Hence, the total amount of capital I actually needed to lock up was somewhere around a million dollars. Now, the interest rates are looking less favorable. And if you add to that the possibility, however remote, that a smart contract hack, or a truly unprecedented political event, actually will happen, it looks less favorable still.But even still, assuming a 3x lockup and a 3% chance of Augur breaking (I had bought ITRUMP to cover the possibility that it breaks in the "invalid" direction, so I needed only worry about the risk of breaks in the "yes" direction or the the funds being stolen outright), that works out to a risk-neutral rate of about 35%, and even lower once you take real human beings' views on risk into account. The deal is still very attractive, but on the other hand, it now looks very understandable that such numbers are unimpressive to people who live and breathe cryptocurrency with its frequent 100x ups and downs.Trump supporters, on the other hand, faced none of these challenges: they cancelled out my $308,249 bet by throwing in a mere $60,000 (my winnings are less than this because of fees). When probabilities are close to 0 or 1, as is the case here, the game is very lopsided in favor of those who are trying to push the probability away from the extreme value. And this explains not just Trump; it's also the reason why all sorts of popular-among-a-niche candidates with no real chance of victory frequently get winning probabilities as high as 5%.Technical complexityI had at first tried buying NTRUMP on Augur, but technical glitches in the user interface prevented me from being able to make orders on Augur directly (other people I talked to did not have this issue... I am still not sure what happened there). Catnip's UI is much simpler and worked excellently. However, automated market makers like Balancer (and Uniswap) work best for smaller trades; for larger trades, the slippage is too high. This is a good microcosm of the broader "AMM vs order book" debate: AMMs are more convenient but order books really do work better for large trades. Uniswap v3 is introducing an AMM design that has better capital efficiency; we shall see if that improves things.There were other technical complexities too, though fortunately they all seem to be easily solvable. There is no reason why an interface like Catnip could not integrate the "DAI -> Foundry -> sell YTRUMP" path into a contract so that you could buy NTRUMP that way in a single transaction. In fact, the interface could even check the price and liquidity properties of the "DAI -> NTRUMP" path and the "DAI -> Foundry -> sell YTRUMP" path and give you the better trade automatically. Even withdrawing DAI from a MakerDAO CDP can be included in that path. My conclusion here is optimistic: technical complexity issues were a real barrier to participation this round, but things will be much easier in future rounds as technology improves.Intellectual underconfidenceAnd now we have the final possibility: that many people (and smart people in particular) have a pathology that they suffer from excessive humility, and too easily conclude that if no one else has taken some action, then there must therefore be a good reason why that action is not worth taking.Eliezer Yudkowsky spends the second half of his excellent book Inadequate Equilibria making this case, arguing that too many people overuse "modest epistemology", and we should be much more willing to act on the results of our reasoning, even when the result suggests that the great majority of the population is irrational or lazy or wrong about something. When I read those sections for the first time, I was unconvinced; it seemed like Eliezer was simply being overly arrogant. But having gone through this experience, I have come to see some wisdom in his position.This was not my first time seeing the virtues of trusting one's own reasoning first hand. When I had originally started working on Ethereum, I was at first beset by fear that there must be some very good reason the project was doomed to fail. A fully programmable smart-contract-capable blockchain, I reasoned, was clearly such a great improvement over what came before, that surely many other people must have thought of it before I did. And so I fully expected that, as soon as I publish the idea, many very smart cryptographers would tell me the very good reasons why something like Ethereum was fundamentally impossible. And yet, no one ever did.Of course, not everyone suffers from excessive modesty. Many of the people making predictions in favor of Trump winning the election were arguably fooled by their own excessive contrarianism. Ethereum benefited from my youthful suppression of my own modesty and fears, but there are plenty of other projects that could have benefited from more intellectual humility and avoided failures. Not a sufferer of excessive modesty.But nevertheless it seems to me more true than ever that, as goes the famous Yeats quote, "the best lack all conviction, while the worst are full of passionate intensity." Whatever the faults of overconfidence or contrarianism sometimes may be, it seems clear to me that spreading a society-wide message that the solution is to simply trust the existing outputs of society, whether those come in the form of academic institutions, media, governments or markets, is not the solution. All of these institutions can only work precisely because of the presence of individuals who think that they do not work, or who at least think that they can be wrong at least some of the time.Lessons for futarchySeeing the importance of capital costs and their interplay with risks first hand is also important evidence for judging systems like futarchy. Futarchy, and "decision markets" more generally are an important and potentially very socially useful application of prediction markets. There is not much social value in having slightly more accurate predictions of who will be the next president. But there is a lot of social value in having conditional predictions: if we do A, what's the chance it will lead to some good thing X, and if we do B instead what are the chances then? Conditional predictions are important because they do not just satisfy our curiosity; they can also help us make decisions.Though electoral prediction markets are much less useful than conditional predictions, they can help shed light on an important question: how robust are they to manipulation or even just biased and wrong opinions? We can answer this question by looking at how difficult arbitrage is: suppose that a conditional prediction market currently gives probabilities that (in your opinion) are wrong (could be because of ill-informed traders or an explicit manipulation attempt; we don't really care). How much of an impact can you have, and how much profit can you make, by setting things right?Let's start with a concrete example. Suppose that we are trying to use a prediction market to choose between decision A and decision B, where each decision has some probability of achieving some desirable outcome. Suppose that your opinion is that decision A has a 50% chance of achieving the goal, and decision B has a 45% chance. The market, however, (in your opinion wrongly) thinks decision B has a 55% chance and decision A has a 40% chance.Probability of good outcome if we choose strategy... Current market position Your opinion A 40% 50% B 55% 45% Suppose that you are a small participant, so your individual bets won't affect the outcome; only many bettors acting together could. How much of your money should you bet?The standard theory here relies on the Kelly criterion. Essentially, you should act to maximize the expected logarithm of your assets. In this case, we can solve the resulting equation. Suppose you invest portion \(r\) of your money into buying A-token for $0.4. Your expected new log-wealth, from your point of view, would be:\(0.5 * log((1-r) + \frac) + 0.5 * log(1-r)\)The first term is the 50% chance (from your point of view) that the bet pays off, and the portion \(r\) that you invest grows by 2.5x (as you bought dollars at 40 cents). The second term is the 50% chance that the bet does not pay off, and you lose the portion you bet. We can use calculus to find the \(r\) that maximizes this; for the lazy, here's WolframAlpha. The answer is \(r = \frac\). If other people buy and the price for A on the market gets up to 47% (and B gets down to 48%), we can redo the calculation for the last trader who would flip the market over to make it correctly favor A:\(0.5 * log((1-r) + \frac) + 0.5 * log(1-r)\)Here, the expected-log-wealth-maximizing \(r\) is a mere 0.0566. The conclusion is clear: when decisions are close and when there is a lot of noise, it turns out that it only makes sense to invest a small portion of your money in a market. And this is assuming rationality; most people invest less into uncertain gambles than the Kelly criterion says they should. Capital costs stack on top even further. But if an attacker really wants to force outcome B through because they want it to happen for personal reasons, they can simply put all of their capital toward buying that token. All in all, the game can easily be lopsided more than 20:1 in favor of the attacker.Of course, in reality attackers are rarely willing to stake all their funds on one decision. And futarchy is not the only mechanism that is vulerable to attacks: stock markets are similarly vulnerable, and non-market decision mechanisms can also be manipulated by determined wealthy attackers in all sorts of ways. But nevertheless, we should be wary of assuming that futarchy will propel us to new heights of decision-making accuracy.Interestingly enough, the math seems to suggest that futarchy would work best when the expected manipulators would want to push the outcome toward an extreme value. An example of this might be liability insurance, as someone wishing to improperly obtain insurance would effectively be trying to force the market-estimated probability that an unfavorable event will happen down to zero. And as it turns out, liability insurance is futarchy inventor Robin Hanson's new favorite policy prescription.Can prediction markets become better?The final question to ask is: are prediction markets doomed to repeat errors as grave as giving Trump a 15% chance of overturning the election in early December, and a 12% chance of overturning it even after the Supreme Court including three judges whom he appointed telling him to screw off? Or could the markets improve over time? My answer is, surprisingly, emphatically on the optimistic side, and I see a few reasons for optimism.Markets as natural selectionFirst, these events have given me a new perspective on how market efficiency and rationality might actually come about. Too often, proponents of market efficiency theories claim that market efficiency results because most participants are rational (or at least the rationals outweigh any coherent group of deluded people), and this is true as an axiom. But instead, we could take an evolutionary perspective on what is going on.Crypto is a young ecosystem. It is an ecosystem that is still quite disconnected from the mainstream, Elon's recent tweets notwithstanding, and that does not yet have much expertise in the minutiae of electoral politics. Those who are experts in electoral politics have a hard time getting into crypto, and crypto has a large presence of not-always-correct forms of contrarianism especially when it comes to politics. But what happened this year is that within the crypto space, prediction market users who correctly expected Biden to win got an 18% increase to their capital, and prediction market users who incorrectly expected Trump to win got a 100% decrease to their capital (or at least the portion they put into the bet). Thus, there is a selection pressure in favor of the type of people who make bets that turn out to be correct. After ten rounds of this, good predictors will have more capital to bet with, and bad predictors will have less capital to bet with. This does not rely on anyone "getting wiser" or "learning their lesson" or any other assumption about humans' capacity to reason and learn. It is simply a result of selection dynamics that over time, participants that are good at making correct guesses will come to dominate the ecosystem.Note that prediction markets fare better than stock markets in this regard: the "nouveau riche" of stock markets often arise from getting lucky on a single thousandfold gain, adding a lot of noise to the signal, but in prediction markets, prices are bounded between 0 and 1, limiting the impact of any one single event.Better participants and better technologySecond, prediction markets themselves will improve. User interfaces have greatly improved already, and will continue to improve further. The complexity of the MakerDAO -> Foundry -> Catnip cycle will be abstracted away into a single transaction. Blockchain scaling technology will improve, reducing fees for participants (The ZK-rollup Loopring with a built-in AMM is already live on the Ethereum mainnet, and a prediction market could theoretically run on it).Third, the demonstration that we saw of the prediction market working correctly will ease participants' fears. Users will see that the Augur oracle is capable of giving correct outputs even in very contentious situations (this time, there were two rounds of disputes, but the no side nevertheless cleanly won). People from outside the crypto space will see that the process works and be more inclined to participate. Perhaps even Nate Silver himself might get some DAI and use Augur, Omen, Polymarket and other markets to supplement his income in 2022 and beyond.Fourth, prediction market tech itself could improve. Here is a proposal from myself on a market design that could make it more capital-efficient to simultaneously bet against many unlikely events, helping to prevent unlikely outcomes from getting irrationally high odds. Other ideas will surely spring up, and I look forward to seeing more experimentation in this direction.ConclusionThis whole saga has proven to be an incredibly interesting direct trial-by-first test of prediction markets and how they collide with the complexities of individual and social psychology. It shows a lot about how market efficiency actually works in practice, what are the limits of it and what could be done to improve it.It has also been an excellent demonstration of the power of blockchains; in fact, it is one of the Ethereum applications that have provided to me the most concrete value. Blockchains are often criticized for being speculative toys and not doing anything meaningful except for self-referential games (tokens, with yield farming, whose returns are powered by... the launch of other tokens). There are certainly exceptions that the critics fail to recognize; I personally have benefited from ENS and even from using ETH for payments on several occasions where all credit card options failed. But over the last few months, it seems like we have seen a rapid burst in Ethereum applications being concretely useful for people and interacting with the real world, and prediction markets are a key example of this.I expect prediction markets to become an increasingly important Ethereum application in the years to come. The 2020 election was only the beginning; I expect more interest in prediction markets going forward, not just for elections but for conditional predictions, decision-making and other applications as well. The amazing promises of what prediction markets could bring if they work mathematically optimally will, of course, continue to collide with the limits of human reality, and hopefully, over time, we will get a much clearer view of exactly where this new social technology can provide the most value.

An approximate introduction to how zk-SNARKs are possible An approximate introduction to how zk-SNARKs are possible2021 Jan 26 See all posts An approximate introduction to how zk-SNARKs are possible Special thanks to Dankrad Feist, Karl Floersch and Hsiao-wei Wang for feedback and review.Perhaps the most powerful cryptographic technology to come out of the last decade is general-purpose succinct zero knowledge proofs, usually called zk-SNARKs ("zero knowledge succinct arguments of knowledge"). A zk-SNARK allows you to generate a proof that some computation has some particular output, in such a way that the proof can be verified extremely quickly even if the underlying computation takes a very long time to run. The "ZK" ("zero knowledge") part adds an additional feature: the proof can keep some of the inputs to the computation hidden.For example, you can make a proof for the statement "I know a secret number such that if you take the word ‘cow', add the number to the end, and SHA256 hash it 100 million times, the output starts with 0x57d00485aa". The verifier can verify the proof far more quickly than it would take for them to run 100 million hashes themselves, and the proof would also not reveal what the secret number is.In the context of blockchains, this has two very powerful applications:Scalability: if a block takes a long time to verify, one person can verify it and generate a proof, and everyone else can just quickly verify the proof instead Privacy: you can prove that you have the right to transfer some asset (you received it, and you didn't already transfer it) without revealing the link to which asset you received. This ensures security without unduly leaking information about who is transacting with whom to the public. But zk-SNARKs are quite complex; indeed, as recently as in 2014-17 they were still frequently called "moon math". The good news is that since then, the protocols have become simpler and our understanding of them has become much better. This post will try to explain how ZK-SNARKs work, in a way that should be understandable to someone with a medium level of understanding of mathematics.Note that we will focus on scalability; privacy for these protocols is actually relatively easy once the scalability is there, so we will get back to that topic at the end.Why ZK-SNARKs "should" be hardLet us take the example that we started with: we have a number (we can encode "cow" followed by the secret input as an integer), we take the SHA256 hash of that number, then we do that again another 99,999,999 times, we get the output, and we check what its starting digits are. This is a huge computation.A "succinct" proof is one where both the size of the proof and the time required to verify it grow much more slowly than the computation to be verified. If we want a "succinct" proof, we cannot require the verifier to do some work per round of hashing (because then the verification time would be proportional to the computation). Instead, the verifier must somehow check the whole computation without peeking into each individual piece of the computation.One natural technique is random sampling: how about we just have the verifier peek into the computation in 500 different places, check that those parts are correct, and if all 500 checks pass then assume that the rest of the computation must with high probability be fine, too?Such a procedure could even be turned into a non-interactive proof using the Fiat-Shamir heuristic: the prover computes a Merkle root of the computation, uses the Merkle root to pseudorandomly choose 500 indices, and provides the 500 corresponding Merkle branches of the data. The key idea is that the prover does not know which branches they will need to reveal until they have already "committed to" the data. If a malicious prover tries to fudge the data after learning which indices are going to be checked, that would change the Merkle root, which would result in a new set of random indices, which would require fudging the data again... trapping the malicious prover in an endless cycle.But unfortunately there is a fatal flaw in naively applying random sampling to spot-check a computation in this way: computation is inherently fragile. If a malicious prover flips one bit somewhere in the middle of a computation, they can make it give a completely different result, and a random sampling verifier would almost never find out. It only takes one deliberately inserted error, that a random check would almost never catch, to make a computation give a completely incorrect result.If tasked with the problem of coming up with a zk-SNARK protocol, many people would make their way to this point and then get stuck and give up. How can a verifier possibly check every single piece of the computation, without looking at each piece of the computation individually? But it turns out that there is a clever solution.PolynomialsPolynomials are a special class of algebraic expressions of the form:\(x + 5\) \(x^4\) \(x^3 + 3x^2 + 3x + 1\) \(628x^ + 318x^ + 530x^ + ... + 69x + 381\) i.e. they are a sum of any (finite!) number of terms of the form \(c x^k\).There are many things that are fascinating about polynomials. But here we are going to zoom in on a particular one: polynomials are a single mathematical object that can contain an unbounded amount of information (think of them as a list of integers and this is obvious). The fourth example above contained 816 digits of tau, and one can easily imagine a polynomial that contains far more.Furthermore, a single equation between polynomials can represent an unbounded number of equations between numbers. For example, consider the equation \(A(x) + B(x) = C(x)\). If this equation is true, then it's also true that:\(A(0) + B(0) = C(0)\) \(A(1) + B(1) = C(1)\) \(A(2) + B(2) = C(2)\) \(A(3) + B(3) = C(3)\) And so on for every possible coordinate. You can even construct polynomials to deliberately represent sets of numbers so you can check many equations all at once. For example, suppose that you wanted to check:12 + 1 = 13 10 + 8 = 18 15 + 8 = 23 15 + 13 = 28 You can use a procedure called Lagrange interpolation to construct polynomials \(A(x)\) that give (12, 10, 15, 15) as outputs at some specific set of coordinates (eg. (0, 1, 2, 3)), \(B(x)\) the outputs (1, 8, 8, 13) on those same coordinates, and so forth. In fact, here are the polynomials:\(A(x) = -2x^3 + \fracx^2 - \fracx + 12\) \(B(x) = 2x^3 - \fracx^2 + \fracx + 1\) \(C(x) = 5x + 13\) Checking the equation \(A(x) + B(x) = C(x)\) with these polynomials checks all four above equations at the same time.Comparing a polynomial to itselfYou can even check relationships between a large number of adjacent evaluations of the same polynomial using a simple polynomial equation. This is slightly more advanced. Suppose that you want to check that, for a given polynomial \(F\), \(F(x+2) = F(x) + F(x+1)\) within the integer range \(\\) (so if you also check \(F(0) = F(1) = 1\), then \(F(100)\) would be the 100th Fibonacci number).As polynomials, \(F(x+2) - F(x+1) - F(x)\) would not be exactly zero, as it could give arbitrary answers outside the range \(x = \\). But we can do something clever. In general, there is a rule that if a polynomial \(P\) is zero across some set \(S=\\) then it can be expressed as \(P(x) = Z(x) * H(x)\), where \(Z(x) =\) \((x - x_1) * (x - x_2) * ... * (x - x_n)\) and \(H(x)\) is also a polynomial. In other words, any polynomial that equals zero across some set is a (polynomial) multiple of the simplest (lowest-degree) polynomial that equals zero across that same set.Why is this the case? It is a nice corollary of polynomial long division: the factor theorem. We know that, when dividing \(P(x)\) by \(Z(x)\), we will get a quotient \(Q(x)\) and a remainer \(R(x)\) which satisfy \(P(x) = Z(x) * Q(x) + R(x)\), where the degree of the remainder \(R(x)\) is strictly less than that of \(Z(x)\). Since we know that \(P\) is zero on all of \(S\), it means that \(R\) has to be zero on all of \(S\) as well. So we can simply compute \(R(x)\) via polynomial interpolation, since it's a polynomial of degree at most \(n-1\) and we know \(n\) values (the zeroes at \(S\)). Interpolating a polynomial with all zeroes gives the zero polynomial, thus \(R(x) = 0\) and \(H(x)= Q(x)\).Going back to our example, if we have a polynomial \(F\) that encodes Fibonacci numbers (so \(F(x+2) = F(x) + F(x+1)\) across \(x = \\)), then I can convince you that \(F\) actually satisfies this condition by proving that the polynomial \(P(x) =\) \(F(x+2) - F(x+1) - F(x)\) is zero over that range, by giving you the quotient:\(H(x) = \frac\)Where \(Z(x) = (x - 0) * (x - 1) * ... * (x - 98)\).You can calculate \(Z(x)\) yourself (ideally you would have it precomputed), check the equation, and if the check passes then \(F(x)\) satisfies the condition!Now, step back and notice what we did here. We converted a 100-step-long computation (computing the 100th Fibonacci number) into a single equation with polynomials. Of course, proving the N'th Fibonacci number is not an especially useful task, especially since Fibonacci numbers have a closed form. But you can use exactly the same basic technique, just with some extra polynomials and some more complicated equations, to encode arbitrary computations with an arbitrarily large number of steps.Now, if only there was a way to verify equations with polynomials that's much faster than checking each coefficient...Polynomial commitmentsAnd once again, it turns out that there is an answer: polynomial commitments. A polynomial commitment is best viewed as a special way to "hash" a polynomial, where the hash has the additional property that you can check equations between polynomials by checking equations between their hashes. Different polynomial commitment schemes have different properties in terms of exactly what kinds of equations you can check.Here are some common examples of things you can do with various polynomial commitment schemes (we use \(com(P)\) to mean "the commitment to the polynomial \(P\)"):Add them: given \(com(P)\), \(com(Q)\) and \(com(R)\) check if \(P + Q = R\) Multiply them: given \(com(P)\), \(com(Q)\) and \(com(R)\) check if \(P * Q = R\) Evaluate at a point: given \(com(P)\), \(w\), \(z\) and a supplemental proof (or "witness") \(Q\), verify that \(P(w) = z\) It's worth noting that these primitives can be constructed from each other. If you can add and multiply, then you can evaluate: to prove that \(P(w) = z\), you can construct \(Q(x) = \frac\), and the verifier can check if \(Q(x) * (x - w) + z \stackrel P(x)\). This works because if such a polynomial \(Q(x)\) exists, then \(P(x) - z = Q(x) * (x - w)\), which means that \(P(x) - z\) equals zero at \(w\) (as \(x - w\) equals zero at \(w\)) and so \(P(x)\) equals \(z\) at \(w\).And if you can evaluate, you can do all kinds of checks. This is because there is a mathematical theorem that says, approximately, that if some equation involving some polynomials holds true at a randomly selected coordinate, then it almost certainly holds true for the polynomials as a whole. So if all we have is a mechanism to prove evaluations, we can check eg. our equation \(P(x + 2) - P(x + 1) - P(x) = Z(x) * H(x)\) using an interactive game: As I alluded to earlier, we can make this non-interactive using the Fiat-Shamir heuristic: the prover can compute r themselves by setting r = hash(com(P), com(H)) (where hash is any cryptographic hash function; it does not need any special properties). The prover cannot "cheat" by picking P and H that "fit" at that particular r but not elsewhere, because they do not know r at the time that they are picking P and H!A quick recap so farZK-SNARKs are hard because the verifier needs to somehow check millions of steps in a computation, without doing a piece of work to check each individual step directly (as that would take too long). We get around this by encoding the computation into polynomials. A single polynomial can contain an unboundedly large amount of information, and a single polynomial expression (eg. \(P(x+2) - P(x+1) - P(x) = Z(x) * H(x)\)) can "stand in" for an unboundedly large number of equations between numbers. If you can verify the equation with polynomials, you are implicitly verifying all of the number equations (replace \(x\) with any actual x-coordinate) simultaneously. We use a special type of "hash" of a polynomial, called a polynomial commitment, to allow us to actually verify the equation between polynomials in a very short amount of time, even if the underlying polynomials are very large. So, how do these fancy polynomial hashes work?There are three major schemes that are widely used at the moment: bulletproofs, Kate and FRI.Here is a description of Kate commitments by Dankrad Feist: https://dankradfeist.de/ethereum/2020/06/16/kate-polynomial-commitments.html Here is a description of bulletproofs by the curve25519-dalek team: https://doc-internal.dalek.rs/bulletproofs/notes/inner_product_proof/index.html, and here is an explanation-in-pictures by myself: https://twitter.com/VitalikButerin/status/1371844878968176647 Here is a description of FRI by... myself: ../../../2017/11/22/starks_part_2.html Whoa, whoa, take it easy. Try to explain one of them simply, without shipping me off to even more scary linksTo be honest, they're not that simple. There's a reason why all this math did not really take off until 2015 or so.Please?In my opinion, the easiest one to understand fully is FRI (Kate is easier if you're willing to accept elliptic curve pairings as a "black box", but pairings are really complicated, so altogether I find FRI simpler).Here is how a simplified version of FRI works (the real protocol has many tricks and optimizations that are missing here for simplicity). Suppose that you have a polynomial \(P\) with degree \(< n\). The commitment to \(P\) is a Merkle root of a set of evaluations to \(P\) at some set of pre-selected coordinates (eg. \(\\), though this is not the most efficient choice). Now, we need to add something extra to prove that this set of evaluations actually is a degree \(< n\) polynomial.Let \(Q\) be the polynomial only containing the even coefficients of \(P\), and \(R\) be the polynomial only containing the odd coefficients of \(P\). So if \(P(x) = x^4 + 4x^3 + 6x^2 + 4x + 1\), then \(Q(x) = x^2 + 6x + 1\) and \(R(x) = 4x + 4\) (note that the degrees of the coefficients get "collapsed down" to the range \([0...\frac)\)).Notice that \(P(x) = Q(x^2) + x * R(x^2)\) (if this isn't immediately obvious to you, stop and think and look at the example above until it is).We ask the prover to provide Merkle roots for \(Q(x)\) and \(R(x)\). We then generate a random number \(r\) and ask the prover to provide a "random linear combination" \(S(x) = Q(x) + r * R(x)\).We pseudorandomly sample a large set of indices (using the already-provided Merkle roots as the seed for the randomness as before), and ask the prover to provide the Merkle branches for \(P\), \(Q\), \(R\) and \(S\) at these indices. At each of these provided coordinates, we check that:\(P(x)\) actually does equal \(Q(x^2) + x * R(x^2)\) \(S(x)\) actually does equal \(Q(x) + r * R(x)\) If we do enough checks, then we can be convinced that the "expected" values of \(S(x)\) are different from the "provided" values in at most, say, 1% of cases.Notice that \(Q\) and \(R\) both have degree \(< \frac\). Because \(S\) is a linear combination of \(Q\) and \(R\), \(S\) also has degree \(< \frac\). And this works in reverse: if we can prove \(S\) has degree \(< \frac\), then the fact that it's a randomly chosen combination prevents the prover from choosing malicious \(Q\) and \(R\) with hidden high-degree coefficients that "cancel out", so \(Q\) and \(R\) must both be degree \(< \frac\), and because \(P(x) = Q(x^2) + x * R(x^2)\), we know that \(P\) must have degree \(< n\).From here, we simply repeat the game with \(S\), progressively "reducing" the polynomial we care about to a lower and lower degree, until it's at a sufficiently low degree that we can check it directly. As in the previous examples, "Bob" here is an abstraction, useful for cryptographers to mentally reason about the protocol. In reality, Alice is generating the entire proof herself, and to prevent her from cheating we use Fiat-Shamir: we choose each randomly samples coordinate or r value based on the hash of the data generated in the proof up until that point.A full "FRI commitment" to \(P\) (in this simplified protocol) would consist of:The Merkle root of evaluations of \(P\) The Merkle roots of evaluations of \(Q\), \(R\), \(S_1\) The randomly selected branches of \(P\), \(Q\), \(R\), \(S_1\) to check \(S_1\) is correctly "reduced from" \(P\) The Merkle roots and randomly selected branches just as in steps (2) and (3) for successively lower-degree reductions \(S_2\) reduced from \(S_1\), \(S_3\) reduced from \(S_2\), all the way down to a low-degree \(S_k\) (this gets repeated \(\approx log_2(n)\) times in total) The full Merkle tree of the evaluations of \(S_k\) (so we can check it directly) Each step in the process can introduce a bit of "error", but if you add enough checks, then the total error will be low enough that you can prove that \(P(x)\) equals a degree \(< n\) polynomial in at least, say, 80% of positions. And this is sufficient for our use cases. If you want to cheat in a zk-SNARK, you would need to make a polynomial commitment for a fractional expression (eg. to "prove" the false claim that \(x^2 + 2x + 3\) evaluated at \(4\) equals \(5\), you would need to provide a polynomial commitment for \(\frac = x + 6 + \frac\)). The set of evaluations for such a fractional expression would differ from the evaluations for any real degree \(< n\) polynomial in so many positions that any attempt to make a FRI commitment to them would fail at some step.Also, you can check carefully that the total number and size of the objects in the FRI commitment is logarithmic in the degree, so for large polynomials, the commitment really is much smaller than the polynomial itself.To check equations between different polynomial commitments of this type (eg. check \(A(x) + B(x) = C(x)\) given FRI commitments to \(A\), \(B\) and \(C\)), simply randomly select many indices, ask the prover for Merkle branches at each of those indices for each polynomial, and verify that the equation actually holds true at each of those positions.The above description is a highly inefficient protocol; there is a whole host of algebraic tricks that can increase its efficiency by a factor of something like a hundred, and you need these tricks if you want a protocol that is actually viable for, say, use inside a blockchain transaction. In particular, for example, \(Q\) and \(R\) are not actually necessary, because if you choose your evaluation points very cleverly, you can reconstruct the evaluations of \(Q\) and \(R\) that you need directly from evaluations of \(P\). But the above description should be enough to convince you that a polynomial commitment is fundamentally possible.Finite fieldsIn the descriptions above, there was a hidden assumption: that each individual "evaluation" of a polynomial was small. But when we are dealing with polynomials that are big, this is clearly not true. If we take our example from above, \(628x^ + 318x^ + 530x^ + ... + 69x + 381\), that encodes 816 digits of tau, and evaluate it at \(x=1000\), you get.... an 816-digit number containing all of those digits of tau. And so there is one more thing that we need to add. In a real implementation, all of the arithmetic that we are doing here would not be done using "regular" arithmetic over real numbers. Instead, it would be done using modular arithmetic.We redefine all of our arithmetic operations as follows. We pick some prime "modulus" p. The % operator means "take the remainder of": \(15\ \%\ 7 = 1\), \(53\ \%\ 10 = 3\), etc (note that the answer is always non-negative, so for example \(-1\ \%\ 10 = 9\)). We redefine\(x + y \Rightarrow (x + y)\) % \(p\)\(x * y \Rightarrow (x * y)\) % \(p\)\(x^y \Rightarrow (x^y)\) % \(p\)\(x - y \Rightarrow (x - y)\) % \(p\)\(x / y \Rightarrow (x * y ^)\) % \(p\)The above rules are all self-consistent. For example, if \(p = 7\), then:\(5 + 3 = 1\) (as \(8\) % \(7 = 1\)) \(1 - 3 = 5\) (as \(-2\) % \(7 = 5\)) \(2 \cdot 5 = 3\) \(3 / 5 = 2\) (as (\(3 \cdot 5^5\)) % \(7 = 9375\) % \(7 = 2\)) More complex identities such as the distributive law also hold: \((2 + 4) \cdot 3\) and \(2 \cdot 3 + 4 \cdot 3\) both evaluate to \(4\). Even formulas like \((a^2 - b^2)\) = \((a - b) \cdot (a + b)\) are still true in this new kind of arithmetic.Division is the hardest part; we can't use regular division because we want the values to always remain integers, and regular division often gives non-integer results (as in the case of \(3/5\)). We get around this problem using Fermat's little theorem, which states that for any nonzero \(x < p\), it holds that \(x^\) % \(p = 1\). This implies that \(x^\) gives a number which, if multiplied by \(x\) one more time, gives \(1\), and so we can say that \(x^\) (which is an integer) equals \(\frac\). A somewhat more complicated but faster way to evaluate this modular division operator is the extended Euclidean algorithm, implemented in python here. Because of how the numbers "wrap around", modular arithmetic is sometimes called "clock math"With modular math we've created an entirely new system of arithmetic, and it's self-consistent in all the same ways traditional arithmetic is self-consistent. Hence, we can talk about all of the same kinds of structures over this field, including polynomials, that we talk about in "regular math". Cryptographers love working in modular math (or, more generally, "finite fields") because there is a bound on the size of a number that can arise as a result of any modular math calculation - no matter what you do, the values will not "escape" the set \(\\). Even evaluating a degree-1-million polynomial in a finite field will never give an answer outside that set.What's a slightly more useful example of a computation being converted into a set of polynomial equations?Let's say we want to prove that, for some polynomial \(P\), \(0 \le P(n) < 2^\), without revealing the exact value of \(P(n)\). This is a common use case in blockchain transactions, where you want to prove that a transaction leaves a balance non-negative without revealing what that balance is.We can construct a proof for this with the following polynomial equations (assuming for simplicity \(n = 64\)):\(P(0) = 0\) \(P(x+1) = P(x) * 2 + R(x)\) across the range \(\\) \(R(x) \in \\) across the range \(\\) The latter two statements can be restated as "pure" polynomial equations as follows (in this context \(Z(x) = (x - 0) * (x - 1) * ... * (x - 63)\)):\(P(x+1) - P(x) * 2 - R(x) = Z(x) * H_1(x)\) \(R(x) * (1 - R(x)) = Z(x) * H_2(x)\) (notice the clever trick: \(y * (1-y) = 0\) if and only if \(y \in \\)) The idea is that successive evaluations of \(P(i)\) build up the number bit-by-bit: if \(P(4) = 13\), then the sequence of evaluations going up to that point would be: \(\\). In binary, 1 is 1, 3 is 11, 6 is 110, 13 is 1101; notice how \(P(x+1) = P(x) * 2 + R(x)\) keeps adding one bit to the end as long as \(R(x)\) is zero or one. Any number within the range \(0 \le x < 2^\) can be built up over 64 steps in this way, any number outside that range cannot.PrivacyBut there is a problem: how do we know that the commitments to \(P(x)\) and \(R(x)\) don't "leak" information that allows us to uncover the exact value of \(P(64)\), which we are trying to keep hidden?There is some good news: these proofs are small proofs that can make statements about a large amount of data and computation. So in general, the proof will very often simply not be big enough to leak more than a little bit of information. But can we go from "only a little bit" to "zero"? Fortunately, we can.Here, one fairly general trick is to add some "fudge factors" into the polynomials. When we choose \(P\), add a small multiple of \(Z(x)\) into the polynomial (that is, set \(P'(x) = P(x) + Z(x) * E(x)\) for some random \(E(x)\)). This does not affect the correctness of the statement (in fact, \(P'\) evaluates to the same values as \(P\) on the coordinates that "the computation is happening in", so it's still a valid transcript), but it can add enough extra "noise" into the commitments to make any remaining information unrecoverable. Additionally, in the case of FRI, it's important to not sample random points that are within the domain that computation is happening in (in this case \(\\)).Can we have one more recap, please??The three most prominent types of polynomial commitments are FRI, Kate and bulletproofs. Kate is the simplest conceptually but depends on the really complicated "black box" of elliptic curve pairings. FRI is cool because it relies only on hashes; it works by successively reducing a polynomial to a lower and lower-degree polynomial and doing random sample checks with Merkle branches to prove equivalence at each step. To prevent the size of individual numbers from blowing up, instead of doing arithmetic and polynomials over the integers, we do everything over a finite field (usually integers modulo some prime p) Polynomial commitments lend themselves naturally to privacy preservation because the proof is already much smaller than the polynomial, so a polynomial commitment can't reveal more than a little bit of the information in the polynomial anyway. But we can add some randomness to the polynomials we're committing to to reduce the information revealed from "a little bit" to "zero". What research questions are still being worked on?Optimizing FRI: there are already quite a few optimizations involving carefully selected evaluation domains, "DEEP-FRI", and a whole host of other tricks to make FRI more efficient. Starkware and others are working on this. Better ways to encode computation into polynomials: figuring out the most efficient way to encode complicated computations involving hash functions, memory access and other features into polynomial equations is still a challenge. There has been great progress on this (eg. see PLOOKUP), but we still need more, especially if we want to encode general-purpose virtual machine execution into polynomials. Incrementally verifiable computation: it would be nice to be able to efficiently keep "extending" a proof while a computation continues. This is valuable in the "single-prover" case, but also in the "multi-prover" case, particularly a blockchain where a different participant creates each block. See Halo for some recent work on this. I wanna learn more!My materialsSTARKs: part 1, part 2, part 3 Specific protocols for encoding computation into polynomials: PLONK Some key mathematical optimizations I didn't talk about here: Fast Fourier transforms Other people's materialsStarkware's online course Dankrad Feist on Kate commitments Bulletproofs